Что такое среднее гармоническое число

Среднее гармоническое

Предлагаемая здесь программа, помимо расчета среднего гармонического, умеет еще и приводить исходные данные к стандартному виду, а так же упорядочивать их по возрастанию или убыванию.

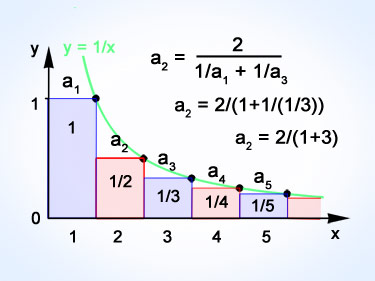
Рис.1. Гармонический ряд и среднее гармоническое

Среднее гармоническое от двух реже трех чисел используется в математике не менее двух с половиной тысяч лет (возможно более 4000 лет). Свойства средних гармонических, арифметических и геометрических величин для двух чисел были детально изучены еще пифагорейцами, поэтому они так же называются классическими пифагорейскими средними.

Свое название среднее гармоническое получило благодаря замечательному свойству гармонического ряда: каждый член ряда, начиная со второго, представляет собой среднее обратно-пропорциональное от двух соседних членов (рисунок). Это свойство гармонического ряда было известно еще во времена Аристотеля.
.

В свете современных представлений:

Среднее гармоническое значение множества положительных вещественных чисел определяется как результат деления количества этих чисел на сумму их обратных величин:

Среднее степенное значение s_d порядка (степени) d от множества заданных чисел a ₁ + a ₂ + …+ a _n определяется формулой:

Источник

Гармоническое Среднее

Что такое Гармоническое Среднее?

Гармоническое среднее – это разновидность среднего численного значения. Он рассчитывается путем деления количества наблюдений на обратную величину каждого числа в серии. Таким образом, гармоническое среднее является величиной, обратной среднему арифметическому обратных величин.

Среднее гармоническое значение 1, 4 и 4 равно:

Краткая справка

Обратное значение числа n равно 1 / n.

Основы гармонического среднего

Гармоническое среднее помогает найти мультипликативные отношения или отношения делителей между дробями, не беспокоясь об общих знаменателях. Гармонические средние часто используются для усреднения таких вещей, как скорости (например, средняя скорость движения при продолжительности нескольких поездок).

Средневзвешенное гармоническое среднее используется в финансах для усреднения мультипликаторов, таких как соотношение цены и прибыли, поскольку оно придает одинаковый вес каждой точке данных. Использование взвешенного среднего арифметического для усреднения этих соотношений даст больший вес высоким точкам данных, чем низким точкам данных, потому что соотношение цена / прибыль не нормализуется по цене, в то время как прибыль выравнивается.

Ключевые моменты

Сравнение среднего гармонического и среднего арифметического и среднего геометрического

Другие способы вычисления средних значений включают простое среднее арифметическое и среднее геометрическое. Среднее арифметическое – это сумма серии чисел, деленная на количество этой серии чисел. Если бы вас попросили найти среднее (арифметическое) среднее количество баллов за тест, вы просто сложите все баллы учащихся, а затем разделите эту сумму на количество учащихся. Например, если пять студентов сдали экзамен и их баллы составили 60%, 70%, 80%, 90% и 100%, средняя арифметическая оценка по классу будет 80%.

Среднее геометрическое среднее из набора продуктов, расчет которых обычно используется для определения результатов эффективности инвестиций или портфеля. Технически это определяется как «произведение корня n-й степени из n чисел». Среднее геометрическое должно использоваться при работе с процентами, которые выводятся из значений, в то время как стандартное среднее арифметическое работает с самими значениями.

Гармоническое среднее лучше всего использовать для таких дробей, как ставки или кратные.

Пример среднего гармонического

В качестве примера возьмем две фирмы. Один имеет рыночную капитализацию 100 миллиардов долларов и прибыль 4 миллиарда долларов (P / E 25), а другой – рыночную капитализацию 1 миллиард долларов и прибыль 4 миллиона долларов (P / E 250). В индексе, составленном из двух акций, с 10% инвестиций в первую и 90% во вторую, коэффициент P / E индекса равен:

Источник

Гармоническое число

В математике n-м гармоническим числом называется сумма обратных величин первых n последовательных чисел натурального ряда:

Гармонические числа являются частичными суммами гармонического ряда.

Изучение гармонических чисел началось в античности. Они имеют важное значение в различных областях теории чисел и теории алгоритмов и, в частности, тесно связаны с дзета-функцией Римана.

Содержание

Альтернативные определения

Дополнительные представления

Нижеследующие формулы могут быть использованы для вычисления гармонических чисел (в том числе и в точках отличных от точек натурального ряда):

Свойства

Значения от нецелого аргумента

Суммы, связанные с гармоническими числами

Теоретико-числовые свойства

Приложения

В 2002 году Lagarias доказал, [1] что гипотеза Римана о нулях дзета-функции Римана эквивалентна утверждению, что неравенство

верно при всех целых со строгим неравенством при 1″ border=»0″ />, где — сумма делителей числа .

См. также

Примечания

Полезное

Смотреть что такое «Гармоническое число» в других словарях:

Гармоническое среднее — число (у), обратное которому есть Арифметическое среднее чисел, обратных данным числам (а1, a2. an): … Большая советская энциклопедия

ГАРМОНИЧЕСКОЕ СРЕДНЕЕ — число (у), обратное к рому есть арифметич. среднее чисел, обратных данным числам (a1 a2. an) … Большой энциклопедический политехнический словарь

Число 666 — 666 шестьсот шестьдесят шесть 663 · 664 · 665 · 666 · 667 · 668 · 669 Факторизация: 2⋅32⋅37 Римская запись: DCLXVI Двоичное: 1010011010 Восьмеричное: 1232 Шестнадцатеричное: 29A … Википедия

Среднее гармоническое — Средним гармоническим нескольких положительных чисел называется число, обратное среднему арифметическому их обратных, то есть число Содержание 1 Свойства 2 Приложения и примеры … Википедия

666 (число) — 666 шестьсот шестьдесят шесть 663 · 664 · 665 · 666 · 667 · 668 · 669 Факторизация: Римская запись: DCLXVI Двоичное: 1010011010 Восьмеричное: 1232 Шестнадцатеричное: 29A … Википедия

Задача о джипе — (англ. Jeep problem, desert crossing problem, exploration problem) математическая задача, целью которой является максимизация пути, который можно преодолеть на джипе с полным баком топлива в труднопреодолимых условиях, к примеру, в… … Википедия

Биномиальный коэффициент — В математике биномиальные коэффициенты это коэффициенты в разложении бинома Ньютона по степеням x. Коэффициент при обозначается или и читается «биномиальный коэффициент из n по k» (или «це из n по k»): В … Википедия

Гипотеза Римана — Задачи тысячелетия Равенство классов P и NP Гипотеза Ходжа Гипотеза Пуанкаре Гипотеза Римана Квантовая теория Янга Миллса Существование и гладкость решений уравнений Навье Стокса Гипотеза Бёрча Свиннертон Дайера Гипотеза Римана о… … Википедия

Источник

Среднее гармоническое

Средним гармоническим нескольких положительных чисел называется число, обратное среднему арифметическому их обратных, то есть число

Содержание

Свойства

Приложения и примеры

В статистике среднее гармоническое применяется в случае, когда наблюдения, для которых требуется получить среднее арифметическое, заданы обратными значениями.

В формуле тонкой линзы удвоенное фокусное расстояние равно среднему гармоническому расстояния от линзы до предмета и расстояния от линзы до изображения. Подобным образом среднее гармоническое входит и в аналогичную формулу для сферического зеркала.

См. также

Примечания

Статистические показатели
Описательная статистика	Непрерывные данные Коэффициент сдвига Среднее (Арифметическое, Геометрическое, Гармоническое) · Медиана · Мода · Размах Вариация Ранг · Среднеквадратическое отклонение · Коэффициент вариации · Квантиль (Дециль, Процентиль/Перцентиль/Центиль) Моменты Математическое ожидание · Дисперсия · Асимметрия · Эксцесс Дискретные данные Частота · Таблица контингентности
Статистический вывод и проверка гипотез	Статистический вывод Доверительный интервал (Частотная вероятность) · Достоверный интервал (Байесовский вывод) · Статистическая значимость · Мета-анализ Планирование эксперимента Генеральная совокупность · Планирование выборки · Районированная выборка · Репликация · Группировка · Чувствительность и специфичность Объём выборки Статистическая мощность · Мера эффекта · Стандартная ошибка Общая оценка Байесовская оценка решения · Метод максимального правдоподобия · Метод моментов нахождения оценок · Оценка минимального расстояния · Оценка максимального интервала Статистические критерии Z-тест · t-критерий Стьюдента · Критерий Фишера · Критерий Пирсона (Хи-квадрат) · Критерий согласия Колмогорова · Тест Вальда · U-критерий Манна — Уитни · Критерий Уилкоксона · Критерий Краскела — Уоллиса · Критерий Кохрена · Критерий Лиллиефорса Анализ выживания Функция выживания · Оценка Каплана — Мейера · Логранк-тест · Интенсивность отказов · Пропорциональная модель опасностей
Корреляция	Коэффициент корреляции Пирсона · Ранг корреляций (Коэффициент Спирмана для ранга корреляций, Коэффициент тау Кендалла для ранга корреляций) · Переменная смешивания
Линейные модели	Основная линейная модель · Обобщённая линейная модель · Анализ вариаций · Ковариационный анализ
Регрессия	Линейная · Нелинейная · Непараметрическая регрессия · Полупараметрическая регрессия · Логистическая регрессия

Столбчатая диаграмма · Совмещённая диаграмма · Диаграмма управления · Лесная диаграмма · Гистограмма · Q-Q диаграмма · Диаграмма выполнения · Диаграмма разброса · Стебель-листья · Ящик с усами

Полезное

Смотреть что такое «Среднее гармоническое» в других словарях:

СРЕДНЕЕ ГАРМОНИЧЕСКОЕ — англ. mean, harmonic; нем. Mittel, harmonisches. Измерение центральной тенденции ряда мат. величин, исчисляемое произведением n числа величин и извлечением корня n степени из этого произведения. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии

среднее гармоническое — harmoninis vidurkis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. harmonic average; harmonic mean vok. harmonisches Mittel, n rus. среднее гармоническое, n… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

среднее гармоническое — harmoninis vidurkis statusas T sritis fizika atitikmenys: angl. harmonic average; harmonic mean vok. harmonisches Mittel, n rus. среднее гармоническое, n pranc. moyenne harmonique, f … Fizikos terminų žodynas

СРЕДНЕЕ, ГАРМОНИЧЕСКОЕ — Измерение центральной тенденции набора значений, представленное обратной величиной среднего арифметического обратных величин набора значений. Имеет ограниченное использование, преимущественно встречается при определении среднестатистической… … Толковый словарь по психологии

СРЕДНЕЕ ГАРМОНИЧЕСКОЕ — англ. mean, harmonic; нем. Mittel, harmonisches. Измерение центральной тенденции ряда мат. величин, исчисляемое произведением n числа величин и извлечением корня n степени из этого произведения … Толковый словарь по социологии

Среднее гармоническое взвешенное — набора вещественных чисел с вещественными весами определяется как В том случае, если все веса равны между собой, среднее гармоническое взвешенное равно среднему гармоническому. Существуют также взвешенные версии для других средних величин.… … Википедия

Среднее геометрическое взвешенное — набора вещественных чисел с вещественными весами определяется как В том случае, если все веса равны между собой, среднее геометрическое взвешенное равно среднему геометрическому. См. также Среднее геометрическое … Википедия

Среднее арифметическое взвешенное — набора вещественных чисел с вещественными весами определяется как Часто подразумевают, что сумма весов равна 1, тогда формула выглядит следующим образом: В том случае, если все веса равны между собой, среднее арифметическое взвешенное будет равно … Википедия

Среднее взвешенное — Среднее взвешенное общее название группы разновидностей среднего значения либо короткое название для любого из перечисленных: Среднее арифметическое взвешенное Среднее геометрическое взвешенное Среднее гармоническое взвешенное … Википедия

Источник

Термин «гармоническое» возникает в результате его использования применительно к типу рядов, включающих обратные значения, известных как гармонические ряды.

Формула среднего гармонического.

Среднее гармоническое (англ. ‘harmonic mean’) множества наблюдений \( X_1, X_2, \ldots, X_n \) есть

\(\large \dst
\overline X_H = n \Big/ \sum_^(1/X_i) \) (Формула 7)

Среднее гармоническое можно рассматривать как особый тип взвешенного среднего, в котором вес наблюдения обратно пропорционален его величине.

Концепцию лучше всего объяснить с помощью иллюстрации.

Пример расчета и пременения среднего гармонического.

Хорошо известный пример применения среднего гармонического возникает в инвестиционной стратегии, известной как усреднение издержек (англ. ‘cost averaging’), которая включает периодическое инвестирование фиксированной суммы денег.

Предположим, что инвестор покупает €1,000 ценных бумаг каждый месяц в течение \(n = 2\) месяцев. Цены на акции составляют €10 и €15 на две даты покупки.

Какова средняя цена акций?

В этом примере в 1-м месяце мы приобретаем €1,000 / €10 = 100 акций, а во 2-м месяце мы приобретаем €1,000 / €15 = 66.67 или 166.67 акций. Разделив общую сумму вложенных евро, €2,000, на общее количество приобретенных акций 166.67, мы получаем среднюю цену, уплаченную за акции, в размере €2,000 / 166.67 = €12.

Средняя цена фактически является средним гармоническим значением цен актива на даты покупки. По Формуле 7 средняя гармоническая цена составляет:

Значение €12 меньше среднеарифметической цены покупки акций:

Тем не менее, мы могли бы найти правильное значение €12, используя формулу средневзвешенного значения, где весовые коэффициенты, применяемые к ценам, равны долям акций, приобретенным по данной цене, от общего количества приобретенных акций.

В нашем примере расчет будет таким:

\( (100/166.67)\€10.00 + (66.67/166.67)\€15.00 = \€12 \)

Если бы мы инвестировали разные суммы денег на каждую дату, мы не могли бы использовать формулу гармонического среднего. Мы могли бы, однако, все еще использовать формулу взвешенного среднего значения способом, подобным только что описанному.

В приведенной иллюстрации средняя гармоническая цена действительно была меньше средней арифметической цены.

Источник