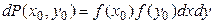Что такое среднее значение измерений в физике

Вычисление средних значений физических величин

Для характеристики случайной величины часто пользуются понятием среднего значения, которое определяется как:

(14)

Мерой отличия случайной величины x от среднего значения является дисперсия (среднеквадратичное отклонение), которая определяется как:

(15)

Раскрывая скобки и пользуясь определением средних величин можно получить простое выражение для расчета дисперсии:

(16)

Для расчета дисперсии биноминального распределения воспользуемся формулой (15) и результатом вычисления . Расчет можно провести аналогично :

Подстановка этой формулы в (15) приводит к значению дисперсии в биноминальном распределении:

Вычисление средних значений физических величин, зависящих от случайной величины x, проводится аналогично (14). Если известны вероятности различных состояний системы p_i, при этом требуется вычислить значения какой-либо физической величины u имеющей разные значения в каждом из состояний u_i=u(x_i). Вычисление среднего значения производится в соответствии с формулой:

(17)

В случае непрерывного распределения вероятности выражение для среднего значения величины u(x) определяется через функцию плотности вероятности f(x):

(15)

Распределение Гаусса

Распределение Гаусса достаточно часто встречается при описании реальных физических систем. Одной из основных задач, приводящих к получению распределения Гаусса, является задача о случайном блуждании частицы на плоскости. Если частица начинает блуждания из начала координат, то вероятность ее обнаружения через некоторое время в области площадью dxdy в окрестности точки (x₀, y₀), определяется в виде:

(16)

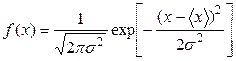
Здесь — среднее значение случайной величины x, — среднеквадратичное отклонение случайной величины x. График функции f(x) приведен на рис.2

Распределение Максвелла

Распределение Максвелла определяет функцию распределения частиц идеального газа по скоростям. По своему виду распределение Максвелла совпадает с распределением Гаусса, когда в качестве случайных величин выбираются проекции скорости молекул. Функция плотности вероятности для проекции скорости :

(17)

Поскольку компоненты скорости являются независимыми, то выражение (17) может быть перенесено и на компоненты скорости и . Общий вид графика функции (17) соответствует зависимости представленной на рис. 2.

В соответствии с (17) может быть получено распределение по модулю скорости:

(18)

График функции F(v) зависит от температуры

Распределение Максвелла F(v) может быть охарактеризовано несколькими характерными значениями скорости:

где — среднее значение модуля скорости, — наиболее вероятное значение скорости, — среднеквадратичное значение модуля скорости.

Вычисление среднего значения кинетической энергии молекул идеального газа, описываемых распределением Максвелла, может быть получено в виде:

(19)

Методика моделирования

Рассмотрим N частиц, идеального газа, имеющих одинаковую массу m, находящихся в закрытом сосуде. Каждая из частиц характеризуется вектором скорости или проекциями скоростей v_xi, v_yi, v_zi.

Предположим, что в начальный момент времени частицы идеального газа являются неподвижными. Поскольку частицы являются неподвижными, то кинетическая энергия равна нулю, а, следовательно, и температура, соответствующая такому состоянию, равна нулю (см. формулу (19)).

Если частицы газа взаимодействуют с поверхностью сосуда (посредством абсолютно упругого удара, т.е. условие идеальности газа не нарушается), находящегося при некоторой температуре T_сосуда, то температура газа постепенно увеличиваться до тех пор пока не будет достигнуто состояние термодинамического равновесия и температура газа не станет равной T_газа=T_сосуда. При каждом акте соударения со стенками сосуда происходит случайное изменение проекций импульса частиц газа. Предположим, что при каждом соударении (либо между собой, либо со стенками сосуда) изменяется только одна из проекций импульса на некоторую малую случайную величину Dp.

Таким образом, в системе реализуется случайное блуждание частиц из начального состояния (v_xi=0, v_yi=0, v_zi=0) с постоянным шагом Dp/m. При чем на каждом шаге изменяется только одна из проекций скорости. Так как температура газа имеет связь со средней кинетической энергией, то случайное блуждание в пространстве импульсов прекращается при достижении термодинамического равновесия со стенками сосуда (т.е. при равенстве температуры газа и температуры сосуда):

В результате расчета распределение частиц по скоростям будет соответствовать распределению Максвелла, записанному в формулах (17) и (18).

3. Практические задания

Выполнение работы с помощью программы LabStat.exe. Внешний вид программы представлен на рис.4. Для выполнения упражнений 1-3 необходимо выбрать соответствующую кнопку в диалоговом окне программы.

Рисунок 4Внешний вид программы LabStat.exe

Первые два упражнения являются ознакомительными, поскольку позволяют с помощью вычислительного эксперимента познакомиться с некоторыми закономерностями теории вероятностей, применяемыми в молекулярной физике.

В третьем упражнении предлагается проведение моделирования распределения частиц по проекции скорости и модулю скорости (распределение Максвелла).

Источник

Среднее арифметическое: физический смысл и визуализация

Переменная величина – атрибут (свойство) системы, меняющий свое числовое значение. Множество значений переменой величины может иметь вид:

Человек анализирует числовые данные такого рода и принимает решения. Знание температуры воздуха помогает правильно одеться. Курс валюты говорит покупать ее или продавать.

Когда значений одно или несколько, то никаких трудностей не возникает. Но когда значений десятки или сотни, то человеку сложно сразу понять, что означают полученные данные. На помощь приходят интегральные характеристики множеств значений и визуализация.

Одна из интегральных характеристик множества значений переменной величины – среднее арифметическое. Посмотрим на него с точки зрения статистики, физики (механики) и эстетики.

Среднее арифметическое двух чисел

Начнем с минимального набора чисел, для которых можно подсчитать среднее арифметическое. Вот два числа:

Их среднее арифметическое:

Физический смысл среднего арифметического

Изобразим два исходных числа и их среднее арифметическое на числовой оси:

Числа помечены черными кружками, а среднее арифметическое красным треугольником. Полученная конструкция – это весы. Для весов в равновесии правило рычага требует, чтобы моменты сил были равны. Весы не наклоняются ни в одну, ни в другую сторону, так как крутящий момент отсутствует.

В механике момент силы – это произведение силы F на расстояние l:

На плечи весов действует сила, создаваемая весом точек-«грузов». Обозначив расстояния от грузов до точки опоры l₁ и l₂, получим:

Точки-«грузы» отличаются только координатой на оси. Будем считать их вес одинаковым. Тогда:

Обозначив m координату точки опоры весов, получим:

Аналогично из формулы равенства моментов для произвольного количества N точек-«грузов» с одинаковым весом w выводится формула среднего арифметического. Равенство моментов для обоих плеч весов:

Координата опоры весов m:

Формула среднего арифметического дает координату точки опоры весов, находящихся в равновесии.

Визуальное восприятие равновесия

Равновесие в изобразительном искусстве играет важнейшую роль. Если при создании картины не достигнуто равновесие ее элементов, то произведение не будет законченным. В каждой картине художник создает равновесие различных визуальных сил.

Рудольф Арнхейм отмечает, что человеческое зрение способно обнаруживать малейшие отклонения от центра равновесия в изображении:

На приведенном примере слева круг находится в состоянии равновесия, а справа нет. Несмотря на то, что точка равновесия (центр квадрата) никак не отмечена на рисунке, человек с большой точностью может определить, находится ли круг в этой точке или нет.

Несмотря на то, что точка равновесия может быть не изображена, человек воспринимает ее как часть визуальной структуры:

Аналогично и среднее арифметическое: необязательно входит в набор чисел, но значимо для его восприятия и оценки.

Математическое ожидание случайной величины

Для случайной величины аналогом среднего арифметического служит математическое ожидание. Вероятность при этом можно считать весом точки-«груза». Формула равенства моментов с разными весами:

Теперь точка опоры весов в равновесии это μ:

Сумма всех вероятностей равна 1. Следовательно, и сумма весов равна 1. Тогда формула координаты точки весов в равновесии равна:

Это и есть формула математического ожидания.

Гистограмма

Гистограмма – это визуализация (геометрическое изображение) значений переменной величины с учетом вероятностей. Гистограмма показывает для выборки значений, какие из них появляются часто, какие реже, а какие совсем редко.

На гистограмме возможные значения откладываются по горизонтальной оси, а веса – по вертикальной. Диапазон значений по вертикали очевиден – от 0 до 1 (значения вероятности). По горизонтали диапазон должен включать ожидаемые значения переменной.

Гистограмма представляет собой простую картину (экземпляр изобразительного искусства). Зритель ожидает, что точка равновесия множества значений будет ровно посередине гистограммы:

Исходя из этого должен подбираться диапазон значений для горизонтальной оси гистограммы. Тогда сразу будет видно отклонение свойств выборки значений от ожидаемых:

Такого рода отклонение может быть вызвано выбросами. Выбросы – это значения, сильно отличающиеся от остальных. Благодаря правилу рычага, даже небольшое количество выбросов меняет точку равновесия и среднее арифметическое:

Дайте мне точку опоры, и я переверну Землю. Архимед

Источник

СРЕДНЕЕ ЗНАЧЕНИЕ

— то же, что математическое ожидание.

Смотреть что такое СРЕДНЕЕ ЗНАЧЕНИЕ в других словарях:

СРЕДНЕЕ ЗНАЧЕНИЕ

СРЕДНЕЕ ЗНАЧЕНИЕ (average) Статистический обобщенный показатель какой-либо величины. Среднее ряда чисел может быть взвешенным или невзвешенным. Невз. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ

(mean) См.: арифметическое среднее (arithmetic mean); геометрическое среднее (geometric mean); медиана (median).Бизнес. Толковый словарь. — М.: «ИНФРА-. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ

числовая характеристика группы чисел или функций. Для группы чисел наиб. употребительными С. з. являются: арифметическое среднее, гармоническое среднее. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ

1. snitt boxern blir i snitt tio år gammal—боксёры (порода собак) живут в среднем 10 лет

СРЕДНЕЕ ЗНАЧЕНИЕ

показатель, который принимает случайная переменная, равный средневзвешенной всех возможных значений переменной, в которой весами являются вероятности соответствующих событий. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ

сDurchschnittswert (m) Durchschnitt (m); Mittelwert (m); Mittel (n)

СРЕДНЕЕ ЗНАЧЕНИЕ

1) average value2) <math.> mean3) mean value4) population mean

СРЕДНЕЕ ЗНАЧЕНИЕ

MEAN) Среднее арифметическое или среднее ряда значений получается делением суммы этих значений на их число (п) в данном ряду.

СРЕДНЕЕ ЗНАЧЕНИЕ

(оценка текущей цены путем расчета среднего репрезентативной выборки совершенных сделок) average measures, average value

СРЕДНЕЕ ЗНАЧЕНИЕ

midvalue, medium, average value, mean value* * *mean

СРЕДНЕЕ ЗНАЧЕНИЕ

(медиана) midscore; average value

СРЕДНЕЕ ЗНАЧЕНИЕ

Durchschnitt, Durchschnittswert, Mittelwert

СРЕДНЕЕ ЗНАЧЕНИЕ

average value, mean value, mean

СРЕДНЕЕ ЗНАЧЕНИЕ

• průměrná hodnota• střední hodnota

СРЕДНЕЕ ЗНАЧЕНИЕ

measurement average, average, mean value

СРЕДНЕЕ ЗНАЧЕНИЕ

average value, mean value

СРЕДНЕЕ ЗНАЧЕНИЕ

moyenne, valeur moyenne

СРЕДНЕЕ ЗНАЧЕНИЕ

media, valore medio

СРЕДНЕЕ ЗНАЧЕНИЕ

СРЕДНЕЕ ЗНАЧЕНИЕ БЕЗРАЗМЕРНОГО АКУСТИЧЕСКОГО ИМПЕДАНСА

average acoustic impedance ratio

СРЕДНЕЕ ЗНАЧЕНИЕ ВЕЛИЧИНЫ

3.14 среднее значение величины: Средневзвешенное значение величины за определенный период времени (час, сутки). Источник: ГОСТ Р 8.733-2011: Государ. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ (ВЫБОРОЧНОЕ)

СРЕДНЕЕ ЗНАЧЕНИЕ ВЫБОРОЧНОЙ СОВОКУПНОСТИ

Среднее арифметическое, то есть сумма показателей, деленная на их количество.

СРЕДНЕЕ ЗНАЧЕНИЕ ГАРМОНИЧЕСКОЕ

гармоникалық орта мән

СРЕДНЕЕ ЗНАЧЕНИЕ ГЕОДЕЗИЧЕСКОЕ

геодезиялық орта мән

СРЕДНЕЕ ЗНАЧЕНИЕ ИЗБЫТОЧНОГО ДАВЛЕНИЯ В ПОДМАСОЧНОМ ПРОСТРАНСТВЕ ЛИЦЕВОЙ ЧАСТИ

3.8 среднее значение избыточного давления в подмасочном пространстве лицевой части: Среднеарифметическое значение величин избыточного давления воздух. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ ИЗМЕРЕНИЙ

Среднее значение измерений (mean value of measurements) — частное от деления алгебраической суммы значений измерений на число измерений.Примечание. Сре. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ ИНДУКТИВНОСТИ КАТУШКИ

40. Среднее значение индуктивности катушки Е. Mean value of inductance F. Valeur moyenne ďinductance Источник: ГОСТ 20718-75: Катушки индуктивности. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ ИНТЕРВАЛА

СРЕДНЕЕ ЗНАЧЕНИЕ МАССЫ ДОЗЫ

СРЕДНЕЕ ЗНАЧЕНИЕ МОДУЛЯ

mean value of modulus

СРЕДНЕЕ ЗНАЧЕНИЕ МОДУЛЯ КОЛЕБЛЮЩЕЙСЯ ВЕЛИЧИНЫ

23. Среднее значение модуля колеблющейся величины Среднее значение модуля Ндп. Средневыпрямленное значение (Поправка). Среднее арифметическое или ср. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ МОЩНОСТИ ФЛУКТУАЦИИ

mean fluctuation power

СРЕДНЕЕ ЗНАЧЕНИЕ НАБЛЮДАЕМОЙ

expectation value of an observable

СРЕДНЕЕ ЗНАЧЕНИЕ НАБЛЮДЕНИЙ

СРЕДНЕЕ ЗНАЧЕНИЕ НАПРЯЖЕНИЙ

СРЕДНЕЕ ЗНАЧЕНИЕ ОПЕРАТИВНОЙ ПРОДОЛЖИТЕЛЬНОСТИ КОРРЕКТИРУЮЩЕГО ТЕХНИЧЕСКОГО ОБСЛУЖИВАНИЯ

155 среднее значение оперативной продолжительности корректирующего технического обслуживания: Математическое ожидание оперативной продолжительности к. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ ПАРАМЕТРА ПОТОКА ОТКАЗОВ ЕДИНИЦЫ

61 среднее значение параметра потока отказов единицы [составной части единицы] (железнодорожного) тягового подвижного состава: Отношение числа отказо. смотреть

СРЕДНЕЕ ЗНАЧЕНИЕ ПАРАМЕТРА ШЕРОХОВАТОСТИ ПОВЕРХНОСТИ

Источник

Погрешности измерений, представление результатов эксперимента

п.1. Шкала измерительного прибора

Примеры шкал различных приборов:

Манометр – прибор для измерения давления, круговая шкала

Вольтметр – прибор для измерения напряжения, дуговая шкала

Индикатор громкости звука, линейная шкала

п.2. Цена деления

Пример определения цены деления:

Определим цену деления основной шкалы секундомера.
Два ближайших пронумерованных деления на основной шкале: a = 5 c
b = 10 c Между ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления.

Цена деления: \begin \triangle=\frac\\ \triangle=\frac<10-5><24+1>=\frac15=0,2\ c \end

п.3. Виды измерений

Физическую величину измеряют с помощью прибора

Измерение длины бруска линейкой

Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений

Определение площади столешницы при измеренной длине и ширине

п.4. Погрешность измерений, абсолютная и относительная погрешность

Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)

Определяется несовершенством методов и допущениями в методике.

Погрешность теории (модели)

Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.

Определяется субъективным фактором, ошибками экспериментатора.

Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.

В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:

Пример получения результатов прямых измерений с помощью линейки:

Второе измерение точнее, т.к. его относительная погрешность меньше.

п.5. Абсолютная погрешность серии измерений

Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).

Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.

Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.

Составим расчетную таблицу:

№ опыта	1	2	3	Сумма
Масса, г	99,8	101,2	100,3	301,3
Абсолютное отклонение, г	0,6	0,8	0,1	1,5

Сначала находим среднее значение всех измерений: \begin m_0=\frac<99,8+101,2+100,3><3>=\frac<301,3><3>\approx 100,4\ \text <г>\end Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности \(m_0\) и измерения. \begin \triangle_1=|100,4-99,8|=0,6\\ \triangle_2=|100,4-101,2|=0,8\\ \triangle_3=|100,4-100,3|=0,1 \end Находим среднее абсолютное отклонение: \begin \triangle_=\frac<0,6+0,8+0,1><3>=\frac<1,5><3>=0,5\ \text <(г)>\end Мы видим, что полученное значение \(\triangle_\) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: \begin \triangle m=max\left\<\triangle_; d\right\>=max\left\<0,5; 0,05\right\>\ \text <(г)>\end Записываем результат: \begin m=m_0\pm\triangle m\\ m=(100,4\pm 0,5)\ \text <(г)>\end Относительная погрешность (с двумя значащими цифрами): \begin \delta_m=\frac<0,5><100,4>\cdot 100\text<%>\approx 0,050\text <%>\end

п.6. Представление результатов эксперимента

Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.

Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.

п.7. Задачи

Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?

Составим таблицу для расчета цены деления:

№ мензурки	a, мл	b, мл	n	\(\triangle=\frac\), мл
1	20	40	4	\(\frac<40-20><4+1>=4\)
2	100	200	4	\(\frac<200-100><4+1>=20\)
3	15	30	4	\(\frac<30-15><4+1>=3\)
4	200	400	4	\(\frac<400-200><4+1>=40\)

Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):

№ мензурки	Объем \(V_0\), мл	Абсолютная погрешность \(\triangle V=\frac<\triangle><2>\), мл	Относительная погрешность \(\delta_V=\frac<\triangle V>\cdot 100\text<%>\)
1	68	2	3,0%
2	280	10	3,6%
3	27	1,5	5,6%
4	480	20	4,2%

Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.

Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка

Мерой точности является относительная погрешность измерений. Получаем: \begin \delta_1=\frac<0,1><4,0>\cdot 100\text<%>=2,5\text<%>\\ \delta_2=\frac<0,03><4,0>\cdot 100\text<%>=0,75\text <%>\end Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: \(\delta_2\lt \delta_1\), второе измерение точней.

Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.

Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.

Источник