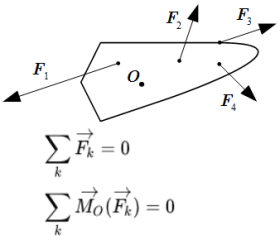
Что такое статика в технической механике

Техническая механика

Теоретическая механика

Статика

Статика — часть теоретической механики, изучающая условия, при которых тело находится в равновесии. При этом равновесием считается такое состояние тела, когда оно находится в покое (т. е. без движения) или движется прямолинейно и равномерно (т. е. с постоянной скоростью) .

Основные понятия и определения статики

В статике и теоретической механике при решении задач многие тела рассматриваются, как материальные точки, т. е. их размерами пренебрегают. Это позволяет значительно упростить расчеты при минимальной погрешности, вызываемой подобными условностями. Например, в астрономии, звезды рассматриваются, как материальные точки, несмотря на то, что они имеют колоссальные (по нашим меркам) размеры. При этом перемещение звезд в пространстве может быть рассчитано с высокой степенью точности.

Следует отметить, что одни и те же тела при решении задач технической механики (в зависимости от постановки задачи) могут рассматриваться либо, как материальная точка, либо, как тело, размеры которого необходимо учитывать. Всякое тело можно считать взаимосвязанной системой (совокупностью) материальных точек. При этом абсолютно твердое тело представляет собой неизменяемую систему материальных точек.

Статика при решении задач условия равновесия тел или материальных точек оперирует понятиями свободных и несвободных тел.

Источник

Статика – раздел теоретической механики

Определение и роль статики в теоретической механике

Основной задачей статики является установление законов преобразования системы сил в эквивалентные системы. Методы статики применяются не только при изучении тел, находящихся в равновесии, но и в динамике твердого тела, при преобразовании сил в более простые эквивалентные системы.

Под состоянием равновесия, в статике, понимается состояние, при котором все части механической системы покоятся относительно некоторой инерциальной системы координат. Одним из базовых объектов статики являются силы и точки их приложения.

Понятие силы

Единицей измерения силы является один Ньютон:
.
В технике широко используется килоньютон:
.

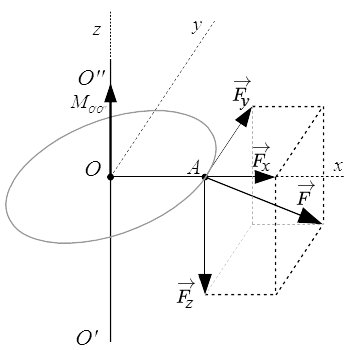
Как следует из определения, сила – это векторная величина, которая, в трехмерном пространстве, имеет три проекции на оси координат. Также задать силу можно с помощью абсолютной величины (модуля) и направления. Для материальной точки, сила приложена к самой точке. Но если мы рассматриваем твердое тело, то кроме вектора силы нам нужно еще указать и точку ее приложения. Таким образом, действие силы на твердое тело характеризуется вектором силы и точкой ее приложения. Если выбрать систему отсчета, то действие силы на твердое тело определяется двумя векторами. Это вектор силы, и вектор, проведенный из начала системы отсчета в точку приложения силы.

Система сил, действующих на тело – это совокупность векторов сил, приложенных к телу, и точек их приложения.
Эквивалентные системы сил Две системы сил являются эквивалентными, если законы движения любых точек твердого тела совпадают при действии любой из этих систем.
Эквивалентное преобразование системы сил – это переход от одной системы сил к эквивалентной ей системе.
Система взаимно уравновешивающихся сил – это система сил, не меняющая уравнений движения или уравнений равновесия твердого тела. То есть это система, эквивалентная отсутствию сил.
Равнодействующая – это одна сила, действие которой эквивалентно действию данной системы сил.

Закрепленные, скользящие и свободные векторы

Поскольку действие силы на твердое тело определяется двумя векторами, то часто под силой подразумевают множество, состоящее из двух векторов – вектора силы, и вектора точки ее приложения относительно выбранной системы координат. Такие множества подразделяются на три класса, для которых вводят специальные термины.

Закрепленный вектор – это множество, состоящее из образующего вектора и точки его приложения. Два закрепленных вектора считаются равными только в том случае, если равны их образующие векторы и совпадают точки приложения. Закрепленный вектор также называют связанным или фиксированным вектором.
Скользящий вектор – это множество, состоящее из образующего вектора и точки его приложения, обладающее тем свойством, что точку приложения можно перемещать вдоль прямой, параллельно образующему вектору. То есть два скользящих вектора считаются равными, если равны образующие векторы и точки их приложения расположены на одной прямой, параллельной образующему вектору.
Свободный вектор – это множество, состоящее из образующего вектора и точки его приложения. Два свободных вектора считаются равными, если равны образующие векторы, не зависимо от точек приложения.
Линия действия силы – это прямая, проведенная через точку приложения силы параллельно ее направлению.

Если мы рассматриваем упругое тело, то сила – это закрепленный вектор. Деформации зависят не только от величин и направлений сил, но и от точек их приложения. Если мы рассматриваем движение или равновесие абсолютно твердого тела, то действующая сила является скользящим вектором. Перемещение ее точки приложения вдоль линии ее действия не меняет уравнений движения или уравнений равновесия. Угловая скорость вращения абсолютно твердого тела является свободным вектором. Она характеризует движение в целом, и ее значение одинаково во всех точках тела.

С математической точки зрения, статика – это алгебра скользящих векторов.

Проекции силы на оси координат

Сила в трехмерном пространстве

Сила на плоскости

Аксиомы статики

Часть аксиом являются основными законами механики. Другая часть относится к законам преобразования сил, действующих на абсолютно твердое тело, и применяется только к задачам теоретической механики. По своей сути, они выражают собой тот факт, что действие силы на тело является скользящим вектором.

1. Аксиома инерции (закон инерции Галилея)
Существуют такие системы отсчета, в которых любая материальная точка, не взаимодействующая с другими телами и точками, движется прямолинейно и равномерно. В частности, если тело покоилось в определенный момент времени, то оно будет покоиться и в последующие моменты.

Такие системы отсчета называются инерциальными. В механике, если это особо не оговорено, под системой отсчета подразумевается именно инерциальная система отсчета. Аксиому инерции иногда формулируют так.

1′. Аксиома инерции
В инерциальной системе отсчета, под действием взаимно уравновешивающихся сил, материальная точка находится в состоянии покоя или движется прямолинейно и равномерно, а первоначально покоившееся тело продолжает покоиться и в последующие моменты времени.

2. Аксиома равновесия двух сил
Две силы, приложенные к абсолютно твердому телу, являются уравновешенными тогда и только тогда, когда они равны по модулю, направлены в противоположные стороны и их линии действия совпадают.

3. Аксиома присоединения и исключения уравновешивающихся сил
Кинематическое состояние твердого тела не изменится, если к действующей на него системе сил прибавить или отнять уравновешенную систему сил.

То есть, прибавляя или исключая уравновешенную систему сил, мы получаем эквивалентную систему сил.

Следствие аксиом 2 и 3
Действие силы на твердое тело не изменится, если точку приложения силы перенести вдоль ее линии действия. То есть сила, приложенная к твердому телу, является скользящим вектором. Доказательство

4. Аксиома параллелограмма сил
Две силы, приложенные к телу в одной точке, можно заменить их равнодействующей силой, равной векторной сумме этих сил и приложенной к той же точке.
Верно и обратное. Любую силу можно разложить на две (и более) силы по правилу векторной суммы (по правилу параллелограмма), приложенных в той же точке, что и исходная сила.

Сложение сил по правилу параллелограмма

5. Аксиома равенства действия и противодействия (3-й закон Ньютона)
Всякому действию соответствует равное и противоположно направленное противодействие.

То есть если мы возьмем все силы, действующие на тело 2 со стороны тела 1, и объединим их с силами, действующими на тело 1 со стороны тела 2, то получим уравновешенную систему сил.

6. Принцип отвердевания
Если деформируемое тело находится в равновесии, то его равновесие не нарушится, если тело считать абсолютно твердым.

Система сходящихся сил

Таким образом, проекции равнодействующей системы сходящихся сил на координатные оси равны алгебраическим суммам проекций этих сил на оси координат:
;
.

Условия равновесия системы сходящихся сил
Если тело или система тел, на которые действует сходящаяся система сил, находится в покое, то равнодействующая этих сил равна нулю:
.
Это дает три уравнения равновесия:
.

Теорема о трех непараллельных силах
Если твердое тело находится в равновесии под действием трех сил, линии действия двух из которых пересекаются в одной точке, то все силы лежат в одной плоскости и являются сходящимися.

Следствие
Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то эти силы являются сходящимися.

Параллельные силы

Ранее мы отмечали, что система сходящихся сил имеет равнодействующую. То есть такую систему можно заменить одной силой. Приведем еще важные примеры систем сил, имеющих равнодействующую.

Две силы одного направления

Две противоположно направленные силы

Момент силы относительно точки

Определение

Геометрическая интерпретация

Компоненты момента силы в декартовой системе координат

Свойства момента силы относительно центра

Если точку приложения силы переместить вдоль линии, проходящей через вектор силы, то момент, при таком перемещении, не изменится.
Доказательство

Момент от векторной суммы сил, приложенных к одной точке тела, равен векторной сумме моментов от каждой из сил, приложенных к этой же точке:
.
Доказательство

То же самое относится и к силам, чьи линии продолжения пересекаются в одной точке.

Если векторная сумма сил равна нулю:
,
то сумма моментов от этих сил не зависит от положения центра, относительно которого вычисляются моменты:
.
Доказательство

Теорема Вариньона о моменте равнодействующей
Если данная система сил имеет равнодействующую, то момент равнодействующей относительно любой точки равен векторной сумме моментов сил системы относительно той же точки.

Пара сил

Теорема о независимости выбора центра при вычислении момента пары
Векторная сумма моментов сил, составляющих пару, не зависит от выбора точки, относительно которой вычисляются моменты.
Теорема об эквивалентности пар
Две пары, имеющие равные векторы моментов, эквивалентны. То есть у пары можно менять модуль силы и длину плеча, оставляя неизменным ее момент.
Теорема о возможности перемещения пары
Пару сил можно переносить в любом направлении. Другими словами, если пару сил переместить параллельным переносом в любое положение, то она будет эквивалентна исходной паре.
Теорема о сложении нескольких пар
Система нескольких пар сил эквивалентна одной паре, вектор момента которой равен векторной сумме моментов исходных пар.
Условие равновесия пар
Система, состоящая только из нескольких пар, является уравновешенной, если векторная сумма моментов пар равна нулю:
.

Момент силы относительно оси

Часто встречаются случаи, когда нам нужно знать не все компоненты момента силы относительно выбранной точки, а только проекцию момента на выбранное направление.

Свойства момента силы относительно оси

Момент относительно оси от силы, линия действия которой проходит через эту ось, равен нулю.
Доказательство

Момент относительно оси от силы, параллельной этой оси равен нулю.
Доказательство

Вычисление момента силы относительно оси

Условия равновесия

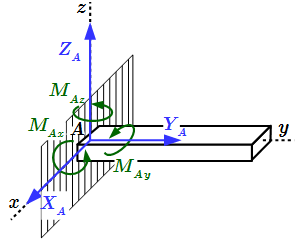
Главный вектор и главный момент

Подчеркнем, что величина главного момента зависит от выбора центра, относительно которого вычисляются моменты.

Пространственная система сил

Основная форма условий равновесия

Это основная форма условий равновесия. Точка C может, как принадлежать телу, так и находится за его пределами. Обычно центр C выбирают так, чтобы сделать вычисления более простыми. Спроектировав каждое из этих векторных уравнений на три направления, получим шесть уравнений, из которых можно определить шесть неизвестных величин.

Вторая форма условий равновесия

Третья форма условий равновесия

Плоская система сил

Условия равновесия плоского тела

Основная форма условий равновесия
;
;
.

Вторая форма условий равновесия
;
;
.

Третья форма условий равновесия
;
;
;
.

Связи и их реакции

Определения и свойства

Принцип освобождаемости
Всякое несвободное тело можно рассматривать как свободное, если действие связей заменить их реакциями, приложенными к телу.

Основные типы связей и их реакции

Плоские и пространственные задачи

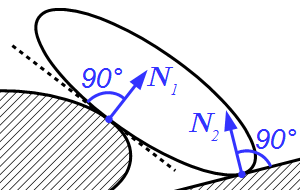
Две гладкие не острые поверхности. Через точку соприкосновения проводим касательную плоскость к этим поверхностям. Реакция является силой, направленной перпендикулярно этой плоскости, то есть, направлена по нормали к обеим поверхностям в точке их соприкосновения.

Одна из гладких поверхностей является острием. Реакция является силой, направленной вдоль нормали не острой поверхности в точке соприкосновения.

Две шероховатые поверхности. То же самое, что и для гладких поверхностей, только в точке соприкосновения добавляем силу трения, лежащую в плоскости касания.

Невесомая нить и стержень. Реакция направлена вдоль нити или стержня. При этом на нить всегда действует сила растяжения. На стержень может действовать как растягивающая, так и сжимающая сила.

Плоские задачи

Следующие связи применяют только в плоских задачах.

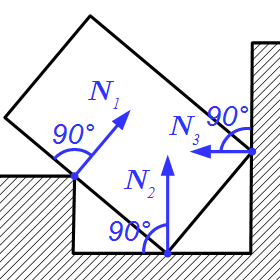
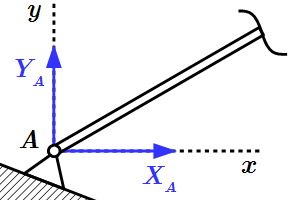
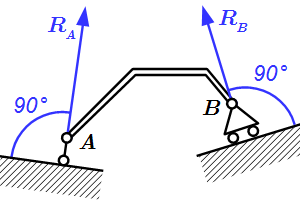
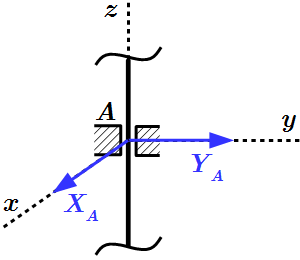
Неподвижный шарнир. Реакция является силой, проходящей через ось шарнира. Обычно ее раскладывают на две составляющие параллельно осям координат.

Подвижный шарнир, или опора на катках. Реакция является силой, которая проходит через ось шарнира перпендикулярно опорной поверхности.

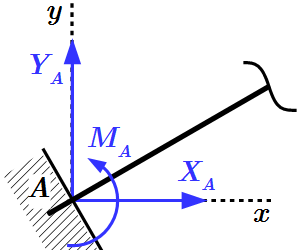
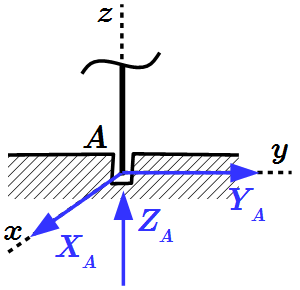
Заделка. Реакция состоит из силы, проходящей через точку соединения и момента относительно оси, проходящей через точку соединения перпендикулярно плоскости фигуры. Силу обычно раскладывают на две составляющие параллельно осям координат.

Пространственные задачи

Цилиндрический шарнир или петля. Реакция является силой, проходящей через ось шарнира, перпендикулярно направлению оси. Обычно ее раскладывают на две составляющие параллельно осям координат.

Сферический подшипник или подпятник. Реакция является силой, проходящей через центр подшипника. Обычно ее раскладывают на три составляющие параллельно осям координат.

Заделка. Реакция состоит из силы, проходящей через точку соединения и момента относительно этой точки. Силу и момент обычно раскладывают на три составляющие параллельно осям координат.

Силы трения

Трение скольжения

Сила трения скольжения – это сила трения, приложенная к точкам соприкосновения движущихся тел и параллельная плоскости их соприкосновения. То есть это сила, препятствующая скольжению одного тела по поверхности другого. При расчетах, под силой трения скольжения понимают равнодействующую всех сил трения, возникающих в точках соприкосновения тел.

Закон Амонта – Кулона
Сила трения скольжения направлена параллельно плоскости соприкосновения тел в сторону, противоположную их движению, которое возникло бы при отсутствии трения. Она не зависит от площади соприкосновения поверхностей, а зависит от силы давления N одной поверхности на другую, перпендикулярную плоскости соприкосновения тел:
.

Трение сцепления

Сила трения сцепления – это сила трения скольжения, когда относительное перемещение соприкасающихся тел отсутствует.
Предельная сила трения – это максимальное значение силы трения сцепления.
Предельное равновесие – это состояние равновесия, при котором значение силы трения сцепления равно ее максимальному значению.

Заклинивание механизма – это явление в механике, при котором система остается в состоянии покоя при любом, сколь угодно большом увеличении модуля внешней силы.

Условие возникновения движения при наличии трения
Для того чтобы тело начало движение, необходимо и достаточно, чтобы равнодействующая внешних сил находилась вне конуса трения.

Трение качения

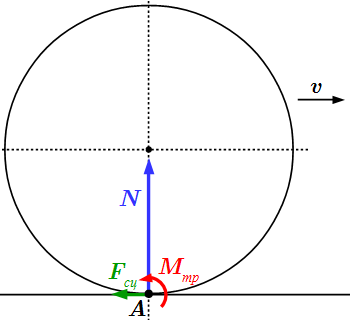
Расчетная схема трения качения.

Центр тяжести тела

Центр тяжести в пространстве

Если бы мы находили равнодействующую сил тяжести, выполняя эквивалентные преобразования сил, то мы бы нашли только линию действия равнодействующей. Далее, если повернуть тело на некоторый угол, то можно найти другую линию действия равнодействующей. При этом все, подобным образом построенные линии, пересекаются в одной точке, которая и является центром тяжести тела.

Центр тяжести твердого тела – это точка, связанная с телом, через которую проходит линия действия равнодействующей сил тяжести частиц тела, при любом положении тела в пространстве.
Вес тела – это абсолютное значение равнодействующей сил тяжести частиц, составляющих тело.

В случае, когда силы имеют другое происхождение, но также имеют одинаковое направление, то мы имеем дело с системой параллельных сил. В этом случае, точка C называется центром параллельных сил.

Центр тяжести плоской фигуры

Однородная фигура

В рассматриваемом нами случае, статические моменты относительно осей x, y определяются по формулам:
.
Статические моменты широко используются при расчете конструкций. Для стандартных профилей, их значения указываются в соответствующих справочниках.

Центры тяжести простейших фигур

Теоремы, применяемые при расчете центра тяжести

Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.

Если однородное тело имеет плоскость симметрии, то его центр тяжести находится в этой плоскости.

Распределенная нагрузка

Силу тяжести протяженных тел, на схемах, изображают в виде эпюр. Также встречаются подобные силе тяжести параллельные силы, приложенные не в определенных точках тела, а непрерывно распределенные по его поверхности или объему. Такие силы называют распределенными силами или распределенными нагрузками.

Приведение системы сил к центру

Теорема о параллельном переносе силы (лемма Пуансо)
Сила, действующая на данное тело, эквивалентна силе, полученной параллельным переносом исходной силы в любую точку тела и паре сил с моментом, равным моменту исходной силы относительно новой точки ее приложения.

Статические инварианты

Итак, статическими инвариантами являются следующие величины:
– квадрат модуля главного вектора;
– скалярное произведение главного вектора на главный момент. Инвариантами также являются функции от инвариантов. Например, проекция главного момента на направление главного вектора является инвариантом:
.

Динама

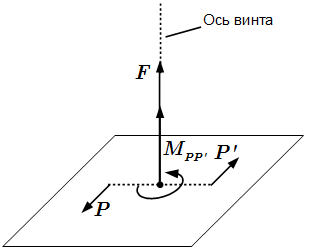
Динама – одна из простейших систем сил.

Из (П1) мы находим, что минимальное значение модуля момента равно модулю его проекции на направление главного вектора:
.

Центральная ось системы сил

Центральная ось системы сил – это прямая, обладающая тем свойством, что при приведении системы сил к любой из ее точек, система сил является динамой. При этом главный вектор и главный момент динамы параллельны этой прямой, а главный момент имеет наименьшее по модулю значение.

Приведение системы сил к простейшему виду

Пара сил

Равнодействующая сила

Динама

Использованная литература:
А. А. Яблонский, В.М. Никифорова. Курс теоретической механики, часть 1, статика, кинематика. Москва, «Высшая школа», 1966.
С. М. Тарг, Краткий курс теоретической механики, «Высшая школа», 2010.

Источник

Тема 1.1. Основные понятия и аксиомы статики

§1. Элементы векторной алгебры

В теоретической механике рассматриваются такие векторные величины как сила, моменты силы относительно точки и оси, момент пары сил, скорость, ускорение и другие.

1. Понятие вектора.

Операции над векторами. Вектора можно складывать и умножать на число.

— сумма двух векторов есть вектор

— существует нулевой вектор

Рис.1. Сложение векторов

В математике все вектора являются свободными, их можно переносить параллельно самим себе.

В сумме двух векторов (рис.1,а) начало второго вектора можно поместить в конец первого вектора, тогда сумму двух векторов можно представить как вектор, имеющий начало в начале первого вектора, а конец в конце второго вектора. Применяя это правило для суммы нескольких векторов (рис.1,б) получаем, что суммой нескольких векторов является вектор замыкающий ломаную линию, состоящую из слагаемых векторов.

Операции над векторами подчиняются следующим законам (см. рис.2):

Рис.2. Операции над векторами

2. Проекцией вектора на ось

Проекцией вектора на ось называется скалярная величина, которая определяется отрезком, отсекаемым перпендикулярами, опущенными из начала и конца вектора на эту ось. Проекция вектора считается положительной (+), если направление ее совпадает с положительным направлением оси, и отрицательной (-), если проекция направлена в противоположную сторону (см. рис.3).

Рис.3. Проекция вектора на ось

§2. Основные понятия статики

Статикой называется раздел механики, в котором излагается общее учение о силах и изучается условия равновесия материальных тел, находящихся под действием сил.

Твердое тело. В статике и вообще в теоретической механике все тела считаются абсолютно твердыми. То есть предполагается, что эти тела не де­формируются, не изменяют свою форму и объем, какое бы действие на них не было оказано. Материальной точкой будет называться абсолютно твердое тело, размерами которого можно пренебречь.

Под равновесием будем понимать состояния покоя тела по отношению к другим материальным телам.

1. Величина, являющаяся количественной мерой механического взаимодействия материальных тел, называется в механике силой.

В Международной системе единиц (СИ) силу измеряют в ньютонах (Н), килоньютонах (кН). Сила является величиной векторной.

Ее действие на тело опре­деляется:

1) численной величиной или модулем силы

2) направле­нием силы

3) точкой приложения силы (рис.4).

Рис.4. Сила, приложенная к телу

Силу, как и другие векторные величины, изображают в виде направленного отрезка со стрелкой на конце, указывающей его направление.

Прямая DE, вдоль которой направлена сила, называется линией действия силы.

Понятия «линия действия» и «направление» близки, но не тождественны. Очевидно, что по линии действия можно определить направление с точностью до противоположного. Аналогично связаны понятия «модуль» и «величина» для вектора.

2. Совокупность сил, действующих на какое-нибудь твердое тело, будем называть системой сил. Предполагается, что действие силы на тело не изменится, если ее перене­сти по линии действия в любую точку тела (конечно – твердого тела). Поэтому вектор силы называют скользящим вектором. Если силу перенести в точку, не расположенную на этой линии, действие ее на тело будет совсем другим.

3. Тело, не скрепленное с другими телами, которому из данного положения можно сообщить любое перемещение в пространстве, на­зывается свободным.

4. Если одну систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом состоя­ния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными.

Например, если системы сил, изображенных на рис. 5, а и рис. 5, б, уравновешены, то эти две системы сил будут эквивалентны друг другу.

Рис 5. Система сил:

а – заданная система сил; б – эквивалентная система сил

5. Система сил, под действием которой свободное твердое тело может находиться в покое, называется уравновешенной или экви­валентной нулю.

7. Сила, равная равнодействующей по модулю, прямо противополож­ная ей по направлению и действующая вдоль той же прямой, назы­вается уравновешивающей силой.

8. Силы, действующие на твердое тело, можно разделить на внешние и внутренние. Внешними называются силы, действующие на частицы данного тела со стороны других материальных тел. Внутренними называются силы, с которыми частицы данного тела действуют друг на друга.

9. Сила, приложенная к телу в какой-нибудь одной его точке, называется сосредоточенной.

Силы, действующие на все точки дан­ного объема или данной части поверхности тела, называются распре­деленными.

Понятие о сосредоточенной силе является условным, так как практически приложить силу к телу в одной точке нельзя. Силы, которые мы в механике рассматриваем как сосредоточенные, пред­ставляют собою по существу равнодействующие некоторых систем распределенных сил.

В частности, обычно рассматриваемая в механике сила тяжести, действующая на данное твердое тело, представляет собою равно­действующую сил тяжести его частиц. Линия действия этой равно­действующей проходит через точку, называемую центром тяжести тела.

§3. Аксиомы статики

Все теоремы и уравнения статики выво­дятся из нескольких исходных положений, принимаемых без матема­тических доказательств и называемых аксиомами или принципами статики. Аксиомы статики представляют собою результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой. Часть из этих аксиом является следствиями основных законов механики, с которыми мы познакомимся в динамике.

Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F₁ = F₂) и направлены вдоль одной прямой в противоположные стороны (рис. 6).

Рис.6. Система сил, находящаяся в равновесии

Аксиома 1 определяет простейшую уравновешенную систему сил, так как опыт показывает, что свободное тело, на которое действует только одна сила, находиться в равнове­сии не может.

Аксиома 2. Действие данной си­стемы, сил на абсолютно твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил.

Эта аксиома устанавливает, что две системы сил, отличающиеся на уравнове­шенную систему, эквивалентны друг другу.

Следствие из 1-й и 2-й аксиом. Действие силы на абсо­лютно твердое тело не изменится, если перенести точку при­ложения силы вдоль ее линии действия в любую другую точку тела.

Рис.7. Система сил

В самом деле, пусть на твердое тело действует приложенная в точке А сила (рис.7). Возьмем на линии действия этой силы произвольную точку В и приложим к ней две уравновешенные силы

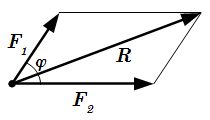
Аксиома 3 (аксиома параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю па­раллелограмма, построенного на этих силах, как на сторонах.

Рис.8. Равнодействующая двух сил

Следовательно, аксиому 3 можно еще формулировать так: две силы, приложенные к телу в одной точке, имеют равнодействую­щую, равную геометрической (векторной) сумме этих сил и прило­женную в той же точке.

Аксиома 4 (принцип противодействия). При всяком действии одного материального тела на другое имеет место такое же по величине, но проти­воположное по направлению противодействие.

(рис. 9). Однако силы и не образуют урав­новешенной системы сил, так как они приложены к разным телам. Эта аксиома соответствует третьему закону Ньютона: действие всегда равно и противоположно противодействию. При этом необходимо помнить, что в аксиоме 4 рассматривается случай, когда силы приложены к разным телам и в этом случае система сил не является уравновешенной в отличие от случая действия сил в аксиоме 2.

Рис.9. Противодействие

Рис. 10. Опирание балки на опоры:

а – схема загружения балки; б – силы действия балки на

опоры и противодействия со стороны опор на балку

Аксиома 5 (принцип отвердевания). Равновесие изме­няемого (деформируемого) тела, находящегося под действием дан­ной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твердым). Из принципа отвердения следует, что условия, необходимые и достаточные для равновесия абсолютно твердого тела, необходимы, но не достаточны для равновесия деформируемого тела, по форме и размерам тождественного с данным.

Высказанное в этой аксиоме утверждение очевидно. Например, ясно, что равновесие цепи не нарушится, если ее звенья считать сва­ренными друг с другом и т. д.

Аксиома 6 (аксиома связей). Всякое несвободное тело можно рассматривать как свободное, если механическое действие связей заменить реакциями этих связей (пояснения к этой аксиоме в следующем параграфе).

Приведенные принципы и аксиомы положены в основу методов решения задач статики. Все они широко используются в инженерных расчетах.

Видео-урок «Аксиомы статики»

§4. Связи и их реакции

По определению, тело, которое не скреплено с другими телами и может совершать из данного положе­ния любые перемещения в пространстве, называется свободным (например, воздушный шар в воздухе). Тело, перемещениям которого в пространстве препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным. Все то, что ограничивает перемещения данного тела в пространстве, будем называть связью.

Например, тело лежащее на столе – несвободное тело. Связью его является плоскость стола, которая препятствует перемещению тела вниз.

Очень важен так называемый принцип освобождаемости, которым будем пользоваться в дальнейшем. Записывается он так:

Любое несвободное тело можно сделать свободным, если связи убрать, а действие их на тело заменить силами, такими, чтобы тело оставалось в равновесии.

Сила, с которой данная связь действует на тело, препятствуя тем ила иным его перемещениям, называется силой реакции (противодействия) связи или просто реакцией связи.

Так у тела, лежащего на столе, связь – стол. Тело несвободное. Сделаем его свободным – стол уберем, а чтобы тело осталось в равнове­сии, заменим стол силой, направленной вверх и равной, конечно, весу тела.

Направлена реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу. Когда связь одновременно препятствует перемещениям тела по нескольким направлениям, направление реакции связи также наперед неизвестно и должно определяться в результате решения рассматриваемой задачи.

Если в качестве физического тела рассматривать какой-либо элемент инженерного сооружения (балка, ферма, колонна, плита и т. п.), который передает давление на опоры, то реакции опор (связей) называют опорными реакциями. Реакции связей носят вторичное происхождение, они возникают как противодействие другим силам.

Все силы, кроме реакции связей, называют заданными силами. Термин «заданные силы» имеет глубокий смысл. Заданные силы чаще всего являются активными, т.е. силами, которые могут вызвать движение тел, например: сила тяжести, снеговая или ветровые нагрузки и т.п. Учитывая сказанное выше, будем подразделять силы на активные силы и реакции связей.

Для определения направления реакции необходимо установить особенности взаимодействия твердого тела со связями различного вида. Следует иметь в виду, что реакция всегда направлена противоположно направлению возможного перемещения тела при удалении связи.

Рассмотрим, как направлены реакции некоторых основных видов связей:

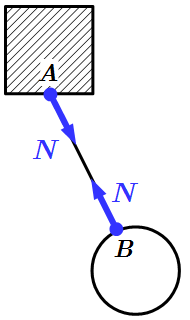
1. Гладкая плоскость (поверхность) или опора. Гладкой будем называть поверхность, трением о которую данного тела можно в первом приближении пренебречь. Такая поверхность не дает телу перемещаться только по направлению общего перпен­дикуляра (нормали) к поверхностям соприкасающихся тел в точке их касания (рис.11, а). Поэтому реакция N гладкой поверхности или опоры направлена по общей нормали к поверхностям сопри­касающихся тел в точке их касания и приложена в этой точке. Когда одна из соприкасающихся поверхностей является точкой (рис. 11, б), то реакция направлена по нормали к другой поверх­ности.

Источник