Что такое статистическая ошибка
Ошибки, встроенные в систему: их роль в статистике
В прошлой статье я указал, как распространена проблема неправильного использования t-критерия в научных публикациях (и это возможно сделать только благодаря их открытости, а какой трэш творится при его использовании во всяких курсовых, отчетах, обучающих задачах и т.д. — неизвестно). Чтобы обсудить это, я рассказал об основах дисперсионного анализа и задаваемом самим исследователем уровне значимости α. Но для полного понимания всей картины статистического анализа необходимо подчеркнуть ряд важных вещей. И самая основная из них — понятие ошибки.
Ошибка и некорректное применение: в чем разница?
В любой физической системе содержится какая-либо ошибка, неточность. В самой разнообразной форме: так называемый допуск — отличие в размерах разных однотипных изделий; нелинейная характеристика — когда прибор или метод измеряют что-то по строго известному закону в определенных пределах, а дальше становятся неприменимыми; дискретность — когда мы чисто технически не можем обеспечить плавность выходной характеристики.
И в то же время существует чисто человеческая ошибка — некорректное использование устройств, приборов, математических законов. Между ошибкой, присущей системе, и ошибкой применения этой системы есть принципиальная разница. Важно различать и не путать между собой эти два понятия, называемые одним и тем же словом «ошибка». Я в данной статье предпочитаю использовать слово «ошибка» для обозначения свойства системы, а «некорректное применение» — для ошибочного ее использования.
То есть, ошибка линейки равна допуску оборудования, наносящего штрихи на ее полотно. А ошибкой в смысле некорректного применения было бы использовать ее при измерении деталей наручных часов. Ошибка безмена написана на нем и составляет что-то около 50 граммов, а неправильным использованием безмена было бы взвешивание на нем мешка в 25 кг, который растягивает пружину из области закона Гука в область пластических деформаций. Ошибка атомно-силового микроскопа происходит из его дискретности — нельзя «пощупать» его зондом предметы мельче, чем диаметром в один атом. Но способов неправильно использовать его или неправильно интерпретировать данные существует множество. И так далее.
Так, а что же за ошибка имеет место в статистических методах? А этой ошибкой как раз и является пресловутый уровень значимости α.
Ошибки первого и второго рода
Ошибкой в математическом аппарате статистики является сама ее Байесовская вероятностная сущность. В прошлой статье я уже упоминал, на чем стоят статистические методы: определение уровня значимости α как наибольшей допустимой вероятности неправомерно отвергнуть нулевую гипотезу, и самостоятельное задание исследователем этой величины перед исследователем.
Вы уже видите эту условность? На самом деле, в критериальных методах нету привычной математической строгости. Математика здесь оперирует вероятностными характеристиками.
И тут наступает еще один момент, где возможна неправильная трактовка одного слова в разном контексте. Необходимо различать само понятие вероятности и фактическую реализацию события, выражающуюся в распределении вероятности. Например, перед началом любого нашего эксперимента мы не знаем, какую именно величину мы получим в результате. Есть два возможных исхода: загадав некоторое значение результата, мы либо действительно его получим, либо не получим. Логично, что вероятность и того, и другого события равна 1/2. Но показанная в предыдущей статье Гауссова кривая показывает распределение вероятности того, что мы правильно угадаем совпадение.
Наглядно можно проиллюстрировать это примером. Пусть мы 600 раз бросаем два игральных кубика — обычный и шулерский. Получим следующие результаты:
До эксперимента для обоих кубиков выпадение любой грани будет равновероятно — 1/6. Однако после эксперимента проявляется сущность шулерского кубика, и мы можем сказать, что плотность вероятности выпадения на нем шестерки — 90%.
Другой пример, который знают химики, физики и все, кто интересуется квантовыми эффектами — атомные орбитали. Теоретически электрон может быть «размазан» в пространстве и находиться практически где угодно. Но на практике есть области, где он будет находиться в 90 и более процентах случаев. Эти области пространства, образованные поверхностью с плотностью вероятности нахождения там электрона 90%, и есть классические атомные орбитали, в виде сфер, гантелей и т.д.
Так вот, самостоятельно задавая уровень значимости, мы заведомо соглашаемся на описанную в его названии ошибку. Из-за этого ни один результат нельзя считать «стопроцентно достоверным» — всегда наши статистические выводы будут содержать некоторую вероятность сбоя.
Ошибка, формулируемая определением уровня значимости α, называется ошибкой первого рода. Ее можно определить, как «ложная тревога», или, более корректно, ложноположительный результат. В самом деле, что означают слова «ошибочно отвергнуть нулевую гипотезу»? Это значит, по ошибке принять наблюдаемые данные за значимые различия двух групп. Поставить ложный диагноз о наличии болезни, поспешить явить миру новое открытие, которого на самом деле нет — вот примеры ошибок первого рода.
Но ведь тогда должны быть и ложноотрицательные результаты? Совершенно верно, и они называются ошибками второго рода. Примеры — не поставленный вовремя диагноз или же разочарование в результате исследования, хотя на самом деле в нем есть важные данные. Ошибки второго рода обозначаются буквой, как ни странно, β. Но само это понятие не так важно для статистики, как число 1-β. Число 1-β называется мощностью критерия, и как нетрудно догадаться, оно характеризует способность критерия не упустить значимое событие.
Однако содержание в статистических методах ошибок первого и второго рода не является только лишь их ограничением. Само понятие этих ошибок может использоваться непосредственным образом в статистическом анализе. Как?
ROC-анализ
ROC-анализ (от receiver operating characteristic, рабочая характеристика приёмника) — это метод количественного определения применимости некоторого признака к бинарной классификации объектов. Говоря проще, мы можем придумать некоторый способ, как отличить больных людей от здоровых, кошек от собак, черное от белого, а затем проверить правомерность такого способа. Давайте снова обратимся к примеру.
Пусть вы — подающий надежды криминалист, и разрабатываете новый способ скрытно и однозначно определять, является ли человек преступником. Вы придумали количественный признак: оценивать преступные наклонности людей по частоте прослушивания ими Михаила Круга. Но будет ли давать адекватные результаты ваш признак? Давайте разбираться.
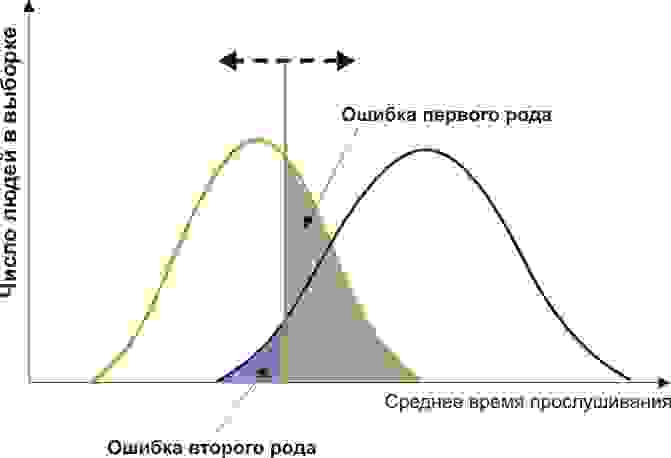
Вам понадобится две группы людей для валидации вашего критерия: обычные граждане и преступники. Положим, действительно, среднегодовое время прослушивания ими Михаила Круга различается (см. рисунок):
Здесь мы видим, что по количественному признаку времени прослушивания наши выборки пересекаются. Кто-то слушает Круга спонтанно по радио, не совершая преступлений, а кто-то нарушает закон, слушая другую музыку или даже будучи глухим. Какие у нас есть граничные условия? ROC-анализ вводит понятия селективности (чувствительности) и специфичности. Чувствительность определяется как способность выявлять все-все интересующие нас точки (в данном примере — преступников), а специфичность — не захватывать ничего ложноположительного (не ставить под подозрение простых обывателей). Мы можем задать некоторую критическую количественную черту, отделяющую одних от других (оранжевая), в пределах от максимальной чувствительности (зеленая) до максимальной специфичности (красная).
Посмотрим на следующую схему:
Смещая значение нашего признака, мы меняем соотношения ложноположительного и ложноотрицательного результатов (площади под кривыми). Точно так же мы можем дать определения Чувствительность = Полож. рез-т/(Полож. рез-т + ложноотриц. рез-т) и Специфичность = Отриц. рез-т/(Отриц. рез-т + ложноположит. рез-т).
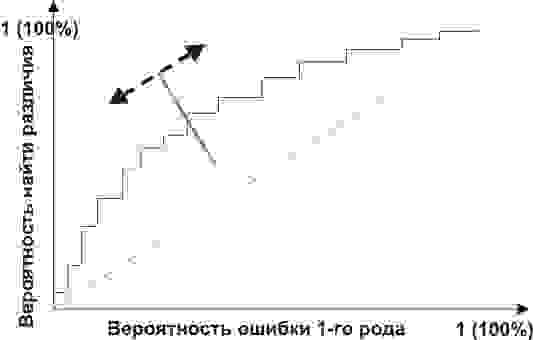
Но главное, мы можем оценить соотношение положительных результатов к ложноположительным на всем отрезке значений нашего количественного признака, что и есть наша искомая ROC-кривая (см. рисунок):
А как нам понять из этого графика, насколько хорош наш признак? Очень просто, посчитать площадь под кривой (AUC, area under curve). Пунктирная линия (0,0; 1,1) означает полное совпадение двух выборок и совершенно бессмысленный критерий (площадь под кривой равна 0,5 от всего квадрата). А вот выпуклость ROC кривой как раз и говорит о совершенстве критерия. Если же нам удастся найти такой критерий, что выборки вообще не будут пересекаться, то площадь под кривой займет весь график. В целом же признак считается хорошим, позволяющим надежно отделить одну выборку от другой, если AUC > 0,75-0,8.
С помощью такого анализа вы можете решать самые разные задачи. Решив, что слишком много домохозяек оказались под подозрением из-за Михаила Круга, а кроме того упущены опасные рецидивисты, слушающие Ноггано, вы можете отвергнуть этот критерий и разработать другой.
Возникнув, как способ обработки радиосигналов и идентификации «свой-чужой» после атаки на Перл-Харбор (отсюда и пошло такое странное название про характеристику приемника), ROC-анализ нашел широкое применение в биомедицинской статистике для анализа, валидации, создания и характеристики панелей биомаркеров и т.д. Он гибок в использовании, если оно основано на грамотной логике. Например, вы можете разработать показания для медицинской диспансеризации пенсионеров-сердечников, применив высокоспецифичный критерий, повысив эффективность выявления болезней сердца и не перегружая врачей лишними пациентами. А во время опасной эпидемии ранее неизвестного вируса вы наоборот, можете придумать высокоселективный критерий, чтобы от вакцинации в прямом смысле не ускользнул ни один чих.
С ошибками обоих родов и их наглядностью в описании валидируемых критериев мы познакомились. Теперь же, двигаясь от этих логических основ, можно разрушить ряд ложных стереотипных описаний результатов. Некоторые неправильные формулировки захватывают наши умы, часто путаясь своими схожими словами и понятиями, а также из-за очень малого внимания, уделяемого неверной интерпретации. Об этом, пожалуй, нужно будет написать отдельно.
Ошибки и остатки
СОДЕРЖАНИЕ
Введение [ править ]
В одномерных распределениях [ править ]
Если мы предположим нормально распределенную популяцию со средним значением μ и стандартным отклонением σ и выберем индивидуумов независимо, то мы имеем
и выборочное среднее
Икс ¯ знак равно Икс 1 + ⋯ + Икс п п <\ displaystyle <\ overline
случайная величина, распределенная таким образом, что:
В статистических ошибках затем
с ожидаемыми значениями нуля, [1] тогда как остатки равны
Замечание [ править ]
Регрессии [ править ]
Однако из-за поведения процесса регрессии распределения остатков в разных точках данных (входной переменной) могут различаться, даже если сами ошибки распределены одинаково. Конкретно, в линейной регрессии, где ошибки одинаково распределены, изменчивость остатков входных данных в середине области будет выше, чем изменчивость остатков на концах области: [6] линейные регрессии подходят для конечных точек лучше, чем середина. Это также отражается в функциях влияния различных точек данных на коэффициенты регрессии : конечные точки имеют большее влияние.
Другое использование слова «ошибка» в статистике [ править ]
Использование термина «ошибка», как обсуждалось в разделах выше, означает отклонение значения от гипотетического ненаблюдаемого значения. По крайней мере, два других использования также встречаются в статистике, оба относятся к наблюдаемым ошибкам прогнозирования:
Среднеквадратичная ошибка или среднеквадратичная ошибка (MSE) и среднеквадратичная ошибка (RMSE) относятся к тому, на сколько значения, предсказанные оценщиком, отличаются от оцениваемых величин (обычно за пределами выборки, по которой была оценена модель).
Ошибки при статистическом анализе: какие бывают и чем вызваны
Статистический анализ данных применительно к медицине – серьёзная наука, которая подчиняется определённым законам. И если им не следовать, результат будет неудовлетворительным. Статическая обработка данных в научном исследовании, продумывается ещё на этапе его планирования. Если же вспомнить о ней только по окончанию основной части работы, то систематизировать полученные данные будет практически невозможно. Даже специалистам будет весьма проблематично выудить из «кучи мусора» действительно важные показатели, чтобы исследователь получил ожидаемый результат. Поэтому, если вы не можете похвастаться высоким уровнем квалификации в биостатистике, обратиться за помощью к профессионалам в данном направлении, стоит ещё до начала экспериментальной работы. Это позволит избежать ошибок, которые могут поставить под сомнение результаты всего процесса.
Статистические ошибки – какими они бывают
Проведение любого эксперимента требует создания статистической выборке. О том, какими они бывают, на каких принципах строятся и их характеристики, вы можете прочесть в нашей статье. Статистическая обработка данных в научном исследовании и проводится на основании результатов, полученных в данных выборках. А затем, перекладывается на всю популяцию.
Объём выборки, напрямую связан с вероятностью появления статистических ошибок. Они бывают первого и второго рода.
Что касается ошибки второго рода, то показатель мощности, в большинстве случаев, имеет прямую зависимость от численности выборки. В больших по объёму группах, ниже вероятность ошибки второго рода и выше мощность статистических критериев. Данная зависимость является не менее чем квадратичной. Это значит, что при уменьшении объема выборки в два раза, последует падение мощности не менее чем в 4 раза. При этом, минимально допустимая мощность должна составлять не менее 80%, а максимально допустимый уровень ошибки – не выше 5%.
Стоит учитывать, что чётких границ не существует. Задаются они произвольно и в зависимости от особенностей исследования, его целей и характера, могут быть изменены. В большинстве случаев, научное сообщество произвольное изменение мощности, однако в подавляющем большинстве случаев уровень ошибки первого рода не может превышать 5%.
Особенности процедуры анализа
Статистическая обработка данных в научном исследовании предполагает соблюдение процедуры анализа. Он может осуществляться с использованием двух разновидностей техник – описательной или доказательной, которую ещё называют аналитической. Что касается описательных техник, то с их помощью, данные можно предоставить в компактном и понятном виде. Это могут быть графики, таблицы, абсолютные и относительные частоты, меры центральной тенденции, меры разброса данных и другие. Все они дают характеристику изучаемым выборкам.
Описание групп осуществляется по чётким критериям, и специалисты подбирают их совокупность индивидуально. Таким образом, результат получается максимально объективным. По завершению данного процесса, требуется выявить взаимоотношения между группами и, если это возможно, перенести результаты исследования на всю популяцию. Здесь в дело вступают аналитические методы биостатистики. Традиционно, данный этап специалисты называют «тестирование статистических гипотез».
При тестировании гипотез, все задачи разделяются на две большие группы. Работая с первой, необходимо выявить, есть ли различия между группами по уровню определённого показателя. Например – печеночных трансаминаз среди здоровых реципиентов и людей с подтверждённым гепатитом. А работая со второй группой, наличие связей исследуется уже не по одному, а нескольким параметрам. Для примера – функции печени и иммунной системы.
Если переменная, которая подлежит изучению, является качественной, сравниваются между собой две группы, то эффективно используется критерий «хи-квадрат». Стоит учитывать, что если наблюдений недостаточно, он будет непоказательным. В таком случае, применяются такие методы как поправка Йейтса на непрерывность и точный метод Фишера.
Что касается количественной переменной, то применяется один из двух видов статистических критериев. Так, критерии первого вида основываются на конкретном типе распределения генеральной совокупности и оперируют параметрами этой совокупности. Они имеют название «параметрические». А вот критерии второго вида – непараметрические, основываются на теории о типе распределения генеральной совокупности, и они не используют ее параметры. Иногда, их называют свободными от распределения. При этом важно учитывать, что распределения во всех сравниваемых группах должны быть идентичными, чтобы не получить ложноположительный результат.
Статистическая погрешность
Статистическая погрешность — это та неопределенность в оценке истинного значения измеряемой величины, которая возникает из-за того, что несколько повторных измерений тем же самым инструментом дали различающиеся результаты. Возникает она, как правило, из-за того, что результаты измерения в микромире не фиксированы, а вероятностны. Она тесно связана с объемом статистики: обычно чем больше данных, тем меньше статистическая погрешность и тем точнее результат измерения. Среди всех типов погрешностей она, пожалуй, самая безобидная: понятно, как ее считать, и понятно, как с ней бороться.
Статистическая погрешность: чуть подробнее
Предположим, что ваш детектор может очень точно измерить какую-то величину в каждом конкретном столкновении. Это может быть энергия или импульс какой-то родившейся частицы, или дискретная величина (например, сколько мюонов родилось в событии), или вообще элементарный ответ «да» или «нет» на какой-то вопрос (например, родилась ли в этом событии хоть одна частица с импульсом больше 100 ГэВ).
Это конкретное число, полученное в одном столкновении, почти бессмысленно. Скажем, взяли вы одно событие и выяснили, что в нём хиггсовский бозон не родился. Никакой научной пользы от такого единичного факта нет. Законы микромира вероятностны, и если вы организуете абсолютно такое же столкновение протонов, то картина рождения частиц вовсе не обязана повторяться, она может оказаться совсем другой. Если бозон не родился сейчас, не родился в следующем столкновении, то это еще ничего не говорит о том, может ли он родиться вообще и как это соотносится с теоретическими предсказаниями. Для того, чтобы получить какое-то осмысленное число в экспериментах с элементарными частицами, надо повторить эксперимент много раз и набрать статистику одинаковых столкновений. Всё свое рабочее время коллайдеры именно этим и занимаются, они накапливают статистику, которую потом будут обрабатывать экспериментаторы.
В каждом конкретном столкновении результат измерения может быть разный. Наберем статистику столкновений и усредним по ней результат. Этот средний результат, конечно, тоже не фиксирован, он может меняться в зависимости от статистики, но он будет намного стабильнее, он не будет так сильно прыгать от одной статистической выборки к другой. У него тоже есть некая неопределенность (в статистическом анализе она так и называется: «неопределенность среднего»), но она обычно небольшая. Вот эта величина и называется статистической погрешностью измерения.
Итак, когда экспериментаторы предъявляют измерение какой-то величины, то они сообщают результат усреднения этой величины по всей набранной статистике столкновений и сопровождают его статистической погрешностью. Именно такие средние значения имеют физический смысл, только их может предсказывать теория.
Есть, конечно, и иной источник статистической погрешности: недостаточный контроль условий эксперимента при повторном измерении. Если в физике частиц этот источник можно попытаться устранить, по крайней мере, в принципе, то в других разделах естественных наук он выходит на первый план; например, в медицинских исследованиях каждый человек отличается от другого по большому числу параметров.
Как считать статистическую погрешность?
Существует теория расчета статистической погрешности, в которую мы, конечно, вдаваться не будем. Но есть одно очень простое правило, которое легко запомнить и которое срабатывает почти всегда. Пусть у вас есть статистическая выборка из N столкновений и в ней присутствует n событий какого-то определенного типа. Тогда в другой статистической выборке из N событий, набранной в тех же условиях, можно ожидать примерно n ± √n таких событий. Поделив это на N, мы получим среднюю вероятность встретить такое событие и погрешность среднего: n/N ± √n/N. Оценка истинного значения вероятности такого типа события примерно соответствует этому выражению.
Сразу же, впрочем, подчеркнем, что эта простая оценка начинает сильно «врать», когда количество событий очень мало. В науке обсчета маленькой статистики есть много дополнительных тонкостей.
Более серьезное (но умеренно краткое) введение в методы статистической обработки данных в применении к экспериментам на LHC см. в лекциях arXiv.1307.2487.
Пример 1
Объем статистики имеет значение!
Продолжим этот пример. Предположим, вам такая точность показалась недостаточной, вам хочется уменьшить статистическую погрешность. В ситуации, когда и детектор, и методика отбора уже работают идеально, это можно сделать только одним способом — накопить побольше статистики.
Именно поэтому эксперименты в физике элементарных частиц стараются оптимизировать не только по энергии, но и по светимости. Ведь чем больше светимость, тем больше столкновений будет произведено — значит, тем больше будет статистическая выборка. И уже это позволит сделать измерения более точными — даже без каких-либо улучшений в эксперименте. Примерная зависимость тут такая: если вы увеличите статистику в k раз, то относительные статистические погрешности уменьшатся примерно в √k раз.
Пример 2
Если речь идет не просто о подсчетах событий, а об измерении непрерывной величины, то там статистическая погрешность тоже присутствует, но вычисляется она чуть сложнее.
Предположим, вы хотите измерить массу какой-то новой, только что открытой частицы. Частица эта рождается редко, и у вас из всей статистики набралось лишь четыре события рождения этой частицы. В каждом событии вы измерили ее массу, и у вас получилось четыре результата (мы здесь намеренно опускаем возможные систематические погрешности): 755 МэВ, 805 МэВ, 770 МэВ, 730 МэВ. Теперь можно взять область масс от 700 до 850 МэВ и поставить на ней эти четыре точки (рис. 1). Поскольку каждая точка отвечает одному событию с данной массой, мы каждой точке присваиваем погрешность ±1 событие. То, что массы разные, — совершенно нормально, поскольку у нестабильных частиц есть некая «размазка» по массе. Поэтому, согласно теории, ожидается некая плавная кривая, и когда физики говорят про массу нестабильной частицы, они имеют в виду положение максимума этой кривой. Она тоже показана на рис. 1, но только положение и ширина этой кривой заранее неизвестны, они определяются по наилучшему соответствию с данными.
Рис. 1. Данные из примера в виде «экспериментального» графика. Каждая точка отвечает одному событию при данной массе. Пунктирная кривая показывает типичное теоретическое ожидание для распределения «экспериментальных» точек
Из-за того что данных очень мало, мы можем провести эту кривую так, как показано на рисунке, а можем и немножко сместить ее в стороны — и так, и эдак будет осмысленное совпадение. Вычислив среднее значение массы, можно получить положение пика этой кривой, а также его неопределенность: 765 ± 15 МэВ. Эта неопределенность целиком и полностью обязана разным результатам измерений, она и является статистической погрешностью измерения.
Рис. 2. То же, что на рис. 1, но уже на статистике в 60 «экспериментальных» точек
Если мы наберем побольше событий рождения и распада этой частицы, мы сможем увеличить статистику. На рис. 2 показано, как мог бы выглядеть тот же график, если бы у нас уже было 60 событий. Распределение событий по массе начинает приобретать какую-то форму, которая действительно отдаленно напоминает широкий пик, спадающий по краям.
Рис. 3. Сечение процесса e + e – → π + π – в области энергий от 700 до 850 МэВ, в которой четко проступают ρ-мезон и ω-мезон. Здесь собраны данные восьми экспериментов, изучавших этот процесс. Статистические погрешности измерений детектора BaBar едва заметны глазом. Изображение из статьи arXiv:1010.4180
Сейчас этот процесс изучен вдоль и поперек, статистика набрана огромная (миллионы событий), а значит, и масса ρ-мезона сейчас определена несравнимо точнее. На рис. 3 показано современное состояние дел в этой области масс. Если ранние эксперименты еще имели какие-то существенные погрешности, то сейчас они практически неразличимы глазом. Огромная статистика позволила не только измерить массу (примерно равна 775 МэВ с точностью в десятые доли МэВ), но и заметить очень странную форму этого пика. Такая форма получается потому, что практически в том же месте на шкале масс находится и другой мезон, ω(782), который «вмешивается» в процесс и искажает форму ρ-мезонного пика.
Другой, гораздо более реальный пример влияния статистики на процесс поиска и изучения хиггсовского бозона обсуждался в новости Анимации показывают, как в данных LHC зарождался хиггсовский сигнал.