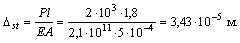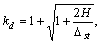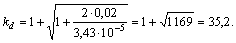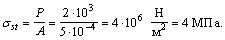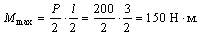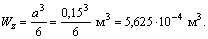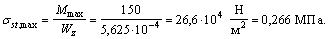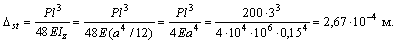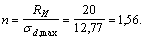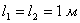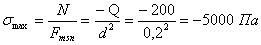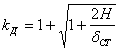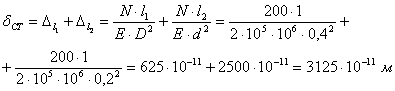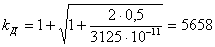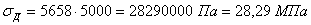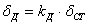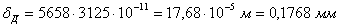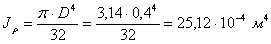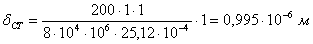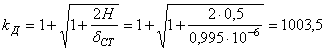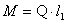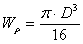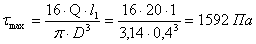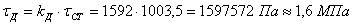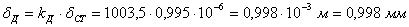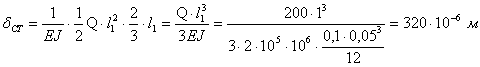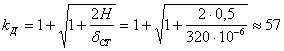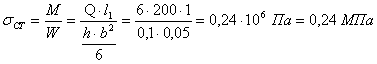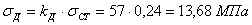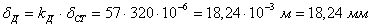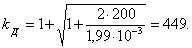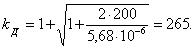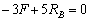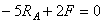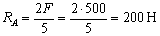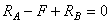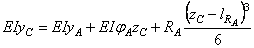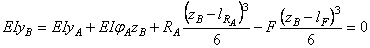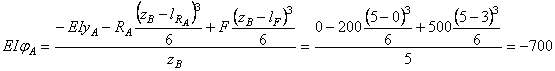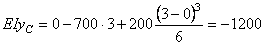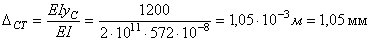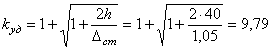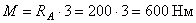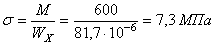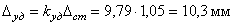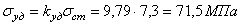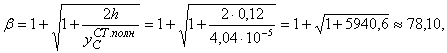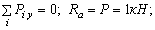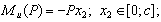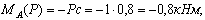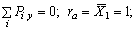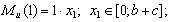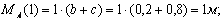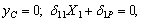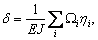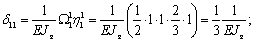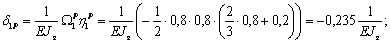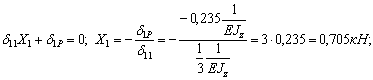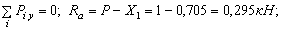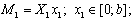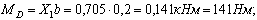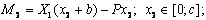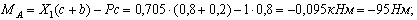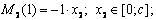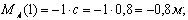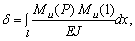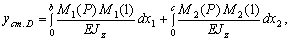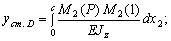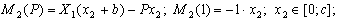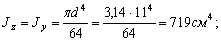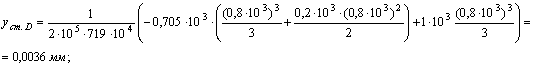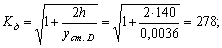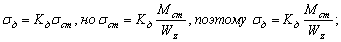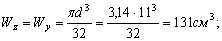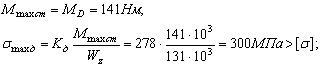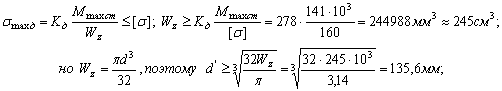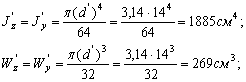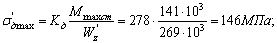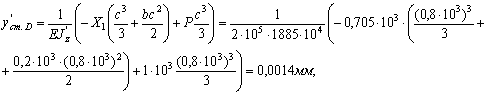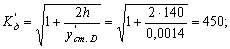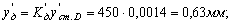Что такое статистический прогиб

Лекция 15 (продолжение). Примеры решения на динамические нагрузки

Расчеты при ударных нагрузках

Пример 1.

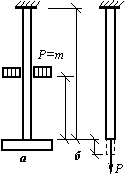
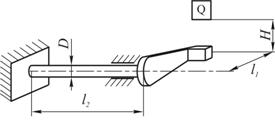
Груз весом Р = 2 кН, скользя без трения вдоль стального бруса, падает на приваренную к нему жесткую пластину и вызывает ударное растяжение бруса. Площадь поперечного сечения бруса А = 0,0005 м 2 (рис. а ), его длина l = 1,8 м, модуль продольной упругости материала бруса Е =2·10 5 МПа; высота падения груза Н равна 0,02 м.

SHAPE \* MERGEFORMAT

Определим величину 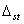(рис. б)

Рассчитываем динамический коэффициент, используя формулу

Определяем статическое нормальное напряжение

Находим максимальное динамическое напряжение

.

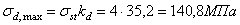
Проводим статический расчет, т.е. определяем максимальное напряжение и перемещение в серединном сечении балки при нагружении ее статической сосредоточенной силой Р = 200 Н.

Максимальный изгибающий момент равен

Статический момент площади сечения равен

Определяем максимальное нормальное статическое напряжение

Статическое перемещение посередине балки определяем по известной из теории изгиба формуле

Рассчитываем динамический коэффициент

Находим динамическое напряжение

МПа.

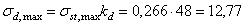
Запас прочности равен

Для заданной упругой системы определить:

— величину перемещения в направлении удара в том сечении, в котором прикладывается ударная нагрузка в направлении удара.

Рассмотрим различные примеры ударного нагружения.

Осевое действие ударной нагрузки.

Длины участков

Динамические напряжения в стальном стержне определяются по формуле

При статическом приложении нагрузки 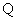в месте удара в любом сечении стержня будет возникать продольная сила

Знак минус указывает на сжимающее нормальное напряжение.

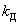
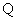
Коэффициент динамичности зависит от высоты падения груза и статической деформации

Статическая деформация 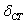будет складываться из деформаций участков

Максимальное динамическое напряжение

Динамическая деформация сечения, в котором прикладывается ударная нагрузка

Предварительно определим статические значения напряжения и перемещения.

,

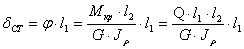
Коэффициент динамичности

Максимальное статическое напряжение при действии закручивающего момента

.

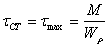
Определим максимальное напряжение и величину перемещения сечения в месте приложения ударной нагрузки.

Статическое перемещение определим способом Верещагина

Максимальное статическое напряжение будет возникать в опорном сечении

.

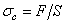
Вес груза ,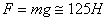

Статическое напряжение .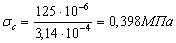

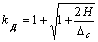
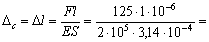
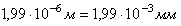
Коэффициент динамичности (без учета собственной массы стержня), где статическая деформация

.

Коэффициент динамичности

Для жесткого стержня единицами в формуле 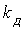можно было бы пренебречь.

Для дюралюминиевого стержня

,

.

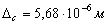
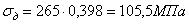
Таким образом, замена материала позволяет снизить напряжения в 1,69 раза.

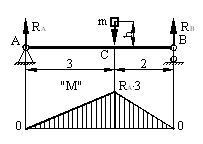
Определяем опорные реакции

;

;

;

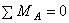
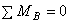
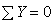
Определяем статический прогиб балки

Прогиб балки определим по методу начальных параметров.

Составляем уравнение прогибов для точки С

Определяем начальные параметры

Находим прогиб в точке С

Определяем ударный коэффициент

Определяем напряжения в балке от статического действия нагрузки

Изгибающий момент будет иметь максимальное значение в точке С (см. рис.), а его величина определится по формуле:

Тогда напряжения в точке С:

Определяем динамический прогиб и напряжения

Коэффициент динамичности при ударе вычисляется по формуле

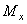
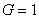
1. Строим эпюру изгибающих моментов от силы кН, приложенной к балке статически.

Отсюда находим, что

Тогда изгибающий момент под сосредоточенной силой равен:

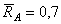
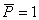
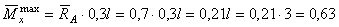
В этом случае и тогда ордината единичной эпюры моментов под силой равна

м.

4. Коэффициент динамичности равен :

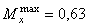
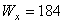
5. Вычисляем наибольшее статическое напряжение, возникающее в поперечном сечении балки ( кНм = 63 кНсм ; см 3 ):

6. Вычисляем наибольшее динамическое напряжение в балке:

Прочность балки при ударе обеспечена, поскольку

Определить динамические напряжения в опасных сечениях ба­лок. Сравнить полученные напряжения с теми, которые появятся в балках, если балка КD будет опираться на абсолютно жесткое осно­вание.

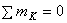
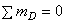
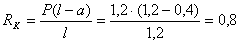
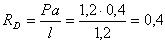
Из уравнений равновесия балки и находим опорные реакции R_K , R_{D :}

кН;

кН.

Затем строим эпюры изгибающих моментов и поперечных сил для рассматриваемой балки КD и двух консольных балок АК и DМ (рис. 1, б, в, г, д, е).

Сначала определим статический прогиб сече­ния С балки КD при опирании ее на абсолютно жесткое основание. Составим уравнение прогиба методом начальных параметров, при­няв начало координат в сечении К:

. (1)

; .

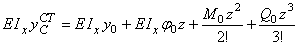
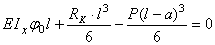
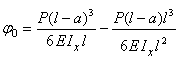
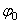
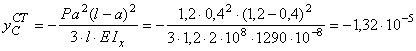
Теперь, подставив найденное значение в уравнение (1), получим формулу для определения прогиба сечения С :

м.

Для определения полного прогиба сечения С с учетом упругого характера опирания балки КD (рис. 1, ж) необходимо предварительно найти прогибы концов консольных балок АК и DМ. Для этого воспользуемся фор­мулой, полученной в примере 34:

м ;

м.

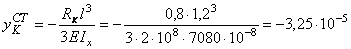
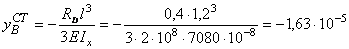
Эпюра перемещений для составной конструкции из балок изо­бражена на рис. 1, ж. Величину полного перемещения сечения С балки с учетом перемещения его в результате смещения опор балки КD, опирающейся на консольные балки, определяем по формуле:

.

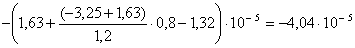
Динамический коэффициент при падении груза G на балку КD, опирающуюся на консольные балки АК и DМ, опреде­ляем по формуле:

.

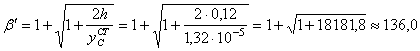
Для вычисления динамических напряжений необходимо внача­ле определить статические напряжения, возникающие в сечении С:

а затем динамические напряжения:

.

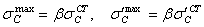
Динамические напряжения, возникающие в сечении С балки КD, опирающейся на консольные балки,

и динамические напряжения, возникающие в сечении С балки КD, опирающейся на абсолютно жесткое основание:

Таким образом, если опоры лежат на абсолютно жестком осно­вание, то в сечении С возникают динамические напряжения в 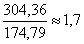раза большие по величине. Статические напряжения, возникающие в сечении А:

При динамическом коэффициенте К_Д = 78,1, полученном в предположении упругого опирания балки КD в точках К и D, нахо­дим динамические напряжения в сечении А:

Статическое и динамическое напряжения в сечении М балки DМ:

Следовательно, вне зависимости от того, на какое основание опирается балка KD, опасное сечение находится в точке удара.

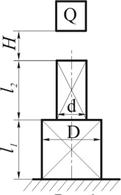
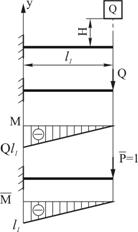
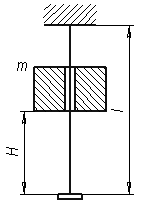
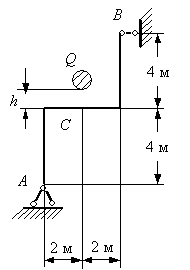
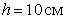
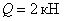
На раму, показанную на рис. 1, падает груз Q с высоты . Вес груза , поперечное сечение рамы – двутавр № 20. Требуется найти максимальные нормальные напряжения в опасном сечении рамы и прогиб в точке удара от ударного действия нагрузки.

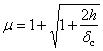
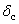
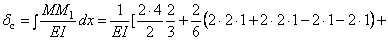
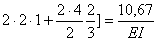
Чтобы определить динамический коэффициент по формуле , необходимо найти прогиб точки С (точки приложения нагрузки Q ) от статического действия нагрузки. Найдем этот прогиб, используя метод Максвелла–Мора и интегрируя формулу Максвелла–Мора с помощью правила Верещагина. Для этого построим эпюры изгибающих моментов от нагрузки Q (рис. 2, а) и от единичной силы, соответствующей искомому перемещению (рис. 2, б). Перемножим эти эпюры по правилу Верещагина:

.

Подставляя величину жесткости для двутавра № 20, сосчитаем прогиб в «см»

.

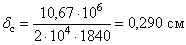
Найдем динамический коэффициент по формуле

.

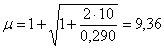
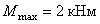
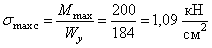
Определим максимальные нормальные напряжения в опасном сечении от статического действия нагрузки. В рассматриваемом примере несколько равно опасных сечений с изгибающим моментом . Максимальные статические напряжения равны

.

Динамические напряжения от действия ударной нагрузки увеличатся согласно формуле 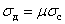в раз.

.

Видно, что динамические напряжения не превосходят предела пропорциональности 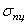= 200 МПа, и материал работает упруго.

Во столько же раз увеличится и динамический прогиб:

.

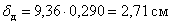
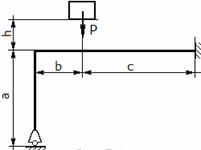
Дано: на раму падает груз весом P с некоторой высоты h (рис.1)

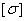
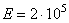
материал – сталь, = 160 МПа, МПа;

a = 0,6 м, b = 0,2 м, c = 0,8 м; d = 11 см, P = 1 кН, h = 14 см;

1) раскрыть статическую неопределимость рамы;

2) определить динамический коэффициент;

3) определить динамические напряжения и прогибы;

1. Раскрытие статической неопредимости рамы

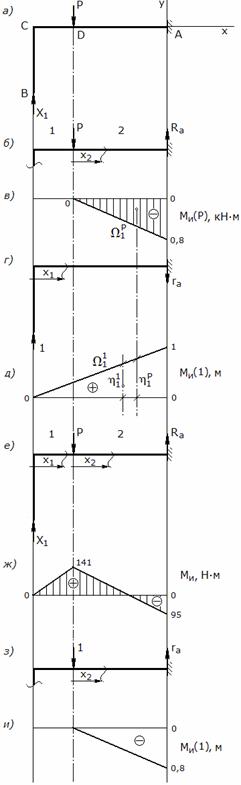
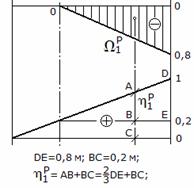
Выбираем эквивалентную систему, отбрасывая реакцию катка и заменяя ее неизвестной силой X ₁ (рис. 2, а).

а) построение грузовой эпюры

Изгибающий момент от статической силы P на 2 участке будет:

в сечении D момент равен 0, в сечении A :

Строим эпюру моментов от силы P (рис. 2, в).

б) построение эпюры моментов от единичной силы

Вместо неизвестной X ₁ прикладываем единичную силу 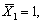и рассматриваем ее действие на раму (рис. 2, г). Реакция заделки в этом случае равна:

Изгибающий момент от единичной силы равен:

в сечении C момент равен 0, в сечении A :

Строим эпюру моментов от единичной силы (рис.2, д).

в) решение канонического уравнения

В сечении B приложения неизвестной реакции прогиб равен 0 (т.к. катковая опора препятствует вертикальному перемещению), поэтому и в сечении C прогиб равен 0, т.е. суммарный прогиб от действия неизвестной реакции X ₁ и силы P равен 0:

Находим прогибы способом Верещагина:

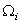
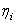
где – площадь фигуры на грузовой эпюре, – ордината под центром тяжести этой фигуры на эпюре единичной силы.

Находим прогиб от единичной силы: площадью фигуры в формуле Верещагина будет площадь эпюры единичной силы, ординатой – ордината под центром тяжести эпюры единичной силы (2/3 высоты эпюры); поэтому:

Находим прогиб от силы P : площадью фигуры будет площадь грузовой эпюры, ординатой – ордината на эпюре единичной силы под центром тяжести грузовой эпюры (рис. 3); поэтому:

Тогда, решая каноническое уравнение получаем:

Неизвестная реакция X ₁ равна по величине 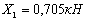и направлена по направлению единичной силы.

2. Определение статического прогиба и динамического коэффициента

а) построение эпюры изгибающих моментов

Определяем реакцию заделки A с учетом реакции отброшенной опоры (рис. 2, е):

Изгибающий момент на 1 участке равен:

в сечении C момент равен 0, в сечении D :

Изгибающий момент на 2 участке:

в сечении А момент равен:

Строим эпюру изгибающих моментов (рис. 2, ж).

б) построение эпюры единичной силы

В сечении D прикладываем единичную силу и рассматриваем ее действие на раму (рис. 2, з). Момент от единичной силы возникает только на 2 участке рамы:

в сечении D момент равен 0, в сечении A :

Строим эпюру изгибающего момента от единичной силы (рис. 2, и).

в) определение статического прогиба

Определяем статический прогиб с помощью интеграла Мора:

где M _и( P ), M _и(1) – изгибающие моменты, возникающие под действием силы P и единичной силы.

но т.к. на 1 участке единичная сила момента не создает, то первое слагаемое обращается в ноль:

с учетом моментов, создаваемых силой P и единичной силой на 2 участке получаем:

Учитывая, что сечение рамы круглое, находим его момент инерции:

тогда статический прогиб равен:

Вычисляем динамический коэффициент по приближенной формуле:

3. Определение динамических напряжений и прогибов

Динамические напряжения определяются как:

Учитывая, что сечение рамы круглое, находим его момент сопротивления:

Считая статический изгибающий момент максимальным, действующим в сечениях рамы, находим максимальные динамические напряжения:

Таким образом, максимальные динамические напряжения превышают допустимые напряжения 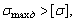подбираем новое сечение рамы, исходя из условия прочности:

Округляем диаметр нового сечения рамы до стандартного 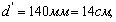выбранного из ряда Ra 40 нормальных линейных размеров (ГОСТ 6636–69), тогда для нового сечения:

Максимальные динамические напряжения, возникающие в раме с новым сечением:

Определяем статический прогиб для рамы с новым сечением:

Пересчитываем динамический коэффициент:

Динамический прогиб в сечении падения груза будет:

Онлайн-калькулятор «Расчет коэффициента динамичности при падении груза на конструкцию»

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Источник