Что такое степень вершины графа
Степень вершины (теория графов)
Содержание
Лемма о рукопожатиях
По формуле суммы степеней для графа 
то есть сумма степеней вершин любого графа равна удвоенному числу его рёбер. Кроме того, формула утверждает, что в любом графе число вершин нечётной степени чётно. Данное утверждение (и сама формула) известны как лемма о рукопожатиях. Название происходит от известной математической задачи: необходимо доказать, что в любой группе число людей, пожавших руку нечётному числу других чётно.
Последовательность степеней вершин
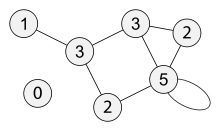
Последовательность степеней вершин неориентированного графа является невозрастающей последовательностью. [2] Для графа, изображённого на рис. 1, она имеет вид (5, 3, 3, 2, 2, 1, 0). Последовательность степеней вершин есть инвариант графа, поэтому у изоморфных графов она одинакова. Однако последовательность степеней вершин не является уникальной характеристкой графа: в некоторых случаях неизоморфные графы также обладают одинаковой последовательностью.
Проблема последовательности степеней заключается в нахождении некоторых или всех графов с заданной невозрастающей последовательностью, состоящей из натуральных чисел (нулевые степени при этом могут быть проигнорированы, так как их количество изменяется добавлением или удалением изолированных вершин). Последовательность, являющаяся последовательностью степеней какого-либо графа, называется графической (англ. graphical sequence ). Из формулы суммы степеней следует, что любая последовательность с нечётной суммой (как, к примеру, 3, 3, 1) не может быть последовательностью степеней графа. Обратное также верно: если последовательность имеет чётную сумму, она представляет собой последовательность степеней мультиграфа. Построение такого графа осуществляется достаточно простым способом: необходимо объединить вершины нечётных степеней в пары, к оставшимся незаполненными вершинам следует добавить петли.
Сложнее реализовать простой граф с заданной последовательностью. Теорема Эрдёша — Галлаи утверждает, что невозрастающая последовательность di (при i = 1,…,n) может быть последовательностью простого графа только если её сумма чётна и выполняется неравенство
Например, последовательность (3, 3, 3, 1) не может являться последовательностью простого графа; она удовлетворяет неравенству Эрдёша — Галлаи только при k равном 1, 2 или 4, но не при k равном 3.
С. Л. Хакими доказал, что (d1, d2, …, dn) есть последовательность степеней простого графа только если существует (d2 − 1, d3 − 1, …, dd1+1 − 1, dd1+2, dd1+3, …, dn). Этот факт позволил разработать простой алгоритм нахождения простого графа с заданной реализуемой последовательностью:
Проблема нахождения или оценки числа графов по заданной последовательности относится к области перечисления графов.
Частные значения
Общие свойства
См. также
Примечания
Источники
Полезное
Смотреть что такое «Степень вершины (теория графов)» в других словарях:
Дуга (теория графов) — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Цикл (теория графов) — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Дерево (теория графов) — У этого термина существуют и другие значения, см. Дерево (значения). Дерево это связный ациклический граф.[1] Связность означает наличие путей между любой парой вершин, ацикличность отсутствие циклов и то, что между парами вершин… … Википедия
Графов теория — раздел конечной математики (См. Конечная математика), особенностью которого является геометрический подход к изучению объектов. Основное понятие теории граф. Граф задаётся множеством вершин (точек) и множеством рёбер (связей), соединяющих … Большая советская энциклопедия
Глоссарий теории графов — Эта страница глоссарий. См. также основную статью: Теория графов Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице) … Википедия
Словарь терминов теории графов — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С … Википедия
Практическое применение раскраски графов — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей. Раскраска графов практически применяется (постановку задачи различиных раскрасок здесь обсуждаться не будет) дл … Википедия
Теоремы теории графов — Здесь собраны теоремы из теории графов. Содержание 1 Лемма о рукопожатиях 2 Существование эйлерова пути и цикла … Википедия
Вершина (граф) — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Длина пути в орграфе — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Основные сведения из теории графов.
Вершины в графе могут отличаться друг от друга тем, скольким ребрам они принадлежат.
Степенью вершины называется число ребер графа, которым принадлежит эта вершина.
Обозначать степени вершин Л, В, С будем соответственно так: степ. А у степ. В, степ. С и т. п.
У графа на рисунке степ. А = 1; степ. В = 2.
Теорема. В графе Г сумма степеней всех его вершин —число четное, равное удвоенному числу ребер графа.
Теорема. Число нечетных вершин любого графа четно.
Пример. В графе Г вершины Л и В — связные, а вершины А и Н — несвязные.
1. Одинаковое ли число вершин на обоих рисунках?
2. Одинаковое ли на них число ребер?
3. Одинаковое ли на них число вершин имеет степень k?
Сформулируем необходимое и достаточное условие соответствия двух рисунков одному и тому же графу. Они изображают один и тот же граф тогда и только тогда, когда между вершинами на первом и на втором рисунках существует такое взаимно однозначное соответствие, при котором:
1) две вершины графа на первом рисунке соединены ребром, если соединена ребром соответствующая пара вершин графа на втором рисунке;
2) две вершины графа на втором рисунке соединены ребром, если соединена ребром соответствующая пара вершин графа на первом рисунке.
Деревом называется всякий связный граф, не имеющий циклов (см. рис.):
Теорема. Дерево с в вершинами имеет в — 1 ребро.
Одни графы можно нарисовать на плоскости так, чтобы их ребра не имели общих точек, кроме вершин, им принадлежащих; другие графы так нарисовать нельзя. В силу этого отдельные графы могут рассматриваться как
На рисунке изображен граф Г: некоторые ребра его пересекаются.
Рисунок графа, в котором никакие два его ребра не пересекаются, если не считать точками пересечения общие вершины, называют плоским представлением графа. Ясно, что плоское представление имеет только плоский граф. Обратно, у всякого плоского графа непременно найдется плоское представление. Плоские графы — простые циклы, деревья, лес, а также и граф, содержащий цикл, из вершин которого «выходят» деревья.
Примером не плоского графа может служить полный граф с пятью вершинами. Любые попытки нарисовать его плоское представление обречены на неудачу.
Сформулируем теорему о плоских графах
Теорема (Понтрягина — Куратовского). Граф является плоским тогда и только тогда, когда он не имеет подграфом графа типа I или типа II.
Граф, все ребра которого ориентированы, называется ориентированным графом.
Ориентированный граф изображен на рисунке
Степенью выхода вершины А ориентированного графа называется число выходящих из А ребер (обозначение: степ.вых.А).
Степенью входа вершины А ориентированного графа называется число входящих в А ребер (обозначение: степ.вх.А).
В графе на рисунке:
степ.вых.С = 0; степ.вх.С = 3;
степ.выx.F = 0; степ.вх. F = 0.
В ориентированных графах в зависимости от сочетания степеней входа и выхода для данной вершины будем рассматривать три частных случая.
Изолированной вершиной называется вершина, у которой и степень входа и степень выхода равны 0.
Источником называется вершина, степень выхода которой положительна, а степень входа равна 0.
Стоком называется вершина, степень входа которой положительна, а степень выхода равна 0.
На рисунке вершина F — изолированная, D — источник, С — сток.
Теория графов — основы
График — это диаграмма точек и линий, соединенных с точками. У него есть по крайней мере одна линия, соединяющая набор из двух вершин без вершин, соединяющих себя. Понятие графов в теории графов опирается на некоторые основные термины, такие как точка, линия, вершина, ребро, степень вершин, свойства графов и т. Д. Здесь, в этой главе, мы рассмотрим эти основы теории графов.
точка
Точка — это конкретная позиция в одномерном, двухмерном или трехмерном пространстве. Для лучшего понимания точку можно обозначить алфавитом. Его можно обозначить точкой.
пример
Здесь точка — это точка с именем «а».
Линия
Линия — это связь между двумя точками. Это может быть представлено сплошной линией.
пример
Здесь «а» и «б» являются точками. Связь между этими двумя точками называется линией.
пример
Здесь вершина названа с алфавитом «а».
Ребро — это математический термин для линии, соединяющей две вершины. Многие ребра могут быть сформированы из одной вершины. Без вершины ребро не может быть сформировано. Для ребра должна быть начальная и конечная вершина.
пример
Здесь «a» и «b» — две вершины, и связь между ними называется ребром.
график
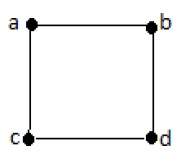
Граф ‘G’ определяется как G = (V, E), где V — множество всех вершин, а E — множество всех ребер графа.
Пример 1
В приведенном выше примере ab, ac, cd и bd являются ребрами графа. Аналогично, a, b, c и d являются вершинами графа.
Пример 2
В этом графе есть четыре вершины a, b, c и d и четыре ребра ab, ac, ad и cd.
петля
В графе, если ребро нарисовано от вершины к себе, это называется циклом.
Пример 1
На приведенном выше графике V — вершина, для которой у нее есть ребро (V, V), образующее петлю.
Пример 2
В этом графе есть две петли, которые сформированы в вершине a, и вершине b.
Степень вершины
Это число вершин, смежных с вершиной V.
Обозначение — град (V).
В простом графе с n числом вершин степень любых вершин равна —
Степень вершины можно рассматривать по двум случаям графов —
Степень вершины в неориентированном графе
Ненаправленный граф не имеет направленных ребер. Рассмотрим следующие примеры.
Пример 1
Посмотрите на следующий график —
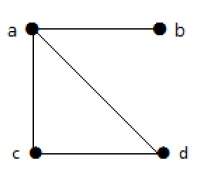
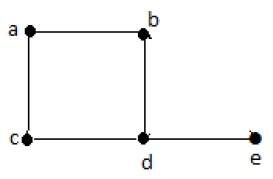
На приведенном выше неориентированном графике
deg (a) = 2, поскольку в вершине ‘a’ встречаются 2 ребра.
deg (b) = 3, поскольку в вершине ‘b’ встречаются 3 ребра.
deg (c) = 1, поскольку в вершине ‘c’ сформировано 1 ребро
deg (d) = 2, поскольку в вершине ‘d’ встречаются 2 ребра.
deg (e) = 0, так как в вершине ‘e’ есть 0 ребер.
deg (a) = 2, поскольку в вершине ‘a’ встречаются 2 ребра.
deg (b) = 3, поскольку в вершине ‘b’ встречаются 3 ребра.
deg (c) = 1, поскольку в вершине ‘c’ сформировано 1 ребро
deg (d) = 2, поскольку в вершине ‘d’ встречаются 2 ребра.
deg (e) = 0, так как в вершине ‘e’ есть 0 ребер.
Пример 2
Посмотрите на следующий график —
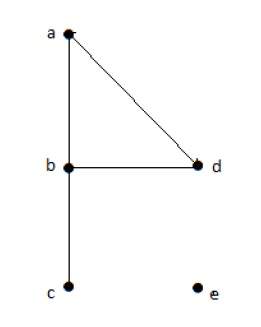
На приведенном выше графике
deg (a) = 2, deg (b) = 2, deg (c) = 2, deg (d) = 2 и deg (e) = 0.
Вершина «е» является изолированной вершиной. Граф не имеет никакой вершины.
Степень вершины в ориентированном графе
В ориентированном графе каждая вершина имеет степень и степень.
Степень графа
Степень вершины V — это количество ребер, входящих в вершину V.
Обозначение — град — (V).
Степень вершины V — это количество ребер, входящих в вершину V.
Обозначение — град — (V).
Степень графа
Отступ вершины V — это число ребер, выходящих из вершины V.
Обозначение — град + (V).
Отступ вершины V — это число ребер, выходящих из вершины V.
Обозначение — град + (V).
Рассмотрим следующие примеры.
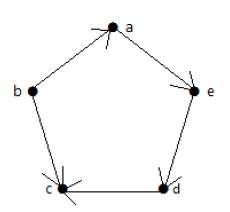
Пример 1
Посмотрите на следующий ориентированный граф. Вершина «а» имеет два ребра, «ad» и «ab», которые идут наружу. Следовательно, его степень равна 2. Аналогично, существует ребро «ga», идущее к вершине «a». Следовательно, степень «а» равна 1.
Степень и степень других вершин показаны в следующей таблице:
| темя | полустепень захода | полустепень |
|---|---|---|
| 1 | 2 | |
| б | 2 | 0 |
| с | 2 | 1 |
| d | 1 | 1 |
| е | 1 | 1 |
| е | 1 | 1 |
| г | 0 | 2 |
Пример 2
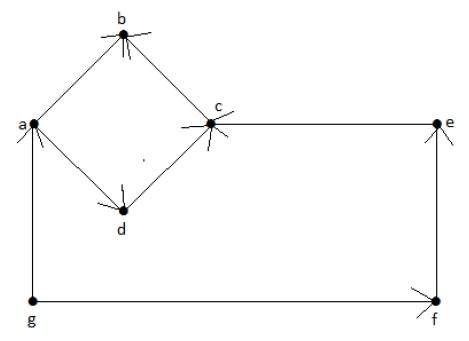
Посмотрите на следующий ориентированный граф. Вершина ‘a’ имеет ребро ‘ae’, идущее наружу от вершины ‘a’. Следовательно, его степень равна 1. Аналогично, у графа есть ребро «ba», приближающееся к вершине «a». Следовательно, степень «а» равна 1.
Степень и степень других вершин показаны в следующей таблице:
| темя | полустепень захода | полустепень |
|---|---|---|
| 1 | 1 | |
| б | 0 | 2 |
| с | 2 | 0 |
| d | 1 | 1 |
| е | 1 | 1 |
Кулон Вертекс
Используя степень вершины, мы получаем два специальных типа вершин. Вершина с первой степенью называется нерешенной вершиной.
пример
Здесь, в этом примере, вершина ‘a’ и вершина ‘b’ имеют соединенное ребро ‘ab’. Таким образом, что касается вершины «a», то к вершине «b» имеется только одно ребро, и аналогично по отношению к вершине «b» есть только одно ребро к вершине «a». Наконец, вершина ‘a’ и вершина ‘b’ имеют степень как единицу, которая также называется висячей вершиной.
Изолированная вершина
Вершина с нулевой степенью называется изолированной вершиной.
пример
Здесь вершина «a» и вершина «b» не имеют связи между собой, а также с любыми другими вершинами. Таким образом, степень обеих вершин ‘a’ и ‘b’ равна нулю. Они также называются изолированными вершинами.
смежность
Вот нормы смежности —
В графе две вершины называются смежными, если между двумя вершинами есть ребро. Здесь смежность вершин поддерживается одним ребром, соединяющим эти две вершины.
В графе два ребра называются смежными, если между двумя ребрами есть общая вершина. Здесь смежность ребер поддерживается единственной вершиной, соединяющей два ребра.
В графе две вершины называются смежными, если между двумя вершинами есть ребро. Здесь смежность вершин поддерживается одним ребром, соединяющим эти две вершины.
В графе два ребра называются смежными, если между двумя ребрами есть общая вершина. Здесь смежность ребер поддерживается единственной вершиной, соединяющей два ребра.
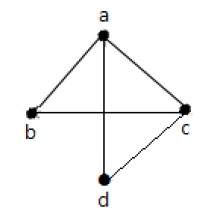
Пример 1
На приведенном выше графике —
«a» и «b» — это смежные вершины, так как между ними есть общее ребро «ab».
«a» и «d» являются смежными вершинами, так как между ними есть общее ребро «ad».
ab ‘и’ be ‘- смежные ребра, так как между ними есть общая вершина’ b ‘.
be ‘и’ de ‘- смежные ребра, так как между ними есть общая вершина’ e ‘.
«a» и «b» — это смежные вершины, так как между ними есть общее ребро «ab».
«a» и «d» являются смежными вершинами, так как между ними есть общее ребро «ad».
ab ‘и’ be ‘- смежные ребра, так как между ними есть общая вершина’ b ‘.
be ‘и’ de ‘- смежные ребра, так как между ними есть общая вершина’ e ‘.
Пример 2
На приведенном выше графике —
a ‘и’ d ‘являются смежными вершинами, так как между ними есть общее ребро’ ad ‘.
‘c’ и ‘b’ являются смежными вершинами, так как между ними есть общее ребро ‘cb’.
‘ad’ и ‘cd’ являются смежными ребрами, так как между ними есть общая вершина ‘d’.
ac ‘и’ cd ‘являются смежными ребрами, так как между ними есть общая вершина’ c ‘.
a ‘и’ d ‘являются смежными вершинами, так как между ними есть общее ребро’ ad ‘.
‘c’ и ‘b’ являются смежными вершинами, так как между ними есть общее ребро ‘cb’.
‘ad’ и ‘cd’ являются смежными ребрами, так как между ними есть общая вершина ‘d’.
ac ‘и’ cd ‘являются смежными ребрами, так как между ними есть общая вершина’ c ‘.
Параллельные края
В графе, если пара вершин соединена более чем одним ребром, то эти ребра называются параллельными ребрами.
На приведенном выше графике «a» и «b» — это две вершины, которые соединены между собой двумя ребрами «ab» и «ab». Так это называется параллельным ребром.
Мульти График
Граф, имеющий параллельные ребра, называется мультиграфом.
Пример 1
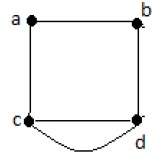
На приведенном выше графике есть пять ребер «ab», «ac», «cd», «cd» и «bd». Поскольку ‘c’ и ‘d’ имеют два параллельных ребра между ними, это мультиграф.
Пример 2
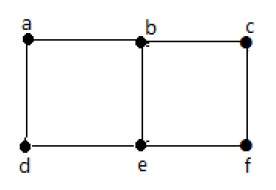
На приведенном выше графике вершины «b» и «c» имеют два ребра. Вершины ‘e’ и ‘d’ также имеют два ребра между ними. Следовательно, это мультиграф.
Степень последовательности графика
Если степени всех вершин в графе расположены в порядке убывания или возрастания, то полученная последовательность называется последовательностью графа графа.
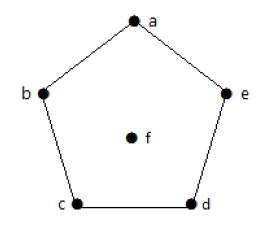
Пример 1
| темя | б | с | d | е | |
|---|---|---|---|---|---|
| Присоединенный к | До нашей эры | объявление | объявление | с, Ь, е | d |
| степень | 2 | 2 | 2 | 3 | 1 |
На приведенном выше графике для вершин
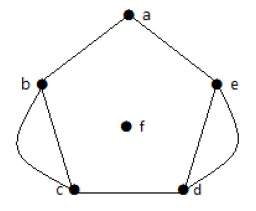
Пример 2
| темя | б | с | d | е | е | |
|---|---|---|---|---|---|---|
| Присоединенный к | быть | а, с | б, г | с, е | объявление | — |
| степень | 2 | 2 | 2 | 2 | 2 | 0 |
На приведенном выше графике для вершин