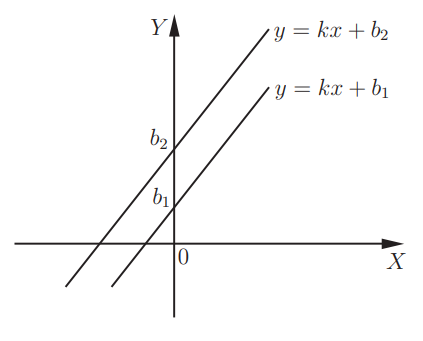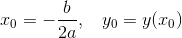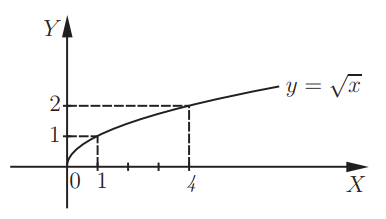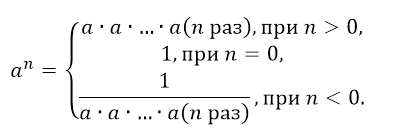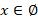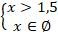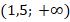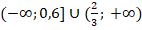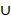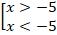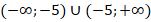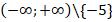Что такое степенная функция это

Степенная функция

Содержание

Вещественная функция

Область определения

Если показатель степени — целое число, то можно рассматривать степенную функцию на всей числовой прямой (кроме, возможно, нуля). В общем случае степенная функция определена при 0″ border=»0″ />. Если 0″ border=»0″ />, то функция определена также и при , иначе нуль является её особой точкой.

Рациональный показатель степени

Пример: из третьего закона Кеплера вытекает, что период T обращения планеты вокруг Солнца связан с большой полуосью A её орбиты соотношением: (полукубическая парабола).

Свойства

Комплексная функция

Степенная функция комплексного переменного z, вообще говоря, определяется формулой [3] :

Здесь показатель степени c — некоторое комплексное число. Значение функции, соответствующее главному значению логарифма, называется главным значением степени. Например, значение равно где k — произвольное целое, а его главное значение есть

Комплексная степенная функция обладает значительными отличиями от своего вещественного аналога. В силу многозначности комплексного логарифма она, вообще говоря, также имеет бесконечно много значений. Однако два практически важных случая рассматриваются отдельно.

См. также

Литература

Ссылки

Примечания

Полезное

Смотреть что такое «Степенная функция» в других словарях:

Степенная функция — функция f (x) = ха, где а фиксированное число (см. Степень). При действительных значениях основания х и показателя а обычно рассматривают лишь действительные значения С. ф. xa. Они существуют, во всяком случае, для всех х > 0; если а… … Большая советская энциклопедия

СТЕПЕННАЯ ФУНКЦИЯ — функция вида y = axn, где a и n любые действительные числа … Большой Энциклопедический словарь

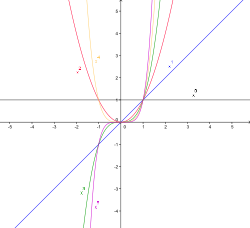
СТЕПЕННАЯ ФУНКЦИЯ — ф ция вида у = ахn, где а и п действит. числа, С. ф. охватывает большое число закономерностей в природе. На рис. изображены графики С. ф. для п = 1, 2, 3, 1/2 и а = 1. К ст. Степенная функция … Большой энциклопедический политехнический словарь

степенная функция — функция вида у=axn, где а и n любые действительные числа. На рисунке изображены графики степенной функции для n = 1, 2, 3, 1/2 и а = 1. * * * СТЕПЕННАЯ ФУНКЦИЯ СТЕПЕННАЯ ФУНКЦИЯ, функция вида y = axn, где a и n любые действительные числа … Энциклопедический словарь

степенная функция — laipsninė funkcija statusas T sritis automatika atitikmenys: angl. power function vok. Potenzfunktion, f rus. степенная функция, f pranc. fonction puissance, f … Automatikos terminų žodynas

СТЕПЕННАЯ ФУНКЦИЯ — функция вида у = ахn, где а и п любые действительные числа. На рис. изображены графики С. ф. для n= 1, 2, 3, 1/2 и a=1 … Естествознание. Энциклопедический словарь

функция спроса — Функция, которая показывает, как меняется объем продаж конкретного продукта в зависимости от его цены при равных маркетинговых усилиях по его продвижению на рынок. [http://www.lexikon.ru/dict/fin/a.html] функция спроса Функция, отражающая… … Справочник технического переводчика

Функция спроса — [demand function] функция, отражающая зависимость объема спроса на отдельные товары и услуги (потребительские блага) от комплекса факторов, влияющих на него. Более узкая трактовка: Ф.с.выражает взаимозависимость между спросом на товар и ценой… … Экономико-математический словарь

Источник

Свойства степенных функций, построение графиков

Степенная функция — что это такое

К степенным функциям в теории относятся следующие виды:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Исходя из обозначения, при x≥0, область определения рассматриваемой функции – это луч [0;+∞).

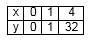
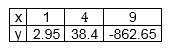
Далее следует записать таблицу значений:

Затем можно сравнить несколько степенных функции следующим способом:

Число 2,5 находится между 2 и 3. В таком случае можно предположить, что и график рассматриваемой функции расположен между соответствующими графиками. Можно представить разные характеристики х, чтобы сравнить значения функций, которые зависят от x:

Все графики целесообразно построить на одном рисунке. В первом случае \(0 :

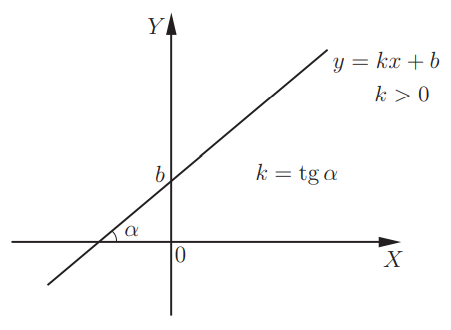
Линейная функция y = kx + b. Графиком данной функции является прямая линия. Для того, чтобы ее построить, требуется пара точек. При k > 0, линейная функция будет расти. При увеличении k график становится круче. Значение k представляет собой угловой коэффициент прямой и равно тангенсу угла наклона рассматриваемой прямой к положительному направлению оси X:

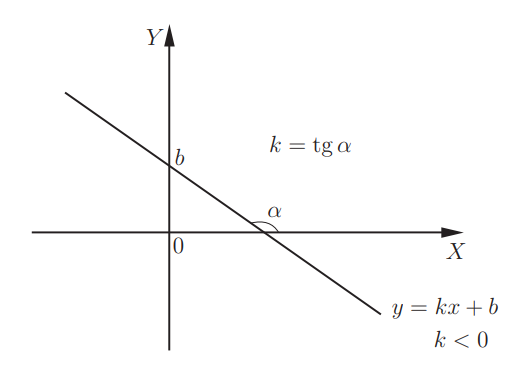
При использовании k

При k = 0, на графике будет изображена прямая y = b, которая параллельна оси X. В том случае, когда имеет место равенство угловых коэффициентов прямых, прямые будут параллельны друг другу.

Квадратичная функция \(y = ax2 + bx + c\) представляет собой параболу. Она обладает рядом особенностей:

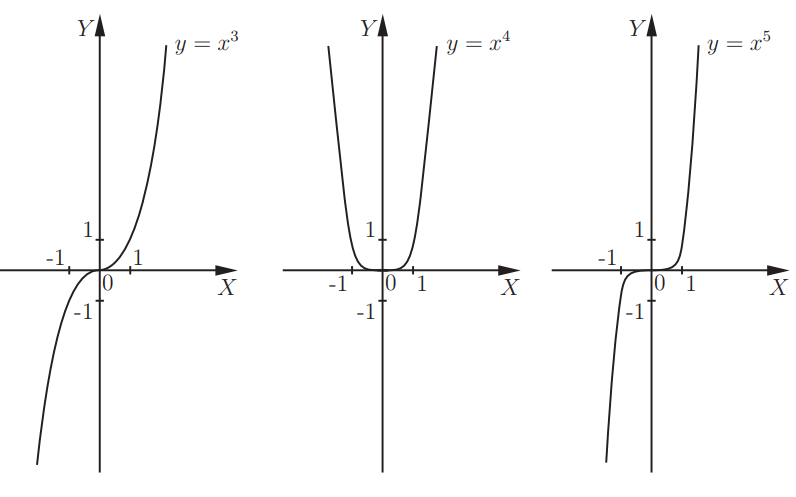
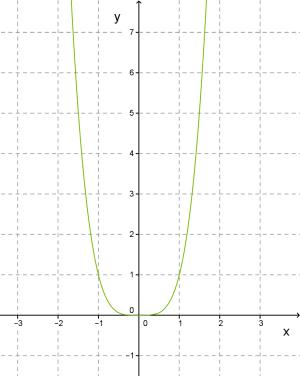
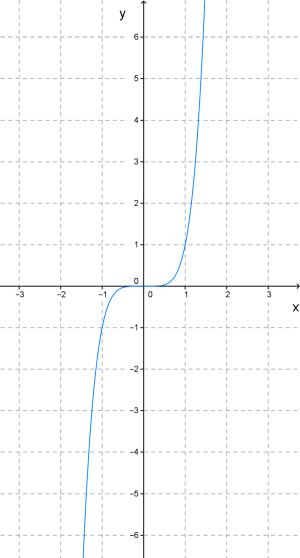
Функция \(y = x^<3>\) является кубической параболой. Можно представить ее на рисунке, а также функции \( y = x^<4>\) и \(y = x^<5>.\)

Можно отметить, что функции \(y = x^<2>\) и \(y = x^<4>\) обладают некоторыми сходствами. Графики являются симметричными по отношению к оси Y. В данном случае можно сказать, что рассматриваемые функции – четные.

Функция \(y = f(x)\) является четной, когда:

Графики функций \(y = x^<3>\) и \(y = x^<5>\) симметричны по отношению к началу координат. Данные функции являются нечетными.

Функция \(y = f(x)\) – нечетная, при условии, что:

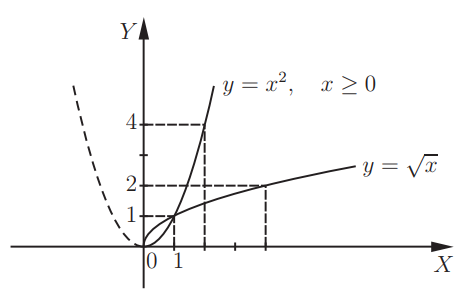
То, что для одной из них является областью определения, для другой — представляет собой область значений. Данные функции носят название взаимно-обратных.

Виды и их свойства, область определения

Степенные функции обладают рядом специфических свойств, которые могут отличаться в зависимости от их вида. Рассмотрим основные из них.

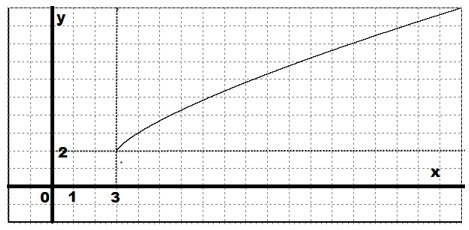
График имеет следующий вид:

В том случае, когда x>0, а r – какое-либо рациональное число, производная степенной функции \(y=x^r\) определяется, согласно формуле:

Степенная функция с рациональным и иррациональным показателем

Степень действительного числа a, обладающего рациональным показателем n вычисляется, согласно уравнению:

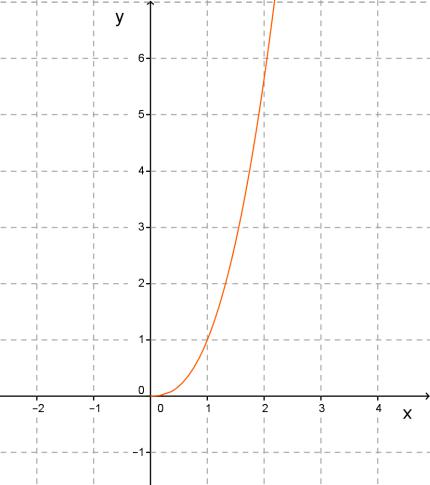
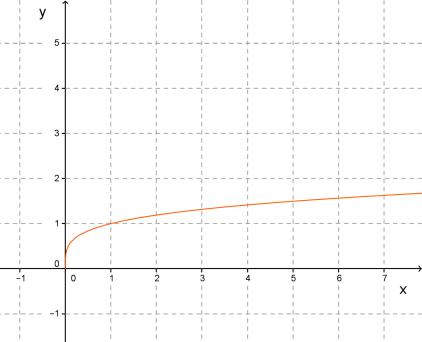
Функция \( f(x)=x^(r\in Q)\) представляет собой степенную функцию с рациональным показателем.

Функция \(f(x)=x^(r\in J)\) представляет собой степенную функцию с иррациональным показателем.

Как строить графики степенных функций

График функции является множеством точек, у которых абсциссы являются допустимыми значениями аргумента х, а ординаты – соответствующими значениями функции y.

Согласно определению, построить график какой-либо функции можно путем поиска всех пар соответствующих значений аргумента и функции. Как правило, в результате получается бесконечное множество точек, что затрудняет процесс построения графика. В связи с этим требуется исследовать функцию:

Задачи со степенной функцией

Необходимо определить максимальное и минимальное значения для функции \(y=x^<\frac<5><2>>\) на отрезке:

Показатель степени рассматриваемой функции обладает положительным значением. В этом случае, учитывая свойства записанной функции, можно заключить, что она возрастает на всей области определения. Таким образом, функция достигает своего максимума и минимума на концах заданных отрезков (если она определена в этих точках).

На промежутке (2,10) максимальное и минимальное значения функции отсутствуют, в связи с тем, что промежуток является открытым, и точки 0 и 4 к данному интервалу не относятся.

На луче [9;+∞) наибольшее значение отсутствует

Требуется определить максимальное и минимальное значение на отрезке [1;9] для функции:

Вычислим производную рассматриваемой функции:

Так как производная существует на всей области определения исходной функции, можно заключить, что критические точки отсутствуют.

Далее определим стационарные точки:

Заданному отрезку принадлежит только одно решение \(x_2=4\)

Построим таблицу значений нашей функции на концах отрезка и в точке экстремума:

График функции \(y=x^<\frac<4><3>>\) будет возрастать, а график функции \(у=24-х\) – убывать. Известно, что когда одна функция возрастает, а вторая убывает, то будет лишь одна точка, в которой эти функции пересекаются. Следовательно, уравнение обладает всего одним решением. Можно заметить, что:

Таким образом, при х=8 уравнение преобразуется в справедливое равенство: 16=16, что является ответом к задаче.

Необходимо построить график функции с объяснениями: \(y=(x-3)^\frac<3><4>+2\)

График рассматриваемой функции можно получить из графика функции:

Требуется сместить этот график на 3 единицы в правую сторону и на 2 единицы вверх:

Требуется записать уравнение для касательной к прямой \(y=x^<-\frac<4><5>>\) в точке х=1.

Обозначение уравнения касательной:

По условию задачи число a является натуральным числом 1, поэтому:

Источник

Функция. Степенная функция.

Так как нулевая степень всякого числа, не равного нулю, равна единице, то при n = 0 степенная функция становится постоянной величиной, т.е. у = а. Поясним подробнее: выражение ноль в нулевой степени неопределенно, в том случае, когда функция у = ax 0 для всех значений х, естественно кроме нуля, равна а, и следовательно, если х = 0, то у = а. В таком случае график представлен прямой линией, параллельной оси абсцисс).

Остальные случаи делятся на группы:

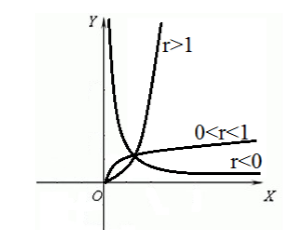
Видны графики функции у = х n при n = 0,1; 1/4; 1/3; 1/2; 2/3; 1;3/2; 2 ; 3; 4; 10. Все они проходят через начало координат и точку (1; 1).

При n = 1 получаем прямую являющуюся биссектрисой угла х0у.

При n > 1 график образуется сначала между х = 0 и х = 1, несколько ниже этой прямой, а затем при х > 1, выше ее.

По аналогии с графиком функции у = ах 2 графики всех степенных функций у = ах n при положительном n называют параболами n-го порядка или n-й степени. Так, график функции у = ах 3 называется параболой 3-го порядка или кубической параболой.

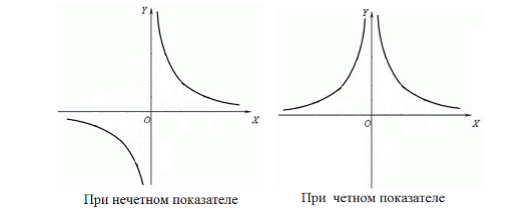
В случае если n дробное число p/q с четным знаменателем q и нечетным числителем р, то величина может иметь два знака , а у графика появляется еще одна часть внизу оси абсцисс х, причем она симметрична верхней части.

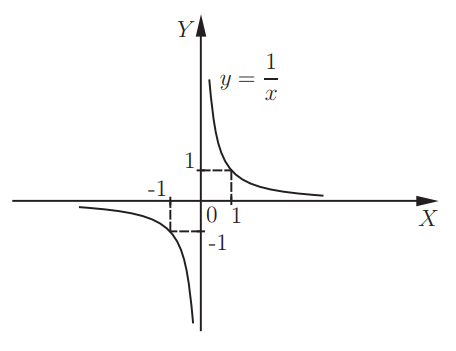
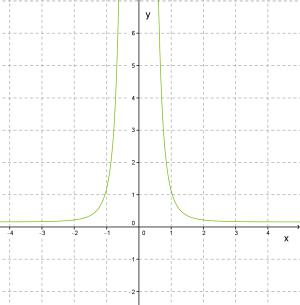
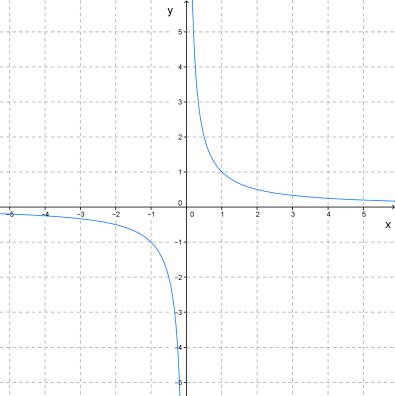
Все графики неограниченно приближаются как к оси абсцисс х, так и к оси ординат у, не соприкасаясь с ними. Вследствие сходства с гиперболой эти графики называют гиперболами n -го порядка.

Источник

Степенная функция

Вы будете перенаправлены на Автор24

Для удобства рассмотрения степенной функции будем рассматривать 4 отдельных случая: степенная функция с натуральным показателем, степенная функция с целым показателем, степенная функция с рациональным показателем и степенная функция с иррациональным показателем.

Степенная функция с натуральным показателем

Для начала введем понятие степени с натуральным показателем.

Рассмотрим теперь степенную функцию с натуральным показателем, её свойства и график.

$f\left(x\right)=x^n$ ($n\in N)$ называется степенной функцией с натуральным показателем.

Свойства степенной функции с натуральным четным показателем

$f(x)\ge 0$ на всей области определения

Функция выпукла на всей области определения.

Поведение на концах области определения:

Готовые работы на аналогичную тему

Свойства степенной функции с натуральным нечетным показателем

Функция возрастает на всей области определения.

\[2\left(2n-1\right)\left(n-1\right)\cdot x^<2n-3>=0\] \[x=0\]

Степенная функция с целым показателем

Для начала введем понятие степени с целым показателем.

Рассмотрим теперь степенную функцию с целым показателем, её свойства и график.

$f\left(x\right)=x^n$ ($n\in Z)$ называется степенной функцией с целым показателем.

Свойства степенной функции с отрицательным целым показателем

Если показатель четный, то функция четна, если нечетный, то функция нечетна.

$f(x)\ge 0$ на всей области определения

Степенная функция с рациональным и иррациональным показателем

$f\left(x\right)=x^r$ ($r\in Q)$ называется степенной функцией с рациональным показателем.

$f\left(x\right)=x^r$ ($r\in J)$ называется степенной функцией с иррациональным показателем.

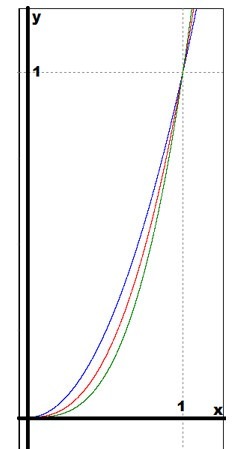
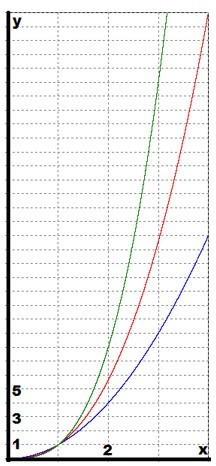
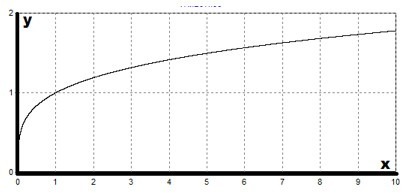
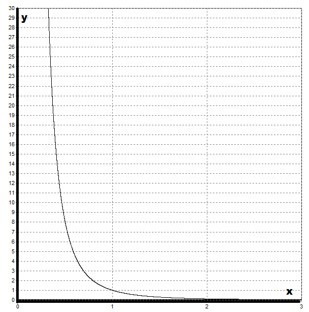
Приведем графики степенных функций с рациональным и иррациональным показателем (рис. 5). Рассмотреть, аналогично, свойства этих функции оставим читателю.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 22 03 2021

Источник

Описание степенных функций: виды, свойства, графики

Точная наука математика (в переводе с древнего греческого обозначает «предмет обучения») включает целый ряд дисциплин, издавна достаточно изученных, развивающихся и появившихся недавно. «Кто овладел творениями Архимеда, будет меньше удивляться открытиям самых великих людей нашего времени» – так написал Г.В. Лейбниц, что актуально и сегодня. При штудировании раздела математики степенные функции, как и остальных тем, разбираются изначально более простые объекты, постепенно переходят к сложным, не оставляя непонятного.

Что это такое? Основные понятия и определения

Азы алгебраического анализа математики станут пошагово яснее с помощью основных первичных понятий, определений, правил. Так на Рис.1 отображены термины и обозначения (понятийные ключи) направлений при переходе от «Начало» к исследованию функций для переменных в алгебре, к другим разделам царицы наук.

Обучение начинается от простых математических терминов – изначальных определений:

Переменная – символ в математике, свободная величина (аргумент функции), может принимать любое из ряда значений фиксированной области (вес зависит от возраста теленка, x в алгебре);

Функция – соответствие (зависимость) между «связанными» изменяемыми элементами; каждое значение зависимой функции определяется конкретной независимой величиной (переменной). Или же это формула, отображающая здравый смысл зависимости переменных (в математике обозначается y= f(x));

Степень – для общего случая, какая-либо мера в сравнении, в алгебре – это выражение, служащее для упрощения многократного умножения основания x (числа, переменной, функции ) на самое себя (пример обозначения: x^2). Количество одинаковых множителей называется показателем степени. В алгебре показатели степени могут быть целыми (четными и нечетными), дробными и иррациональными;

Иррациональное число представляют как непериодическую бесконечную десятичную дробь (число = 3,1415926535…);

Производная – тоже функция (вторичная), образованная от первичной, обозначается Y= f’(x) (как скоростная характеристика движения, как угол наклона касательной к линии);

Степенная функция – это функциональная зависимость вида f(x)=. Например, кубическая (объем) функционально зависит от длины ребра куба (x), его третьей степени (y=).

Виды, свойства и область определения

Разделяют зависимости (f(x)) на простые (элементарные) и сложные. Степенная функция относится к ряду элементарных.

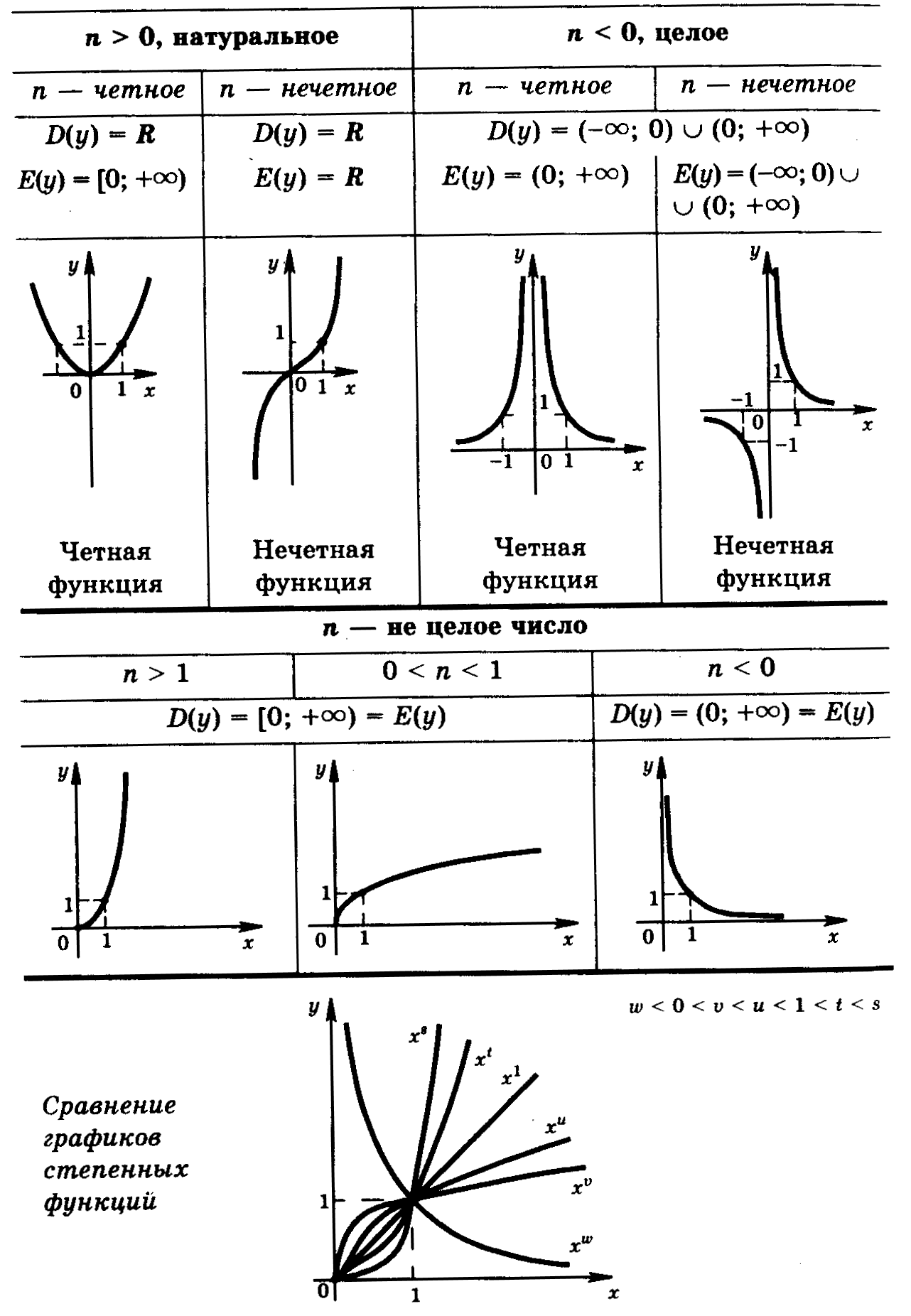
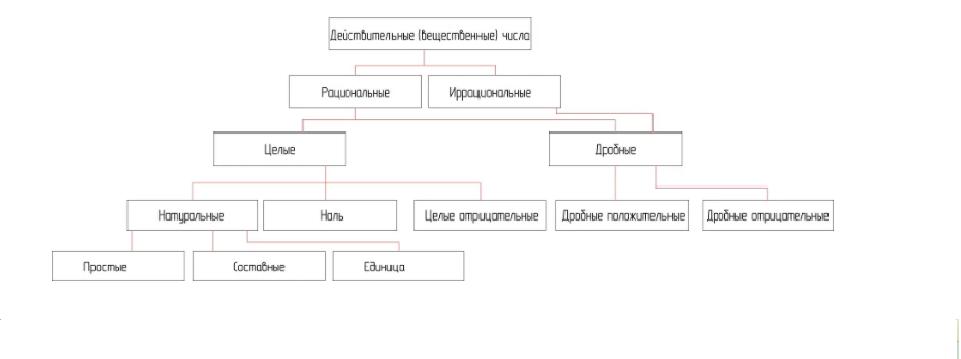
По показателю степени (характеристике числа) определяются присущие свойства степенной функции. На Рис.2 приведена классификация множества вещественных чисел. Собственно вид построения функционального степенного графика с целым натуральным или отрицательным показателем зависит как от знака, так и от четности числа показателя. Частных случаев действительных чисел (типовых) в показателе степени насчитывается более десятка.

Для сложных соответствий присуще применение к переменной нескольких функциональных «воздействий», при этом получается, как будто новая функция берется от другой «функции-аргумента». При фиксировании функциональных зависимостей используются следующие способы:

Табличный (значения «икса» в соответствии с «игреком» для заданной f (x));

Функция с целым плюсовым показателем степени при четном n будет четной, а при нечетном n – нечетной. Множество величин переменных относится в свойствах зависимостей к области определения (как определяется совокупность аргументов x). Величины допустимых итогов функции (y) на определенных участках фиксируются как диапазон значений.

Линейную зависимость общего вида y = kx + b можно считать степенной с показателем степени n=1. Если n=0, x≠0 (т.к. ноль в нулевой степени не определено), то функция становится константой-единицей. Особенность функций с 2k целым минусовым показателем – симметричность около оси ординат, четность. Для функций с целым 2k-1 показателем 1 (Рис.6,9), − 1 0 рисунке: положительные, отрицательные, целые, четные, нечетные, дробные).

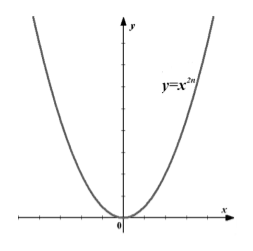
Рис.6 y=х^п, п-четное, вид параболы.

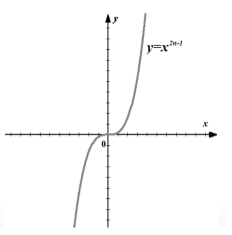
Рис.7 y=x^n. n-нечетное, вид кубической параболы.

Рис.8 y=х^(-n), когда — чётное число

Рис.9 y =х^(-n), когда — нечётное число

Рис.10 y=х^(m\п)m\п—неправильная дробь

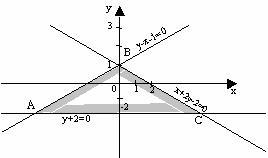
Квадратичные неравенства с 2 переменными:

Решая попарно уравнения прямых (пересечение), находятся три вершины треугольника С, В, А.

Для С – у=-2; х=6. Для В – х=0;у=1. Для А – у=-2; х=-3.

Найти подходящий к системе неравенств участок координатной плоскости.

Неравенства в системе верны в области точек нижнего полукруга и линии контура (Рис.4).

Проверим подстановкой (-0.2;-0.2) 0.08 0,

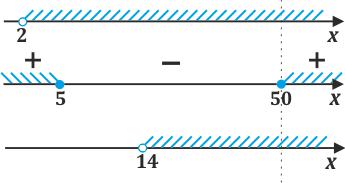
Отмечаются на числовой оси промежутки по результатам трех отношений (Рис.5 ).

После объединения для всех неравенств подходит «луч» из точки ≥50.

Для помощи при решении квадратичных неравенств, используя равнозначно соответствующее уравнение ax 2 + bx + c = у, с дискриминантом D = b 2 − 4ac, предлагается табличный алгоритм нахождения участков переменных x в зависимости от знаков коэффициента a и D. Причем старший коэффициент а≠0. Необходимо находить корни при положительном D для разложения на множители, упрощения, использования метода интервалов.

Как записать общее решение?

Сообразно четкой математической формулировке, отображению решения используются дополнительные условные символы. При вычислении результатов объединенных неравенств ищется пересечение решений, когда их нет, то ответом является пустое множество x:

Если встречается «пустое» неравенство, то результат находится хотя бы из одного уравнения системы.

Если отношение строгое, тогда отрезок решения считается открытым, со скобками ( ), без включения на отрезки пограничных точек. Если – нестрогое, то решение будет закрытым отрезком, включающим граничные точки.

Если из всего целого интервала исключают точку 5, то возможно оформление со знаком \:

Откроется еще много новых понятий, определений, знаковых обозначений благодаря осознанному изучению математических наук.

Приведены не все типы из многообразия неравенств, могут быть более сложные. Для их решения необходимо научиться разбираться в применяемых методах и способах специалистам, которые встречаются с необходимостью оптимизации процессов, допусками и ограничениями, учетом влияния нескольких параметров (математики, программисты, физики, экономисты).

Источник