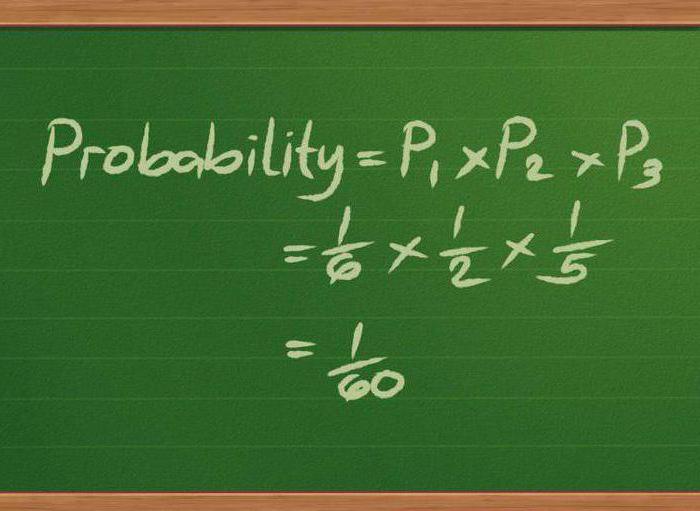Что такое стохастика в математике

26.10.202304.05.2022 admin 0 Comments

«Стохастический» – это слово, которое физики, математики и другие ученые используют для описания процессов, обладающих элементом случайности. Происхождение его древнегреческое. В переводе оно означает «умеющий угадывать».

Значение слова «стохастический»

Таким образом, можно заметить, что техническое значение данного понятия не точно соответствует его словарному (лексическому) значению. Некоторые авторы используют выражение «стохастический процесс» как синоним понятия «случайный процесс».

Стохастичность в математике

Употребление данного термина в математике в настоящее время широко распространено. К примеру, существует такое понятие в теории вероятности, как стохастический процесс. Его итог нельзя определить по изначальному состоянию данной системы.

Употребление в математике понятия «стохастичность» относят к трудам Владислава Борцкевича. Именно он использовал данный термин в значении «выдвигать гипотезы». В математике, в особенности в таком разделе этой науки, как теория вероятности, область случайных исследований играет большую роль. Существует, к примеру, такое понятие, как стохастическая матрица. Колонки или строки данной матрицы в сумме дают единицу.

Стохастическая математика (финансовая)

Данный раздел математики анализирует финансовые структуры, действующие в условиях неопределенности. Он призван находить самые рациональные методы управления финансовыми средствами и структурами, учитывая такие факторы, как стохастическая эволюция, риск, время и др.

В науке принято выделять следующие структуры и объекты, которые используются в финансовой математике в целом:

Основным объектом изучения финансовой математики стохастической является именно последний из них. Данный раздел базируется на таких дисциплинах, как статистика случайных процессов, теория случайных процессов и др.

В настоящее время даже людям, далеким от науки, хорошо известно по многочисленным новостям и публикациям в СМИ, что значения так называемых глобальных финансовых индексов (например, индекса Доу Джонса), цены акций меняются хаотически. Л. Башелье предпринял первую попытку описать с использованием математики эволюцию стоимости акций. Его стохастический метод опирается на теорию вероятностей. Диссертация Л. Башелье, где представлена эта попытка, была опубликована в 1900 году. Ученый доказал формулу, известную в настоящее время как формула справедливой стоимости опциона-колл. В ней отражается стохастическая вероятность.

Важные идеи, которые в дальнейшем привели к возникновению теории эффективного рынка, были изложены в труде М. Кендалла, изданном в 1953 году. В этой работе рассматривается вопрос динамики цен акций. Исследователь описывает ее с помощью стохастических процессов.

Стохастичность в физике

Благодаря физикам Э. Ферми, С. Уламу, Н. Метрополису и Д. Нейману большое распространение получил метод Монте-Карло. Его название произошло от казино, расположенного в одноименном городе такой страны, как Монако. Именно здесь занимал деньги для игры дядя Улама. Использование природы повторов и случайностей для изучения процессов является аналогичным происходящей в казино деятельности.

При применении данного метода моделирования сначала происходит поиск вероятностного аналога. До этого моделирование осуществлялось в противоположном направлении: оно использовалось для проверки результата детерминированной проблемы, полученной ранее. И хотя и до открытия метода Монте-Карло существовали подобные подходы, они не были популярными и общими.

Энрико Ферми в 1930 году применил стохастические приемы для расчета свойств нейтрона, в то время только что обнаруженного. Методы Монте-Карло в дальнейшем использовались при работе над манхэттенским проектом, хотя в то время были существенно ограничены возможности вычислительных машин. По этой причине они получили широкое распространение только после того, как появились компьютеры.

Стохастические сигналы

Регулярные и стохастические сигналы имеют разные формы колебаний. Если повторно измерить последние, мы получим колебания, имеющие новую форму, которая отлична от предыдущей, однако проявляет определенное сходство в существенных чертах. Пример стохастического сигнала – запись колебаний волн моря.

Почему же вообще необходимо вести речь об этих достаточно необычных сигналах? Дело в том, что при изучении автоматических систем они встречаются даже чаще, чем предсказуемые.

Стохастичность и искусственный интеллект

Стохастические программы в сфере искусственного интеллекта работают с применением вероятностных методов. В качестве примера можно привести такие алгоритмы, как стохастическая оптимизация или нейронные сети. Это же относится к имитации отжига и генетическим алгоритмам. Во всех этих случаях стохастичность может содержаться в проблеме как таковой или же в планировании чего-либо в условии неопределенности. Детерминированное окружение для агента моделирования является более простым, чем стохастическое.

Итак, как мы видим, интересующее нас понятие используется во многих областях науки. Мы перечислили и охарактеризовали лишь основные сферы его применения. Изучение всех этих процессов, согласитесь, очень важно и актуально. Именно поэтому интересующее нас понятие, вероятно, будет еще долго использоваться в науке.

Источник

Элементы стохастики в начальном курсе математики

Перед современной системой образования стоит цель развития таких свойств личности, которые необходимы самой личности и обществу для включения в социально-значимую деятельность, требующую применения методов логико-вариативного мышления, основанного на законах формальной логики и обязательного оценивающего все возможные исходы наблюдаемых явлений и событий.

В соответствии с требованиями модернизации математического образования основой для формирования навыков такого мышления являются прочные логические знания (об общих приёмах мышления, используемых людьми любого профиля для осуществления своей деятельности) и стохастические знания (о закономерностях, связанных со случайными явлениями)[1].

В современной математической, методической и дидактической литературе соединение элементов теории вероятностей (лат. probabilitas – вероятность), комбинаторики (лат. combina – сочетать, соединять) математической статистики (лат. status – состояние) и некоторых других разделов математики (теория множеств, теория графов, математическая логика и др.) называется стохастикой (греч. от stochazomai – предполагать) – учением о вероятностях.

В начальном курсе математики можно говорить об использовании только отдельных элементов стохастики, что связано с возрастными и психологическими особенностями младших школьников [1]. Изучение элементов стохастики предусмотрено федеральным государственным образовательным стандартом основного общего образования второго поколения с 5-го класса.

В примерных программах по математике для начальных классов в стандартах второго поколения выделена новая содержательная линия «Работа с данными», ориентированная на развитие у обучающихся умения работать с математической информацией на основе содержания всех разделов курса математики.

Е.П.Виноградова, Н.Б.Истомина, Л.Г.Петерсон, В.Н.Рудницкая считают оправданным начинать пропедевтику элементов стохастики в начальной школе, при этом, не вводя понятий или способов решения задач, недоступных восприятию младших школьников [3].

Одним из средств формирования универсальных учебных действий младших школьников является решение стохастических задач на уроках математики. На основе работ по стохастике в начальной школе стохастические задачи определяют как класс задач, в которых результат действий однозначно не определён. Стохастические задачи формируют стохастическую культуру школьника, развивают вероятную интуицию, способствуют развитию математической грамотности [7].

Стохастические задачи можно разделить на следующие виды:

Наряду с этим, опираясь на результаты исследований Е.Е.Белокуровой, Г.В.Воробьевой, Л.В.Тарасовой, можно определить, что в начальном курсе математики стохастика базируется на следующих разделах математики:

В соответствии с данными разделами рассмотрим стохастическое содержание материала по направлениям и типовые стохастические задачи и упражнения.

Элементы стохастической содержательно-методической линии начального курса математики. Основные типовые задания

Элементы теории множеств направлены на:

— формирование у обучающихся первоначальных представлений о конечных множествах и их элементах,

— понятий «принадлежит/не принадлежит элемент множеству»,

— знакомство с основными видами множеств и способами их задания.

У обучающихся формируются следующиепредметные УУД: выполнение операций над множествами, изображение множества с помощью диаграмм Эйлера-Венна, группировка объектов по заданному свойству. При выполнении операций над множествами у обучающихся, кроме предметных умений, формируются познавательные универсальные учебные действия (самостоятельное выделение познавательной цели; поиск и выделение информации; знаково-символические действия (моделирование); смысловое чтение) и познавательные логические УУД (анализ объектов с целью выделения признаков (существенных, несущественных); построение логической цепи рассуждений; выдвижение гипотез и их обоснование).

Типовые задания

Задание 1. Продолжите фразу:

Примечание: В задании 1 о множестве говорится в явном виде.

Задание 2. Дайте названия множествам:

Задание 3. Назовите группу чисел одним словом:

а) 2; 4; 7; 9; 6 _________________.

б) 18; 25; 33; 48; 57 _______________.

в) 231; 564; 872; 954 _________________.

Элементы математической логики

Обучение решению логических задач в начальной школе включает в себя:

— понимание смысла логических связок-слов «и», «или», «не», «если …то»;

— понимание смысла кванторных слов «все», «ни один», «каждый», «некоторый»;

— построение несложных составных высказываний с вышеназванными словами и определение их истинности;

— умение проводить классификацию, сравнение, аналогию, сериацию и т.д.

Без логических операций невозможно полноценное усвоение курса математики, именно слова логических операций служат основой формирования умений решать текстовые задачи.

В процессе решения логических задач у младших школьников развиваются следующие логические УУД: построение логической цепи рассуждений, доказательств, выдвижение гипотез и их обоснование.

Типовые задания

Задание 1. Выделите 2 слова из скобок, наиболее существенные для слова, стоящего перед скобками:

Задание 2. Выпишите черты сходства – слева, а справа – черты различия названных предметов или понятий: книга – тетрадь, солнце – луна, лошадь – корова, сани – телега, линейка – треугольник, дождь – снег.

Задание 3. Аня, Женя, Нина спросили, какие оценки им поставили за контрольную работу по математике. Учитель ответил: «Плохих оценок нет. У вас троих оценки разные. У Ани не «3». У Нины не «3» и не «5». Кто какую оценку получил?

Задание 4.

1) Даны числа 1; 2; 3; 4; 5; 6; 7; 8; 9; 10. Раздели их на две группы:

2) Даны числа 2; 13; 3; 43; 6; 55; 18; 7; 9; 31. Раздели на две группы:

3) Числа 22; 35; 48; 51; 31; 45; 27; 24; 36; 20 разбиты на 2 группы: четные и нечетные. На какой строчке классификация проведена правильно?

а) 31; 35; 27; 45; 51; 22 48; 24; 20; 36.

б) 3; 35; 27; 45; 51 27; 20; 24; 36; 22; 48.

в) 27; 31; 35; 45; 51 20; 24; 22; 36; 48.

г) 26; 31; 36; 35; 45; 51 20; 24; 22; 48.

Задание 5. Какие из данных предложений истинны (верны), а какие ложны (не верны):

Источник

Статья «Стохастическая линия в школьном курсе математики.»

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Стохастическая линия в школьном курсе математики.

ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ.

На рубеже третьего тысячелетия становится очевидной универсальность вероятностно-статистических законов, они стали основой описания научной картины мира. Современная физика, химия, биология, демография, социология, лингвистика, философия, весь комплекс социально-экономических наук развиваются на вероятностно-статистической базе.

Каждый ребёнок сталкивается в своей жизни ежедневно с вероятностными ситуациями, ведь игра и азарт составляют существенную часть его жизни. Круг вопросов, связанных с осознанием соотношения понятий вероятности и достоверности, проблемой выбора наилучшего из нескольких вариантов решения, оценкой степени риска и шансов на успех, представлением о справедливости и несправедливости в играх и реальных жизненных коллизиях – всё это, несомненно, находится в сфере реальных интересов становления и развития личности.

Подготовку человека к таким проблемам во всём мире осуществляет школьный курс математики. Принципиальные решения о включении вероятностно-статистического материала как равноправной составляющей обязательного школьного математического образования приняты ныне и в нашей стране. Все перспективные государственные образовательные документы последних лет содержат вероятностно-статистическую линию в курсе математики 5-9 классов наравне с такими привычными линиями, как «Числа», «Функции», «Уравнения и неравенства», «Геометрические фигуры». Продолжение изучения этой линии ведётся и в старших классах.

В новых учебных комплектах последовательно с 5 по 9 класс проводится вероятностно-статистическая линия, органично связанная с другими темами курса. В этих учебных комплектах принят статистический подход к понятию вероятности, который методически и психологически соответствует возрастным особенностям учеников основной школы. Накопленный опыт преподавания свидетельствует о безусловной доступности этого материала, очевидном интересе, который он вызывает у учащихся, позитивном влиянии на развитие мышления школьника. Отдельные элементы вероятностно-статистического материала можно использовать на факультативах, математических кружках. Например, при решении задач широко используются вероятностные графы, что делает решения более наглядными и доступными.

В соответствии с государственными стандартами общего образования первого поколения с 2010 года в контрольные измерительные материалы по математике уже включены задания стохастической линии.

В 2011 г. уже включены в работу ЕГЭ за курс средней школы (11 класс) задания по разделу «Элементы комбинаторики, статистики и теории вероятностей».

СОДЕРЖАНИЕ МАТЕРИАЛА СТОХАСТИЧЕСКОЙ ЛИНИИ, ОБЯЗАТЕЛЬНОГО ДЛЯ ИЗУЧЕНИЯ В КУРСЕ ОСНОВНОЙ ШКОЛЫ:

понятие и примеры случайных событий;

понятия частоты события и вероятности;

равновозможные события и подсчёт их вероятности;

представление о геометрической вероятности;

представление данных в виде таблиц, диаграмм, графиков;

средние результаты измерений;

понятие о статистическом выводе на основе выборки.

Согласно требованиям государственного стандарта общего образования по математике после изучения данного раздела обучающиеся должны уметь:

находить вероятности случайных событий в простейших ситуациях;

находить частоту событий, используя собственные наблюдения и готовые статистические данные;

вычислять средние значения результатов измерений;

сравнивать шансы наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставление модели с реальной ситуацией;

понимать статистические рассуждения;

анализировать реальные числовые данные, представленные в виде диаграмм, графиков, таблиц.

В ХОДЕ ГОСУДАРСТВЕННОЙ (ИТОГОВОЙ) АТТЕСТАЦИИ ОБУЧАЮЩИХСЯ ОСНОВНОЙ ШКОЛЫ ПРЕДУСМОТРЕН КОНТРОЛЬ СЛЕДУЮЩИХ РАЗДЕЛОВ СТОХАСТИЧЕСКОЙ ЛИНИИ КУРСА МАТЕМАТИКИ:

статистические характеристики. Сбор и группировка статистических данных. Наглядное представление статистической информации: представление данных в виде таблиц, диаграмм, графиков;

комбинаторика: перебор вариантов; правило умножения. Решение комбинаторных задач путём систематического перебора возможных вариантов, а также с использованием правила умножения;

вероятность случайных событий: вычисление частоты события готовых статистических данных, нахождение вероятности случайных событий в простейших случаях.

В примерном планировании учебного материала в курсе 7 класса отводится 4 часа на «Статистические характеристики» (3 ч в неделю, всего 102 ч и 4 ч в неделю, всего 136 ч), в курсе 8 класса отводится также 4 часа на «Элементы статистики» (3 ч в неделю, всего 102 ч и 4 ч в неделю, всего 136 ч), за курс 9 класса ― 13 часов ( 3 ч в неделю, всего 102 ч) и 17 часов ( 4 ч в неделю, всего 136 ч), включая контрольную работу по данной главе, а именно : Глава V. «Элементы комбинаторики и теории вероятностей».

( Данные предоставлены для учителей, ведущих преподавание по доработанным учебникам «Алгебра, 7», «Алгебра, 8», «Алгебра, 9» авторов Ю.Н. Макарычева, Н. Г. Миндюк, К. И. Нешкова, С. Б. Суворовой под редакцией С. А. Теляковского. ) Издательство «Просвещение», 2009, с изменениями.

Среднее арифметическое, размах и мода

Медиана как статистическая характеристика

О с н о в н а я ц е л ь ― сформировать у учащихся представление о простейших статистических характеристиках и их использовании при анализе данных, полученных в результате исследования.

В 7 классе учащиеся знакомятся с такими простейшими статистическими характеристиками, как среднее арифметическое, мода, медиана, размах ряда. Учащиеся должны знать соответствующие определения, должны уметь находить эти характеристики в несложных случаях, должны понимать их практический смысл в конкретных ситуациях.

Упражнения, предлагаемые в данном параграфе, можно разделить на две группы. Первую группу составляют задания на отыскание рассматриваемых характеристик и истолкование их практического смысла. Ко второй группе относятся задания, для решения которых требуется не только знание определений изучаемых статистических характеристик, но и умение проводить необходимые рассуждения, использовать ранее введённый алгебраический аппарат. К этой группе примыкают и дополнительные упражнения.

П.9. Среднее арифметическое, размах и мода: №№167―183.

П.10. Медиана как статистическая характеристика: №№186―193.

Дополнительные упражнения к §4: №№253―257.

Рассмотрим несколько примеров из тематических тестов для подготовки к ОГЭ―2016 под редакцией Ф. Ф. Лысенко, издательство «ЛЕГИОН-М», Ростов-на-Дону, 2009.

РЕШЕНИЕ. Составим упорядоченный ряд чисел: 51, 51, 52, 53, 54, 55, 59. Мода данного ряда равна 51, так как число 51 чаще всего встречается в этом ряду. Медиана равна 53, так как упорядоченный ряд состоит из нечётного числа членов и число 53 записано посередине. Разность между модой и медианой этого ряда равна 51-53=-2.

ВАРИАНТ 1, №8. Вася в четверти получил по 12 предметам среднюю оценку 3,5. По скольким предметам он должен улучшить оценку на 1 балл, чтобы его средняя оценка стала равной 4?

РЕШЕНИЕ. Так как 3,5 – это среднее арифметическое оценок по 12 предметам, то по определению среднего арифметического имеем: =3,5, где s -сумма баллов 12 предметов. Пусть х-количество предметов, по которым он должен увеличить оценку на 1 балл, тогда х·1=х – это количество баллов, которое необходимо добавить к s , чтобы его средняя оценка стала равной 4. Получим уравнение вида: =4, + , 3,5+ 4, откуда х=6.Значит, по 6 предметам Вася должен улучшить оценку на 1 балл, чтобы его средняя оценка стала равной 4.

8 КЛАСС. §13. ЭЛЕМЕНТЫ СТАТИСТИКИ.

Сбор и группировка статистических данных

Наглядное представление статистической информации

О с н о в н а я ц е л ь ― сформировать начальные представления о сборе и обработке статистических данных, о наглядной интерпретации статистической информации.

В 8 классе учащиеся впервые встречаются с представлением результатов исследования в виде таблицы частот или относительных частот. Учащиеся должны знать соответствующие определения, должны уметь находить по таблице частот такие статистические характеристики, как среднее арифметическое, размах и мода; представлять ряд данных в виде интервального ряда, находить по данному интервальному ряду среднее значение величины, заменяя предварительно каждый интервал его серединой; строить по результатам статистических исследований полигон или гистограмму, должны понимать их практический смысл в конкретных ситуациях, так как различные виды наглядной интерпретации результатов статистических исследований постоянно встречаются в газетах и журналах, применяются для изучения различных общественных и социально-экономических явлений.

При выполнении соответствующих упражнений основное внимание следует уделить практическому смыслу этих статистических характеристик. Что касается нахождения медианы ряда данных, заданного таблицей частот, то в силу сложности этой задачи соответствующие упражнения не предлагаются. Достаточно ограничиться разбором приведённого в учебнике авторского примера.

П.40. Сбор и группировка статистических данных: №№1028-1038.

П.41. Наглядное представление статистической информации: №№1042-1056.

Дополнительные упражнения к §13: №№1092-1098.

ВАРИАНТ 8, №8. На уроке статистики ученики подсчитывали среднее значение своих четвертных оценок по математике. Для этого они составили таблицу и подсчитали среднее значение. Получилось 4,04. После урока одно число было стёрто. Восстановите его.

РЕШЕНИЕ. Обозначим отсутствующую кратность варианты через х, получаем:

4,04, 61+5х=4,04(17+х), 61+5х=68,68+4,04х, 0,96х= отсюда х=8.

9 класс. ГЛАВА V. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ.

Примеры комбинаторных задач.

О с н о в н а я ц е л ь ― ознакомить учащихся с понятиями «перестановка», «размещение», «сочетание» и соответствующими формулами, выработать умение решать несложные комбинаторные задачи.

§12. НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ.

Относительная частота случайного события.

Вероятность равновозможных событий.

Контрольная работа №8

О с н о в н а я ц е л ь ― ввести понятия «случайное событие», «относительная частота случайного события» и «вероятность случайного события» и выработать умение решать простейшие задачи с использованием этих понятий.

Учащиеся впервые знакомятся с понятием «вероятность случайного события», статистическим подходом к вычислению вероятностей, усвоению этих знаний способствуют №№791-794; классическим определением вероятности, понятиями «равновозможные исходы», «исходы, благоприятные для данного события», предлагаются №№798-806. При введении понятий «достоверное событие», «невозможное событие» и «вероятностная шкала» используются №807,№808. Специальное внимание надо уделить примеру детской игры с бросанием дротика, на котором даётся представление о геометрической вероятности(решение представлено в учебнике): №№814-816.

Материал пункта 36 «Сложение и умножение вероятностей» рассчитан на учащихся, проявляющих интерес и склонность к математике. Этот материал можно использовать для индивидуальных заданий, в кружковой работе, на факультативных занятиях.

Приведём пример контрольной работы №8 к ГЛАВЕ V по теме « ЭЛЕМЕНТЫ КОМБИНАТОРИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ».

Сколько чётных четырёхзначных чисел, в которых цифры не повторяются, можно составить с помощью цифр 1, 2, 5, 7?

Решите уравнение:

Курьер может разнести пакеты в 7 различных учреждений. Сколько маршрутов он может выбрать?

В магазине «Филателия» продаётся 8 различных наборов марок, посвящённых спортивной тематике. Сколькими способами можно выбрать из них 3 набора?

Учащиеся 3 класса изучают 10 предметов. Сколькими способами можно составить расписание на один день, чтобы в нём было 5 различных предметов?

В ящике находятся 2 белых и 3 чёрных шара. Наугад выбирается один шар. Какова вероятность того, что вынутый шар окажется белым?

7.* На координатной прямой отмечены точки А(1) и В(4). На отрезке АВ выбрана точка С(х). Какова вероятность того, что 2 3,5?

Сколько чётных четырёхзначных чисел, в которых цифры не повторяются, можно составить с помощью цифр 1, 4, 5, 8?

Решите уравнение: :

Сколько существует вариантов рассаживания вокруг стола 6 гостей на 6 стульях?

В классе 10 учеников успешно занимаются математикой. Сколькими способами можно выбрать из них 4 для участия в школьной олимпиаде?

На плоскости отметили 5 точек. Их надо обозначить латинскими буквами. Сколькими способами это можно сделать(в латинском алфавите 26 букв)?

В ящике находятся 2 белых и 3 чёрных шара. Наугад выбирается один шар. Какова вероятность того, что вынутый шар окажется чёрным?

7.* На координатной прямой отмечены точки А(-2) и В(2). На отрезке АВ выбрана точка С(х). Какова вероятность того, что 0 1,5?

Это число вида . Таких чисел столько, сколько можно составить трёхзначных чисел из цифр 1, 5, 7 (без повторения). Их 6(3!=1·2·3).

n(n+1)=72, n=8, n=9.

Количество маршрутов равно числу перестановок из 7 элементов: =7!=5040.

Выбор из 8 по 3 без учёта порядка: = = =56.

Здесь порядок выбора имеет значение, поэтому количество способов равно размещению из 10 по 5, т. е. = = =10·9·8·7·6=30240.

В ящике всего n =2+3=5 шаров; изъятие каждого из них считается равно возможным. Найдём вероятность события А – «вынут белый шар»; =2, P ( A )= = =0,4.

7*. Вероятность того, что 2 3,5 равна отношению длины отрезка |3,5-2|=1,5 к длине отрезка |4-1|=3, т. е. = =0,5.

= , =56, n=7, n=8.

Шестерых гостей можно расположить на 6 стульях =6!=720 различными способами.

Выбрать 4 человек из 10 можно способами, так как порядок выбора значения не имеет (все участники пойдут на олимпиаду как равноправные); количество способов равно числу сочетаний = = = =210.

Выбираем 5 букв для обозначения точек из 26 букв в латинском алфавите; порядок выбора имеет значение (какую точку какой буквой обозначим): = =26·25·24·23·22=7 893 600.

Ответ : 7 893 600 способов.

В ящике всего n =2+3=5 шаров; изъятие каждого из них считается равно возможным. Найдём вероятность события А – «вынут чёрный шар»; =3, P ( A )= = =0,6.