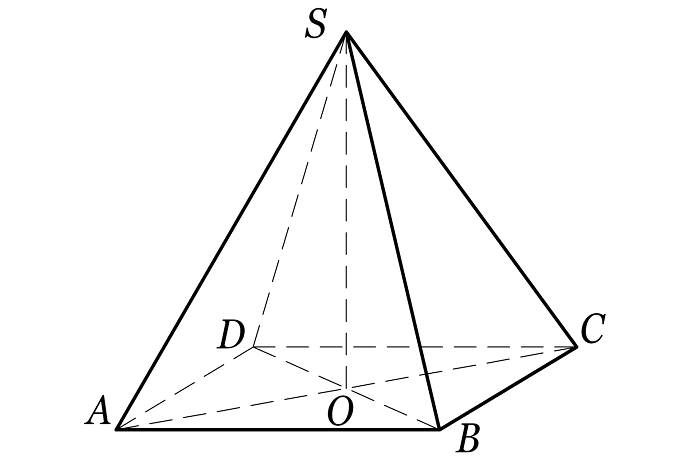
Что такое сторона пирамиды
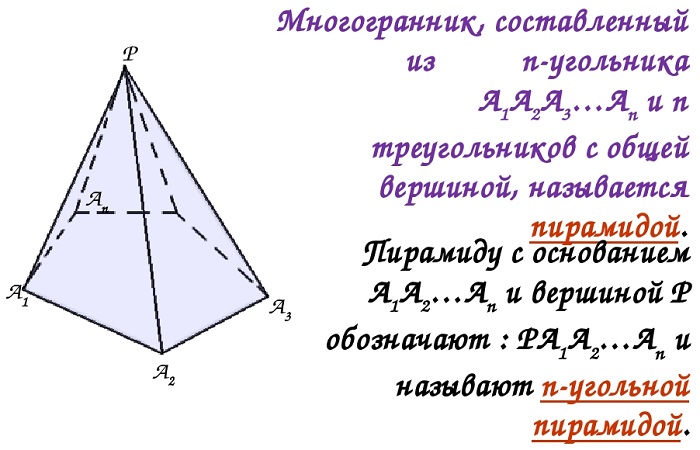
Пирамида
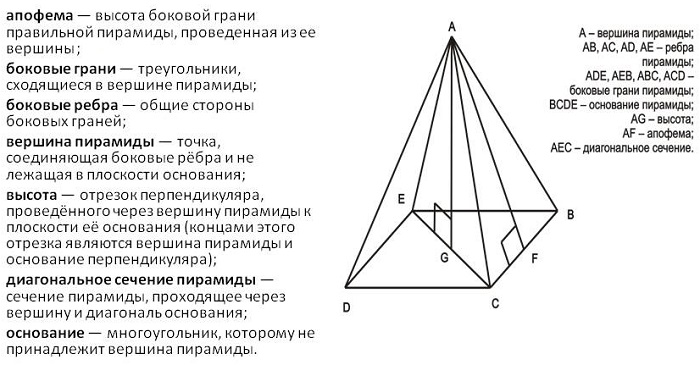
Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.
Основание — многоугольник, которому не принадлежит вершина пирамиды.
Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.
Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).
Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.
Некоторые свойства пирамиды
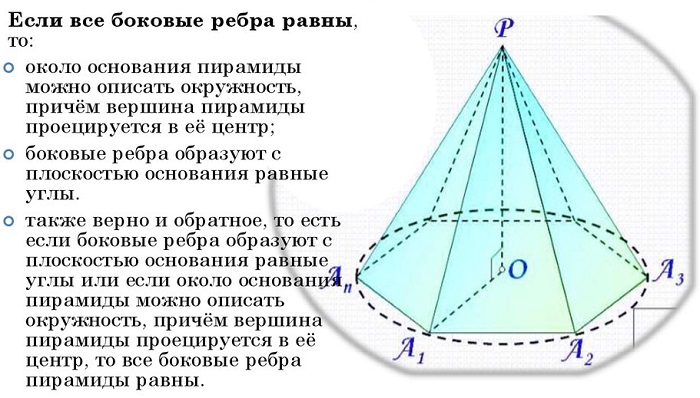
1) Если все боковые ребра равны, то
– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр
– боковые ребра образуют с плоскостью основания равные углы
Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.
Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
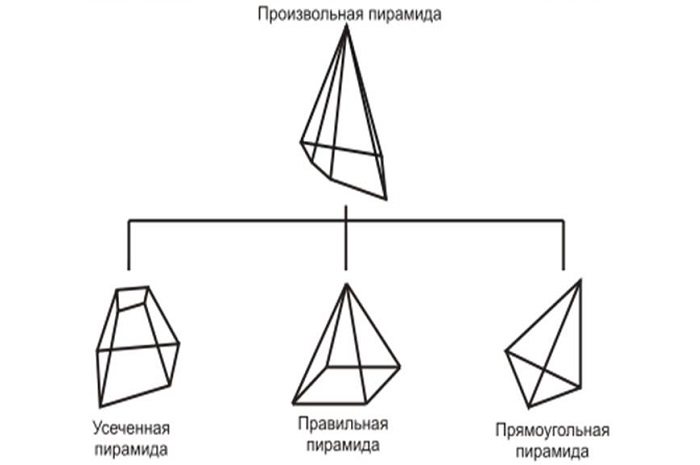
Виды пирамид
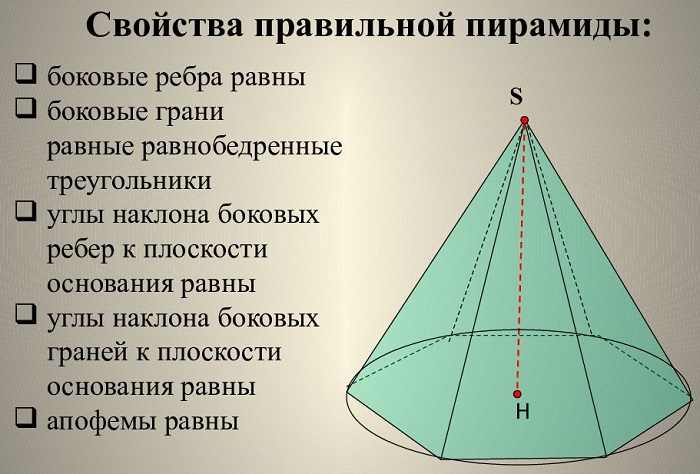
Для правильной пирамиды справедливо:
– боковые ребра правильной пирамиды равны;
– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
– в любую правильную пирамиду можно вписать сферу;
– около любой правильной пирамиды можно описать сферу;
– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.
Что такое пирамида: определение, элементы, виды, варианты сечения
В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения пирамиды. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Определение пирамиды
Пирамида – это геометрическая фигура в пространстве; многогранник, который состоит из основания и боковых граней (с общей вершиной), количество которых зависит от количества углов основания.
Примечание: пирамида – это частный случай конуса.
Элементы пирамиды
Развёртка пирамиды – фигура, полученная при “разрезе” пирамиды, т.е. при совмещении всех ее граней в плоскости одной из них. Для правильной четырехугольной пирамиды развертка в плоскости основания выглядит следующим образом.
Примечание: свойства пирамиды представлены в отдельной публикации.
Виды сечения пирамиды
1. Диагональное сечение – секущая плоскость проходит через вершину фигуры и диагональ основания. У четырехугольной пирамиды таких сечения два (по одному на каждую диагональ):
2. Если секущая плоскость параллельна основанию пирамиды, она делит ее на две фигуры: подобную пирамиду (считая от вершины) и усеченную пирамиду (считая от основания). Сечением является подобный основанию многоугольник.
Примечание: Существуют и другие виды сечения, но они не так распространены.
Геометрические фигуры. Пирамида.
Пирамида — многогранник, в основании которого лежит многоугольник, а остальные грани являются треугольниками, которые имеют общую вершину. Пирамида – это частный случай конуса.
Элементы пирамиды.
Свойства пирамиды.
1. Когда все боковые ребра имеют одинаковую величину, тогда:
2. Когда боковые грани имеют угол наклона к плоскости основания одной величины, тогда:
3. Около пирамиды можно описать сферу в том случае, если в основании пирамиды лежит многоугольник, вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы станет точка пересечения плоскостей, которые проходят через середины ребер пирамиды перпендикулярно им. Из этой теоремы делаем вывод, что как около всякой треугольной, так и около всякой правильной пирамиды можно описать сферу.
4. В пирамиду можно вписать сферу в том случае, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в 1-ной точке (необходимое и достаточное условие). Эта точка станет центром сферы.
5. Конус будет вписанным в пирамиду, когда вершины их совпадут, а основание конуса будет вписанным в основание пирамиды. При этом вписать конус в пирамиду можно лишь в том случае, если апофемы пирамиды имеют равные величины (необходимое и достаточное условие).
6. Конус будет описанным около пирамиды, если их вершины совпадут, а основание конуса будет описано около основания пирамиды. При этом описать конус около пирамиды можно лишь в том случае, если все боковые ребра пирамиды имеют одинаковые величины (необходимое и достаточное условие). Высоты у этих конусов и пирамид одинаковы.
7. Цилиндр будет вписанным в пирамиду, если 1-но его основание совпадет с окружностью, которая вписана в сечение пирамиды плоскостью, параллельной основанию, а второе основание будет принадлежать основанию пирамиды.
8. Цилиндр будет описанным около пирамиды, когда вершина пирамиды будет принадлежать его одному основанию, а второе основание цилиндра будет описано около основания пирамиды. При этом описать цилиндр около пирамиды можно лишь в том случае, если основанием пирамиды служит вписанный многоугольник (необходимое и достаточное условие).
Виды пирамид.
По количеству углов основания пирамиды делят на треугольные, четырехугольные и так далее.
Пирамида будет треугольной, четырехугольной, и так далее, когда основанием пирамиды будет треугольник, четырехугольник и так далее. Треугольная пирамида есть четырехгранник — тетраэдр. Четырехугольная — пятигранник и так далее.
Треугольная пирамида и формулы для определения ее площади
О какой пирамиде пойдет речь?
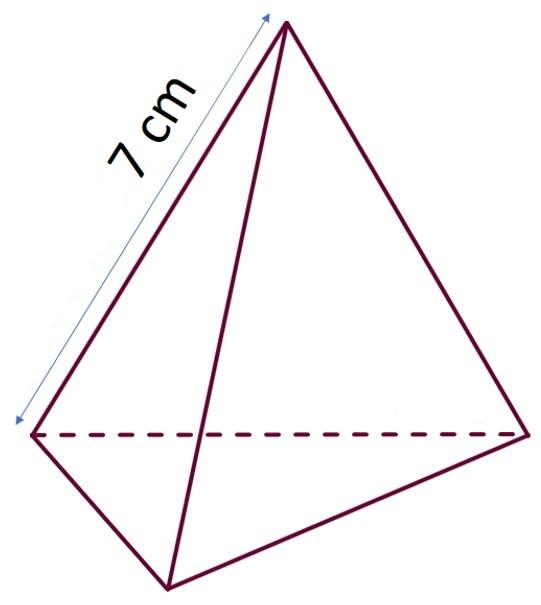
Треугольная пирамида представляет собой фигуру, которую можно получить, если соединить все вершины произвольного треугольника с одной единственной точкой, не лежащей в плоскости этого треугольника. Согласно этому определению рассматриваемая пирамида должна состоять из исходного треугольника, который называется основанием фигуры, и трех боковых треугольников, которые имеют по одной общей стороне с основанием и соединены друг с другом в точке. Последняя называется вершиной пирамиды.

Рисунок выше демонстрирует произвольную треугольную пирамиду.
Рассматриваемая фигура может быть наклонной или прямой. В последнем случае перпендикуляр, опущенный из вершины пирамиды на ее основание, должен его пересекать в геометрическом центре. Геометрическим центром любого треугольника является точка пересечения его медиан. Геометрический центр совпадает с центром масс фигуры в физике.
Если в основании прямой пирамиды будет лежать правильный (равносторонний) треугольник, то она называется правильной треугольной. В правильной пирамиде все боковые стороны равны друг другу и представляют собой равносторонние треугольники.
Если высота правильной пирамиды такова, что ее боковые треугольники становятся равносторонними, то она называется тетраэдром. В тетраэдре все четыре грани равны друг другу, поэтому каждая из них может полагаться основанием.
Элементы пирамиды
К этим элементам относятся грани или стороны фигуры, ее ребра, вершины, высота и апофемы.
Как было показано, все стороны треугольной пирамиды являются треугольниками. Их число равно 4 (3 боковых и один в основании).
Ребра можно определить, как линии пересечения двух треугольных сторон, или как линии, которые соединяют каждые две вершины. Количество ребер соответствует удвоенному числу вершин основания, то есть для треугольной пирамиды оно равно 6 (3 ребра принадлежат основанию и 3 ребра образованы боковыми гранями).
Высота, как выше было отмечено, является длиной перпендикуляра, проведенного из вершины пирамиды к ее основанию. Если из этой вершины провести высоты к каждой из сторон треугольного основания, то они будут называться апотемами (или апофемами). Таким образом, пирамида треугольная имеет одну высоту и три апофемы. Последние равны друг другу для правильной пирамиды.
Основание пирамиды и его площадь
Поскольку основание для рассматриваемой фигуры в общем случае представляет собой треугольник, то для расчета его площади достаточно найти его высоту ho и длину стороны основания a, на которую она опущена. Формула для площади So основания имеет вид:
Если треугольник основания является равносторонним, тогда площадь основания треугольной пирамиды вычисляется по такой формуле:
То есть площадь So однозначно определяется длиной стороны a треугольного основания.
Боковая и общая площадь фигуры
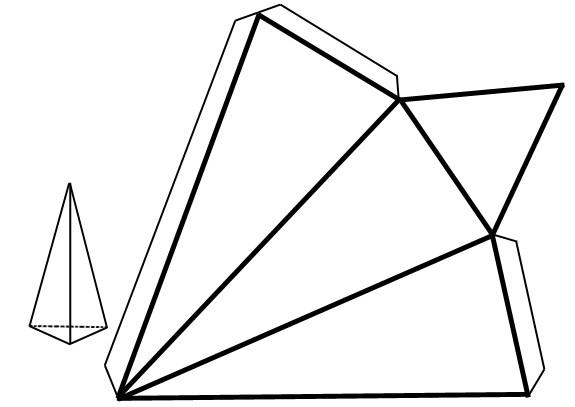
Прежде чем рассматривать площадь треугольной пирамиды, полезно привести ее развертку. Она изображена на рисунке ниже.
Площадь этой развертки, образованной четырьмя треугольниками, является общей площадью пирамиды. Один из треугольников соответствует основанию, формула для рассматриваемой величины которого была записана выше. Три боковых треугольных грани в сумме образуют боковую площадь фигуры. Поэтому для определения этой величины достаточно к каждому из них применить записанную выше формулу для произвольного треугольника, а затем, сложить три полученных результата.
Если пирамида является правильной, то расчет площади боковой поверхности облегчается, поскольку все грани боковые представляют собой одинаковые равносторонние треугольники. Обозначим hb длину апотемы, тогда площадь боковой поверхности Sb можно определить так:
Эта формула следует из общего выражения для площади треугольника. Цифра 3 появилась в числители из-за того, что пирамида имеет три боковых грани.
Апотему hb в правильной пирамиде можно вычислить, если известна высота фигуры h. Применяя теорему Пифагора, получаем:
Очевидно, что общая площадь S поверхности фигуры равна сумме ее площадей боковой поверхности и основания:
Для правильной пирамиды, подставляя все известные величины, получаем формулу:
S = √3/4*a2 + 3/2*a*√(h2 + a2/12)
Площадь пирамиды треугольной зависит только от длины стороны ее основания и от высоты.
Пример задачи
Известно, что боковое ребро треугольной пирамиды равно 7 см, а сторона основания составляет 5 см. Необходимо найти площадь поверхности фигуры, если известно, что пирамида является правильной.
Воспользуемся равенством общего вида:
So = √3/4*a2 = √3/4*52 ≈ 10,825 см2.
Для определения площади боковой поверхности, необходимо найти апотему. Не сложно показать, что через длину бокового ребра ab она определяется по формуле:
Тогда площадь Sb равна:
Sb = 3/2*a*hb = 3/2*5*6,538 = 49,035 см2.
Общая площадь пирамиды составляет:
S = So + Sb = 10,825 + 49,035 = 59,86 см2.
Заметим, что при решении задачи мы не использовали в расчетах значение высоты пирамиды.
Пирамида является одной из основных фигур в геометрии. О её особенностях рассказано в статье.
Определение пирамиды в геометрии
Эта стереометрическая фигура включает в себя часть пространства, отделённую плоскими многоугольниками: произвольным в основании и гранями — треугольниками, содержащими общую вершину и отрезок в виде общей стороны с ним.
Элементы пирамиды
Элементами этой геометрической фигуры являются:
Место, куда сходятся все боковые грани фигуры, является вершиной.
Многоугольник, от каждой стороны которого отходят треугольные грани, носит название основания. Например, оно может быть шестиугольным.
Треугольники, соединяющиеся у вершины, с общей стороной с основанием, носят название боковых граней. У них противоположная вершина совпадает с точкой вершины пирамиды.
Высота фигуры представляет собой вертикальный отрезок, ограниченный многоугольником основания и вершиной.
На каждом треугольнике боковой стороны можно указать апофему. Она опускается от вершины по грани до ребра основания, будучи к нему перпендикулярной.
Боковыми ребрами называют те отрезки, которые соединяют соседние боковые грани.
У пирамиды может быть несколько диагональных сечений. Они включают в себя диагональ многоугольника вместе с вершиной пирамиды.
Виды пирамид
Такие фигуры могут относиться к различным видам, в зависимости от типа основания и расположения вершины.
Можно указать следующие разновидности пирамид:
Правильной она будет в том случае, если в основании лежит правильный многоугольник. Проекция вершины на многоугольник основания должна приходиться на центр. Тетраэдр рассматривается как одна из разновидностей правильной пирамиды.
У прямоугольной фигуры одна из граней находится в плоскости, перпендикулярной многоугольнику, лежащему в основании.
Усеченная — это часть фигуры, находящаяся между пересекающей плоскостью и многоугольником основания. Причём эта плоскость должна располагаться горизонтально.
Свойства пирамиды
У этой объёмной геометрической фигуры имеются следующие свойства при условии равенства боковых рёбер:
круг возможно описать вокруг многоугольника основания;
угол, под которым наклонены боковые грани, будет таким же.
В том случае, когда треугольные грани имеют одни и те же углы с основанием, возможно сделать вывод о том, что их рёбра одинаковы.
Свойства правильной пирамиды
У такой фигуры можно отметить особые свойства.
У правильной пирамиды все боковые треугольники одинаковы.
Каждая из них является равнобедренным треугольником.
Внутрь любой такого типа пирамиды можно вписать сферу. При этом она будет касаться основания и всех граней, имея с каждой из этих сторон по одной общей точке.
Снаружи возможна сфера, касающаяся всех вершин.
Нетрудно вычислить площадь поверхности такой фигуры. Для этого надо умножить длину периметра многоугольника, находящегося в её основании, на половину длины апофемы.
Особым случаем является ситуация, когда у вписанной и описанной сфер центры совпадают. В этом случае можно утверждать, что если сложить все плоские углы у боковых граней, то их сумма будет равна числу «Пи». При этом, для того чтобы узнать величину каждого из них, достаточно эту величину разделить на количество граней.
Формулы объема и площади поверхности пирамиды с примерами расчета
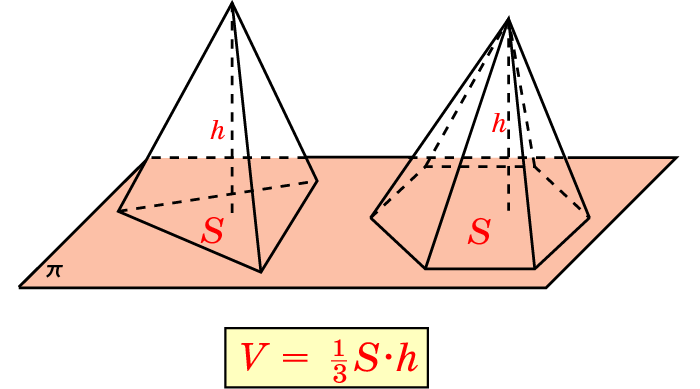
Вычислить объём можно с использованием следующей формулы.
где используются такие обозначения:
S – площадь основания;
Полную площадь поверхности можно вычислить как сумму площадей основания и всех боковых треугольников.
Пример решения задачи
Если стороны основания составляют 3 см, а боковые рёбра — 4 см, то по теореме Пифагора можно определить высоту фигуры.
Сначала по теореме Пифагора находят длину половины диагонали. Она будет равна корню квадратному из 18 (4,25 см), так как является диагональю квадрата.
Здесь рассматривается четырехугольная пирамида.
По теореме Пифагора находим высоту. Она будет равна примерно 4,5 см.
Площадь основания составляет 3 * 3 = 9 кв. см. Нужно учесть, что это квадрат со стороной 3 см. Подставив значения в формулу для объёма, получим следующее.
V = (1 / 3) * 9 * 4,5 = 13,5 куб. см.
Для расчёта площади поверхности надо узнать площадь квадратного основания и треугольных боковых сторон. Для этого сначала по теореме Пифагора находят длину апофемы. Она будет равна 4,27 см.
Каждая боковая сторона имеет площадь 12,81 кв. см, а основание — 9 кв. см. Сложив площади всех граней, получим 60,24 кв. см. Посчитать площадь поверхности можно, рассмотрев развертку фигуры.