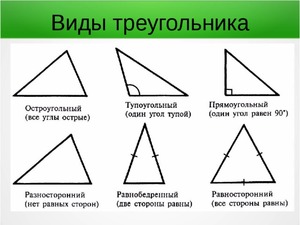
Что такое стороны многоугольника 8 класс определение

Многоугольник

Определение 1. Многоугольник − замкнутая ломаная линия.

Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:

Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.

Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.

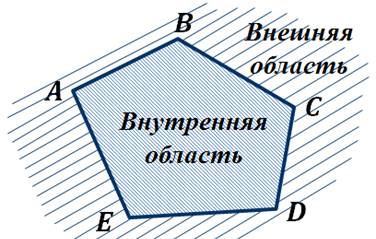
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.

Виды многоугольников

Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с \( \small n \) вершинами называется \( \small n- \)угольником.

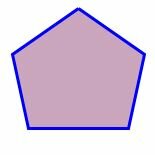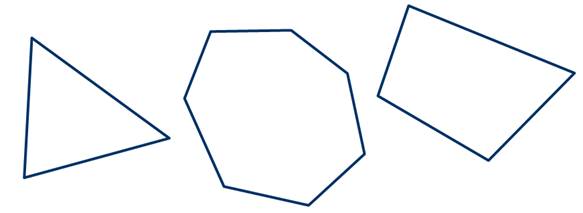
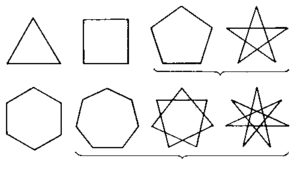
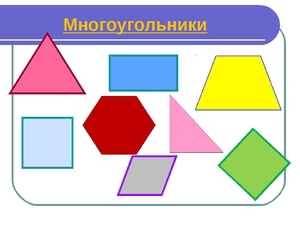
На рисунке 1 представлены различные виды многоугольников.

Обозначение многоугольника

Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют \( \small A_1A_2A_3A_4A_5A_6 \) или \( \small A_6A_5A_4A_3A_2A_1 \).

Соседние вершины многоугольника

Вершины многоугольника называются соседними, если они являются концами одной из его сторон.

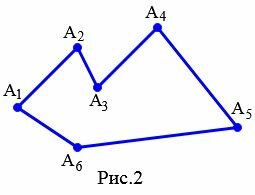На рисунке 2 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)

Смежные стороны многоугольника

Стороны многоугольника называются смежными, если они имеют общую вершину.

На рисунке 2 стороны \( \small A_4A_5 \) и \( \small A_5A_6 \) являются смежными, так как они имеют общую вершину \( \small A_5. \)

Простой многоугольник. Самопересекающийся многоугольник

Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).

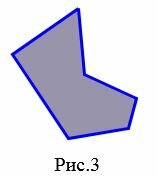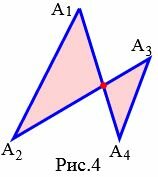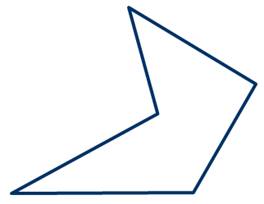
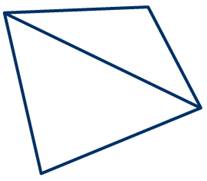
На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой многоугольник называется самопересекающийся многоугольник.

Выпуклый многоугольник

Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.

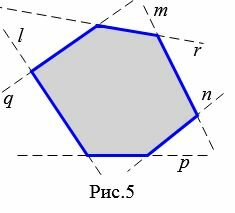На рисунке 5 многоугольник лежит по одну сторону от прямых \( \small m, \ n, \ l, \ p, \ q, \ r\) проходящих через стороны многоугольника.

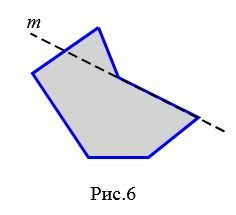На рисунке 6 прямая \( \small m\) делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой \( \small m\). Следовательно многоугольник не является выпуклым.

Правильный многоугольник

Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.

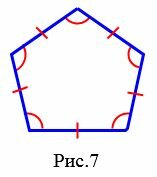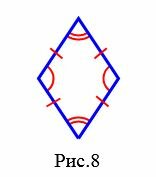На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.

Звездчатый многоугольник

Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.

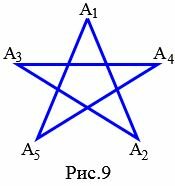На рисунке 9 представлен звездчатый пятиугольник поскольку все углы \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) равны и равны все стороны: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)

Периметр многоугольника

Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника \( \small A_1A_2. A_A_n \) периметр вычисляется из формулы:

Угол многоугольника

Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small A_3 \) на рисунке 2).

Внешний угол многоугольника

Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.

На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине \( \small E. \)

Диагональ многоугольника. Количество диагоналей

Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.

Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:

Сумма углов выпуклого многоугольника

Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины \( \small A_1 \) все диагноали многоугольника \( \small A_1A_2. A_A_n \) (Рис.11):

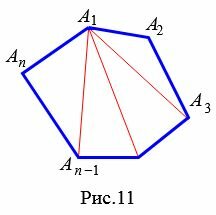Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно \( \small n-3 \). Следовательно, эти диагонали разделяют многоугольник на \( \small n-3+1=n-2 \) треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: \( \small 180°(n-2). \)

где \( \small n \) −количество сторон (вершин) выпуклого многоугольника.

Угол правильного многоугольника

Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:

где \( \small n \) −количество сторон (вершин) правильного многоугольника.

Источник

Многоугольники

Многоугольник — это геометрическая фигура, ограниченная замкнутой ломаной линией, не имеющей самопересечений.

Звенья ломаной называются сторонами многоугольника, а её вершины — вершинами многоугольника.

Углами многоугольника называются внутренние углы, образованные соседними сторонами. Число углов многоугольника равно числу его вершин и сторон.

Многоугольникам даются названия по количеству сторон. Многоугольник с наименьшим количеством сторон называется треугольником, он имеет всего три стороны. Многоугольник с четырьмя сторонами называется четырёхугольником, с пятью — пятиугольником и т. д.

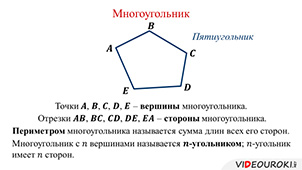
Обозначение многоугольника составляют из букв, стоящих при его вершинах, называя их по порядку (по часовой или против часовой стрелки). Например, говорят или пишут: пятиугольник ABCDE :

В пятиугольнике ABCDE точки A, B, C, D и E — это вершины пятиугольника, а отрезки AB, BC, CD, DE и EA — стороны пятиугольника.

Выпуклые и вогнутые

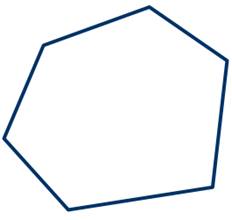
Многоугольник называется выпуклым, если ни одна из его сторон, продолженная до прямой линии, его не пересекает. В обратном случае многоугольник называется вогнутым:

Периметр

Сумма длин всех сторон многоугольника называется его периметром.

Периметр многоугольника ABCDE равен:

Если у многоугольника равны все стороны и все углы, то его называют правильным. Правильными многоугольниками могут быть только выпуклые многоугольники.

Диагональ

Диагональ многоугольника — это отрезок, соединяющий вершины двух углов, не имеющих общей стороны. Например, отрезок AD является диагональю:

Единственным многоугольником, который не имеет ни одной диагонали, является треугольник, так как в нём нет углов, не имеющих общих сторон.

Если из какой-нибудь вершины многоугольника провести все возможные диагонали, то они разделят многоугольник на треугольники:

Треугольников будет ровно на два меньше, чем сторон:

где t — это количество треугольников, а n — количество сторон.

Разделение многоугольника на треугольники с помощью диагоналей используется для нахождения площади многоугольника, так как чтобы найти площадь какого-нибудь многоугольника, нужно разбить его на треугольники, найти площадь этих треугольников и полученные результаты сложить.

Источник

Многоугольник

Урок 1. Геометрия 8 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Многоугольник»

На этом уроке мы поговорим о геометрической фигуре, которую называют многоугольником. Уже само слово «многоугольник» указывает на то, что эта фигура имеет много углов.

Давайте посмотрим на следующую фигуру, которая составлена из отрезков AB, BC, CD, DE, EA. Причем смежные отрезки, то есть отрезки AB и BC, BC И CD, CD и DЕ, DE и ЕА, ЕА и АB не лежат на одной прямой, а несмежные отрезки, например, AB и CD, BC и ED, АЕ и CD, не имеют общих точек. Такую фигуру называют многоугольником.

Точки A, B, C, D и Е называются вершинами этого многоугольника, а отрезки AB, BC, CD, DE и ЕА – его сторонами.

Периметром многоугольника называется сумма длин всех его сторон.

Обратите внимание, что рассматриваемый многоугольник имеет 5 вершин и 5 сторон, а поэтому его называют пятиугольником.

Многоугольник с n вершинами называется n-угольником. N-угольник имеет n сторон.

Треугольник является примером многоугольника. Четырёхугольник и семиугольник также являются примерами многоугольников.

А вот следующая фигура не является многоугольником, так как несмежные отрезки и имеют общую точку.

Вернёмся к многоугольнику, рассматриваемому вначале урока.

А вот отрезок, соединяющий любые две не соседние вершины, например, AC, BЕ, АD, называется диагональю многоугольника.

Многоугольник разделяет плоскость на две части, а именно, на внутреннюю область многоугольника и на внешнюю.

Следует отметить, что многоугольником также называют фигуру, состоящую из отрезков и внутренней области.

Все многоугольники делят на выпуклые и невыпуклые. Многоугольник называется выпуклым, если он лежит по одну сторону от прямой, проходящей через любые две соседние вершины.

А вот если многоугольник лежит по разные стороны хотя бы от одной прямой, проходящей через две соседние вершины, то его называют невыпуклым.

Теперь давайте выясним, чему же равна сумма углов выпуклого n-угольника.

Давайте возьмём выпуклый четырёхугольник и проведём в нем диагональ, Получили два треугольника.

Мы знаем, что сумма углов треугольника равна ста восьмидесяти градусам. А тогда сумма углов выпуклого четырёхугольника равняется сумме углов этих двух треугольников, то есть равняется 180º умножить на 2 и равняется 360º.

Теперь возьмем выпуклый пятиугольник и, проведя в нём две диагонали, разобьём его на три треугольника.

Тогда сумма углов выпуклого пятиугольника равняется .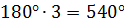

И возьмем еще, например, выпуклый шестиугольник. Проведём в нем три диагонали.

И получим четыре треугольника. А тогда сумма углов выпуклого шестиугольника будет равна .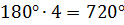

Таким образом, мы могли бы продолжать находить суммы углов других выпуклых многоугольников. Но обратите внимание, что в четырёхугольнике четыре стороны и мы его разбили на два треугольника. В пятиугольнике: пять сторон – три треугольника. А в шестиугольнике: шесть сторон – четыре треугольника

То есть в каждом случае получается, что треугольников на два меньше, чем сторон у рассматриваемой фигуры.

На основании этого сделаем вывод: сумма углов выпуклого n-угольника равна 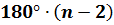, где n – количество сторон (углов).

А теперь давайте решим несколько задач.

Задача. Найти сумму углов выпуклого: а) пятиугольника; б) десятиугольника.

Для того чтобы найти сумму углов выпуклого пятиугольника, мы в полученное выше выражение вместо n подставим 5, выполним вычисления и получим 540º.

а) ;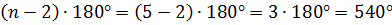

А вот чтобы найти сумму углов десятиугольника, подставим в выражение вместо n 10:

б) .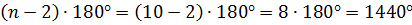

Ответ: 540 градусов, 1440 градусов.

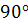
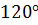
Задача. Сколько сторон имеет выпуклый многоугольник, каждый угол которого равен: а) ; б) ?

Источник

Геометрическая фигура многоугольник

Многоугольником называется геометрическая фигура, которая со всех сторон ограничена замкнутой ломаной линией. При этом количество звеньев ломаной не должно быть меньше трех. Каждая пара отрезков ломаной имеет общую точку и образует углы. Количество углов совместно с количеством отрезков ломаной являются основными характеристиками многоугольника. В каждом многоугольнике количество звеньев ограничивающей замкнутой ломаной совпадает с количеством углов.

Сторонами в геометрии принято называть звенья ломаной линии, которая ограничивает геометрический объект. Вершинами называют точки соприкосновения двух соседних сторон, по количеству которых получают свои названия многоугольники.

Если замкнутая ломаная состоит из трех отрезков, она носит название треугольника; соответственно, из четырех отрезков — четырехугольником, из пяти — пятиугольником и пр.

Для обозначения треугольника или четырехугольника пользуются заглавными латинскими буквами, обозначающими его вершины. Буквы называют по порядку — по часовой стрелке или против нее.

Основные понятия

Описывая определение многоугольника, следует учитывать некоторые смежные геометрические понятия:

Как уже упоминалось выше, названия многоугольных геометрических строятся исходя из количества вершин. Если у фигуры их количество равняется n, она носит название n-угольника:

Любой выпуклый n-угольник можно поделить на треугольники. При этом количество треугольников бывает меньше количества сторон на 2.

Виды фигур

Треугольник

Это многоугольник с тремя вершинами и тремя отрезками, соединяющими их. При этом точки соединения отрезков не лежат на одной прямой.

Точки соединения отрезков — это вершины треугольника. Сами отрезки называются сторонами треугольника. Общая сумма внутренних углов каждого треугольника равняется 180°.

По соотношениям между сторонами все треугольники можно подразделять на несколько видов:

Кроме того, принято различать следующие треугольники:

Четырехугольник

Четырехугольником называется плоская фигура, имеющая 4 вершины и 4 отрезка, которые их последовательно соединяют.

На одной прямой не может находиться сразу три вершины четырехугольника.

Видео

Дополнительную информацию о многоугольниках вы найдете в этом видео.

» width=»560″ height=»314″ allowfullscreen=»allowfullscreen»>

Источник

Вершины многоугольника называются соседними, если они являются концами одной из его сторон. Отрезки, соединяющие не соседние вершины многоугольника, называются диагоналями.

Многоугольник называется выпуклым если:

Определение I — для любых двух точек внутри него соединяющий их отрезок полностью лежит в нём.

Определение II — каждый внутренний угол меньше 180°.

Определение III — все его диагонали полностью лежат внутри него.

Определение IV – он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.

Сумма углов выпуклого n-угольника равна (n-2)∙180°.

Сумма углов невыпуклого n-угольника также равна (n-2)∙180°. (Доказательство аналогично, но использует в дополнение лемму о том, что любой многоугольник может быть разрезан диагоналями на треугольники).

Теорема: Число диагоналей всякого n-угольника равно .

Задача*: в каком выпуклом многоугольнике диагоналей на 25 больше чем сторон?

р = 25+n
25+n =

Разложим на множители

(n+5)(n-10)=0
n=-5 не удовлетворяет,

так как не существует

n = 10 удовлетворяет
Ответ: Десяти угольник.

Фигуры с равными диагоналями.*

Каждый четырехугольник имеет четыре вершины, четыре стороны и две диагонали.

Две несмежные стороны называются противоположными.

Две не соседние вершины называются противоположными.

1) Противоположные стороны параллелограмма равны. AB=DC, AD=BC.

2) Противоположные углы параллелограмма равны. ÐA=ÐC, ÐB=ÐD.

3) Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. AO=OC, BO=OD.

4) Сумма углов, прилежащих к одной стороне, равна 180°. ÐA+ÐD=180°, ÐA+ÐB=180°, ÐB+ÐC=180°, ÐD+ÐC=180°.

5) Сумма всех углов равна 360°. ÐA+ÐB+ÐC+ÐD=360°.

6)* Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: AC2+BD2=2∙(AB2+AD2).

Задача 1*: Найти диагональ параллелограмма, если известно, что длина одной диагонали равна AC=9 см, а стороны AD=7 см и AB=4 см.

Решение: Подставив значения в формулу получим:

BD2=49, следовательно вторая диагональ равна BD=7 см. Ответ: 7 см.

Задача 2*: Найти диагональ параллелограмма, если известно, что длина одной диагонали равна BD=10 см, а стороны AD=8 см и AB=2 см.

Решение: Условия задачи не верно, так как сумма двух сторон треугольника всегда больше третей стороны. Ответ: задача не имеет решений (смысла).

Задача 3*: а)Найти сторону параллелограмма, если известно, что длина диагоналей равна BD=6 см, AC=8, а одна сторона AB=5 см. б)Как называется этот параллелограмм.

Задача 4**: Сумма длин диагоналей параллелограмма равна 12 см, а произведение 32 найдите значение суммы квадратов всех его сторон.

Задача 5**:Найдите наибольший периметр параллелограмма, диагонали которого 6 см и 8 см.

Решение: Докажем, что среди всех параллелограммов с данными длинами диагоналей наибольший периметр имеет ромб.

Действительно, пусть a и b – длины соседних сторон параллелограмма, а и – длины его диагоналей (см. рис. 2). Тогда периметр параллелограмма: P = 2(a + b).

Из равенства , выражающего теорему о сумме квадратов диагоналей параллелограмма, следует, что у всех параллелограммов с данными диагоналями сумма квадратов сторон есть величина постоянная.

По неравенству между средним арифметическим и средним квадратичным: Û , причем равенство достигается т. и т. т., когда a = b. Значит, параллелограмм с наибольшим периметром является ромбом. Находим сторону этого ромба: =5(см). Ответ: 20 см.

Определение 2: это четырёхугольник, у которого все углы прямые.

Определение 3: это параллелограмм, у которого один угол прямой.

Свойства прямоугольника: те же свойства, что и у параллелограмма +

1) Диагонали прямоугольника равны.

2)* Квадрат диагонали равен сумме квадратов сторон.

Задача 1: Меньшая сторона прямоугольника равна 5см, диагонали пересекаются под углом 60°. Найдите диагонали прямоугольника.

Задача 2: Меньшая сторона прямоугольника равна 24, диагонали пересекаются под углом 120°. Найдите диагонали и большую сторону прямоугольника.

Задача 3*: Сторона прямоугольника равна 3 см, диагональ 5 см. Найдите другую сторону прямоугольника.

Задача 4*: Сторона прямоугольника равна 6 см, диагональ 10 см. Найдите площадь прямоугольника.

Определение 2: это четырёхугольник, у которого все стороны равны.

Свойства ромба: те же свойства, что и у параллелограмма +

1) Диагонали ромба взаимно перпендикулярны (AC ⊥ BD).

3)*Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма).

Задача 1: Диагонали ромба 6 и 8 см. Найти сторону ромба.

Задача 2: Сторона ромба 10 см, один из углов 60°. Найти маленькую диагональ ромба.

Источник