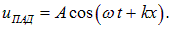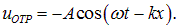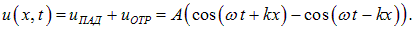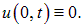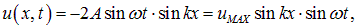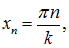Что такое стоячая волна как она образуется

Что такое стоячая волна как она образуется

Если в среде распространяется несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Волны накладываются друг на друга, не возмущая (не искажая друг друга). Это и есть принцип суперпозиции волн.

Если две волны, приходящие в какую-либо точку пространства, обладают постоянной разностью фаз, такие волны называются когерентными. При сложении когерентных волн возникает явление интерференции.

Очень важный случай интерференции наблюдается при наложении двух встречных плоских волн с одинаковой амплитудой. Возникающий в результате колебательный процесс называется стоячей волной. Практически стоячие волны возникают при отражении от преград.

Напишем уравнения двух плоских волн, распространяющихся в противоположных направлениях (начальная фаза ):

Сложим уравнения и преобразуем по формуле суммы косинусов (5.4.3):

.

Т.к. , то можно записать:

.

Учитывая, что , получим уравнение стоячей волны:

В выражении для фазы не входит координата, поэтому можно записать:

где суммарная амплитуда .

В точках, где координаты удовлетворяют условию (n = 1, 2, 3, …), , суммарная амплитуда равна максимальному значению: , – это пучности стоячей волны. Координаты пучностей:

В точках, координаты которых удовлетворяют условию (n = 0, 1, 2,…), и суммарная амплитуда колебаний равна нулю , – это узлы стоячей волны. Координаты узлов:

Точки среды, находящиеся в узлах, колебаний не совершают.

Образование стоячих волн наблюдают при интерференции бегущей и отраженных волн. На границе, где происходит отражение волны, получается пучность, если среда, от которой происходит отражение, менее плотная (рис. 5.5, а), и узел – если более плотная (рис. 5.5, б).

Если рассматривать бегущую волну, то в направлении ее распространения переносится энергия колебательного движения. В случае же стоячей волны переноса энергии нет, т.к. падающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях.

Источник

2.4. Стоячие волны

Помимо бегущих волн предыдущего раздела, в природе существуют и стоячие волны, образующиеся в результате суперпозиции бегущих. Мы постоянно встречаемся с ними в своей практической жизни: когда говорим, поем, слушаем музыку. В этом разделе, после общих математических формул, мы совсем коротко обсуждаем некоторые вопросы музыкальной акустики – в надежде, что эта часть не покажется нашим студентам самой скучной.

Струна, закрепленная на одном конце

Предположим, что струна закреплена неподвижно в точке с координатой 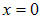и тянется в положительном направлении оси х. Пусть по струне справа налево (то есть в отрицательном направлении оси х) распространяется волна

Дойдя до точки закрепления, волна отразится. Если пренебречь потерями энергии, то амплитуда отраженной волны совпадет с амплитудой падающей волны. Надо учесть также, что при отражении происходит изменение направления движения элемента на обратное (как в упругом ударе шарика о стенку):

Суперпозиция падающей и отраженной волн имеет вид:

Мы видим, что в любой момент времени

Это и есть условие закрепления струны в точке 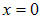. Воспользовавшись известными формулами тригонометрии для преобразования разности косинусов, записываем (2.53) в виде:

где 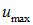— наибольшее смещение в стоячей волне.

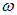
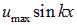
Мы нашли особый тип колебаний: в каждой точке пространства струна колеблется с частотой и амплитудой , причем все точки струны одновременно достигают своих максимальных отклонений (или проходят положение равновесия), и если мы находимся, например, в узле струны, то есть в точке с координатой

то в любой момент времени эта точка остается узлом. Иными словами, здесь нет движения волны, точки узлов волны (нулевых значений смещения) неподвижны, равно как и точки ее максимумов. Такие колебания и называются стоячими волнами.

Стоячая волна — периодическое колебание с характерным пространственным распределением амплитуды – чередованием узлов (нулей) и пучностей (максимумов). В одномерных (линейных) системах может быть представлена как сумма двух бегущих волн, распространяющихся навстречу друг другу.

В стоячей волне плотность энергии меняется от точки к точке и зависит от времени, но в отличие от бегущей волны, здесь нет переноса энергии.

Это очевидно хотя бы потому, что точки узлов волны неподвижны, и переноса энергии через них быть не может. Можно рассуждать и иначе: две бегущие волны, образовавшие стоячую, переносят одну и ту же энергию, но в противоположных направлениях, так что оба эти процесса взаимно компенсируются.

На рис. 2.9 показано образование стоячей волны при сложении двух бегущих навстречу друг другу монохроматических волн.

Рис. 2.9. Возникновение стоячей волны

Подставляя найденное решение (2.53) в выражение (2.39), получаем для мгновенного значения плотности энергии стоячей волны выражение

Источник

Стоячая волна

Из Википедии — свободной энциклопедии

Стоячая волна — колебательный (волновой) процесс в распределённых колебательных системах с характерным устойчивым в пространстве расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Такой колебательный процесс возникает при интерференции нескольких когерентных волн.

Например, стоячая волна возникает при отражении волны от преград и неоднородностей в результате взаимодействия (интерференции) падающей и отражённой волн. На результат интерференции влияют частота колебаний, модуль и фаза коэффициента отражения, направления распространения падающей и отражённой волн друг относительно друга, изменение или сохранение поляризации волн при отражении, коэффициент затухания волн в среде распространения. Строго говоря, стоячая волна может существовать только при отсутствии потерь в среде распространения (или в активной среде) и полном отражении падающей волны. В реальной же среде наблюдается режим смешанных волн, поскольку всегда присутствует перенос энергии к местам поглощения и излучения. Если при падении волны происходит её полное поглощение, то отражённая волна отсутствует, интерференции волн нет, амплитуда волнового процесса в пространстве постоянна. Такой волновой процесс называют бегущей волной.

Примерами стоячей волны могут служить колебания струны, колебания воздуха в органной трубе [3] ; в природе — волны Шумана. Для демонстрации стоячих волн в газе используют трубу Рубенса.

Источник

Что такое стоячая волна? Что такое стоячая волна? Как она возникает? В чем отличие стоячей волны от бегущей?

Стоя́чая волна́ — колебания в распределенных колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения.

Примерами стоячей волны могут служить колебания струны, колебания воздуха в органной трубе; в природе — волны Шумана.

Чисто стоячая волна, строго говоря, может существовать только при отсутствии потерь в среде и полном отражении волн от границы. Обычно, кроме стоячих волн, в среде присутствуют и бегущие волны, подводящие энергию к местам её поглощения или излучения.

Для демонстрации стоячих волн в газе используют трубу Рубенса.

Всякий волновой процесс, связанный с распространением возмущений, может сопровождаться образованием С. в. Они могут возникать не только в газообразных, жидких и твёрдых средах, но также и в вакууме при распространении и отражении электромагнитных возмущений, например в электрических длинных линиях. Антенна радиопередатчика часто выполняется в виде прямолинейного вибратора или системы вибраторов, по длине которых устанавливается С. в. В отрезках волноводов и замкнутых объёмах различной формы, используемых в качестве резонаторов в технике сверхвысоких частот, устанавливаются С. в. определённых типов. В электромагнитных С. в. электрические и магнитные поля разделяются аналогично тому, как в упругих С. в. разделяются смещение и давление.

В оптике также возможно установление С. в. с видимыми максимумами и минимумами электрического поля. Если свет не монохроматический, то в С. в. пучности электрического поля разных длин волн будут расположены в разных местах и нередко наблюдается разделение цветов.

Налейте воды в ванну и пошлепайте рукой по поверхности. От руки будут разбегаться волны во все стороны. Они называются бегущие. Плавно изменяя частоту колебаний руки Вы можете добиться того, чтобы волны перестали перемещаться в стороны, а оставались на месте. Движение происходило бы только вверх и вниз. Это и есть стоячие волны.

Образуются они в данном случае только потому, что ванна имеет стенки, от которых происходит отражение, если бы стенок не было, то стоячие волны бы не образовались, как например, на открытой водной поверхности.

Объяснение возникновения стоячих волн простое, при сталкивании прямой волны и волны, отраженной от стенки, они усиливают друг друга, и если это сталкивание происходит все время в одном и том же месте, то исчезает горизонтальное перемещение волн.

Источник

Стоячие волны: формулы, характеристики, виды, примеры

Содержание:

В стоячие волны Это волны, которые распространяются в ограниченной среде, движутся и приходят в части пространства, в отличие от бегущих волн, которые при распространении удаляются от источника, который их породил, и не возвращаются к нему.

Они являются основой звуков, производимых музыкальными инструментами, поскольку легко возникают в закрепленных струнах либо на одном, либо на обоих концах. Они также создаются на плотных мембранах, таких как барабаны, или внутри труб и конструкций, таких как мосты и здания.

Когда у вас есть фиксированная струна на обоих концах, например, у гитары, создаются волны с одинаковой амплитудой и частотой, которые распространяются в противоположных направлениях и объединяются, создавая явление, называемое вмешательство.

Если волны синфазны, пики и впадины выровнены и в результате получается волна с удвоенной амплитудой. В таком случае мы говорим о конструктивном вмешательстве.

Но если мешающие волны не совпадают по фазе, пики одной встречаются с впадинами других, и результирующая амплитуда равна нулю. Тогда речь идет о деструктивном вмешательстве.

Формулы и уравнения

Основными элементами волны, представляющей ее в пространстве и времени, являются ее амплитуда A, длина волны λ и угловая частота ω.

В математическом представлении предпочтительнее использовать k, чем волновое число или количество раз, когда волна встречается на единицу длины. Поэтому он определяется длиной волны λ, которая представляет собой расстояние между двумя долинами или двумя гребнями:

В то время угловая частота относится к периоду или продолжительности полного колебания, например:

А также частота f определяется как:

Также волны движутся со скоростью v в соответствии:

Математическое выражение стоячей волны

Математически мы можем выразить волну синусоидальной функцией или косинусоидальной функцией. Предположим, что у нас есть волны одинаковой амплитуды A, длины волны λ и частоты ω, распространяющиеся вдоль струны и в противоположных направлениях:

При их добавлении находим получившуюся волну и_р:

Чтобы найти сумму, существует тригонометрическое тождество:

По этому тождеству результирующая волна y_р осталось:

Y_р = [2A sin kx]. cos ωt

Расположение узлов и брюшков

Результирующая волна имеет амплитуду A_р = 2Asen kx, который зависит от положения частицы. Тогда в точках, для которых sin kx = 0, амплитуда волны обращается в нуль, т. Е. Отсутствует вибрация.

Поскольку k = 2 π / λ:

В таких местах происходит деструктивная интерференция, которая называется узлы. Они разделены расстоянием, равным λ / 2, как следует из предыдущего результата.

А между двумя последовательными узлами находятся пучности или животы, в котором амплитуда волны максимальна, так как там происходит конструктивная интерференция. Они возникают при:

kx = ± π / 2, 3π / 2, 5π / 2…

Снова k = 2 π / λ и тогда:

x = λ / 4, 3λ / 4, 5λ / 4,…

Нормальные режимы на струне

Граничные условия в струне определяют, каковы длины волн и частоты. Если струна длины L закреплена на обоих концах, она не может вибрировать ни на какой частоте, потому что точки, в которых закреплена струна, уже являются узлами.

Кроме того, расстояние между соседними узлами составляет λ / 2, а между узлом и животом λ / 4, таким образом, только для определенных длин волн создаются стационарные волны: те, в которых целое число n из λ / 2 помещается в из:

(λ / 2) = L, где n = 1, 2, 3, 4….

Гармоники

Различные значения, которые принимает λ, называются гармоники. Таким образом, мы имеем:

-Первая гармоника: λ = 2L

-Вторая гармоника: λ = L

-Третья гармоника: λ = 2 L / 3

-Четвертая гармоника: λ = L / 2

Скорость и частота

Хотя кажется, что стоячая волна не движется, уравнение остается в силе:

Теперь можно показать, что скорость, с которой волна распространяется в струне, зависит от натяжения T в ней и ее линейной плотности массы μ (массы на единицу длины) как:

Характеристики стоячих волн

-Когда волны неподвижны, результирующая волна не распространяется так же, как ее компоненты, которые переходят из одной стороны в другую. Есть точки, где y = 0, потому что нет вибрации: узлы, другими словами, амплитуда A_р он становится нулевым.

-Математическое выражение стоячей волны состоит из произведения пространственной части (которая зависит от координаты x или пространственных координат) и временной части.

-Между узлами результирующая черная волна колеблется в одном месте, в то время как волны, которые переходят из одной стороны в другую, не совпадают по фазе там.

-Энергия не переносится точно в узлах, так как она пропорциональна квадрату амплитуды, но задерживается между узлами.

-Расстояние между соседними узлами составляет половину длины волны.

-Точки, в которых закреплена веревка, также считаются узлами.

Типы

Стоячие волны в одном измерении

Стоячие волны в двух и трех измерениях

Стоячие волны также могут быть представлены в двух и трех измерениях, поскольку их математическое описание немного сложнее.

Примеры стоячих волн

Фиксированные веревки

— Фиксированный трос на одном конце, который колеблется вручную или с помощью поршня на другом, генерирует стоячие волны по всей своей длине.

Музыкальные инструменты

-При игре на струнных инструментах, таких как гитара, арфа, скрипка и фортепиано, также возникают стоячие волны, так как струны имеют разное натяжение и закреплены на обоих концах.

Стоячие волны также создаются в трубках с воздухом, например в органах.

Здания и мосты

Стоячие волны возникают в таких конструкциях, как мосты и здания. Примечательным случаем стал подвесной мост Tacoma Narrows около города Сиэтл, США. Вскоре после открытия в 1940 году этот мост рухнул из-за стоячих волн, созданных ветром внутри.

Частота ветра была соединена с собственной частотой моста, создавая в нем стоячие волны, амплитуда которых увеличивалась, пока мост не рухнул. Это явление известно как резонанс.

Сейш

В портах есть очень любопытное явление под названием сейша, в котором морские волны производят большие колебания. Это связано с тем, что воды в порту довольно замкнутые, хотя океанические воды время от времени проникают через вход в порт.

Воды порта движутся со своей частотой, как и воды океана. Если обе воды равны по своим частотам, большая стоячая волна создается резонансом, как это произошло с мостом Такома.

В сейши Они также могут встречаться в озерах, водохранилищах, бассейнах и других водоемах с ограниченной поверхностью.

Аквариумы

Стоячие волны могут возникать в аквариуме, который несет человек, если частота, с которой человек ходит, равна частоте колебаний воды.

Упражнение решено

Струна гитары имеет L = 0,9 м и линейную массовую плотность μ = 0,005 кг / м. Он подвергается натяжению 72 Н, и его режим колебаний соответствует показанному на рисунке, с амплитудой 2А = 0,5 см.

а) Скорость распространения

в) Соответствующее уравнение стоячей волны.

Решение для

v = [72 Н / (0,005 кг / м)] 1/2 = 120 м / с.

Решение б

Расстояние между двумя соседними узлами λ / 2, поэтому:

λ = 2L / 3 = 2 x 0,90 м / 3 = 0,60 м.

Решение c

Y_р = [2A sin kx]. cos ωt

Нам нужно подставить значения:

k = 2π / λ = k = 2π / 0,60 м = 10 π / 3

ω = 2π x 200 Гц = 400 π Гц.

Амплитуда 2А уже дается выражением:

= 0,5 см. грех [(10π / 3) х]. cos (400πt)

Ссылки

Индуктивность: формула и единицы, самоиндуктивность

Виртуальная реальность применительно к амаксофобии

Источник