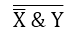Что такое структурная формула в информатике

Логика и компьютер

Вы будете перенаправлены на Автор24

Логика в информатике – это те отрасли знания и направления исследований, в которых логика применяется в информатике и искусственном интеллекте. В информатике логика оказалась гораздо более эффективной, чем это было в математике.

Основные направления прикладного использования логики в информатике

Стандартное математическое представление любого вычисления − это отображение переменных (их внутреннего состояния) вычислительного устройства на входе в новое состояние на выходе. В алгебре логики решается стандартная задача, а именно: определяется функциональная полнота логических связок, то есть проверяется, является ли фиксированный набор логических операций достаточным для того, чтобы представить новое результирующее значение путём комбинации любых других (базовых) функций. А это значит, что базовые логические устройства должны быть универсальными и позволять решать большое число задач.

Работу большинства вычислительных устройств, которые существуют в настоящее время, прекрасно описывает алгебра логики, разработанная Джорджем Булем. К таким устройствам относятся триггеры, сумматоры, группы переключателей, Кроме того булева алгебра и компьютеры связаны между собой при помощи используемой в ЭВМ двоичной системы счисления. Поэтому в устройствах компьютера можно хранить и преобразовывать и значения логических переменных, и числа.

Логические элементы — это электронные устройства, которые по определенному закону преобразуют проходящие через них двоичные электрические сигналы.

Готовые работы на аналогичную тему

Все электронные схемы компьютера могут быть реализованы с помощью трёх базовых логических элементов И, ИЛИ, НЕ.

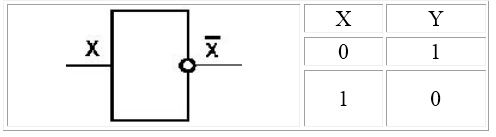
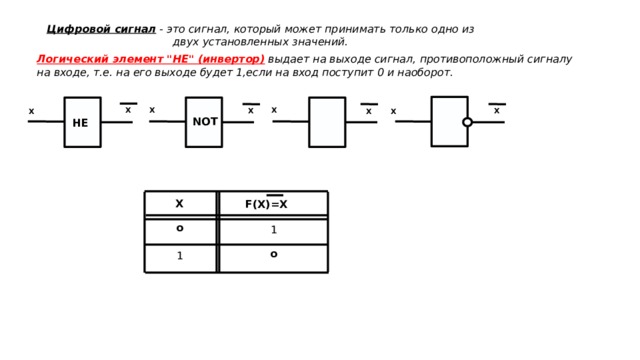
Логический элемент НЕ (инвертор). Простейший логический элемент, реализующий функцию отрицания (инверсию). Унарный элемент – элемент, у которого один вход и один выход.

На функциональных схемах обозначается

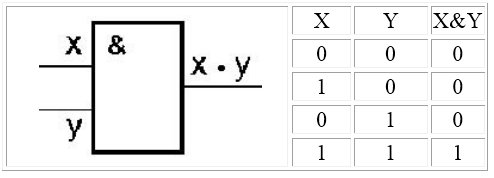
Логический элемент И (конъюнктор) реализует умножение двух или более логических значений, т.е. имеет два или более входов и один выход. На функциональных схемах обозначается:

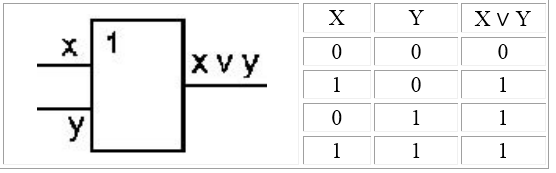
Логический элемент ИЛИ (дизъюнктор) реализует сложение двух или более логических значений, т.е. имеет два или более входов и один выход. На функциональных схемах обозначается:

Роль базовых логических элементов в создании схем играют ещё два логических элемента: И-НЕ и ИЛИ-НЕ.

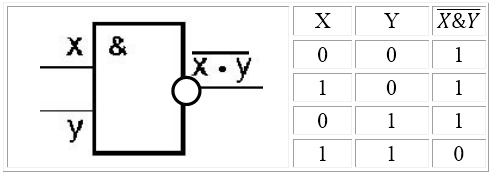
Логический элемент И-НЕ (отрицание конъюнкции) выполняет логическую функцию штрих Шеффера. Операция бинарная, поэтому имеет, как минимум, два входа. На функциональных схемах обозначается следующим образом:

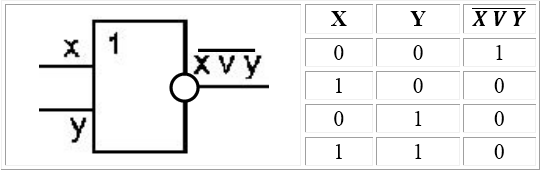
Логический элемент ИЛИ-НЕ (отрицание дизъюнкции) выполняет логическую функцию стрелка Пирса. Тоже бинарная операция, поэтому имеет, как минимум, два входа. На функциональных схемах обозначается так:

Функциональные схемы

Сигнал, который вырабатывает один логический элемент, можно подать на вход другого элемента. Это даст возможность образовать цепочку из отдельных логических элементов – функциональную схему.

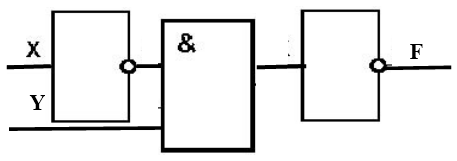
Функциональная (логическая) схема – это схема, которая выполняет определённую функцию и состоит из базовых логических элементов. Проанализировав фунциональную схему, можно понять, как работает логическое устройство, то есть ответить на вопрос, какую же функцию она выполняет. А чтобы описать функциональную схему, нужна структурная формула.

Как по заданной функциональной схеме записать структурную формулу?

Записали, что структурной формулой данной функциональной схемы является формула

Для функциональной схемы нужно составить таблицу значений сигналов на входах и выходах схемы, по которой можно понять, какую функцию выполняет данная схема, – таблицу истинности.

Обработка любой информации на компьютере − выполнение процессором различных арифметических и логических операций. Для этого в составе процессора есть арифметико-логическое устройство (АЛУ), которое состоит из ряда устройств, построенных на логических элементах, рассмотренных выше. Главными устройствами являются триггеры, полусумматоры, сумматоры, шифраторы, дешифраторы, счетчики, регистры.

Конструируется логическое устройство по следующему алгоритму:

Источник

III. Структурные формулы и функциональные схемы.

Соответствующие схемы называются функциональными. Анализируя функциональную схему, можно понять, как работает логическое устройство, т.е. дать ответ на вопрос: какую функцию она выполняет.
Не менее важной формой описания логических устройств является структурная формула. Покажем на примере как выписывают формулу по заданной функциональной схеме.

Ясно, что элемент «И» осуществляет логическое умножение значений 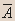и В.
Над результатом в элементе «НЕ» осуществляется операция отрицания, т.е. вычисляется значение выражения:

Формула и есть структурная формула логического устройства.
Задание 1. Для каждой из функциональных схем выписать соответствующую структурную формулу.

IV. Построение логического выражения по таблице истинности

Задача. По заданной таблице истинности построить логическое выражение и упростить его.
А).

V. Домашнее задание.

Задание 1. Для каждой из функциональных схем выписать соответствующую структурную формулу и заполнить таблицу работы.

Задание 2. Для каждой из cтруктурной формулы построить функциональную схему:

Задание 3. По заданной таблице истинности построить логическое выражение и упростить его.

УРОК 15-16.

ТЕМА УРОКА «ОСНОВНЫЕ УЗЛЫ ЭВМ»

Оборудование: ПК, компьютерная программа INFO (Элементы вычислительной техники в школьном курсе информатики (logika\5\. )).
Наглядность:

· презентация Узлы.ppt (logika\6\. );

· файлы: R1.htm, R2.htm, Sum1.htm, Sum2.htm, Triger1.htm, Triger2.htm, Triger3.htm (logika\2\11klass\file\urok15-16\. ).

· литература:

1) Семененко В.А. и др. Электронные вычислительные машины: Учебное пособие для ПТУ.- М.: Высш. Шк., 1991.

6) Лыскова В.Ю., Ракитина Е.А. Логика в информатике.-М.: Информатика и образование, 1999.

· опорный конспект;

· карточки (проверка домашнего задания, задание для индивидуальной работы);

· таблица «Успеваемость учащихся 11 кл. гимназии №5».

Цели урока:

1) Обеспечить усвоение учащимися алгоритма синтеза автомата;
2) ознакомить учащихся с основными узлами ЭВМ: сумматор, триггер, регистр;
3) отработать навыки построения функциональных схем, записи логических функций по таблице истинности, упрощения логических функций;
4) развитие навыков логического мышления;
5) формирование навыков работы с разными источниками информации.

ПЛАН УРОКА
1. Организационный момент.
2. Проверка домашнего задания.
3. Изучение нового материала.
4. Подведение итогов.
5. Домашнее задание.

II. Проверка домашнего задания (7 минут).
На прошлом уроке мы изучили тему «Двоичная арифметика». Дома вы должны были решить 8 примеров. Кто не справился с заданием? Проверим примеры. Проверку осуществим таким образом: я выдам вам всем решение, а вы проверите его. Итак, приступим к проверке.
Поднимите руки у кого нет ошибок (оценка 5), у кого 1 или 2 ошибки (оценка 4), 3-4 ошибки (оценка 3).

III. Изучение нового материала.
Замечательно! А теперь вспомните правила двоичной арифметики и ответьте на вопрос: операции сложения, вычитания, умножения, деления, в конечном счете, сводятся к каким операциям? (сложение, сдвиг, запоминание).
Сегодня на уроке вы узнаете, какие узлы ЭВМ их реализуют. Итак, тема нашего урока «Основные узлы ЭВМ».
Это последняя тема раздела «Введение в математическую логику и теорию автоматов». Вы познакомитесь с алгоритмом синтеза автоматов, с такими узлами ЭВМ как сумматор, триггер, регистр. На уроке мы отработаем навыки построения функциональных схем, записи логических функций по таблице истинности, упрощения логических функций, таким образом, подготовимся к контрольной работе.

Запишите в тетради вопросы, которые будут рассмотрены на уроке:

Источник

Всякое устройство ЭВМ, выполняющее некоторое действие над цифровыми сигналами, можно рассматривать как функциональный преобразователь, на входы которого с помощью цифровых сигналов подаются значения аргументов функции (исходные двоичные числа), а на выходах получают значения функций, реализующих указанное действие для этих аргументов (выходные двоичные числа).

Преобразователь, который, получая сигналы об истинности отдельных высказываний, обрабатывает их и в результате выдаёт значение логических операций (отрицания, суммы, произведения), называется логическим элементом.

1. Логический элемент «НЕ» (инвертор) выдаёт на выходе сигнал, противоположный сигналу на входе. То есть если на входе в инвертор поступает 1, то на выходе будет 0, и наоборот. Физически инвертор можно реализовать при помощи реле с нормально замкнутыми (подпружиненными) контактами. Когда на обмотку реле подаётся ток (входной сигнал равен 1), реле срабатывает и размыкает соединение. Когда тока в цепи нет, цепь становится замкнутой. Условное обозначение инвертора представлено на рисунке 6.

2. Логический элемент «И» (конъюнктор) выдаёт на выходе значение логического произведения входных сигналов. Физически конъюнктор можно реализовать последовательным соединением переключателей. Условное обозначение конъюнктора представлено на рисунке 7.

3. Логический элемент «ИЛИ» (дизъюнктор) выдаёт на выходе значение логического сложения входных сигналов. Физически дизъюнктор можно реализовать параллельным соединением переключателей. Условное обозначение конъюнктора представлено на рисунке 8.

4. Цепочку логических элементов, в которой выходы одних элементов являются входами других, называют логическим устройством.

Схема соединения логических элементов, реализующая логическую функцию, называется функциональной (логической) схемой.

Формой описания функции, реализуемой логическим устройством, является (структурная) формула.

Пример. Определим формулу по заданной функциональной схеме (см. рис. 9).

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

© 2014-2021 Все права на дизайн сайта принадлежат С.Є.А.

Источник

Логические основы ЭВМ. Функциональная схема. Структурная формула.

Содержимое разработки

Логические основы ЭВМ.

1673 г. Годфрид Вильгельм Лейбниц выдвинул идею применения в логике математической символики, предложил использовать двоичную систему счисления для целей вычислительной математики.

1848 г. Джордж Буль заложил основы алгебры логики (алгебры высказываний), поставив в соответствие истинному и ложному значениям числа 1 и 0.

1890 г. Герман Холлерит создал счетно-аналитическую машину, в которой впервые для расчетов были использованы электричество и перфокарты.

1938 г. Алан Мэтисон Тьюринг разработал теорию логических автоматов и доказал, что универсальная вычислительная машина теоретически возможна и ей по силам решение практически неограниченного числа различных задач.

1945 г. Джон фон Нейман сформулировал основные принципы архитектуры ЭВМ, в которых обосновал использование двоичной системы счисления для представления информации в вычислительных машинах.

Ученые сначала предположили, что возможно построение электронных схем на базе математической логики, затем построили такие схемы. Теперь всевозможные электронные схемы лежат в основе вычислительных машин. Аппарат математической логики находит применение в вычислительной математике и в технике при конструировании сложных автоматических устройств.

Цифровой сигнал — это сигнал, который может принимать только одно из двух установленных значений.

Логический элемент «НЕ» (инвертор) выдает на выходе сигнал, противоположный сигналу на входе, т.е. на его выходе будет 1,если на вход поступит 0 и наоборот.

Источник

Урок по информатике и ИКТ по теме «ЛОГИЧЕСКИЕ ОСНОВЫ ПОСТРОЕНИЯ ЭВМ» 10 класс (профильный уровень)

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Урок по информатике и ИКТ

10 класс (профильный уровень)

ЛОГИЧЕСКИЕ ОСНОВЫ ПОСТРОЕНИЯ ЭВМ

Цель урока: знакомство с логическими основами построения ЭВМ.

образовательная – сформировать представление о базовых логических элементах, объяснять работу основных логических элементов, научиться по структурной формуле строить функциональную схему и по функциональной схеме выписывать структурную формулу, составлять таблицу истинности для функциональной схеме.

развивающие – развитие логического и комбинационного мышления, памяти, внимательности, формирование элементов графической культуры;

воспитательные – воспитание познавательного интереса учащихся, умения слушать, аккуратности в работе, трудолюбия.

Тип урока: комбинированный урок.

Формы работы: фронтальная.

Учащиеся должны знать:

роль математической логики в создании ЭВМ;

основные базовые элементы логических схем;

правила составления логических схем.

Учащиеся должны уметь:

составлять электрические и логические схемы.

составлять логические выражения по функциональным схемам

Наглядность и оборудование:

презентация, подготовленная в MS PowerPoint (файл Логические основы ПК. ppt );

учебники Угриновича Н.Д. для 10-11 кл. (У. п.3.7.1), Шауцуковой Л.З. (Ш. п.5.3. – 5.6.).

1. Актуализация опорных знаний (6 минут).

2. Изучение новой темы (10 минут).

3. Решение задач (20 минут)

3. Подведение итогов урока. Домашнее задание (4 минуты).

Актуализация опорных знаний.

Как представляется информация в ЭВМ?

Почему двоичная система является необходимой для ЭВМ?

Назовите основные устройства компьютера.

Назначение основных устройств ЭВМ.

Что такое программный принцип управления ЭВМ?

Как работает компьютер? (Рассказ по схеме (файл Логические основы ПК. ppt слайд №4)).

Вопросы для рассмотрения темы.

Логические основы построения ЭВМ.

Структурные формулы и функциональные схемы.

ЛОГИЧЕСКИЕ ОСНОВЫ ПОСТРОЕНИЯ ЭВМ.

В основе обработки компьютером информации лежит алгебра логики, разработанная Дж. Булем. Было доказано, что все электронные схемы ЭВМ могут быть реализованы с помощью логических элементов И, ИЛИ, НЕ.

При подаче на вход схемы сигнала низкого уровня (0) транзистор будет заперт, т.е. ток через него проходить не будет, и на выходе будет сигнал высокого уровня (1). Если же на вход схемы подать сигнал высокого уровня (1), то транзистор “откроется”, начнет пропускать электрический ток. На выходе за счет падения напряжения установится напряжение низкого уровня. Т.о., схема преобразует сигналы одного уровня в другой, выполняя логическую функцию.

Здесь транзисторы включены параллельно друг другу. Если оба закрыты, то их общее сопротивление велико и на выходе будет сигнал низкого уровня (логический “0”). Достаточно подать сигнал высокого уровня (“1”) на один из транзисторов, как схема начнет пропускать ток, и на сопротивлении нагрузки установится также сигнал высокого уровня (логическая “1”).

Если на входы Вх1 и Вх2 поданы сигналы низкого уровня (логические “0”), то оба транзистора закрыты, ток через них не проходит, выходное напряжение на R_н близко к нулю.

Пусть на один из входов подано высокое напряжение (“1”). Тогда соответствующий транзистор откроется, однако другой останется закрытым, и ток через транзисторы и сопротивление проходить не будет. Следовательно, при подаче напряжения высокого уровня лишь на один из транзисторов схема не переключается и на выходе остается напряжение низкого уровня.

И лишь при одновременной подаче на входы сигналов высокого уровня (“1”) на выходе мы также получим сигнал высокого уровня.

СТРУКТУРНЫЕ ФОРМУЛЫ И ФУНКЦИОНАЛЬНЫЕ СХЕМЫ.

Схемы, изображенные на рис.1 и рис. 2 называются функциональными. Анализируя функциональную схему, можно понять, как работает логическое устройство, т.е. дать ответ на вопрос: какую функцию она выполняет.

Не менее важной формой описания логических устройств является структурная формула. Покажем на примере как выписывают формулу по заданной функциональной схеме.

Элемент «НЕ» осуществляет логическое отрицание, следовательно на выходе этого элемента . Элемент “И” осуществляет логическое умножение значений и В. Над результатом в элементе “НЕ” осуществляется операция отрицания, т.е. вычисляется значение выражения:

Формула и есть структурная формула логического устройства.

Выпишем формулу для схемы, изображенной на рисунке 1.

Задание 1. Для функциональной схемы выписать соответствующую структурную формулу и построить таблицу работы.

Ответы для задания №1.

Б)

Задание 2. Для каждой c труктурной формулы построить функциональную схему:

А) б)

2) Выучить конспект.

3) Выписать структурную формулу, описывающую состояние логической схемы. Составить таблицу истинности для функциональной схемы:

4) Упростить логическую функцию и построить функциональную схему.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

Курс повышения квалификации

Авторская разработка онлайн-курса

Ищем педагогов в команду «Инфоурок»

Урок по информатике и ИКТ по теме

«ЛОГИЧЕСКИЕ ОСНОВЫ ПОСТРОЕНИЯ ЭВМ»

10 класс (профильный уровень)

Цель урока: знакомство с логическими основами построения ЭВМ.

Математическая логика с развитием ВТ оказалась в тесной взаимосвязи с вопросами конструирования и программирования вычислительной техники. Алгебра логики нашла широкое применение первоначально при разработке релейно-контактных схем. Первым фундаментальным исследованием, обратившим внимание инженеров, занимавшихся проектированием ЭВМ, невозможность анализа электрических цепей с помощью булевой алгебры была опубликована в декабре 1938 года статья американца Клода Шеннона «Символический анализ релейно-контактных схем». После этой статьи проектирование ЭВМ не обходилось без применения булевой алгебры.

Номер материала: 182232

Не нашли то, что искали?

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Все школы РФ с 2023 года подключат к государственной информационной системе «Моя школа»

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Во всех педвузах страны появятся технопарки

Время чтения: 1 минута

Зарплаты педагогов Ростовской области вырастут в среднем на 10-15%

Время чтения: 2 минуты

Правительство направит регионам почти 92 миллиарда рублей на ремонт и оснащение школ

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник