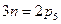Что такое структурная группа

Что такое структурная группа

Механизмом называется система связаных твердых тел, предназначеных для передачи и преобразования движения одного или нескольких тел в требуемое движение других тел.

Элементы механической системы :

Классификация кинематических пар.

Основные понятия структурного синтеза и анализа.

Основные структурные формулы.

Для расчета избыточных связей :

Структурная классификация механизмов по Ассуру Л.В.

По этой классификации механизмы не имеющие избыточных связей и местных подвижностей состоят из первичных механизмов и структурных групп Ассура (см. рис.1.2).

Под первичным механизмом понимают механизм, состоящий из двух звеньев (одно из которых неподвижное) образующих кинематическую пару с одной W_пм = 1 или несколькими W_пм > 1 подвижностями.
Структурной группой Ассура (или группой нулевой подвижности) называется кинематическая цепь, образованная только подвижными звеньями механизма, подвижность которой (на плоскости и в пространстве) равна нулю (W_гр = 0).
Конечные звенья групп Ассура, входящие в две кинематические пары, из которых одна имеет свободный элемент звена, называются поводками. Группы могут быть различной степени сложности. Структурные группы Ассура делятся на классы в зависимости от числа звеньев, образующих группу, числа поводков в группе, числа замкнутых контуров внутри группы. В пределах класса (по Ассуру) группы подразделяются по числу поводков на порядки (порядок группы равен числу ее поводков). Механизмы классифицируются по степени сложности групп входящих в их состав. Класс и порядок механизма определяются классом и порядком наиболее сложной из входящих в него групп. Особенность структурных групп Ассура-их статическая определимость. Если группу Ассура свободными элементами звеньев присоеденить к стойке, то образуется статически определимая ферма. Используя группы Ассура удобно проводить структурный, кинематический и силовой анализ механизмов.

Проведем структурный анализ плоского механизма, схема которого приведена на рис.1.1 и представим его в виде совокупности первичного механизма и структурных групп Ассура. Результаты структурного анализа изображены на рис.1.3. Для рассматриваемого механизма структурный анализ можно проводить только для плоской модели, так как она не содержит избыточных связей. Механизм состоит из двух рычажных двухповодковых групп (1-й класс 2-ой порядок). Если рассмотреть полученные структурные группы как пространственные, то они не будут группами нулевой подвижности ибо обладают избыточными связями. Чтобы преобразить их в группы с нулевой подвижностью снизим классы кинематических пар, не допуская при этом возникновения местных подвижностей. По группам звеньев классы пар изменяются так :

После таких изменений классов КП подвижность механизма :

В данном случае для устранения избыточных связей мы воспользовались способом снижения классов КП. В заключение необходимо отметить, что устранять избыточные связи нужно не всегда. Многоподвижные КП сложнее и дороже в изготовлении, механизмы с такими парами часто обладают меньшей жесткостью и точностью, чем механизмы с одноподвижными КП.

Источник

Что такое структурная группа

Лабораторная работа № 1.

Структурный и кинематический анализ рычажных механизмов.

Цель и задачи работы : изучение основных положений и принципов структурного анализа плоских рычажных механизмов; знакомство с правилами составления структурных схем механизмов, условными обозначениями их элементов по ГОСТ-2.770-68, классификацией механизмов по Ассуру; проведение структурного анализа для заданного рычажного механизма, проверка правильности выполненного анализа на ЭВМ.

Кинематические пары классифицируются по следующим признакам:

Например, вращательная и поступательная КП являются низшими одноподвижными парами 5-го класса.

При проведении теоретических и экспериментальных исследований пользуются различными расчетными схемами и моделями механизмов и машин. Они обычно отражают только те свойства механизмов и машин, которые существенно влияют на исследуемые характеристики. Так, при анализе структуры механизма используют его структурную схему; при анализе кинематики — кинематическую; динамики — динамическую. Структурная схема механизма должна содержать информацию о числе его звеньев и их взаимном расположении, виде расположении и классе (или числе подвижностей) кинематических пар. Структурную схему механизма вычерчивают по определенным правилам с использованием условных обозначений, регламентированных ГОСТ 2.770-68. Некоторые обозначения, необходимые для выполнения данной работы, приведены в табл.1.1.

Графическое изображение элементов структурных схем

Наименование		Графическое изображение
	Ползун Втулка Поршень Камень
	Кривошип Шатун Коромысло Кулиса
	Вращательные
	Поступательные

W пр = (1.1)

где n=(k-1) — число подвижных звеньев механизма; k — общее число звеньев (вместе со стойкой); i — число подвижностей в КП; p i — число КП с i подвижностями в механизме.

Если движение звеньев механизма происходит в параллельных плоскостях, то его можно рассматривать как плоский. В этом случае подвижность определяют по формуле Чебышева:

W пл =. (1.2)

При расчете подвижности механизма в пространстве необходимо учитывать, что при переходе от плоского представления механизма к пространственному число подвижностей каждого звена увеличивается с трех до шести. При этом подвижность некоторых пар может увеличиться. Так в плоском механизме сферические и цилиндрические пары относятся к одноподвижным низшим. В пространственном они становятся: сферическая – трехподвижной, цилиндрическая – двухподвижной.

Большинство механизмов, применяющихся в современных машинах, имеет одну подвижность. При этом достаточно задать движение одному звену для осуществления вполне определенного движения всех остальных. Механизм с W>1 используют реже. Для многих механизмов при расчете по формуле (1.1) получают отрицательное значение или нуль. Однако анализ движения рассматриваемого механизма показывает, что число его подвижностей равно единице. Такое расхождение возникает, если в схеме механизма имеются повторяющиеся или избыточные связи.

Избыточными называют такие связи в механизме, которые дублируют уже имеющиеся и не изменяют его реальной подвижности. Их вводят в структуру механизма с целью повышения его жесткости и точности. Число избыточных связей q в механизме можно определить после задания его подвижности W 0 (часто W 0 =1 ):

Величина q определяет степень статической неопределимости механизма при силовом расчете.

1.2. Классификация рычажных механизмов по Ассуру.

Для плоских механизмов с низшими КП Ассуром Л.В. была разработана система классификации, в которой механизмы состоят из первичных механизмов и структурных групп Ассура (групп нулевой подвижности). Первичным механизмов (рис.1) называют механизм, состоящий из двух звеньев: 1, 0 (одно из них неподвижное — стойка), которые образуют одноподвижную пару (вращательную или поступательную).

Сложная группа Ассура не может быть образована комбинацией простых групп более низкого класса или порядка. Некоторые примеры групп Ассура 1-го класса 2-го и 3-го порядков приведены в табл.1.2.

Структурные группы Ассура.

Группы Ассура 1-го класса 2-го порядка (2-го класса 2-го порядка)*

Группы Ассура 1-го класса 3-го порядка (3-го класса 3-го порядка)*

* в скобках указан класс и порядок группы по классификации И.И.Артоболевского

На рис. 1.3 изображена структурная схема плоского рычажного восьмизвенного механизма, где арабскими цифрами (от 0 до 7) обозначают звенья, причем символом «0» — стойку; прописными латинскими бувами — кинематические пары.

Источник

Для выполнения структурного синтеза (проектирования схемы) многозвенных плоских механизмов с числом звеньев более четырех непосредственный перебор всех возможных вариантов по формуле Чебышева оказывается затруднительным. Наиболее удобно проектировать схемы механизмов путем наслоения (присоединения) кинематических цепей, называемых структурными группами, или группами Ассура. Понятие о структурных группах введено в 1916 г. Л.В. Ассуром.

NB 3.3. Группой Ассура называется такая плоская кинематическая цепь, которая, будучи присоединенной к другой кинематической цепи, не меняет числа степеней свободы последней.

Иначе говоря, число степеней свободы группы Ассура W = 0. Группа Ассура содержит только низшие кинематические пары. При таких условиях структурная формула группы Ассура имеет вид:

Это условие в целых числах удовлетворяется только при четных числах звеньев n и числах низших кинематических пар p₁, кратных трем, и может быть представлено соотношениями, приведенными в табл. 3.3:

Число подвижных звеньев

Число кинематических пар

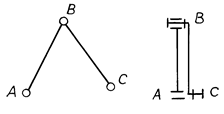
Из табл. 3.3 видно, что простейшая группа Ассура состоит из двух звеньев и трех низших кинематических пар. Базовая группа Ассура содержит два звена и три вращательные пары (рис. 3.5). В точке B находится действительная кинематическая пара (цилиндрический шарнир). В точках A и C — потенциальные пары, которыми группа Ассура, входящая в состав механизма, присоединяется к соседним звеньям.

1. Группа Ассура — плоская кинематическая цепь с числом степеней свободы, равным нулю.

2. Группа Ассура содержит только низшие пары.

3. Простейшая группа Ассура состоит из двух звеньев и трех пар.

3.5. Классификация групп Ассура

Группы Ассура характеризуются классом и порядком.

1. Класс группы Ассура определяется числом кинематических пар, входящих в наиболее сложный контур.

2. Порядок группы Ассура определяется числом внешних (потенциальных) кинематических пар.

Таким образом, в соответствии с данными определениями простейшая группа Ассура (рис. 3.5) является группой II класса и 2-го порядка: каждый из контуров (AB и BC) входит в две кинематические пары, потенциальными являются две пары — A и C. Простейшая группа Ассура называется двухповодковой, или диадой. В формуле строения порядок группы Ассура указывают в индексе класса, например III₃. Так как двухповодковые группы всегда второго порядка, то в индексе их класса ставится вид. Базовой диаде (рис. 3.5) присвоен вид 1 и обозначение II₁. В табл. 3.4 приведены некоторые виды контуров и групп Ассура.

Источник

В современном машиностроении все многообразие механизмов разбито на различные классы и группы в зависимости от общих классификационных признаков.

Структурный анализ механизма всегда предшествует его кинематическому и силовому расчетам.

Механизмы одного и того же класса имеют общие методы расчетов.

Деление механизмов на классы производится по структурным особенностям групп, составляющих данные механизм.

Структурные группы. Класс, порядок, вид групп Ассура. Согласно Л.В.Ассуру любой механизм образуется последовательным присоединением к входному звену (со стойкой) кинематических цепей, степень подвижности которых равна нулю. Такие цепи называются структурными группами Ассура. Если степень подвижности W=0, то число звеньев и пар плоского механизма, входящих в группу, связаны соотношением

Это уравнение имеет множество решений, состоящих из четного числа звеньев и кинематических пар 5-го класса, количество которых кратно 3.

Группами Ассура будут являться только неделимые цепи, т.е. такие, которые без разрушения нельзя разделить на самос­тоятельные структурные группы.

Класс, порядок, вид структурных групп. Группы Ассура разделяются на классы, каждая структурная группа имеет порядок, а в одном из классов, втором, различают еще и виды групп.

Класс группы Ассура определяется наивысшим классом контура, входящего в ее состав (табл. 1)

Таблица1

Кинематическая цепь, состоящая из двух звеньев и трех кинематических пар (n=2; ), всегда является группой Ассура второго класса.

Порядок структурной группы определяется числом внешних, свободных кинематических пар, которыми она присоединяется к другим звеньям механизма. В табл. 1 внешние пары затушеваны, они и определяют порядок структурной группы. Кинематические пары, входящие в замкнутый контур, называются внутренними. У групп Ассура второго класса всегда 2-й порядок.

Группы Ассура 2-го класса разделяются на пять видов, зави­сящих от взаимного расположения в группе вращательных и поступательных кинематических пар.

Виды групп Ассура 2-го класса представлены на рис. 1.

Рис. 1. Виды групп Ассура 2-го класса

Класс группы Ассура выше второго определяется числом внутренних кинематических пар, образующих замкнутый контур (табл. 1, контуры 3 и 4). Ведущее звено вместе со стойкой и кинематической парой, соединяющей их, называется механизмом 1-го класса и ука­зывается стрелкой, направленной по движению ведущего звена.

Рис.2. Вращающееся ведущее (а) и поступательно движущееся (б) звенья

На рис. 2а представлено вращающееся ведущее звено, а на рис.2б

поступательно движущееся. Конструктивные особенности звеньев, не оказывающие влияния на движение механизма, на схемах не учитываются.

Класс механизма определяется наивысшим классом структурной группы, входящей в этот механизм. При определении класса механизма необходимо указать, какие звенья являются ведущими, т. к. в зависимости от выбора ведущих звеньев класс механизма может измениться.

В структурные группы входят только цепи с низшими кинематическими парами. Если в механизме имеются цепи с высшими кинематическими парами, каждая высшая пара должна быть заменена, и только после этого заменяющий механизм разбивается на структурные группы Ассура.

2. Замена высшей пары в плоском механизме

Каждая высшая кинематическая пара эквивалентна одному звену, оканчивающемуся двумя низшими парами. Вид низших пар зависит от соприкасающихся поверхностей звеньев.

Рис.3. Замена высших пар низшими

3.Структурный анализ механизма

Структурным анализом механизма называют определение количества ведущих звеньев, групп Ассура, последовательность их присоединения к кинематической цепи и класс механизма.

Структурный анализ возможен, если соблюдаются следующие условия:

I)число ведущих звеньев равно числу степеней свободы механизма;

2) ведущее звено входит в кинематическую пару со стойкой;

3)все кинематические пары относятся к 5-му классу.

Структура любого плоского механизма наглядно представ­ляется с помощью формулы его строения. Формула строения механизма состоит из условного обозначения класса, порядка и вида каждой структурной группы, и схематично показывает порядок присоединения структурных групп к ведущим звеньям.

Например, если формула строения механизма

В группе Ассура 3-го класса, 3-го порядка в скобках указаны номера звеньев, ее образующие. Одно из них поставлено в числителе, и оно носит название базисного, потому что к нему присоединяются более чем два других звена (их номера перечислены в знаменателе: 5, 6, 7).

4. Порядок проведения структурного анализа

1. Подсчитывается степень подвижности механизма по формуле Чебышева, для чего нумеруются подвижные звенья и определяется количество кинематических пар. При наличии высших кинематических пар их надо заменить цепями с низшими кинематическими парами.

Если в механизме есть лишние степени подвижности, их не учитывают. Могут оказаться в механизме и пассивные связи, которые не оказывают влияния на работу механизма. Применяются они в механизмах для увеличения жесткости, для более пра­вильного распределения нагрузок. Лишние степени свободы служат для увеличения к.п.д. механизма и уменьшения износа.

Производится отделение групп Ассура, начиная с наиболее удаленной от ведущего звена. Если возможно, отделяется группа наиболее низкого класса. Если такую группу выделить невозможно, отделяется группа более высокого класса. Разложение механизма на структурные группы ведется до тех пор, пока не останутся ведущее звено и стойка. При этом необходимо проверять замкнутость оставшейся кинематической цепи. Каждое звено и любая кинематическая пара должны входить только в одну из структурных групп.

Записывается формула строения механизма, начиная с ведущего звена (механизма 1-го класса) и далее в порядке присоединения групп Ассура.

Указывается класс механизма.

5.Примеры структурного анализа

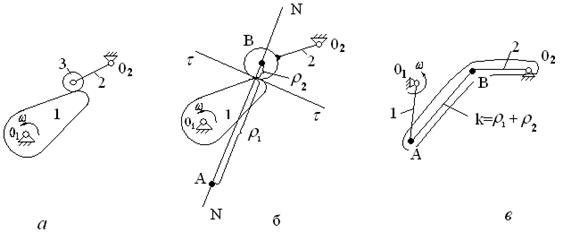
Пример 1. Кулачково-коромысловый механизм

Степень подвижности механизма

Ведущим звеном выбран кулачок 1.

Высшая пара должна быть заменена добавочным условным звеном k (длина которого равна сумме радиусов кривизны и соприкасающихся поверхностей 1 и 2) и двумя низшими парами А и В, расположенными в центрах кривизны (рис. 4в).

Рис.4 Пример структурного анализа механизма с лишней степенью подвижности и высшей кинематической парой

Мгновенно заменяющий механизм представлен на рис.4в.

Кинематическая цепь этого механизма состоит из структурной группы 2-го класса,2-го порядка и 1-го вида и ведущего звена . Формула его строения:

.

Заменяющий механизм относится к механизму 2-го класса.

Исходный кулачковый механизм также относится к механизму 2-го класса.

Пример 2. Механизм с изменяемым классом

Рис.5.Пример структурного анализа механизма с изменяемым классом

Степень подвижности исходного механизма при n=5 и (рис.5а) W=3*5-2*7=1 указывает на наличие в нем одного ведущего звена.

Допустим, что входным звеном выбрано звено 1 (рис.5б). Делается попытка отделить от механизма группу Ассура 2-го класса ((n =2, ); звенья 3 и 4). Тогда оставшаяся цепь звеньев 1, 2, 5 будет незамкнутой, что приводит к неопределенности движения звеньев 2 и 5. Тот же результат получается при отделении от механизма звеньев 4, 5.

1(0,4)- (2,3,4,5),

т.е. механизм 4-го класса.

Если в данном механизме выбрать за входное звено 4, то класс его изменяется (рис. 5г). Цепь его ведомых звеньев 1, 2, 3, 5 представляет собой трехповодковую группу Ассура 3-го класса 3-го порядка. Формула строения механизма в этом случае:

1(0,4)- (2,1,3,5),

т.е механизм 3-го класса.

Таким образом, замена ведущего (начального) звена привела к понижению класса механизма.

Источник

Что такое структурная группа

Лабораторная работа № 1.

Структурный и кинематический анализ рычажных механизмов.

Цель и задачи работы : изучение основных положений и принципов структурного анализа плоских рычажных механизмов; знакомство с правилами составления структурных схем механизмов, условными обозначениями их элементов по ГОСТ-2.770-68, классификацией механизмов по Ассуру; проведение структурного анализа для заданного рычажного механизма, проверка правильности выполненного анализа на ЭВМ.

Кинематические пары классифицируются по следующим признакам:

Например, вращательная и поступательная КП являются низшими одноподвижными парами 5-го класса.

При проведении теоретических и экспериментальных исследований пользуются различными расчетными схемами и моделями механизмов и машин. Они обычно отражают только те свойства механизмов и машин, которые существенно влияют на исследуемые характеристики. Так, при анализе структуры механизма используют его структурную схему; при анализе кинематики — кинематическую; динамики — динамическую. Структурная схема механизма должна содержать информацию о числе его звеньев и их взаимном расположении, виде расположении и классе (или числе подвижностей) кинематических пар. Структурную схему механизма вычерчивают по определенным правилам с использованием условных обозначений, регламентированных ГОСТ 2.770-68. Некоторые обозначения, необходимые для выполнения данной работы, приведены в табл.1.1.

Графическое изображение элементов структурных схем

Наименование		Графическое изображение
	Ползун Втулка Поршень Камень
	Кривошип Шатун Коромысло Кулиса
	Вращательные
	Поступательные

W пр = (1.1)

где n=(k-1) — число подвижных звеньев механизма; k — общее число звеньев (вместе со стойкой); i — число подвижностей в КП; p i — число КП с i подвижностями в механизме.

Если движение звеньев механизма происходит в параллельных плоскостях, то его можно рассматривать как плоский. В этом случае подвижность определяют по формуле Чебышева:

W пл =. (1.2)

При расчете подвижности механизма в пространстве необходимо учитывать, что при переходе от плоского представления механизма к пространственному число подвижностей каждого звена увеличивается с трех до шести. При этом подвижность некоторых пар может увеличиться. Так в плоском механизме сферические и цилиндрические пары относятся к одноподвижным низшим. В пространственном они становятся: сферическая – трехподвижной, цилиндрическая – двухподвижной.

Большинство механизмов, применяющихся в современных машинах, имеет одну подвижность. При этом достаточно задать движение одному звену для осуществления вполне определенного движения всех остальных. Механизм с W>1 используют реже. Для многих механизмов при расчете по формуле (1.1) получают отрицательное значение или нуль. Однако анализ движения рассматриваемого механизма показывает, что число его подвижностей равно единице. Такое расхождение возникает, если в схеме механизма имеются повторяющиеся или избыточные связи.

Избыточными называют такие связи в механизме, которые дублируют уже имеющиеся и не изменяют его реальной подвижности. Их вводят в структуру механизма с целью повышения его жесткости и точности. Число избыточных связей q в механизме можно определить после задания его подвижности W 0 (часто W 0 =1 ):

Величина q определяет степень статической неопределимости механизма при силовом расчете.

1.2. Классификация рычажных механизмов по Ассуру.

Для плоских механизмов с низшими КП Ассуром Л.В. была разработана система классификации, в которой механизмы состоят из первичных механизмов и структурных групп Ассура (групп нулевой подвижности). Первичным механизмов (рис.1) называют механизм, состоящий из двух звеньев: 1, 0 (одно из них неподвижное — стойка), которые образуют одноподвижную пару (вращательную или поступательную).

Сложная группа Ассура не может быть образована комбинацией простых групп более низкого класса или порядка. Некоторые примеры групп Ассура 1-го класса 2-го и 3-го порядков приведены в табл.1.2.

Структурные группы Ассура.

Группы Ассура 1-го класса 2-го порядка (2-го класса 2-го порядка)*

Группы Ассура 1-го класса 3-го порядка (3-го класса 3-го порядка)*

* в скобках указан класс и порядок группы по классификации И.И.Артоболевского

На рис. 1.3 изображена структурная схема плоского рычажного восьмизвенного механизма, где арабскими цифрами (от 0 до 7) обозначают звенья, причем символом «0» — стойку; прописными латинскими бувами — кинематические пары.

Источник