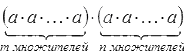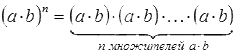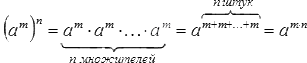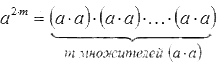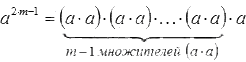Что такое свойство степени

Степени и их свойства

Данная тема очень легкая, если выучить все свойства степеней. Они, кстати, достаточно просты для запоминания.

Перед тем, как перейти в свойствам степеней, разберемся, что такое степень.

Показатель степени показывает (масло масляное) сколько раз мы умножаем основание на себя. Это очень хорошо проглядывается на следующих примерах:

Вроде бы ничего сложного нет, правда?

Что ж, время перейти к свойствам.

Свойства степеней.

1. Любое число в первой степени равно самому себе: a 1 = a.

Сразу рассмотрим примеры.

2. Любое число в нулевой степени равно 1: а 0 = 1.

3. Единица в любой степени равна 1: 1 n = 1.

Это свойство легко доказать на числовом примере.

Конечно, так никто не расписывает, а сразу пользуется готовой формулой. Вот еще несколько примеров:

3 4 · 3 9 · 3 15 = 3 4 + 9 + 15 = 3 2 8 ;

Еще парочка примеров:

(2 2 ) 3 = 2 2 · 3 = 2 6 ;

8. Чтобы возвести дробь в степень надо и числитель, и знаменатель возвести в эту степень:.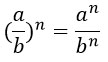

9. Степень с дробным показателем можно представить в виде корня некоторой степени по формуле 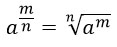(а > 0, n ≥ 2).

10. Чтобы возвести число, отличное от нуля, в степень с отрицательным показателем надо взять число, обратное данному, и возвести его в ту же степень, только без минуса: 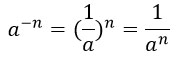(a ≠ 0).

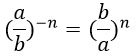
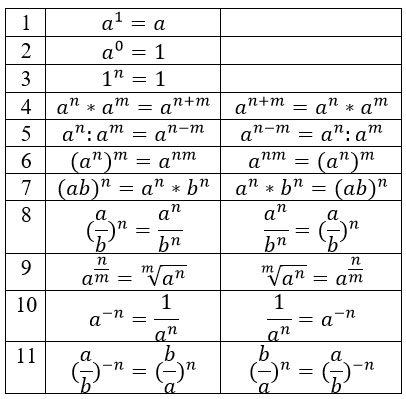
Это же правило работает и для дробей: (a ≠ 0, b ≠ 0).

Все эти свойства срабатывают как в одну сторону, так и в другую. Соберем их в аккуратную табличку.

Нам нужно сократить такую дробь:

Преобразуем знаменатель дроби, дважды использовав формулу по номером 5 из второго столбика таблицы.

Получившиеся частные в знаменателе запишем в виде дробей.

Получилась трехярусная дробь (можно произведение дробей в знаменателе переписать под одну черту). Нижний ярус этой дроби перейдет в верхний. Это не магия вне Хогвартса, но описывать эти преобразования текстом очень грустно. Если коротенько, то при делении на дробь мы ее переворачиваем и получается, что знаменатель заползает наверх 🙂

Переходим к финалу. Преобразуем знаменатель по свойству 7 из второго столбика таблицы (снова) и, наконец-таки, сокращаем дробь!

Источник

Свойства степеней. Действия со степенями

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Что такое степень числа

В учебниках по математике можно встретить такое определение:

«Степенью n числа а является произведение множителей величиной а n раз подряд»

a — основание степени;

n — показатель степени.

Читается такое выражение, как a в степени n

Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) само на себя.

А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:

2 — основание степени;

3 — показатель степени.

Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.

Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.

Задачка про миллион: представьте, что у вас есть миллион рублей. В начале каждого года вы зарабатываете на нем еще два. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.

Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:

Математики заскучали и решили все упростить:

Ответ: через четыре года у вас будет 81 миллион.

Таблица степеней

Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).

Источник

Степень и ее свойства. Определение степени

Разделы: Математика

Ознакомить учащихся со свойствами степеней с натуральными показателями и научить выполнять действия со степенями.

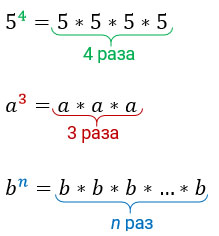
Степенью числа a с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен а. Степенью числа а с показателем 1 называется само число а.

По определению степени:

а n =

Нахождение значения степени называют возведением в степень.

1. Примеры возведения в степень:

2. Представьте в виде квадрата числа: 25 ; 0,09 ;

25 = 5 2 ; 0,09 = ( 0,3 ) 2 ; .

3. Представьте в виде куба числа:

4. Найти значения выражений:

а) 3• 10 3 = 3• 10• 10• 10 = 3• 1000 = 3000

1. Запишите произведение в виде степени:

б)

2. Представьте в виде квадрата числа:

16 ; 0,25 ; .

3. Представьте в виде куба числа:

125 ; 0,027 ; .

4. Найти значения выражений :

Для любого числа а и произвольных чисел m и n выполняется:

Правило: При умножении степеней с одинаковыми основаниями основания оставляют прежним, а показатели степеней складывают.

a m a n a k = a m + n a k = a ( m + n ) + k = a m + n + k

1. Представить в виде степени:

б) y• y 6 = y 1 • y 6 = y 1 + 6 = y 7

в) b 2 • b 5 • b 4 = b 2 + 5 + 4 = b 11

г) 3 4 • 9 = 3 4 • 3 2 = 3 6

д) 0,01• 0,1 3 = 0,1 2 • 0,1 3 = 0,1 5

2. Представить в виде степени и найти значение по таблице:

б) 3 2 • 3 5 = 3 7 = 2187

1. Представить в виде степени:

д) 2 3 •2 4 к) 0,3 3 •0,09

2. Представить в виде степени и найти значение по таблице:

б) 3 4 •3 2 г) 27• 243

Для любого числа а0 и произвольных натуральных чисел m и n, таких, что m>n выполняется:

по определению частного:

Правило: При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

Определение: Степень числа а, не равного нулю, с нулевым показателем равна единице:

1. Представьте в виде степени частное:

г) с 5 :с 0 = с 5 :1 = с 5

2. Найдите значения выражений:

б) 10 20 :10 17 = 10 3 = 1000

в)

г)

д)

1. Представьте в виде степени частное:

2. Найдите значения выражений:

в)

г)

д)

Возведение в степень произведения.

Для любых а и b и произвольного натурального числа n:

По определению степени

( ab ) n =

Сгруппировав отдельно множители а и множители b, получим:

=

Доказанное свойство степени произведения распространяется на степень произведения трех и более множителей.

( a• b• c ) n = a n •b n •c n ;

Правило: При возведении в степень произведения возводят в эту степень каждый множитель и результат перемножают.

1. Возвести в степень:

б) (2• х• у ) 3 =2 3 •х 3 •у 3 = 8• х 3 •у 3

в) ( 3• а ) 4 = 3 4 •а 4 = 81• а 4

д) (-0,2• х• у ) 2 = (-0,2) 2 •х 2 •у 2 = 0,04• х 2 •у 2

е) (-3• a• b• c ) 4 = (-3) 4 •a 4 •b 4 •c 4 = 81• a 4 •b 4 •c 4

2. Найти значение выражения:

а) (2• 10) 4 = 2 4 •10 4 = 16• 1000 = 16000

б) (3• 5• 20) 2 = 3 2 •100 2 = 9• 10000= 90000

в) 2 4 •5 4 = (2• 5) 4 = 10 4 = 10000

г) 0,25 11 •4 11 = (0,25• 4) 11 = 1 11 = 1

д)

1. Возвести в степень:

е)

2. Найти значение выражения:

г)

д)

Возведение в степень степени.

Для любого числа а и произвольных натуральных чисел m и n:

По определению степени

( а m ) n =

Правило: При возведении степени в степень основание оставляют тем же, а показатели перемножают.

1. Возвести в степень:

( а 3 ) 2 = а 6 ( х 5 ) 4 = х 20

( у 5 ) 2 = у 10 ( b 3 ) 3 = b 9

2. Упростите выражения:

а) а 3 •( а 2 ) 5 = а 3 •а 10 = а 13

б) ( b 3 ) 2 •b 7 = b 6 •b 7 = b 13

в) ( х 3 ) 2 •( х 2 ) 4 = х 6 •х 8 = х 14

г) ( у• у 7 ) 3 = ( у 8 ) 3 = у 24

3. Найдите значение выражений:

а)

б)

1. Возвести в степень:

в) ( у 3 ) 2 г) ( b 4 ) 4

2. Упростите выражения:

3. Найдите значение выражений:

а)

б)

Приложение

1ю Запишите произведение в виде степени:

б)

2. Представьте в виде квадрата числа:

25 ; 0,16 ; .

3. Представьте в виде куба числа:

64 ; 0,125 ; .

4. Найти значения выражений:

1. Запишите произведение в виде степени:

б)

в) с• с• с• с• с• с• с• с• с

2. Представьте в виде квадрата числа: 100 ; 0,49 ; .

3. Представьте в виде куба числа:

1000 ; 0,008 ; .

4. Найти значения выражений :

1. Запишите произведение в виде степени:

б)

д) ( bс ) • ( bс ) • ( bс ) • ( bc )

2. Представьте в виде квадрата числа:

81 ; 0,64 ;.

3. Представьте в виде куба числа:

216 ; 0,064 ; .

4. Найти значения выражений :

1. Представить в виде степени:

д) 2 2 •2 5 к) 0,2 3• 0,04

2. Представить в виде степени и найти значение по таблице:

1. Представить в виде степени:

д) 2 3 •2 6 к) 0,3 4 •0,27

2. Представить в виде степени и найти значение по таблице:

1. Представить в виде степени:

б) х 7 •х 8 ж) 3 4 •27

д) 2 4 •2 5 к) 0,2 2 •0,008

2. Представить в виде степени и найти значение по таблице:

1. Представьте в виде степени частное:

2. Найдите значения выражений:

в)

г)

д)

1. Представьте в виде степени частное:

2. Найдите значения выражений:

в)

г)

д)

1. Представьте в виде степени частное:

2. Найдите значения выражений:

в)

г)

д)

Возведение в степень произведения.

1. Возвести в степень:

2. Найти значение выражения:

д)

1. Возвести в степень:

е)

2. Найти значение выражения:

г)

1. Возвести в степень:

2. Найти значение выражения:

д)

Возведение в степень степени.

1. Возвести в степень:

2. Упростите выражения:

3. Найдите значение выражений:

а)

б)

1. Возвести в степень:

2. Упростите выражения:

3. Найдите значение выражений:

а)

б)

1. Возвести в степень:

2. Упростите выражения:

3. Найдите значение выражений:

а)

б)

Источник

Свойства степеней: формулировки, доказательства, примеры

Ранее мы уже говорили о том, что такое степень числа. Она имеет определенные свойства, полезные в решении задач: именно их и все возможные показатели степени мы разберем в этой статье. Также мы наглядно покажем на примерах, как их можно доказать и правильно применить на практике.

Свойства степени с натуральным показателем

1. Главное свойство степени: a m · a n = a m + n

2. Свойство частного для степеней, имеющих одинаковые основания: a m : a n = a m − n

3. Свойство степени произведения: ( a · b ) n = a n · b n

Равенство можно расширить до: ( a 1 · a 2 · … · a k ) n = a 1 n · a 2 n · … · a k n

4. Свойство частного в натуральной степени: ( a : b ) n = a n : b n

Можно обобщить до: ( ( ( a n 1 ) n 2 ) … ) n k = a n 1 · n 2 · … · n k

6. Сравниваем степень с нулем:

7. Равенство a n b n будет справедливо для любого натурального n при условии, что a и b больше нуля и не равны друг другу.

8. Неравенство a m > a n будет верным при условии, что m и n – натуральные числа, m больше n и а больше нуля и не меньше единицы.

Далее мы разберем каждое свойство подробно и попробуем привести доказательства.

Основное определение степеней с натуральными показателями позволит нам преобразовать равенство в произведение множителей. Мы получим запись такого вида:

Разберем конкретный пример, подтверждающий это.

Выполним необходимые математические действия: 2 2 · 2 3 = ( 2 · 2 ) · ( 2 · 2 · 2 ) = 4 · 8 = 32 и 2 5 = 2 · 2 · 2 · 2 · 2 = 32

Теперь мы можем перейти к доказательству. Из ранее изученного вспомним основные свойства дробей и сформулируем равенство так:

a m − n · a n = a ( m − n ) + n = a m

Из него можно вывести: a m − n · a n = a m

Подставим конкретные числа для наглядности в показатели, а основание степени обозначим π : π 5 : π 2 = π 5 − 3 = π 3

Согласно базовому определению степени с натуральным показателем мы можем переформулировать равенство так:

Если множителей у нас три и больше, то это свойство также распространяется и на этот случай. Введем для числа множителей обозначение k и запишем:

( a 1 · a 2 · … · a k ) n = a 1 n · a 2 n · … · a k n

Начнем сразу с примера: ( 5 2 ) 3 = 5 2 · 3 = 5 6

А теперь сформулируем цепочку равенств, которая докажет нам верность равенства:

a p q y s = a p · q · y · s

6. Еще одно свойство степеней с натуральным показателем, которое нам нужно доказать, – свойство сравнения.

Если умножить одно положительное число на другое, то мы получим также положительное число. Зная этот факт, мы можем сказать, что от числа множителей это не зависит – результат умножения любого числа положительных чисел есть число положительное. А что же такое степень, как не результат умножения чисел? Тогда для любой степени a n с положительным основанием и натуральным показателем это будет верно.

Также очевидно, что степень с основанием, равным нулю, сама есть ноль. В какую бы степень мы не возводили ноль, он останется им.

Вспомним, как правильно умножать отрицательные числа: произведение a · a равно произведению модулей, а, следовательно, оно будет положительным числом. Тогда и степень a 2 · m также положительны.

Тогда

7. Далее разберем следующее свойство, формулировка которого такова: из двух степеней, имеющих одинаковый натуральный показатель, больше та, основание которой больше (и наоборот).

8. Нам осталось доказать последнее свойство: если у нас есть две степени, основания которых одинаковы и положительны, а показатели являются натуральными числами, то та из них больше, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше.

Докажем эти утверждения.

Пример с конкретными числами: 3 7 > 3 2

Основные свойства степеней с целыми показателями

Для степеней с целыми положительными показателями свойства будут аналогичны, потому что целые положительные числа являются натуральными, а значит, все равенства, доказанные выше, справедливы и для них. Также они подходят и для случаев, когда показатели отрицательны или равны нулю (при условии, что само основание степени ненулевое).

Таким образом, свойства степеней такие же для любых оснований a и b (при условии, что эти числа действительны и не равны 0 ) и любых показателей m и n (при условии, что они являются целыми числами). Запишем их кратко в виде формул:

1. a m · a n = a m + n

2. a m : a n = a m − n

3. ( a · b ) n = a n · b n

4. ( a : b ) n = a n : b n

Доказательства этих свойств в данном случае несложные. Нам потребуется вспомнить, что такое степень с натуральным и целым показателем, а также свойства действий с действительными числами.

Условия: p = 0 или натуральное число; q – аналогично.

( a 0 ) q = 1 q = 1 a 0 · q = a 0 = 1

Следовательно, ( a 0 ) q = a 0 · q

Для q = 0 все точно так же:

( a p ) 0 = 1 a p · 0 = a 0 = 1

Вспомним доказанное выше свойство частного в степени и запишем:

1 a p q = 1 q a p q

Остальные свойства степени можно доказать аналогичным образом, преобразовав имеющиеся неравенства. Подробно останавливаться мы на этом не будем, укажем только сложные моменты.

Тогда неравенство можно преобразовать следующим образом:

Запишем правую и левую части в виде разности и выполним необходимые преобразования:

Последнее свойство степеней с целыми показателями доказывается аналогично свойству степеней с показателями натуральными.

Основные свойства степеней с рациональными показателями

В предыдущих статьях мы разбирали, что такое степень с рациональным (дробным) показателем. Их свойства такие же, что и у степеней с целыми показателями. Запишем:

Согласно тому, что из себя представляет степень с дробным показателем, получим:

Свойства корня позволят нам вывести равенства:

a m 1 · m 2 n 1 · n 2 · a m 2 · m 1 n 2 · n 1 = a m 1 · n 2 · a m 2 · n 1 n 1 · n 2

Из этого получаем: a m 1 · n 2 · a m 2 · n 1 n 1 · n 2 = a m 1 · n 2 + m 2 · n 1 n 1 · n 2

a m 1 · n 2 · a m 2 · n 1 n 1 · n 2 = a m 1 · n 2 + m 2 · n 1 n 1 · n 2

Показатель степени можно записать в виде:

m 1 · n 2 + m 2 · n 1 n 1 · n 2 = m 1 · n 2 n 1 · n 2 + m 2 · n 1 n 1 · n 2 = m 1 n 1 + m 2 n 2

Это и есть доказательство. Второе свойство доказывается абсолютно так же. Запишем цепочку равенств:

Доказательства остальных равенств:

a · b m n = ( a · b ) m n = a m · b m n = a m n · b m n = a m n · b m n ; ( a : b ) m n = ( a : b ) m n = a m : b m n = = a m n : b m n = a m n : b m n ; a m 1 n 1 m 2 n 2 = a m 1 n 1 m 2 n 2 = a m 1 n 1 m 2 n 2 = = a m 1 m 2 n 1 n 2 = a m 1 · m 2 n 1 n 2 = = a m 1 · m 2 n 2 · n 1 = a m 1 · m 2 n 2 · n 1 = a m 1 n 1 · m 2 n 2

Используем свойство корней и выведем: a m n b m n

Рациональные числа p и q можно привести к общему знаменателю и получить дроби m 1 n и m 2 n

Их можно переписать в следующем виде:

a m 1 n a m 2 n a m 1 n > a m 2 n

Тогда можно сделать преобразования и получить в итоге:

a m 1 n a m 2 n a m 1 n > a m 2 n

Основные свойства степеней с иррациональными показателями

1. a p · a q = a p + q

2. a p : a q = a p − q

3. ( a · b ) p = a p · b p

4. ( a : b ) p = a p : b p

Таким образом, все степени, показатели которых p и q являются действительными числами, при условии a > 0 обладают теми же свойствами.

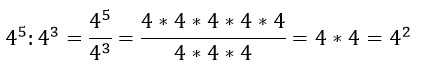
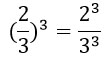
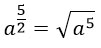
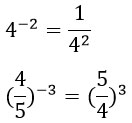
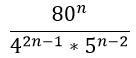
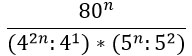
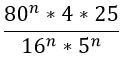
Источник