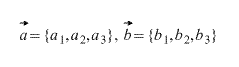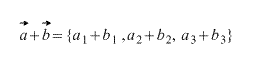Что такое векторная сумма
Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор.
Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор
Покоординатное сложение векторов.
Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:
В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.
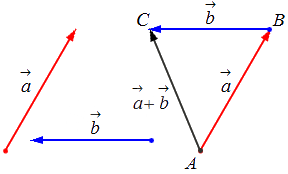
Теперь перейдем к геометрическому смыслу сложения двух векторов:
При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:
Правило параллелограмма. Сложение векторов по правилу параллелограмма.
Процедура сложения векторов по правилу параллелограмма заключается в следующем:
Правило треугольника. Сложение векторов по правилу треугольника.

Сложение векторов по правилу треугольника заключается в следующем:
Тригонометрический способ. Сложение векторов тригонометрическим способом.
Сила 1 равна 5кН и воздействует на тело в направлении, на 80 o отличающемся от направления действия второй силы, равной 8 кН.
Результирующая сила вычисляется следующим образом:
Угол между результирующей силой и первой силой равен:
А угол между второй и результирующей силой можно посчитать следующим образом: as
Он-лайн калькулятор сложения векторов.
Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.
Консультации и техническая
поддержка сайта: Zavarka Team
Сложение и вычитание векторов
Существование: Имеем два следующих случая:
Из данного выше построения сразу же будет следовать единственность данного вектора.
Сумма векторов. Сложение векторов. Правило треугольника
Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.
Такая операция выполняется по правилу многоугольника.
Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
\( \vec + \vec = \left( <
Отметим несколько свойств сложения двух векторов:
Для произвольного вектора \( \overrightarrow \) выполняется равенство
Для произвольных точек \( A,\ B\ и\ C \) справедливо следующее равенство
Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.
Разность векторов. Вычитание векторов
Длина нулевого вектора равна нулю:
\( \left| \vec <0>\right| = 0 \)
Умножение вектора на число
Определение Произведением вектора \( \overrightarrow
Длина вектора \( \overrightarrow
Векторы \( \overrightarrow
Операции над векторами и их свойства: сложение и умножение
Прежде чем приступить к тематике статьи, напомним основные понятия.
Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.
Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.
Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.
Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.
Сложение двух векторов
Геометрически сложение векторов выглядит так:
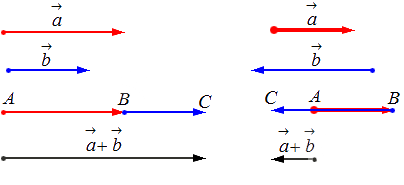
— для неколлинеарных векторов:
— для коллинеарных (сонаправленных или противоположнонаправленных) векторов:
Сложение нескольких векторов
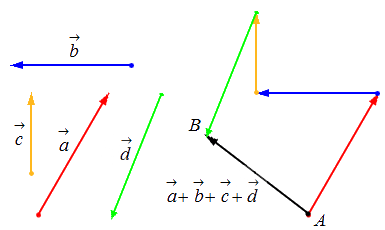
Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.
Геометрически оно выглядит следующим образом:
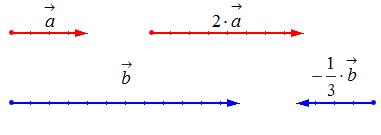
Умножение вектора на число
Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:
Свойства операций над векторами
Описанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.
Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.
Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.
Сумма векторов: графический метод, примеры, решенные упражнения.
Содержание:
В векторная сумма это операция сложения между векторами, которая приводит к другому вектору. Векторы характеризуются величиной, а также направлением и смыслом. Следовательно, в общем случае невозможно сложить их, как это было бы со скалярными величинами, то есть путем сложения чисел.
Вектор, полученный из суммы нескольких векторов, называется результирующий вектор. В механике говорят о Равнодействующая сила, которая представляет собой векторную сумму всех сил, действующих на тело. Эта равнодействующая эквивалентна множеству или системе сил.
Чтобы полностью указать вектор суммы, необходимо указать величину и единицу, направление и смысл.
Важно отметить, что при сложении векторов они должны представлять одну и ту же физическую величину, поэтому векторная сумма является однородной операцией. Это означает, что мы можем добавлять одну силу к другой, но не силу со смещением, поскольку результат не имеет смысла.
Для нахождения результирующего вектора доступны несколько методов: графический и аналитический. Чтобы найти векторные суммы с помощью графических методов, мы начнем с простого представления вектора, а именно с ориентированного сегмента или стрелки, подобного этому:
Векторы обозначаются жирными буквами в печатном тексте или стрелкой над буквой, чтобы отличать их от соответствующих величин или скалярных величин. Например, величина вектора vЭто просто v.
Графический метод сложения векторов
Чтобы добавить более двух копланарных векторов, полигональный метод или метод траверса, который состоит из трансляции себя параллельно каждому из векторов слагаемых. Характерной чертой векторов является то, что они инвариантны относительно сдвига, поэтому мы будем использовать это свойство для определения суммы.
Мы начинаем с любого из векторов, так как сложение векторов коммутативно и порядок слагаемых не влияет на сумму. Затем переводится второй вектор, сопоставляя его начало с концом первого.
Затем он переносится к следующему вектору и помещается следующим, следуя той же процедуре, которая заключается в совпадении начала координат с концом предыдущего. Продолжайте таким образом, пока не будет установлен последний вектор.
пример
Возьмем для примера сумму двух векторов или Y v показано на рисунке выше.
Начиная с вектора или, переехал в вектор v чтобы его начало совпадало с концом первого. Результирующий вектор ш взят из происхождения или до конца v, образуя трехстороннюю фигуру: треугольник. Поэтому в этом частном случае процедура называется метод треугольника.
Обратите внимание на важную деталь: величина или модуль результирующего вектора не является суммой модулей добавленных векторов. Фактически, это почти всегда меньше, если векторы не параллельны.
Посмотрим, что происходит в этом случае ниже.
Частный случай: сумма параллельных векторов
Описанный метод применим и к частному случаю, когда векторы параллельны. Рассмотрим следующий пример:
Оставлено вектору v в исходном положении и переводится в вектор или таким образом, что его происхождение совпадает с концом v. Теперь нарисован вектор, начиная с начала координат v и заканчивает конец или.
Результирующий вектор имеет максимальный модуль, если слагаемые образуют угол 0º друг с другом, как в примере. Если векторы расположены под углом 180º друг к другу, то результирующий вектор имеет минимальный модуль.
Примеры сложения векторов
— Смещения
Велосипедист проезжает сначала 3 км в северном направлении, а затем 4 км на запад. Ваше перемещение, которое мы называем р, легко найти с помощью метода треугольника плюс система отсчета, где отмечены стороны света:
Шаги к векторному сложению
— Начальная точка совпадает с началом системы отсчета.
-По осям координат выбран масштаб, который в данном случае составляет 1 см = 1 км.
-Первое смещение нарисовано в масштабе d1.
-Следующий d1 второе смещение нарисовано d2, также в масштабе.
-Размерр измеряется градуированной линейкой, легко проверить, что R = 5.
-Наконец, угол, который р форма по горизонтали измерена с помощью транспортира и составляет θ = 37 0
— Результирующая скорость
Пловец хочет пересечь реку и для этого плывет со скоростью 6 км / ч перпендикулярно берегу, но его отклоняет течение со скоростью 4 км / ч.
Чтобы узнать его итоговую скорость, добавляются векторы скорости пловца, изображенного вертикально, и вектора скорости, отображаемого горизонтально.
Графическим методом получается результирующая скорость. vр:
Отклонение, которое испытывает пловец, можно рассчитать следующим образом:
θ = arctg (4/6) = 33,7º вправо от начального направления
Величина его скорости увеличивается благодаря тому, что скорость реки складывается векторно. Его можно найти, аккуратно установив масштаб, как в примере выше.
Или с помощью тригонометрических соотношений 33,7º:
vр = 4 / sin 33,7º = 7,21 км / ч
Упражнение решено
На частицу действуют следующие силы, величины которых указаны ниже:
Найдите равнодействующую силу.
Решение
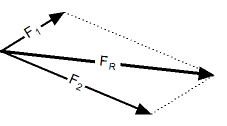
Мы можем складывать графически, начиная с любого из векторов, поскольку векторная сумма коммутативна.
На рисунке A мы начали с F1. Устанавливая масштаб, с помощью линейки и квадрата переносятся другие векторы, чтобы расположить их один за другим.
Вектор Fр направлено от происхождения F1 до конца F4. Его величина составляет 5,2 Н, и он образует угол 26,5 ° по отношению к горизонту.
Многоугольники разные, но результат тот же. Читатель может провести тест, снова изменив порядок векторов.
Сложение векторов: длина суммы векторов и теорема косинусов
Определения скалярного произведения векторов через угол между ними
Сложение векторов, заданных координатами (при сложении одноимённые координаты складываются) даёт возможность узнать, как расположен относительно начала координат вектор, являющийся суммой слагаемых векторов. Подробно эти две операции разбирались на уроке «Векторы и операции над векторами».
При сложении векторов для нахождения длины суммы векторов используется теорема косинусов. Пусть 




где 

Поэтому для сложения векторов и определения длины суммы векторов нужно извлечь квадратный корень из каждой части равенства, тогда получится формула длины:

В случае вычитания векторов (







косинусы смежных углов равны по абсолютной величине (величине по модулю), но имеют противоположные знаки.
Перейдём к примерам.
Пример 1. Векторы 






Решение. Из элементарной тригонометрии известно, что 
Шаг 1. Выполняем сложение векторов. Находим длину суммы векторов, поставляя в формулу длины косинус угла, смежного с углом между векторами:
Шаг 2. Выполняем вычитание векторов. Находим длину разности векторов, подставляя в формулу косинус «изначального» угла:
Выполнить сложение и вычитание векторов самостоятельно, а затем посмотреть решение
Пример 2. Векторы 






Пример 3. Даны длины векторов 


Шаг 1. По теореме косинусов составляем уравнение, чтобы найти косинус угла, смежного с углом между векторами и находим его:
Не забываем, что косинус смежного угла получился со знаком минус. Это значит, что косинус «изначального» угла будет со знаком плюс.
Шаг 2. Выполняем вычитание векторов. Находим длину разности векторов, подставляя в формулу косинус «изначального» угла:
Пример 4. Даны длины векторов 


Шаг 1. По теореме косинусов составляем уравнение, чтобы найти косинус «изначального» угла (задача обратная по отношению к примеру 1) и находим его:
Шаг 2. Меняем знак косинуса и получаем косинус смежного угла между 

Шаг 3. Выполняем сложение векторов. Находим длину суммы векторов, подставляя в формулу косинус смежного угла:
Пример 5. Векторы 




Пример 6. Какому условию должны удовлетворять векторы 

1) длина суммы векторов равна длине разности векторов, т. е. 
2) длина суммы векторов больше длины разности векторов, т. е. 
3) длина суммы векторов меньше длины разности векторов, т. е. 
Находим условие для первого соотношения. Для этого решаем следующее уравнение:
То есть, для того, чтобы длина суммы векторов была равна длине их разности, необходимы, чтобы косинус угла между ними и косинус смежного ему угла были равны. Это условие выполняется, когда углы образуют прямой угол.
Находим условие для второго соотношения. Решаем уравнение:
Найденное условие выполняется, когда косинус угла между векторами меньше косинуса смежных углов. То есть, чтобы длина суммы векторов была больше длины разности векторов, необходимо, чтобы углы образовали острый угол (пример 1).
Находим условие для третьего соотношения. Решаем уравнение:
Найденное условие выполняется, когда косинус угла между векторами больше косинуса смежных углов. То есть, чтобы длина суммы векторов была меньше длины разности векторов, необходимо, чтобы углы образовали тупой угол.