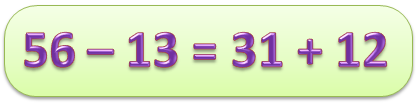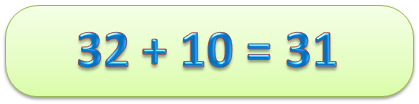Что такое верные равенства

Символ равенства (=) — это когда два коротких отрезка записаны горизонтально и параллельны друг другу. Используем его при сравнении двух одинаковых чисел:

Чтобы ребенку было легче запомнить схожие между собой знаки, можно применить игровой метод. Для этого нужно сравнить числа и определить в каком порядке они стоят. Далее ставим одну точку у наименьшего числа и две — рядом с наибольшим. Соединяем точки и получаем нужный знак. Вот так просто:

Равенство и неравенство

Что такое равенство в математике — это когда одно подобно по количеству другому и между ними можно поставить знак =.

Для примера посмотрим на картинку с изображением геометрических фигур. Справа и слева количество одинаковое, значит можно поставить символ «равно».

Наглядный пример неравенства изображен на картинке ниже. Слева видим три фигуры, а справа — четыре. При этом мы знаем, что три не равно четырем или еще так: три меньше четырех.

Урок в школе зачастую проходит перед учебником, тетрадью и доской. Дома же можно использовать компьютер и некоторые задания выполнять в онлайн-формате. Как найти знаки на клавиатуре? Ответ на картинке:

Типы неравенств

Источник

интернет проект BeginnerSchool.ru

Сайт для детей и их родителей

Числовые равенства и неравенства

Числовые равенства

Чтобы получить запись, называемую числовым равенством, надо два числовых выражения соединить знаком равенства (=).

Представленный пример является верным числовым равенством, но числовое равенство может быть неверным:

Давайте разберем свойства числовых равенств.

(12 + 3) = (9 + 6)

12 + 3 = 15 и 9 + 6 = 15

Равенство верно, теперь проверим свойство

(12 + 3) + (5 – 2) = (9 + 6) + (5 – 2)

15 + (5 – 2) = 15 + (5 – 2)

18 = 18

В обоих случаях равенства верны

Проверим это свойство на предыдущем примере заменив действие сложение на вычитание:

(12 + 3) – (5 – 2) = (9 + 6) – (5 – 2)

15 + (5 – 2) = 15 + (5 – 2)

12 = 12

Как мы видим равенство верно.

Проверим и это свойство:

(75 – 3) = (15 + 57)

75 – 3 = 72 и 15 + 57 = 72 это равенство верно

(75 – 3) · (10 – 2) = (15 + 57) · (10 – 2)

72 · (10 – 2) = 72 · 8 = 576

576 = 576

Проверим это свойство:

(12 + 3) : (5 – 2) = (9 + 6) : (5 – 2)

15 : 3 = 15 : 3

5 = 5

Что и требовалось доказать.

Числовые неравенства

(10 + 25)

Числовые неравенства также могут быть верными и неверными:

(25 – 5) : 5 > 10 – это неравенство неверно

(25 – 5) : 5

Спасибо, что Вы с нами!

Оставляйте пожалуйста комментарии в форме ниже

Источник

Что такое числовые выражения, равенства, неравенства и уравнения

Выражение

Числовое выражение — это числа, соединённые знаками арифметических действий: сложение, вычитание, умножение и деление.

Найти значение числового выражения — это значит выполнить все указанные арифметические действия и получить конкретное число.

Кроме арифметических действий выражения могут содержать скобки, которые влияют на порядок действий при решении выражения.

Пример 1:

Равенство

Равенства — это числа или выражения, соединённые знаком = (равно).

Равенство считается верным, если числа или числовые выражения слева и справа от знака =, имеют равное значение.

Равенство считается неверным, если числа или числовые выражения слева и справа от знака =, не равны (≠).

При решении равенств соблюдается следующий порядок действий:

Пример 2:

1) 5 = 7 — равенство неверно, так как 5 ≠ 7.

2) 36 : 2 = 6 • 3 — равенство верно, так как:

3) 48 + 9 = 54 — 1 — равенство неверно, так как:

Неравенство

Пример 3:

1) 5 > 7 — неравенство неверно, так как 5

3) 4 + 5 • 6 > (4 + 5) • 6 — неравенство неверно, так как:

Уравнение

Уравнение — это равенство, которое содержит неизвестное число, обозначенное какой-либо латинской буквой: x, y, a, b, z, d и т.д.

Корень уравнения — это число, при подставлении котрого вместо буквы в равенство делает это равенство верным.

Решить уравнение — это значит найти все возможные корни уравнения.

Порядок и правила решения уравнений зависят от того, к какому типу они относятся:

Источник