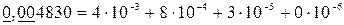Что такое верные значащие цифры
Что такое верные значащие цифры
Раздел 1. Приближенные числа и действия над ними
1.1 Виды погрешностей при приближенных вычислениях
Точное решение некоторых математических задач невозможно получить классическими методами, или это решение может быть получено в таком сложном виде, что неприемлемо для дальнейшего практического использования. Кроме того, точное решение задачи может потребовать очень большого количества (от нескольких десятков до многих миллиардов) действий. В таких случаях прибегают к приближенным и численным методам решения.
Появление компьютеров значительно расширило область применения этих методов. В настоящее время трудно себе представить инженера, не владеющего компьютером и методами приближённых вычислений.
Заметим, что любой компьютер способен запоминать большие, но конечные массивы чисел и производить над ними арифметические операции и сравнения с большой, но конечной скоростью. То есть машина способна выполнять очень большое, но конечное число операций. Поэтому при работе на компьютере можно использовать только те математические модели, которые описываются конечным набором чисел, и использовать только конечные последовательности арифметических действий.
Математическими моделями различных явлений служат функции, производные, интегралы, дифференциальные уравнения и т.п. При работе на компьютере эти исходные модели следует заменить такими, которые описываются конечными наборами чисел с указанием конечной последовательности действий для их обработки. Для этого функцию заменяют таблицей, определённый интеграл — суммой и т.д. Кроме того, вычислительная машина обладает конечной памятью и может оперировать с числами конечной длины, поэтому промежуточные результаты округляются. В результате этого даже точный метод с конечным числом действий становится приближенным.
Таким образом, решение, полученное численным методом, является приближенным.
Причинами появления погрешностей являются:
Погрешность решения, вызванная первыми двумя причинами, называется неустранимой — она не зависит от математика.
Погрешность метода возникает потому, что численным методом, как правило, решается не исходная задача, а более простая. Кроме того, обычно численный метод основан на бесконечном процессе, который приходится обрывать на некотором шаге.
Большинство численных методов зависит от одного или от нескольких параметров. Выбор параметров метода позволяет регулировать погрешность метода.
Погрешность округлений не должна быть существенно больше погрешности метода. А погрешность метода целесообразно выбирать в 2-5 раз меньше неустранимой погрешности.
1.2 Приближенные числа
Определение 1.2. Относительной погрешностью приближенного числа a * называется величина:
Любое число d ( a * ) , удовлетворяющее неравенству
Верные и сомнительные цифры приближенного значения числа.
Значащие цифры приближенного значения числа
При вычислениях часто трудно указать наряду с приближенными значениями их погрешности. А в различных справочниках указывать погрешности приближенных данных неудобно, неэкономично. Поэтому при записи приближенных значений чисел требуют, чтобы по этой записи можно было определить границу абсолютной погрешности приближения. Для этого вводится понятие верной и сомнительной цифр приближенного значения числа.
Определение: Цифра называется верной, если граница абсолютной погрешности данного приближенного значения числа не превосходит (£) единицы того разряда, в котором записана эта цифра. В противном случае цифра называется сомнительной.
Пример: Определить верные и сомнительные цифры в приближенном значении числа:
1. х = 35,4 ± 0,08
Вывод: Если в записи приближенного значения числа какая-то цифра – верная, то и все предшествующие ей цифры так же являются верными.
2. х = 9,846 ± 0,04
Цифра 4 в 0,01; h = 0,04 £ 0,01; 4 – сомнительная цифра;
Цифра 8 в 0,1; h = 0,04 £ 0,1; 8 – верная цифра;
Следовательно, 9 – верная цифра.
3. х = 945,673 ± 0,03
Цифра 3 в 0,001; h = 0,03 £ 0,001; 3 – сомнительная цифра;
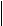
Цифра 7 в 0,01; h = 0,03 £ 0,01; 7 – сомнительная цифра;
Цифра 6 в 0,1; h = 0,03 £ 0,1; 6 – верная цифра;
Следовательно, 5, 4, 9 – верные цифры.
При записи приближенных чисел принято соблюдать следующие правила.
Правила записи приближенных чисел:
Пример: Записать правильно приближенное значение числа:
1. х = 950,031 ± 0,04
Следовательно, 0, 5, 9 – верные цифры.
х » 950,0 (правила 1, 2)
2. х = 0,075 ± 0,000005
х » 0,07500 (правила 1, 2)
3. х = 746000000 ± 5000
Следовательно, 0, 6, 4, 7 – в. ц.
х » 74600 × 10 4 (правила 1, 3)
Если приближенное значение числа дано без указания границы абсолютной погрешности, то ее можно определить по записи этого приближенного значения, используя определение верной и сомнительной цифр приближенного значения числа.
Пример:
1. Указать абсолютную погрешность приближенного числа а = 3,14.
Решение:
Дата добавления: 2017-01-29 ; просмотров: 40183 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Значимые цифры: правила, примеры, решенные упражнения
Содержание:
А что происходит, когда число целое? Это означает, что он известен с максимально возможной точностью, другими словами, он имеет бесконечную точность. Например, при подсчете людей, животных или таких предметов, как книги и телефоны, результатом будет точное целое число.
Если мы скажем, что в кинотеатре 110 человек смотрят фильм, это точное число, ни много, ни мало, и оно состоит из трех значащих цифр.
Значительные числа обрабатываются по некоторым простым правилам, которые запоминаются после небольшой практики, как мы увидим дальше.
Правила определения значащих цифр числа
Правило 1
Начальные нули не считаются значащими цифрами, поэтому 0,045 и 4,5 имеют две значащие цифры, поскольку они начинают отсчет слева и начиная с первой ненулевой цифры.
Правило 2
Нули после (справа) первой значащей цифры действительно считаются значащей цифрой (если это оправдано точностью измерительного прибора).
Наконец, нули в середине также считаются значащей цифрой.
Правило 3
Для чисел, записанных в экспоненциальном представлении, все цифры в мантиссе значимы, а показатель степени не влияет на точность.
Правило 4
При выполнении операций с десятичными знаками, например при вычислении площадей или других подобных операций, результат должен иметь такое же количество значащих цифр, что и количество с наименьшим количеством значащих цифр, участвовавших в операции. Это правило действует для любых арифметических операций.
Правило 5
Знак числа не влияет на количество его значащих цифр.
Мы сразу же увидим некоторые примеры этого и всех других правил.
Примеры
Пример 1
Найдите, сколько значащих цифр в каждом из этих чисел.
Ответы
а) 876 имеет 3 значащих цифры.
б) 1000,68 имеет 6 значащих цифр, поскольку нули в середине считаются как таковые.
c) Вместо 0,00005026 имеется 4 значащих цифры. Обратите внимание, что 5 нулей слева от 5 не считаются значащими цифрами, тогда как 0 между 5 и 2 считается.
г) 4.8 имеет 2 значащих цифры.
Пример 2
Обычно измерения проводят с помощью измерительных инструментов, таких как рулетки, часы, термометры, весы и т. Д. Со сколькими значащими цифрами мы должны указывать количества, которые мы измеряем таким образом?
Ответить
Это зависит от оценки инструмента, которым он измеряется. Возьмем пример: измерьте внешний диаметр трубы с помощью градуированной линейки и штангенциркуля.
Он более точен, чем градуированная линейка, потому что с его помощью мы можем узнать более значащие числа определенной длины.
Вот почему нет смысла сообщать периметр, скажем, 35,88 см, если мы измеряем его рулеткой, поскольку этот инструмент недостаточно точен, чтобы указать такое количество значащих цифр.
Оценка рулетки A определяется по:
Пример 3
Сколько значащих цифр в показании цифрового термометра?
Ответить
Термометр на рисунке показывает трехзначные показания температуры. Однако в показанном измерении 36,6 ºC только первые две цифры слева направо являются точными, поскольку на десятичную дробь влияет погрешность оценки прибора, которая обычно указывается на задней стороне прибора или на ваше руководство по эксплуатации.
Обычно для представленного типа цифрового прибора погрешность оценки составляет 0,1 ºC. Этого достаточно, чтобы быть уверенным, что у вас нет температуры.
Правила округления чисел
При использовании калькулятора для выполнения расчетов с полученными измерениями некорректно давать результат, используя все цифры, которые появляются на экране.
Сохраняются только те, которые точно известны, поскольку только они имеют истинное значение. Затем необходимо округлить результаты, чтобы они соответствовали количеству точно известных цифр. Вот эти правила:
-Если число, следующее за цифрой, которую необходимо скрыть, является равно или больше 5, к этой цифре добавляется 1.
Например, при округлении 3,786 до двух десятичных знаков мы хотим сохранить числа до 8. Поскольку число, следующее за (6), больше 5, 8 становится 8 + 1 = 9, и число остается как 3.79.
-Когда число, следующее за цифрой, которую необходимо сохранить, менее 5, цифра останется прежней.
Если мы хотим округлить 1,27924, чтобы у него было только 3 десятичных разряда, это достигается путем достижения 9, за которым следует 2. Поскольку 2 меньше 5, эти десятичные дроби исчезают, а округленное число остается 1,279.
Упражнение решено
Обеденный стол имеет форму и размеры, указанные на прилагаемом рисунке. Вам предлагается рассчитать его площадь по правилам работы со значащими цифрами.
Решение
Зона стола может быть разделена на центральную прямоугольную зону и два полукруга, по одному с каждой стороны, которые вместе составляют один полный круг.
Мы будем называть A1 к площади прямоугольника, задаваемой:
К1 = основание × высота = 2,5 м x 1,0 м = 2,5 м 2
Со своей стороны, площадь круга, равная площади 1 полукруга, умноженной на 2, равна:
Диаметр любого из полукругов составляет 1,0 м, поэтому радиус равен 0,50 м. Диаметр также можно использовать напрямую для расчета площади, в этом случае:
К2 = (π × диаметр 2 ) / 4
К2 = [π x (1,0 м) 2 ] / 4 = 0,785398163 м 2
Были использованы все цифры, предоставленные калькулятором. Теперь добавляем A1 уже2 для общей площади стола A:
A = (2,5 + 0,785398163) м 2 = 3,285398163 м 2
Поскольку размеры таблицы известны до двух значащих цифр, не имеет смысла выражать результат со всеми десятичными знаками, указанными калькулятором, который никогда не дает количество значащих цифр в результате.
Что вам нужно сделать, так это округлить область так, чтобы в ней было такое же количество значащих цифр, что и размеры таблицы, то есть 2. Таким образом, окончательный результат будет представлен следующим образом:
Ссылки
Материальное завоевание Новой Испании: этапы и последствия
Граница абсолютной погрешности
Вычислительная математика. Граница абсолютной погрешности
Абсолютная погрешность приближенного значения числа, граница абсолютной погрешности, верные и значащие цифры числа
Верные и значащие цифры числа. Округление чисел.
Наша система счета или счисления называется десятичной системой счисления, а 10 – основанием этой системы:
разряд единиц, разряд десятков, разряд сотен и т.д. Аналогично, разряды десятичных дробей: десятые, сотые, тысячные и т.д.
В приближенном числе различают верные и сомнительные цифры. Цифра какого-либо разряда приближенного числа а считается верной в широком смысле, если граница абсолютной погрешности числа а не превосходит единицы того разряда, в котором записана эта цифра.
Если же граница абсолютной погрешности больше единицы какого-либо разряда, то цифра этого разряда и все цифры, расположенные справа от нее считаются сомнительными. Граница абсолютной погрешности ∆а находится непосредственно по записи приближенного значения а числа х.
Например:
Приближенное значение 24,5
Граница абсолютной погрешности 0,3
Приближенное значение 375
Граница абсолютной погрешности 20
Когда рассматриваем верные цифры в широком смысле, то достаточно посмотреть на границу абсолютной погрешности и взять цифры приближенного числа, которые на разряд больше, чем граница абсолютной погрешности.
Цифра какого-либо разряда приближенного числа а считается верной в строгом смысле, если граница абсолютной погрешности числа а не превосходит половины единицы того разряда, в котором записана эта цифра. Если же граница абсолютной погрешности больше половины единицы какого-либо разряда, то цифра этого разряда и все цифры, расположенные справа от нее считаются сомнительными.
В числах, полученных в результате измерений или вычислений и используемых при расчётах в качестве исходных данных, а также в десятичной записи приближенного значения числа, все цифры должны быть верными.
Значащими цифрами приближенного числа, выраженного десятичной дробью считаются все верные цифры этой дроби, кроме нулей, стоящих перед первой цифрой (слева направо), отличной от нуля.
Например:
Приближенное число 10,408 имеет 5 значащих цифр, так как крайняя слева цифра числа отлична от нуля (она равна 1)
Приближенное число 0,01104 имеет 4 значащие цифры:1, 1, 0, 4. Два нуля, стоящие слева от 1 не считаются значащими цифрами
Приближенное число 0,030 имеет 2 значащие цифры: 3 и 0 справа, по правилу два нуля, стоящие слева от цифры 3, не относятся к значащим.
Значащими цифрами приближенного целого числа считаются все его цифры, кроме нулей, поставленных взамен отброшенных или
Например: Частное
Число 6000 имеет 3 значащие цифры, так как один последний нуль поставлен вместо отброшенной цифры (единицы).
Округление чисел. При округлении числа а его заменяют числом а1 с меньшим количеством значащих цифр. Абсолютная величина разности
| а – а1 | называется погрешностью округления.
При применении этого правила погрешность округления не превосходит половины единицы десятичного разряда, определяемого последней оставленной значащей цифрой.
Округление приближенных значений чисел с сохранением в записи только верных цифр производится до разряда, в котором записана первая справа верная цифра.
Например:
Округлите до первого справа верного разряда приближенные значения данных чисел:
Граница абсолютной погрешности 0,05 (разряд – сотые) цифры справа налево:1 – сомнительная, 8 – сомнительная, 2 – сомнительная, 3 – верная цифра 3
Десятичная запись приближенных чисел. Значащая цифра. Верные значащие цифры. Округление чисел. Связь между числом верных знаков и погрешностью числа
Десятичная запись приближенных чисел. Значащая цифра. Верные значащие цифры. Известно, что любое положительное число a может быть представлено в виде конечной или бесконечной десятичной дроби
,
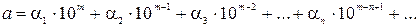
Например, в десятичной записи числа 2857,697
,
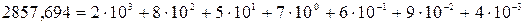
цена разряда, в котором стоит цифра 8, есть 10 3- 2 + 1 = 100; цифра 7 –
На практике обычно имеют дело с приближенными числами, представляющими собой конечные десятичные дроби
.
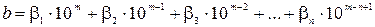
Все сохраняемые десятичные знаки βi (i = 1, 2, 3,…, n) называются значащими цифрами числа b, причем возможно, что некоторые из них равны нулю (за исключением β1). При позиционном отображении числа b в десятичной системе счисления нередко приходится вводить лишние нули в начале или в конце числа, например
.
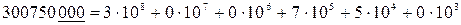
Такие нули (в приведенных примерах они подчеркнуты) не считаются значащими числами.
Определение 1. Значащей цифрой приближенного числа называются всякая цифра, отличная от нуля, и нуль, если он содержится между значащими цифрами или является представителем сохраненного десятичного разряда. Все остальные нули, входящие в состав приближенного числа и служащие лишь для обозначения десятичных разрядов его других цифр, не причисляются к значащим цифрам.
У Данилиной А.И. [1] дается несколько иное определение. Значащими цифрами называются все его цифры, кроме нулей, стоящих левее первой отличной от нуля цифры.
Нули в конце числа – всегда значащие цифры (в противном случае их не пишут). Например, числа 0,00207 и 54,700 имеют соответственно 3 и 5 значащих цифр.
Определение 2. n первых значащих цифр приближенного числа являются верными, если абсолютная погрешность этого числа не превышает половины единицы разряда, выражаемого n – й значащей цифрой (αn), считая слева направо, т. е. выполняется неравенство
. (2)
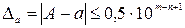
Например, для точного числа A = 47,96 число a = 48,00 является приближением с тремя верными знаками, так как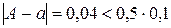 
(здесь m =1; n = 3).
Если неравенство (2) не выполняется, то цифру αn называют сомнительной.
У Копченовой Н.В. [3] приводится более простое правило определения числа верных знаков приближенного числа.
Замечание. При выполнении неравенства (2) количество верных значащих цифр понимается в узком смысле. Наряду с таким понятием используется понятие верных значащих цифр в широком смысле.
Число a является приближением точного числа A с n верными знаками в широком смысле, если абсолютная погрешность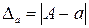 
не превышает единицы десятичного разряда, в котором стоит n-я значащая цифра αn приближенного числа, т. е. выполняется неравенство
. (3)
Например, для точного числа A = 457,9678 число a = 457,967 является приближением с шестью верными знаками, так как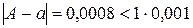 
(здесь m =2; n = 6).
Округление чисел. Часто возникает необходимость в округлении приближенного или точного числа a, т. е. в замене его числом a1 с меньшим количеством значащих цифр. При этом сохраняют одну или несколько цифр, считая слева направо, и отбрасывают все последующие. Число a1 выбирают так, чтобы погрешность округления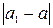 
была минимальной.
Наиболее употребительными являются следующие правила округления.
1. Если отбрасываемые цифры составляет число, большее половины единицы последнего оставляемого разряда, то последняя оставляемая цифра увеличивается на единицу.
2. Если отбрасываемые цифры составляет число, меньшее половины единицы последнего оставляемого разряда, то оставляемые цифры не изменяются.
3. Если отбрасываемые цифры составляет число, равное половине единицы последнего оставляемого разряда, то последняя оставляемая цифра увеличивается на единицу, если она нечетная, и остается без изменения, если она четная (правило четной цифры).
Примеры. Округлить до трех цифр следующие числа:
а) a = 13,8658. Согласно правилу 1, получим a1 = 13,9;
б) a = 148,358. Согласно правилу 2, получим a1 = 148;
в) a = 6,86500. Согласно правилу 3, получим a1 = 6,86;
г) a = 347,50. Согласно правилу 3, получим a1 = 348;
Точность приближенного числа зависит не от количества значащих цифр, а от количества верных значащих цифр. В случаях, когда приближенное число содержит излишнее количество неверных значащих цифр, прибегают к округлению. При этом руководствуются следующим практическим правилом:
При выполнении приближенных вычислений число значащих цифр промежуточных результатов не должно превышать числа верных цифр более чем на одну или две единицы. Окончательный результат может содержать не более чем одну излишнюю значащую цифру, по сравнению с верными.
Заметим, что абсолютная погрешность приближенного числа a1 после округления складывается из абсолютной погрешности числа a и погрешности округления
.
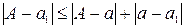
Связь между числом верных знаков и относительной погрешностью приближенного числа. Устанавливается на основе следующей теоремы (доказательство приведено в [2, с. 25-27]).
Теорема. Если положительное приближенное число a имеет n верных цифр в узком смысле, то относительная погрешность δ этого числа не превосходит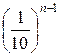 
, деленную на первую значащую цифру α1 данного числа,
т. е.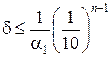 
.
Из этой теоремы вытекают два следствия.
Следствие 1. За предельную относительную погрешность числа a можно принять:
, (4)
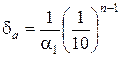
Следствие 2. Если число a имеет больше двух верных цифр т. е. n ≥ 2, то справедлива формула
. (5)
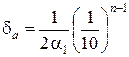
Замечание. Если приближенное число a имеет n верных цифр в широком смысле, то оценки (4) и (5) следует увеличить в два раза.
Пример 1. Какова относительная погрешность, если вместо числа π взять число a = 3,14?
Решение. В данном примере α1 = 3 и n = 3. Следовательно
.
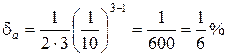
Пример 2. Сколько десятичных знаков взять при вычислении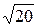 
с относительной погрешностью 0,1%?
Вышеприведенная теорема дает возможность по числу верных знаков приближенного числа
(6)
определить его относительную погрешность δ.
Из формулы относительной погрешности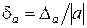 
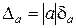
имеем
. (7)
Учитывая старший десятичный разряд Δa, легко установить количество верных знаков данного приближенного числа a. В частности, если
,
то из формул (6) и (7) находим
,
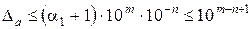
т. е. число a имеет n верных цифр в широком смысле. Аналогично, если
,
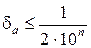
То число a имеет n верных цифр в узком смысле.
Пример 3. Приближенное число a = 24253 имеет относительную точность 1%. Сколько в нем верных цифр?
3. Погрешности суммы и разности. Потеря точности при вычитании близких чисел [1]
Погрешность суммы. Рассмотрим точные числа A1, A2,…, An и их приближенные значения a1, a2,…, an. Пусть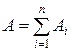 
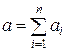
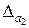
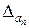
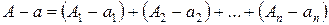
— сумма всех точных чисел, а 
— сумма их приближенных значений и известны абсолютные погрешности 
, 
,…, 
всех приближенных чисел. Необходимо оценить абсолютную погрешность суммы приближенных чисел.
.
Переходя к абсолютным величинам правой и левой частей записанного выражения и используя свойство абсолютных величин, получим
, т. е.
. (8)
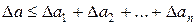
Следствие. За абсолютную погрешность алгебраической суммы приближенных чисел можно принять сумму абсолютных погрешностей этих чисел
. (9)
Из последней формулы следует, абсолютная погрешность суммы не может быть меньше абсолютной погрешности наименее точного слагаемого. Поэтому не имеет смысла сохранять излишние знаки и в более точных слагаемых. Отсюда при сложении чисел различной абсолютной точности поступают следующим образом:
1) выделяют число (или числа), имеющее наибольшую абсолютную погрешность;
2) остальные числа округляют по образцу выделенных, сохраняя один запасной десятичный знак;
3) производят сложение чисел, учитывая все сохраненных знаки;
4) полученный результат округляют на один знак.
Пример. Найти сумму приближенных чисел: 345,4; 0,348; 0,1834; 235,2; 11,75; 9,27; 0,0849; 0,0214; 0,000354, каждое из которых имеет все верные значащие цифры (в широком смысле).
Решение. 1) Выделяем числа наименьшей точности 345, 4 и 235,2, абсолютная погрешность которых может достигать 0,1.
2) Округляем остальные числа с точностью до 0,01: 0,35; 0,18; …;
3) Выполняя суммирование всех полученных чисел, получим
Округляя результат до 0,1 по правилу четной цифры, находим приближенное значение суммы 602,2.
Полная погрешность Δ результата складывается из трех слагаемых:
1) суммы погрешностей исходных данных
Дата добавления: 2019-01-14 ; просмотров: 1057 ; Мы поможем в написании вашей работы!