Что такое вершина в информатике 9 класс
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
§ 1.3. Графические информационные модели
Информатика. 9 класса. Босова Л.Л. Оглавление
Ключевые слова:
• схема
• карта
• чертёж
• график
• диаграмма
• граф
• сеть
• дерево
В графических информационных моделях для наглядного отображения объектов используются условные графические изображения (образные элементы), зачастую дополняемые числами, символами и текстами (знаковыми элементами). Примерами графических моделей могут служить всевозможные схемы, карты, чертежи, графики и диаграммы.
Схема — это представление некоторого объекта в общих, главных чертах с помощью условных обозначений. С помощью схем может быть представлен и внешний вид объекта, и его структура. Схема как информационная модель не претендует на полноту предоставления информации об объекте. С помощью особых приёмов и графических обозначений на ней более рельефно выделяется один или несколько признаков рассматриваемого объекта. Примеры схем приведены на рис. 1.5.
Рис. 1.5. Примеры схем, используемых на уроках физики, биологии, истории
Уменьшенное обобщённое изображение поверхности Земли на плоскости в той или иной системе условных обозначений даёт нам географическая карта.
Чертёж — условное графическое изображение предмета с точным соотношением его размеров, получаемое методом проецирования. Чертёж содержит изображения, размерные числа, текст. Изображения дают представления о геометрической форме объекта, числа — о величине объекта и его частей, надписи — о названии, масштабе, в котором выполнены изображения.
График — графическое изображение, дающее наглядное представление о характере зависимости одной величины (например, пути) от другой (например, времени). График позволяет отслеживать динамику изменения данных.
Диаграмма — графическое изображение, дающее наглядное представление о соотношении каких-либо величин или нескольких значений одной величины, об изменении их значений. Более подробно типы диаграмм и способы их построения будут рассмотрены при изучении электронных таблиц.
1.3.2. Графы
Если некоторые объекты изобразить вершинами, а связи между ними — линиями, то мы получим информационную модель в форме графа. Вершины графа могут изображаться кругами, овалами, точками, прямоугольниками и т. д. Ненаправленная (без стрелки) линия, соединяющая вершины графа, называется ребром. Линия направленная (со стрелкой) называется дугой; при этом вершина, из которой дуга исходит, называется начальной, а вершина, куда дуга входит, — конечной.
Граф называется неориентированным, если его вершины соединены рёбрами (рис. 1.6, а). Вершины ориентированного графа соединены дугами (рис. 1.6, б). Путь — это последовательность рёбер (дуг), по которым можно перейти из одной вершины в другую.
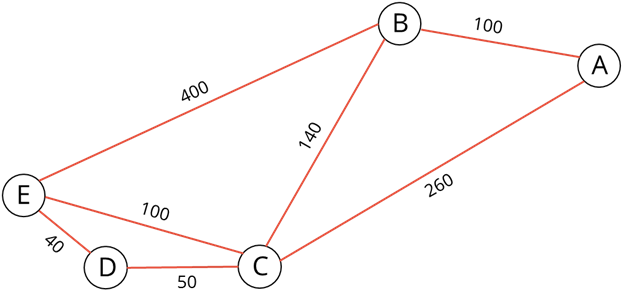
Граф называется взвешенным, если его вершины или рёбра характеризуются некоторой дополнительной информацией — весами вершин или рёбер. На рис. 1.6, в с помощью взвешенного неориентированного графа изображены дороги между пятью населёнными пунктами А, В, С, D, Е; веса рёбер — протяжённость дорог в километрах.
Путь по вершинам и рёбрам графа, в который любое ребро графа входит не более одного раза, называется цепью. Цепь, начальная и конечная вершины которой совпадают, называется циклом.
Рис. 1.6. Графы
Граф с циклом называется сетью. Если героев некоторого литературного произведения представить вершинами графа, а существующие между ними связи изобразить рёбрами, то мы получим граф, называемый семантической сетью.
Графы как информационные модели находят широкое применение во многих сферах нашей жизни. Например, можно существующие или вновь проектируемые дома, сооружения, кварталы изображать вершинами, а соединяющие их дороги, инженерные сети, линии электропередач и т. п. — рёбрами графа. По таким графам можно планировать оптимальные транспортные маршруты, кратчайшие объездные пути, расположение торговых точек и других объектов.
Дерево — это граф, в котором нет циклов, т. е. в нём нельзя из некоторой вершины пройти по нескольким различным рёбрам и вернуться в ту же вершину. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь.
Всякая иерархическая система может быть представлена с помощью дерева. У дерева выделяется одна главная вершина, называемая его корнем. Каждая вершина дерева (кроме корня) имеет только одного предка, обозначенный предком объект входит в один класс1* высшего уровня. Любая вершина дерева может порождать несколько потомков — вершин, соответствующих классам нижнего уровня. Такой принцип связи называется «один-ко-многим». Вершины, не имеющие порождённых вершин, называются листьями.
Родственные связи между членами семьи удобно изображать с помощью графа, называемого генеалогическим или родословным деревом.
Ресурс «Живая Родословная» (145555) — инструмент для формирования и анализа генеалогических деревьев, содержащий примеры родословных. С его помощью вы можете изучить генеалогические деревья многих известных семей и построить генеалогическое дерево своей семьи (http://sc.edu.ru/).
Класс — множество объектов, обладающих общими признаками.
1.3.3. Использование графов при решении задач
Графы удобно использовать при решении некоторых классов задач.
Пример 1. На рисунке 1.7 изображена схема дорог, связывающих торговые точки А, В, С, D, Е. По каждой дороге можно двигаться только в направлении, указанном стрелкой. Сколько существует различных путей от точки А до точки Е?
Рис. 1.7. Схема дорог, представленная ориентированным графом
В вершину Е можно попасть только из вершин С и D. Если мы будем знать число путей из вершины А в вершину С и из вершины А в вершину D, то, сложив их, получим искомое число путей из А в Е. Действительно, для того чтобы попасть из вершины А в вершину Е, мы просто все пути из вершины А в вершину С дополним дугой СЕ, а пути из вершины А в вершину D дополним дугой DE. Число путей при этом не изменится. Итак, число путей из вершины А в вершину Е равно сумме путей из А в С и из А в П.
Можно сказать, что наша задача распалась на две более простые задачи. Решим каждую из них в отдельности.
В вершину С можно попасть непосредственно из вершины А и из вершины В. В свою очередь, существует единственный путь из вершины А в вершину В. Таким образом, из вершины А в вершину С можно попасть двумя путями: 1 (напрямую из А) + 1 (через В) = 2.
Попробуйте доказать, что путь из вершины А в вершину В — единственный.
Что касается вершины D, она является конечной вершиной для трёх дуг: BD, AD и CD. Следовательно, в неё можно попасть из вершин А, В и С:
1 (напрямую из А) + 1 (через В) + 2 (через С) = 4.
Итак, существуют четыре пути из вершины А в вершину D.
Теперь выполним подсчёт путей из А в Е:
2 (через С) + 4 (через D) = 6.
Решение задачи будет гораздо проще, если двигаться от вершины А (начало маршрута) к вершине Е и проставлять веса вершин — число путей из А в текущую вершину (рис. 1.8). При этом вес вершины А можно принять за 1. Действительно, существует единственный способ попасть из А в А — оставаться на месте.
Рис. 1.8. Схема дорог, представленная взвешенным ориентированным графом
Пример 2. Для того чтобы записать все трёхзначные числа, состоящие из цифр 1 и 2, можно воспользоваться графом (деревом) на рис. 1.9.
Дерево можно не строить, если не требуется выписывать все возможные варианты, а нужно просто указать их количество. В этом случае рассуждать нужно так: в разряде сотен может быть любая из цифр 1 и 2, в разряде десятков — те же два варианта, в разряде единиц — те же два варианта. Следовательно, число различных вариантов: 2 • 2 • 2 = 8.
Рис. 1.9. Дерево для решения задачи о записи трёхзначных чисел
В общем случае, если известно количество возможных вариантов выбора на каждом шаге построения графа, то для вычисления общего количества вариантов нужно все эти числа перемножить. (Вспомните правило умножения из комбинаторики!)
Пример 3. Рассмотрим несколько видоизменённую классическую задачу о переправе.
На берегу реки стоит крестьянин (К) с лодкой, а рядом с ним — собака (С), лиса (Л) и гусь (Г). Крестьянин должен переправиться сам и перевезти собаку, лису и гуся на другой берег. Однако в лодку кроме крестьянина помещается либо только собака, либо только лиса, либо только гусь. Оставлять же собаку с лисой или лису с гусём без присмотра крестьянина нельзя — собака представляет опасность для лисы, а лиса — для гуся. Как крестьянин должен организовать переправу?
Для решения этой задачи составим граф, вершинами которого будут исходное и результирующее размещение персонажей на берегах реки, а также всевозможные промежуточные состояния, достигаемые из предыдущих за один шаг переправы. Каждую вершину-состояние переправы обозначим овалом и свяжем рёбрами с состояниями, образованными из неё (рис. 1.10).
Недопустимые по условию задачи состояния выделены пунктирной линией; они исключаются из дальнейшего рассмотрения. Начальное и конечное состояния переправы выделены жирной линией.
На графе видно, что существуют два решения этой задачи. Приведём соответствующий одному из них план переправы:
1) крестьянин перевозит лису;
2) крестьянин возвращается;
3) крестьянин перевозит собаку;
4) крестьянин возвращается с лисой;
5) крестьянин перевозит гуся;
6) крестьянин возвращается;
7) крестьянин перевозит лису.
Пример 4. Рассмотрим следующую игру: сначала в кучке лежат 5 спичек; два игрока убирают спички по очереди, причём за 1 ход можно убрать 1 или 2 спички; выигрывает тот, кто оставит в кучке 1 спичку. Выясним, кто выигрывает при правильной игре — первый (I) или второй (II) игрок.
Игрок I может убрать одну спичку (в этом случае их останется 4) или сразу 2 (в этом случае их останется 3).
Если после игрока II осталось 3 или 2 спички, то игрок I в каждой из этих ситуаций имеет шанс на выигрыш.
Таким образом, при правильной стратегии игры всегда выиграет первый игрок. Для этого своим первым ходом он должен взять одну спичку.
На рис. 1.11 представлен граф, называемый деревом игры; на нём отражены все возможные варианты, в том числе ошибочные (проигрышные) ходы игроков.
Рис. 1.11. Дерево игры
САМОЕ ГЛАВНОЕ
В графических информационных моделях для наглядного отображения объектов используются условные графические изображения (образные элементы), зачастую дополняемые числами, символами и текстами (знаковыми элементами). Примерами графических моделей могут служить всевозможные схемы, карты, чертежи, графики и диаграммы, графы.
Граф состоит из вершин, связанных линиями — рёбрами или дугами. Граф называется взвешенным, если его вершины или рёбра (дуги) характеризуются некоторой дополнительной информацией — весами вершин (рёбер, дуг).
Граф иерархической системы называется деревом. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь.
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?
Графические информационные модели. Графы
Урок 6. Информатика 9 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Графические информационные модели. Графы»
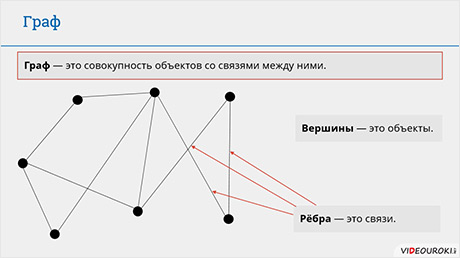
Граф – это совокупность объектов со связями между ними. Графически это будет выглядеть следующим образом:
Вершины (точки) – это объекты, а ребра (линии между ними) – это связи. Помимо точек вершины графа могут изображаться овалами, кругами, прямоугольниками и так далее. Связи между вершинами могут быть различными: дуги, рёбра, петли.
На данном уроке мы с вами познакомимся с ориентированными и неориентированными графами. В ориентированном графе связями между вершинами будут дуги, а в неориентированном – рёбра.
Решим задачу: В соревнованиях по шахматам участвовало 6 учащихся с 9 по 11 класс. При встрече они все обменялись рукопожатиями. Вопрос: сколько всего было сделано рукопожатий?
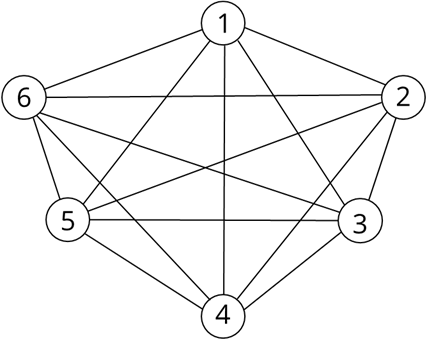
Для решения данной задачи будем использовать граф. Вершинами графов будут являться шесть учащихся, которые участвовали в турнире. Пронумеруем их от одного до шести. Проведем от каждой вершины линии (ребра) к оставшимся пяти вершинам.
Для ответа на вопрос остается сосчитать, сколько линий изображено на графе. Ответ: на турнире было сделано 15 рукопожатий.
Взвешенный граф – это граф, в котором вершины или рёбра характеризуются некоторой дополнительной информацией – весами вершин или рёбер.
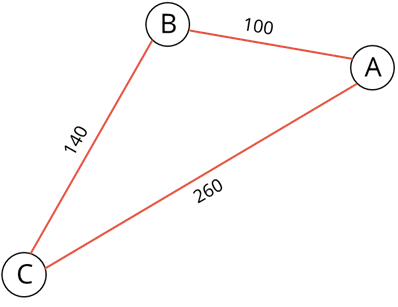
Давайте сами нарисуем взвешенный граф на основе задачи со следующим условием: Между городами A, B, C, D, Е построены дороги. Необходимо найти кратчайший путь из города А в город Е, если известно, что из города А в город В расстояние 100 километров, из А в С – 260 километров, из В в С – 140 километров, из В в Е – 400 километров, из С в D – 50 километров, из С в Е – 100 километров и из D в Е – 40 километров.
Итак, для решения данной задачи необходимо нарисовать взвешенный граф, так как нам дано расстояние, то есть вес рёбер. Для начала нарисуем вершину А. Из неё будут выходить два ребра в вершины В и С. Ребро из А в В будет короче, чем из А в С, так как расстояние из пункта А в пункт В 100 километров, а из пункта А в пункт С – 260 километров.
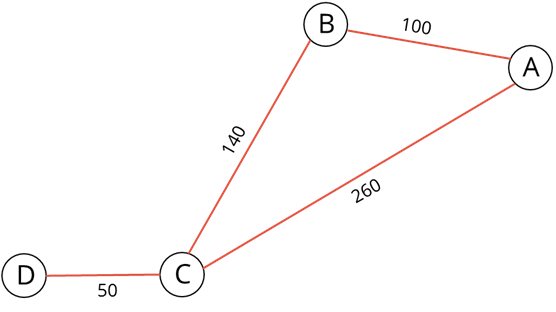
Далее нарисуем ребро из В в С и его вес будет равен 140.
Теперь нарисуем ребро из вершины С в вершину D и укажем вес 50
У нас получился взвешенный граф.
Нам осталось найти кратчайший путь. Для этого из вершины А будем идти в вершину В – это 100 километров, затем сразу в вершину Е. Слаживаем 100 и 400, получим 500 километров.
В свою очередь, цикл – это цепь, в которой начальная и конечная вершины совпадают. В детстве, наверное, каждый из вас рисовал звезду, не отрывая ручки от бумаги и не проходя дважды по одной и той же линии или ребру. При изображении такой звезды начальная и конечная вершины совпадают. Сеть – это граф с циклом.
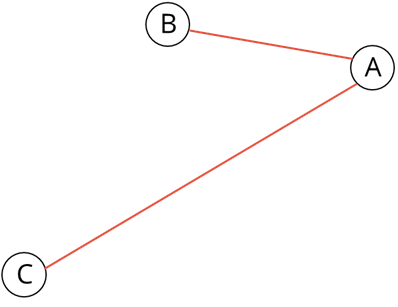
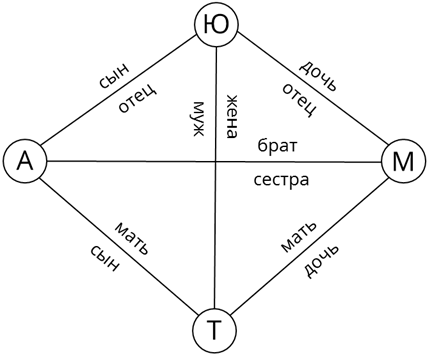
Разберём ещё один пример. У Антона в семье есть мама Татьяна, папа Юрий и сестра Маша. Изобразим каждого члена семьи как вершину нашего графа и обозначим первыми буквами имён. От каждого из них проведём рёбра к оставшимся троим. Над каждым из рёбер укажем, кто кем и кому приходится. Например, если идти от вершины Антона к Юрию, то Антон является сыном. А если идти наоборот, от Юрия к Антону, то Юрий является отцом. Аналогичным образом можно провести отношения между всеми членами семьи. Данный граф является примером семантической, или же смысловой сети.
Таким образом, Семантическая сеть – это информационная модель, имеющая вид графа, вершинам которого соответствуют определённые объекты, а рёбра задают отношения между ними. Все связи данного графа различны, поэтому их необходимо подписывать.
Графы широко распространены как информационные модели. Их можно применять, например, при планировании жилого района, где вершинами будут являться дома, а рёбрами – дороги или дорожки, которые их связывают. Ещё одним примером будет являться карта проезда по городу на любом из видов транспорта, где остановки – это вершины, а путь движения транспорта – это рёбра и так далее.
Следующее определение в данной теме: дерево. Дерево – это граф, в котором нет циклов, то есть в нём нельзя из некоторой вершины пройти по различным рёбрам и вернуться в ту же вершину. Отличительная особенность дерева: между любыми двумя его вершинами существует единственный путь. Корень дерева – это одна и единственная главная его вершина.
Каждая вершина дерева (кроме корня) имеет только одного предка. Обозначенный предком объект входит в один класс высшего уровня. Любая вершина дерева может порождать несколько потомков. Потомки – это вершины, которые соответствуют классам нижнего уровня. Такой принцип связи называется «один-ко-многим». Листья – это вершины, которые не имеют потомков.
Разберёмся более подробно на примере:
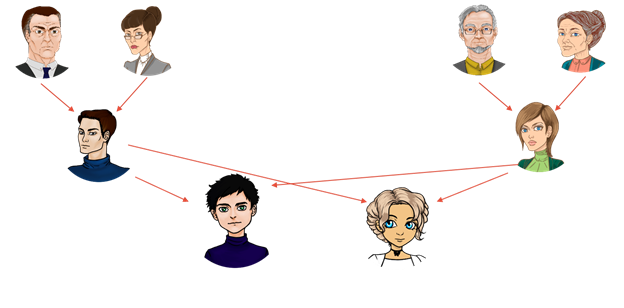
Ученик Антон решил составить генеалогическое дерево своей семьи. Для этого ему необходимо было узнать, кто в каких отношениях находится. То есть он является сыном своего отца Юрия и мамы Татьяны. В свою очередь Татьяна является дочерью Леонида (дедушки Антона) и Елены (бабушки Антона). Юрий является сыном Григория (дедушки Антона) и Марии (бабушки Антона). У Антона есть сестра Маша. Так как словесное описание трудно для восприятия, давайте поможем Антону представить это все в виде дерева и построим генеалогическое дерево.
Видим, что самыми старшими являются дедушки и бабушки Антона, поэтому расположим их в самом верху. У Леонида и Елены есть дочь Татьяна, а у Григория и Марии сын Юрий. Значит, разместим их на втором уровне (если считать сверху) и укажем их отношения с родителями в виде стрелок. У Татьяны и Юрия есть сын Антон и дочь Маша. Разместим их аналогичным образом на нашей схеме.
Таким образом, мы построили родословное дерево.
· Граф – это совокупность объектов со связями между ними.
· Вершины – это объекты, а ребра – это связи.
· Взвешенный граф – это граф, в котором вершины или рёбра характеризуются некоторой дополнительной информацией – весами вершин или рёбер.
· Цепь – это путь по вершинам и рёбрам графа, в который любое ребро графа входит не более одного раза.
· Цикл – это цепь, в которой начальная и конечная вершины совпадают.
· Сеть – это граф с циклом.
· Семантическая сеть – это информационная модель, имеющая вид графа, вершинам которого соответствуют определённые объекты, а рёбра задают отношения между ними.
· Дерево – это граф, в котором нет циклов, то есть в нём нельзя из некоторой вершины пройти по различным рёбрам и вернуться в ту же вершину.
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Графы
Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень)
§17. Графы.
Что такое граф?
Ключевые слова:
Давайте подумаем, как можно наглядно представить такую информацию:
От пос. Васюки три дороги идут в Солнцево, Грибное и Ягодное. Между Солнцевом и Грибным и между Грибным и Ягодным также есть дороги. Кроме того, есть дорога, которая идет из Грибного в лес и возвращается обратно в Грибное.
Нарисуйте в тетради схему дорог по этому описанию.
Можно, например, нарисовать такую схему (рис. 3.17, а).
Рис. 3.17
В информатике для исследования таких схем используют графы.
Граф — это набор вершин (узлов) и связей между ними — рёбер.
Граф, соответствующий нашей схеме дорог, показан на рис. 3.17, б, для краткости населённые пункты обозначены латинскими буквами.
Матрица смежности графа
Для хранения информации об узлах и связях показанного выше графа можно использовать таблицу такого вида (рис. 3.18).
Рис. 3.18
Единица на пересечении строки А и столбца В означает, что между вершинами А и В есть связь. Ноль указывает на то, что связи нет. Такая таблица называется матрицей смежности. Она симметрична относительно главной диагонали (см. закрашенные клетки в таблице).
Исследуйте матрицу смежности и сравните её с графом на рис. 3.17, б. Что означает единица на пересечении столбца С и строки С?
В этом графе есть петля — ребро, которое начинается и заканчивается в одной и той же вершине.
Степенью вершины называют количество рёбер, с которыми связана вершина. При этом петля считается дважды (с вершиной связаны оба конца ребра!).
Подсчитайте по матрице смежности, сколько ребёр в графе. Определите степени всех вершин. Как вы рассуждали?
Строго говоря, граф — это математический объект, а не рисунок. Конечно, его можно нарисовать на плоскости (например, как на рис. 3.17, б), но матрица смежности не даёт никакой информации о том, как именно располагать вершины друг относительно друга. Для таблицы, приведённой выше, возможны, например, такие варианты (рис. 3.19).
Рис. 3.19
Нарисуйте по матрице смежности (рис. 3.20) два разных изображения графа.
Рис. 3.20
Граф имеет 4 вершины, причём каждая вершина связана рёбрами со всеми остальными. Нарисуйте этот граф. Сколько всего рёбер в этом графе?
Граф имеет N вершин, причём каждая вершина связана рёбрами со всеми остальными. Сколько всего рёбер в этом графе?
Граф имеет 4 ребра. Чему равна сумма степеней вершин в этом графе? Зависит ли она от количества вершин?
Граф имеет N рёбер. Чему равна сумма степеней вершин в этом графе?
Попробуйте нарисовать граф с пятью вершинами, где все вершины имеют степень 3. Получилось ли у вас? Почему?
Связный граф
В графе на рис. 3.17, б все вершины связаны: между любой парой вершин существует путь — последовательность вершин, в которой каждая следующая связана ребром с предыдущей. Такой граф называется связным.
Связный граф — это граф, между любыми вершинами которого существует путь.
Теперь представьте себе, что дороги Васюки-Солнцево, Васю- ки-Грибное и Грибное-Ягодное завалило снегом (или размыло дождём) так, что по ним ни пройти, ни проехать (рис. 3.21).
Рис. 3.21
Эту схему тоже можно считать графом (она соответствует определению), но в таком графе есть две несвязанные части, каждая из которых — связный граф. Такие части называют компонентами связности.
Постройте матрицу смежности графа, изображённого на рис. 3.21.
Граф имеет 4 вершины и две компоненты связности. Какое наибольшее количество рёбер может быть в этом графе, если в нём нет петель? Нарисуйте этот граф.
Вспоминая материал предыдущего параграфа, можно сделать вывод, что дерево — это частный случай связного графа. Но у него есть одно важное свойство — в дереве нет замкнутых путей — циклов, т. е. путей, которые начинаются и заканчиваются в одной и той же вершине.
Найдите все циклы в графе на рис. 3.17.
Дерево — это связный граф, в котором нет циклов.
Взвешенный граф
Если в нашем примере нас заинтересует не только наличие дорог между посёлками, но ещё и расстояния между ними, каждой связи нужно сопоставить число — вес ребра (рис. 3.22).
Рис. 3.22
Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра.
Весом может быть не только расстояние, но и, например, стоимость проезда или другая величина.
Рис. 3.23
Так же как и матрица смежности, весовая матрица симметрична относительно диагонали.
Что означают пустые ячейки в весовой матрице?
Как по весовой матрице сразу определить, сколько рёбер в графе?
Определите по весовой матрице (рис. 3.24) длины путей ADBEC, ABDCE, DEBAC. Как вы рассуждали?
Рис. 3.24
Оптимальный путь в графе
Для того чтобы определить оптимальный (наилучший) путь между двумя вершинами графа, нужно ввести какой-то числовой показатель, по которому можно сравнивать пути — определять, какой из них лучше. Обычно для оценки пути используют сумму весов ребёр, входящих в этот путь. Например, при поиске кратчайшего пути чем меньше это значение, тем лучше.
Какие показатели вы используете в жизни для определения оптимального пути? Всегда ли самый короткий путь — самый лучший?
Если в графе немного узлов, по весовой матрице можно легко определить оптимальный путь из одной вершины в другую простым перебором вариантов. Рассмотрим граф, заданный весовой матрицей на рис. 3.25 (числа определяют стоимость поездки между соседними пунктами).
Рис. 3.25
Найдём наилучший путь из А в В — такой, при котором общая стоимость поездки минимальная.
Для решения задачи будем строить дерево перебора вариантов. Видим, что из пункта А напрямую
Рис. 3.26
Числа около рёбер обозначают стоимость поездки по этому участку, а индексы у названий узлов показывают общую стоимость проезда в данный узел из узла А. Теперь разберём варианты дальнейшего движения из узла С I tM lt;pb р (рис. 3.27).
Рис. 3.27
Почему, на ваш взгляд, на схеме не показана возможность движения из С в А?
Видим, что из С сразу можно попасть в В, стоимость проезда в этом случае равна 7.
Почему нельзя на этом остановиться, ведь путь из А в В найден?
Проверяя пути через узел В, выясняем, что можно сократить стоимость до 6 (рис. 3.28)
Рис. 3.28
Нужно ли исследовать дальше путь, содержащий цепочку ACED? Сравните стоимость этого пути и стоимость уже найденного пути из А в В.
Аналогично строим вторую часть схемы (рис. 3.29).
Рис. 3.29
Таким образом, оптимальный (наилучший) путь — ADEB, его стоимость — 3.
Нужно ли проверять пути ACED и ADEC, не дошедшие до узла В? Могут ли они улучшить результат?
Конечно, для более сложных графов метод перебора работает очень долго, поэтому используются более совершенные (но значительно более сложные) методы.
Ориентированный граф
Наверное, вы заметили, что при изображении деревьев, которые описывают иерархию (подчинение), мы ставили стрелки от верхних уровней к нижним. Это означает, что для каждого ребра указывается направление, и двигаться можно только по стрелкам, но не наоборот.
Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление.
Орграф может служить, например, моделью системы дорог с односторонним движением. Матрица смежности и весовая матрица для орграфа уже не обязательно будут симметричными.
На схеме на рис. 3.30 всего две дороги с двусторонним движением, по остальным можно ехать только в одну сторону.
Рис. 3.30
Рёбра в орграфе называют дугами. Дуга, в отличие от ребра, имеет начало и конец.
Нарисуйте граф по весовой матрице, показанной на рис. 3.31. С помощью дерева перебора найдите все возможные пути из вершины А в вершину Е, не проходящие дважды через одну и ту же вершину, и стоимости проезда по каждому из этих путей. Определите оптимальный путь из вершины А в вершину Е.
Рис. 3.31
Количество путей
Определим количество возможных путей из вершины А в вершину К для ориентированного графа, показанного на рис. 3.32.
Рис. 3.32
Так как граф ориентированный, переходить в другую вершину можно только по стрелкам.
В графе на рис. 3.32 есть одна начальная вершина А, из которой дуги только выходят. Такая вершина называется истоком. Вершина, в которую дуги только входят (и ни одна не выходит), называется конечной вершиной или стоком. В нашем графе сток — это вершина К.
По весовой матрице на рис. 3.31 найдите исток и сток в графе. Как вы рассуждали?
Будем двигаться по стрелкам от начальной вершины А. Около каждой вершины запишем количество возможных путей из вершины А в эту вершину. В вершину А существует единственный путь — пустой (никуда не ехать). Найдём все вершины, в которые можно приехать только из А: это вершины Б и Г, записываем около них количество путей 1 (рис. 3.33).
Рис. 3.33
Теперь ищем вершины, в которые можно попасть только из уже отмеченных вершин. Например, в вершину В есть один путь из А напрямую, а также по одному пути через Б и Г (так как эти вершины отмечены числом 1). Общее количество путей из А в Б равно сумме отметок предыдущих вершин: для вершины В получаем 3 пути. В вершину Ж можно попасть только из Г, поэтому число путей в Г и Ж совпадает (рис. 3.34).
Рис. 3.34
В вершину Д идёт один путь через Б и три пути через В, поэтому общее число путей — 4. Аналогично получаем 4 пути в вершину Е: 3 пути через В и один через Ж (рис. 3.35).
Рис. 3.35
Далее находим один путь из А в И (только через Ж) и 4 пути из А в 3 (все через Д). В конечную вершину К можно приехать через вершины Д (4 пути), 3 (4 пути), Е (4 пути) и И (1 путь), таким образом, общее количество различных путей равно 13 (рис. 3.36).
Рис. 3.36
Выводы
• Граф — это набор вершин (узлов) и связей между ними — рёбер.
• Матрица смежности — это таблица, в которой единица на пересечении строки и столбца обозначает ребро между соответствующими вершинами, а ноль — отсутствие ребра.
• Связный граф — это граф, между любыми вершинами которого существует путь.
• Цикл — это замкнутый путь в графе.
• Дерево — это связный граф, в котором нет циклов.
• Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра. Взвешенный граф описывается весовой матрицей.
• Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление. Рёбра орграфа называют дугами. Матрица смежности и весовая матрица орграфа могут быть несимметричными.
Нарисуйте в тетради интеллект-карту этого параграфа.
Вопросы и задания
1. Можно ли сказать, что лес (множество деревьев) — это граф? Почему?
2. Как по матрице смежности определить, есть ли петли в графе?
3. Как по весовой матрице определить длину пути в графе?
4. Когда для представления данных используются орграфы? Приведите примеры.
5. Выполните по указанию учителя задания в рабочей тетради.
Подготовьте сообщение
а) «Задача о Кёнигсбергских мостах»
б) «Решение логических задач с помощью графов»