Что такое вертикальная плоскость
Вертикальная плоскость
Плоскости частного положения
В зависимости от расположения относительно плоскостей проекций различают плоскости частного положения и плоскости общего вида. Под «частным» понимают такое расположение плоскостей, когда они параллельны или перпендикулярны плоскостям проекций.
Плоскости, параллельные плоскостям проекций называются плоскостями уровня.
Плоскости перпендикулярные плоскостям проекций, и поэтому проецирующиеся на них в виде прямой линии, называют проецирующими плоскостями.
Фронтальная плоскость Ф
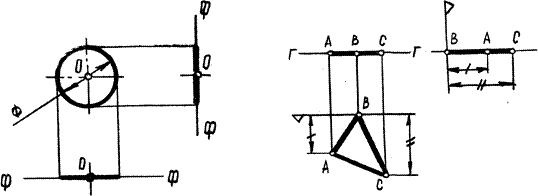 |
Это плоскость параллельная фронтальной плоскости проекций(рисунок 3-1).
Рисунок 3-1 Рисунок 3-2
Горизонтальная плоскость Г
Это плоскость параллельная горизонтальной плоскости проекций.
Всякая плоская фигура, лежащая в этой плоскости, на виде сверху изображается в натуральную величину (рисунок 3-2), а на видах спереди и слева – как отрезки прямой совпадающие с проекциями самой горизонтальной плоскости.
Профильная плоскость П
Вертикальная плоскость
Дата добавления: 2015-11-06 ; просмотров: 1114 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Вертикальная плоскость
46. Вертикальная плоскость
Плоскость, проходящая через отвесную линию данной точки
Смотри также родственные термины:
5.2. Вертикальная плоскость 2: проходит через главную продольную ось машины, то есть посредине между колесами (или гусеницами).
Полезное
Смотреть что такое «Вертикальная плоскость» в других словарях:
вертикальная плоскость — Плоскость, проходящая через отвесную линию данной точки. [ГОСТ 22268 76] Тематики геодезия Обобщающие термины системы координат EN vertical plane DE Vertikalebene FR plan vertical … Справочник технического переводчика
Вертикальная плоскость 2 — 5.2. Вертикальная плоскость 2: проходит через главную продольную ось машины, то есть посредине между колесами (или гусеницами). Источник: ГОСТ 27248 87: Машины землеройные. Метод определения положения центра тяжести … Словарь-справочник терминов нормативно-технической документации
ПЛОСКОСТЬ СТРЕЛЬБЫ — вертикальная плоскость, проведенная через ось канала орудия. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 Плоскость стрельбы вертикальная плоскость, проходящая через линию выстр … Морской словарь
плоскость отсчета системы МЛС — Вертикальная плоскость, проходящая через ось взлетно посадочной полосы или площадки для азимутальных радиомаяков системы МЛС, и горизонтальная плоскость, проходящая через фазовый центр антенны для угломестных радиомаяков системы МЛС. [ГОСТГОСТ… … Справочник технического переводчика
ПЛОСКОСТЬ БОМБОМЕТАНИЯ — вертикальная плоскость, проведенная через точку сбрасывания и расположенная в направлении путевой скорости самолета. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 … Морской словарь
ПЛОСКОСТЬ КОМПАСНОГО МЕРИДИАНА — вертикальная плоскость, проходящая через ось магнитной стрелки, находящейся под действием силы земного магнетизма и испытывающей на себе влияние магнитных сил судового железа. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское… … Морской словарь
ПЛОСКОСТЬ МАГНИТНОГО МЕРИДИАНА — вертикальная плоскость, проходящая через ось магнитной стрелки, находящейся под действием только силы земного магнетизма. Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 … Морской словарь
Плоскость мидель-шпангоута — 17. Плоскость мидель шпангоута По ГОСТ 1062 80 Источник: ГОСТ 13641 80: Элементы м … Словарь-справочник терминов нормативно-технической документации
Плоскость мидель-шпангоута плавучего дока — 5. Плоскость мидель шпангоута плавучего дока Плоскость мидель шпангоута Вертикальная плоскость, перпендикулярная диаметральной плоскости и пересекающая плавучий док посередине его длины по стапель палубе Источник: ГОСТ 14181 78: Доки плавучие.… … Словарь-справочник терминов нормативно-технической документации
Вертикальная плоскость
Плоскости частного положения
В зависимости от расположения относительно плоскостей проекций различают плоскости частного положения и плоскости общего вида. Под «частным» понимают такое расположение плоскостей, когда они параллельны или перпендикулярны плоскостям проекций.
Плоскости, параллельные плоскостям проекций называются плоскостями уровня.
Плоскости перпендикулярные плоскостям проекций, и поэтому проецирующиеся на них в виде прямой линии, называют проецирующими плоскостями.
Фронтальная плоскость Ф
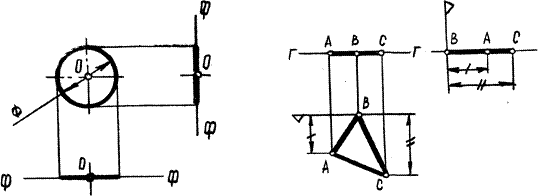 |
Это плоскость параллельная фронтальной плоскости проекций(рисунок 3-1).
Рисунок 3-1 Рисунок 3-2
Горизонтальная плоскость Г
Это плоскость параллельная горизонтальной плоскости проекций.
Всякая плоская фигура, лежащая в этой плоскости, на виде сверху изображается в натуральную величину (рисунок 3-2), а на видах спереди и слева – как отрезки прямой совпадающие с проекциями самой горизонтальной плоскости.
Профильная плоскость П
Вертикальная плоскость
Дата добавления: 2017-11-21 ; просмотров: 3516 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Вертикальная плоскость
Вертикальная плоскость — это плоскость, которая параллельна вертикали.
В практической деятельности вертикальность или горизонтальность определяется при помощи таких приборов как теодолит, отвес, уровень, угломер.
Содержание
История
Исторически понятия вертикали и горизонтали, а также соответствующие им плоскости возникли в процессе геометризации и координатизации человеком окружающей его земной поверхности. [6]
Отвес известен человечеству с незапамятных времён и представляет из себя приспособление, состоящее из тонкой нити и грузика на её конце, позволяющее судить о правильном вертикальном положении и служащее для вертикальной юстировки. Под действием силы тяжести нить принимает постоянное направление (отвесная линия).
Египтяне изобрели инструмент, напоминающий букву E, от которого отвесная линия была подвешена к верхней внешней части E. Проверка на вертикальность поверхности достигается путём прикладывания к ней отвеса. Положение поверхности вертикально, если нить прикасается к нижнему выступу отвеса, оставаясь при этом ровной. Как ни странно, этот полезный инструмент, по-видимому, был забыт на многие века и вновь появился только в наше время. [8]
В эллинистический период совокупность знаний о землемерии разделилась на геометрию и геодезию, которые впоследствии дали жизнь многообразным прикладным и теоретическим наукам, которые существуют в современности. [6]
Обобщения без учёта силы тяжести
Вертикаль и горизонталь а также соответствующие им плоскости в качестве базовых понятий начертательной геометрии и в инженерной графике могут описывать объекты, находящиеся вне действия силы тяжести (например, на МКС. где сила тяжести компенсирована центробежной силой), [9] либо объекты, которые в процессе эксплуатации меняют свою ориентацию относительно горизонтали и вертикали (элемненты водных судов, автотранспорта и т. п.)
В математике
Написание курсовой работы «под ключ»
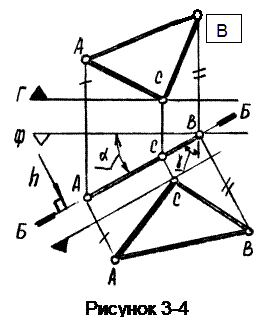
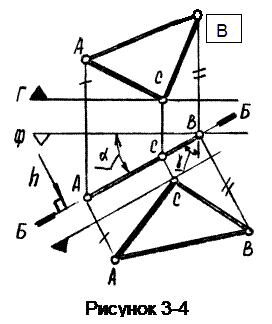
Эта плоскость перпендикулярна горизонтальной плоскости уровня (рисунок 3-4).
6.5 Наклонная плоскость
Это плоскость перпендикулярная фронтальной плоскости. Д ^ Ф (рисунок 3-5). Название плоскости определяется ее положением относительно горизонтальной плоскости.
На виде спереди плоскость изображается как прямая, а на виде сверху занимает всю плоскость проекций.
Изображение любой плоской фигуры лежащей в плоскости Д (например D АВС) на виде спереди совпадает с изображением плоскости, а на виде сверху размеры и форма фигуры изображаются с искажением.
6.6 Плоскость перпендикулярная профильной плоскости проекций
Эта плоскость на виде слева изображается в виде прямой, а на виде спереди занимает всю плоскость проекций. Б ^ П (рисунок 3-6).
Фигура, лежащая в плоскости Б на виде слева совпадает с изображением плоскости, а на виде спереди изображается с искажением размеров и формы.
Для определения натуральной величины фигуры строим дополнительный вид на плоскость параллельную заданной плоскости Б (или по направлению профильной прямой р перпендикулярной заданной плоскости Б ).
Плоскости общего положения
Плоскостью общего положения называют плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.
В общем случае ее изображение занимает все поле чертежа. Чтобы сделать чертеж более удобным и наглядным, плоскость общего положения ограничивают, задавая ее одним из следующих способов:
1. Тремя точками, не лежащими на одной прямой – Б(А, В, С);
2. Двумя параллельными прямыми – Д(а // b);
3. Двумя пересекающимися прямыми –Ж(c Ç f/;
4. Точкой и прямой – 3 (М, м);
При этом всегда можно перейти от одного способа задания плоскости к другому.
Если плоскость по мере удаления от наблюдателя поднимается вверх, то такую плоскость называют восходящей.
И наоборот, если плоскость по мере удаления от наблюдателя понижается, то такую плоскость называют нисходящей.
На комплексном чертеже оба вида треугольника, которым задана восходящая плоскость, имеют одинаковые обходы (рис. 3-7а). Изображения треугольника, задающего нисходящую плоскость, имеют противоположные обходы (рисунок 3-7б).
ВЗАИМОПРИНАДлЕЖНОСТЬ ТОЧКИ, ПРЯМОЙ И ПЛОСКОСТИ
8.1 Взаимное положение точки и прямой
Относительно прямой общего положения l (рисунок 3-8) построим следующие точки:
1. точка А принадлежит l (А Î l). Задача решается на основании свойства принадлежности;
2. точка В над прямой.
Как построить точку на прямой мы теперь знаем, а поскольку она должна быть над прямой, т, е. выше нее, необходимо внести соответствующее изменение в положение точки на виде спереди;
3. точка С за прямой.
Аналогично предыдущей задаче приходим к выводу, что за прямой означает дальше нее, чему соответствует изменение положения точки на виде сверху.
8.2 Точка и плоскость, прямая и плоскость
Дана плоскость общего положения Б ( D АВС), (рисунок 3-9).
Построим точку М на плоскости Б и точку N под плоскостью Б.
Чтобы построить точку на плоскости, необходимо:
1) на этой плоскости Б провести (или выделить) любую прямую l, для чего провести прямую l через две точки принадлежащие плоскости (в нашем случае т.т. А и 1);
2) на этой прямой взять произвольную точку, например М (свойство принадлежности).
Чтобы построить точку N под заданной плоскостью, необходимо вначале, как сказано выше, найти точку, принадлежащую плоскости, а затем, на, виде спереди изображение ее опустить ниже прямой l (значит и ниже плоскости).

