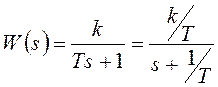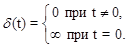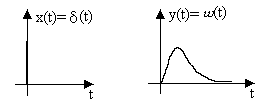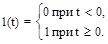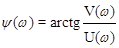Что такое весовая характеристика звена

В наиболее сложных случаях для нахождения оригинала по изображению используют теоремы разложения.

Получение переходной функции интегрированием весовой характеристики.

Такая возможность является следствием (6.1) и свойств весовой характеристики, которые будут рассмотрены ниже.

Получение переходной функции на основе анализа преобразования звеном входного сигнала.

Данный способ удобен в ряде частных случаев и основан на представлении звена или системы в виде последовательной или параллельной цепи из простейших звеньев. Например, изодромное звено с передаточной функцией 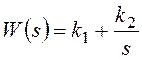может быть представлено параллельным соединением безынерционного и идеального интегрирующего звеньев (рисунок 44).

Первое звено масштабирует входной сигнал, второе интегрирует. Результирующая передаточная функция получается суммированием выходных сигналов этих звеньев:

.

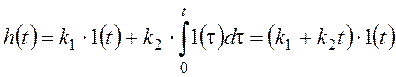
Обсудим свойства звена или системы, которые отражает и позволяет анализировать переходная характеристика, на примере апериодического звена 1-го порядка. Полученная для него переходная характеристика (рисунок 41) показывает, что апериодическое звено 1-го порядка воспроизводит входной сигнал. Но это происходит с замедлением – по окончании переходного процесса. То есть данное звено характеризуется инерционностью.

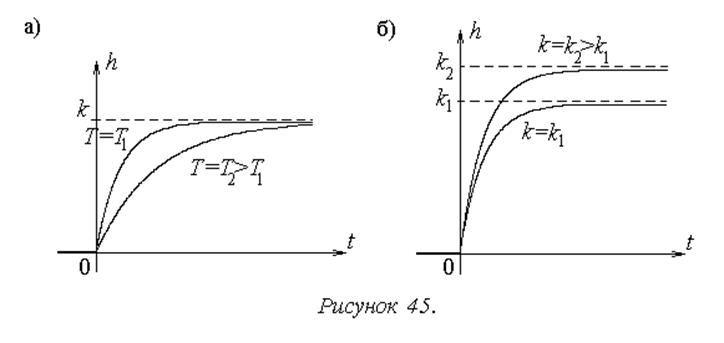
На рисунке 45а показаны варианты этой же переходной характеристики для двух различных значений постоянной времени.

Таким образом, при увеличении значения постоянной времени переходный процесс замедляется. Постоянная времени характеризует инерционность динамического звена.

На рисунке 45б отображено влияние на процесс в звене коэффициента передачи.

Теперь проведем краткий анализ динамических свойств типовых звеньев, отражаемых переходной характеристикой.

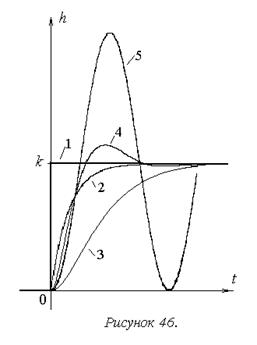
На рисунке 46 показаны переходные характеристики типовых позиционных звеньев.

На основе их сравнительного анализа можно сделать следующие выводы:

1. Общим свойством звеньев данной группы является пропорциональность выходного сигнала входному, обеспечиваемая по окончании переходного процесса. Именно это свойство является единственным для идеального звена данной группы – безынерционного (1).

2. Общее отличие всех звеньев от безынерционного состоит в наличии переходного процесса, вызванном их инерционностью. Различия же между звеньями внутри группы определяются количеством и соотношением постоянных времени, то есть характером инерционности.

Так процесс в звеньях второго порядка – апериодическом 2-го порядка (3), колебательном (4) и консервативном(5) – в отличие от апериодического звена 1-го порядка (2), начинает развиваться не мгновенно, так как здесь и начальная скорость изменения сигнала – нулевая.

Кроме того, в зависимости от соотношения постоянных времени у звеньев второго порядка наблюдается различный характер процесса.

Динамические свойства, отражаемые переходной характеристикой, определили названия типовых динамических звеньев.

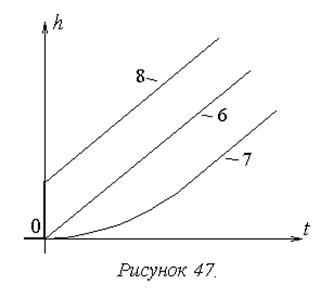
На рисунке 47 показаны переходные характеристики типовых интегрирующих звеньев.

На основе их сравнительного анализа можно сделать следующие выводы:

1. Общее свойство звеньев данной группы отражается характеристикой идеального интегрирующего звена (6) – в установившемся процессе выходной сигнал пропорционален интегралу входного.

2. У остальных звеньев данной группы проявляются дополнительные динамически свойства: инерционность у интегрирующего звена с замедлением (7) и противоположный эффект у изодромного звена (8), приводящий к тому, что процесс в данном звене ускоряется по сравнению с процессом в идеальном звене. Формально такая разница в динамических свойствах отражается расположением постоянной времени в передаточной функции: в знаменателе при наличии инерционности и в числителе в противоположном случае.

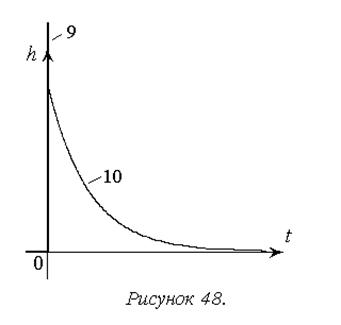
На рисунке 48 показаны переходные характеристики типовых дифференцирующих звеньев.

На основе их сравнительного анализа можно сделать следующие выводы:

1. Общее свойство звеньев данной группы отражается характеристикой идеального дифференцирующего звена (9) – в установившемся процессе выходной сигнал пропорционален производной входного.

2. Наличие инерционности у дифференцирующего звена с замедлением (10) приводит к переходному процессу.

Весовая характеристика (весовая функция, функция веса) – это реакция звена или системы на входной сигнал в виде d-функции (функции Дирака).

Вспомним основные свойства d-функции:

, , .

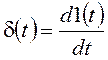
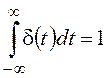
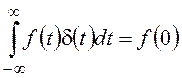
Рассмотрим наиболее удобные способы (методы) получения весовой характеристики.

Воспользуемся определениями передаточной функции и весовой характеристики с учетом известного изображения по Лапласу d-функции :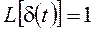

.

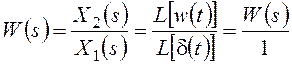
Следовательно, передаточная функция является изображением по Лапласу функции веса.

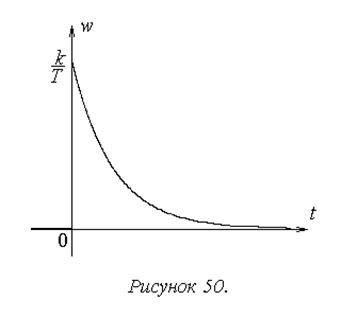
Найдем весовую характеристику апериодического звена 1-го порядка.

Преобразуем передаточную функцию звена к табличному виду

и запишем результат:

.

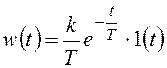
График весовой характеристики показан на рисунке 50.

Получение весовой функции дифференцированием переходной характеристики.

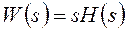
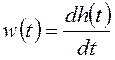
Следствием полученного выше соотношения является следующая связь между весовой и переходной функциями:

.

Вернемся к последнему примеру.

Переходная характеристика апериодического звена 1-го порядка была получена выше:

.

.

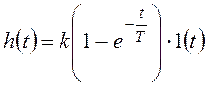
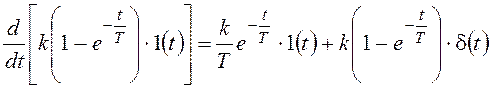
С учетом тождественного равенства нулю d-функции при всех 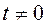упростим полученное выражение:

.

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Характеристики линейных звеньев

Под динамическим звеном понимается устройство любого физического вида и конструктивного оформления, но имеющее определенное математическое описание.

В качестве входных воздействий, на которые ищется реакция звена, приняты воздействия, описываемые элементарными математическими функциями, то есть такими, на которые можно разложить любые произвольные функции. В теории управления в качестве элементарных функций используются:

1) единичная импульсная или дельта-функция d(t);

2) единичная ступенчатая функция 1(t);

3) гармоническая функция X₀sin(wt).

Существуют временные (импульсная и переходная функции) и частотные характеристики.

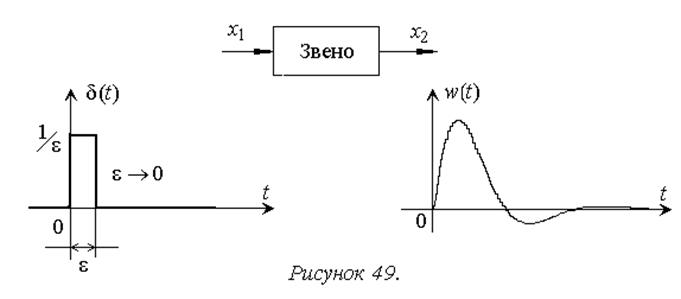
Импульсная или весовая функция звена w(t).Импульсная или весовая функция представляет собой реакцию звена на единичную импульсную функцию.

Единичной импульсной функцией или d-функцией называется функция, равная нулю всюду, кроме начала координат, но притом так, что интеграл от нее по любому интервалу, содержащему нуль, равен единице, т.е.

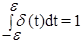
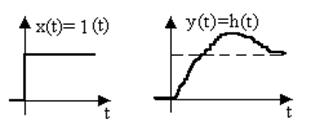
Кроме того, при любом e>0.

Рис. 3.1. Временные диаграммы входного и выходного сигналов звена

Иначе говоря, весовая функция w(t) представляет собой переходный процесс на выходе звена (рис. 3.1) при подаче на его вход единичного импульса.

Весовой функцией звена w(t) называется оригинал (т.е. обратное преобразование Лапласа) передаточной функции, а именно:

(3.1)

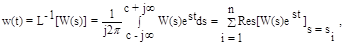
Зная импульсную функцию w(t), можно найти реакцию звена на любое входное воздействие x(t), разложение которого на d-функции имеет вид:

. (3.2)

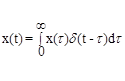
При этом сигнал на выходе линейного звена определяется как

, (3.3)

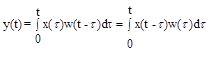
Имея весовую функцию звена w(t), можно определить его передаточную функцию:

. (3.4)

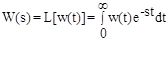
Переходная функция звена h(t).Переходная функция представляет собой реакцию звена на единичную ступенчатую функцию, удовлетворяющую условию

Как видим (рис. 3.2), переходная функция является переходным процессом на выходе звена при единичном скачке на его входе.

Рис. 3.2. Временные диаграммы входного и выходного сигналов звена

Из рассмотренного выше для линейных звеньев очевидны следующие соотношения между импульсной и переходной функциями. Поскольку

, то ,

, то .

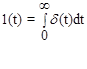
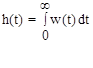
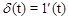
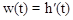
Переходная функция звена связана с передаточной функцией преобразованием Карсона, т.е. имеется следующее интегральное преобразование:

. (3.5)

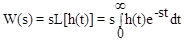
Весовая и переходная характеристики являются функциями времени и поэтому относятся к временным характеристикам.

Частотные характеристики звена.Частотными характеристиками называются формулы и графики, характеризующие реакцию звена на гармоническое входное воздействие в установившемся режиме, т.е. вынужденные синусоидальные колебания звена.

Если на вход линейного звена подать гармоническое воздействие

то, как следует из необходимых и достаточных условий линейности, на выходе звена в установившемся режиме будет также гармоническая функция той же частоты, но, в общем случае, другой амплитуды Y₀ и сдвинутая по фазе относительно входной величины на угол y

Связь между выходной гармоникой и входной устанавливается с помощью частотной передаточной функции звена W(jw).

Частотная передаточная функция является важнейшей динамической характеристикой звена и представляет собой отношение изображений по Фурье выходного и входного сигналов при нулевых начальных условиях и равных нулю воздействиях на остальных входах:

(3.6)

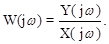
Из сравнения преобразований Фурье и Лапласа следует, что частотную передаточную функцию звена легко получить из его передаточной функции путем замены s на jw, т.е.

(3.7)

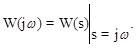
Частотная передаточная функция W(jw), как видно, представляет собой комплексное число, которое можно записать как в полярной, так и декартовой системах координат:

W(jw) = A(w) 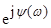= U(w) + jV(w), (3.8)

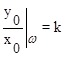
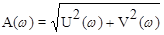
А(w) = | W(jw) | = mod W(jw) = ; (3.9)

и

связывают между собой составляющие частотной передаточной функции.

Таким образом, частотная передаточная функция, определяющая реакцию звена на гармонические колебания всех возможных частот, позволяет, пользуясь принципом суперпозиции, найти реакцию линейного звена на произвольное воздействие.

Для наглядного представления частотных свойств звена частотные характеристики отображают графически.

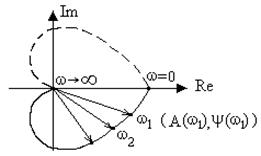
Амплитудно-фазовая частотная характеристика (АФЧХ).Строится на комплексной плоскости и представляет собой геометрическое место концов векторов (годографов), соответствующих частотной передаточной функции W(jw) при изменении частоты от нуля до бесконечности (рис.3.3). Для каждой частоты w на комплексной плоскости наносится точка, полученные точки соединяются затем плавной кривой. АФЧХ можно строить как в декартовых координатах (U, V), так и в полярных (A, y).

Рис. 3.3. Амплитудно-фазовая частотная характеристика

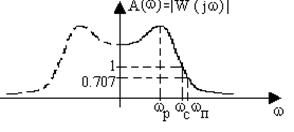
Амплитудная частотная характеристика (АЧХ).Показывает, как пропускает звено сигнал различной частоты, иначе, представляет собой коэффициент изменения амплитуды гармонических колебаний при прохождении через звено (рис. 3.4).

Рис. 3.4. Амплитудная частотная характеристика

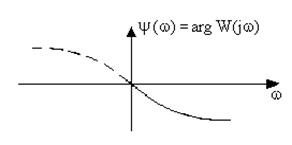
Фазовая частотная характеристика (ФЧХ).Показывает фазовые сдвиги, вносимые звеном на различных частотах (рис.3.5).

Рис. 3.5. Фазовая частотная характеристика

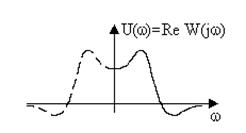
Вещественная частотная характеристика (ВЧХ).Представляет собой зависимость вещественной составляющей частотной передаточной функции от частоты (рис. 3.6).

Рис. 3.6. Вещественная частотная характеристика

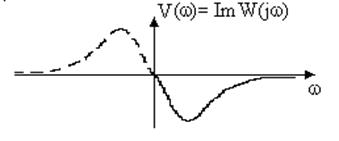
Мнимая частотная характеристика (МЧХ).Представляет собой зависимость мнимой составляющей частотной передаточной функции от частоты (рис.3.7).

Рис. 3.7. Мнимая частотная характеристика

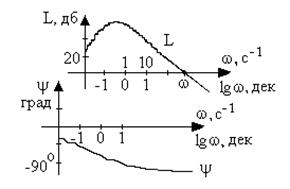
Логарифмические частотные характеристики (ЛЧХ).На практике чаще всего амплитудную и фазовую частотные характеристики изображают в логарифмическом масштабе (рис. 3.8).

Рис. 3.8. Логарифмические частотные характеристики

При построении логарифмической амплитудной частотной характеристики (ЛАХ) по оси ординат откладывают величину

L(w) = 20 lg A(w) = 20 lg|W(jw)|. (3.13)

Источник

Исследование весовых и переходных характеристик простейших типовых линейных звеньев

Работа № 2

Исследование весовых и переходных характеристик простейших типовых линейных звеньев

Продолжительность работы – 4 часа

2.1. Цель работы

Исследование особенностей реакций простейших типовых звеньев на импульсное воздействие, единичное ступенчатое и линейное воздействия.

2.2. Теоретическое обоснование

По определению, переходной характеристикой h(t) называется реакция системы на единичное ступенчатое 1(t) входное воздействие при нулевых начальных условиях

Преобразование Лапласа от единичной ступенчатой функции 1(t) получаем, подставляя эту функцию в интеграл Лапласа:

Переходная характеристика вычисляется по формуле:

.

Весовой, или импульсной функцией w(t) называют реакцию системы на единичный импульс (t). При анализе систем управления приходится часто использовать δ – функцию, которая обладает следующими свойствами:

Преобразование Лапласа от этой функции

К простейшим типовым элементарным звеньям относятся такие, знаменатель и числитель передаточной функции W(s) которых, имеют порядок не выше единицы, т. е.

— постоянные коэффициенты.

В теории автоматического управления [1] принята определенная классификация простейших типовых звеньев (элементарных) звеньев, которые рассматриваются ниже.

2.2.1. Пропорциональное звено

Пропорциональным называется звено, сигнал на выходе которого, y(t) пропорционален входному сигналу x(t):

К таким звеньям относятся зубчатые передачи редукторов, рычажные передачи, делители напряжений на резисторах, широкополосные усилители постоянного тока.

Подвергая уравнение (2.1) преобразованию Лапласа, имеем:

где K-передаточный коэффициент, или коэффициент усиления.

В связи с этим пропорциональные звенья также называют усилительными.

Пропорциональное звено имеет передаточную функцию

,

где — передаточный коэффициент или коэффициент усиления. Переходная функция пропорционального звена

На рис.2.1 приведен график переходной характеристики h1(t), которая представляет собой ступенчатую функцию 1(t), пропорционально измененную в K раз.

Весовая функция пропорционального звена описывается следующим выражением

,

где δ(t) – дельта – функция или импульсная функция.

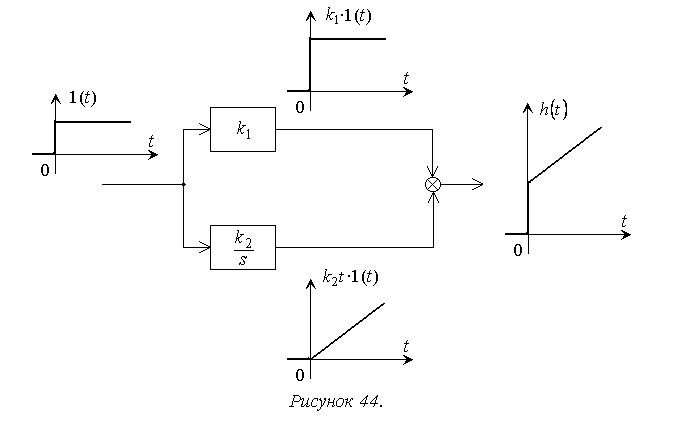
2.2.2. Интегрирующее звено

Интегрирующее звено описывается следующим дифференциальным уравнением:

Для нахождения переходной функции необходимо воспользоваться зависимостью Вычисляя это выражение, находим h2(t)=kּt.

Интегрирующее звено имеет передаточную функцию

где — коэффициент усиления интегрирующего звена, имеющий размерность с-1

Иногда вместо коэффициента k рассматривают параметр , который называется временем интегрирования.

Переходная функция интегрирующего звена

или

График переходной функции h2(t) представлен на рис.2.2. Для определения коэффициента K нужно найти значение ординаты h2(t) соответствующее моменту времени t=1, а для оценки постоянной интегрирования Т нужно найти значение момента времени, при котором h2(t)=1

Весовая функция, определяемая формулой будет

2.2.3. Инерционное (апериодическое) звено первого порядка

Инерционное звено или апериодическое первого порядка имеет передаточную функцию

,

где — коэффициент усиления, а — постоянная времени.

Переходная характеристика звена имеет вид

График показан на рис.2.3.

Переходная характеристика звена обладает следующими свойствами:

установившееся значение h3уст=lim h3(t) переходной функции h3(t) стремится к значению K :

касательная к h3(t) в точке t = 0 отсекает на линии установившегося значения h3уст отрезок, длина которого равна постоянной времени T;

значение функции h3(t) удовлетворяют соотношениям:

Для определения значений параметров K и Т по графику переходной функции h3(t) можно воспользоваться следующими формулами:

где значения моментов времени, соответствующие ординатам

Весовую функцию w3(t) можно определить, используя известную зависимость

.

Весовая функция также может быть найдена как обратное преобразование Лапласа от передаточной функции по формуле:

,

,

.

Вычислим весовую функцию звена, используя операторы пакета символьной математики Mathcad:

2.2.4. Реальное (инерционное) дифференцирующее звено

Реальное (инерционное) дифференцирующее звено имеет передаточную функцию

где — коэффициент усиления (или время дифференцирования); — постоянная времени инерционной части.

Переходная характеристика этого звена определяется

График h4(t) приведен на рис.2.4. Данная переходная функция обладает свойствами:

начальное значение h4(t=0)=h40 связано с параметрами К и Т соотношением ;

касательная к графику h4(t) в точке t=0 отсекает на оси времени отрезок, длина которого равна постоянной времени Т;

Для определения значений параметров Т и К графоаналитическим способом (по графику переходной функции h4(t)) следует воспользоваться соотношениями

Весовую функцию w4(t) можно определить, используя известную зависимость

.

Весовая функция также может быть найдена как обратное преобразование Лапласа от передаточной функции по формуле:

Вычислим весовую функцию звена, используя операторы пакета символьной математики Mathcad:

2.2.5. Интегро-дифференцирующее (реальное форсирующее) звено

Интегро-дифференцирующее или реальное форсирующее звено имеет передаточную функцию

,

где коэффициент усиления; постоянная времени форсирования; — постоянная времени инерционной части.

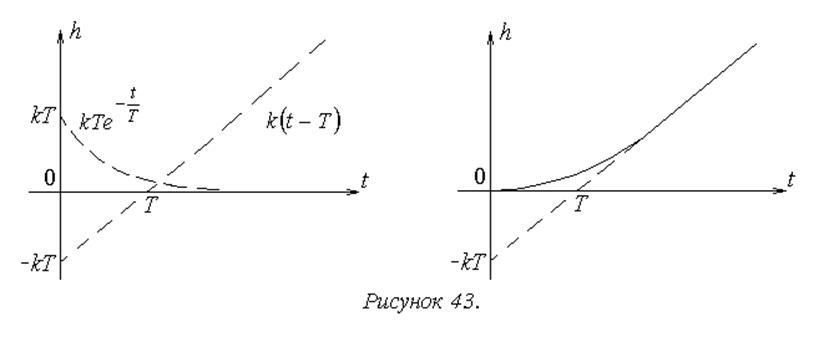
Переходная функция звена равна

,

где .

График переходной функции h5(t) при различных значениях l представлен на рис.2.5.

Переходная характеристика реального форсирующего звена обладает следующими свойствами:

установившееся значение переходной функции h5уст=lim h5(t) =K;

начальное значение h50=h5(t) связано с параметром λ следующим образом h50=K·λ;

ординаты разности в моменты времени принимают значения

Для определения значений параметров К, Т и l=t /Т по графику переходной характеристики h5(t) необходимо воспользоваться следующими соотношениями

Здесь значения моментов времени t, соответствующие ординатам

разность

Весовую функцию w5(t) можно определить, используя известную зависимость

.

Весовая функция также может быть найдена как обратное преобразование Лапласа от передаточной функции по формуле:

,

,

где .

Вычислим весовую функцию звена, используя операторы пакета символьной математики Mathcad:

2.3. Порядок выполнения работы

В соответствии с вариантом задания в табл.2.1. и табл.2.2. произвести построение временных характеристик типовых звеньев первого порядка и графоаналитическим способом рассчитать их параметры.

Вычисление временных характеристик звена или системы

Динамические свойства линейного звена характеризуются переходной h(t) или весовой w(t) функциями, которые связаны соотношениями

,

.

Связь между переходной и передаточной функциями определяется преобразованием Лапласа

Эти выражения показывают, что переходная и весовая функции содержат информацию о передаточной функции , которая в свою очередь также характеризует динамические свойства линейных звеньев.

По определению, переходной характеристикой h(t) называется реакция системы на единичное ступенчатое входное воздействие. Переходная характеристика вычисляется по формуле:

.

в программном пакете символьной математики Mathcad данная операция обратного преобразования Лапласа от выражения может быть реализована при помощи символьных операторов invlaplace, s, simplify, и оператора ограничения десятичных единиц до двух float,2.

Вычислим переходную характеристику звена, используя символьные операторы invlaplace, s (переводит выражение из области Лапласа в область времени по переменной S) и simplify (упрощает выражение):

Построение переходной характеристики звена или системы производится при помощи графической панели Graph Toolbar и панели вида графического отображения Graph. При появлении поля для построения характеристики в левое окошко (рядом с осью ординат) вводится имя функции, которую необходимо построить (или нескольких при необходимости построения в одной плоскости), в нижнее окошко (под осью абсцисс) вводится аргумент функции, настройки масштаба, цены деления шкал, вид кривой, её цвет, толщина и др. выполняются двойным нажатием левой клавиши «мыши» на область построения.

Рис.2.6. Построение переходной характеристики при помощи графической панели Graph Toolbar

По определению, весовой функцией w(t) называется реакция системы на импульсное входное воздействие. Весовая характеристика может быть найдена как обратное преобразование Лапласа от передаточной функции по формуле:

Построение весовой функции звена w(t) в программном пакете символьной математики Mathcad производится при помощи графической панели Graph Toolbar и панели вида графического отображения Graph. Сложность состоит в правильном выборе масштаба отображения для выполнения дальнейших расчетов параметров звеньев и удобстве восприятия полученных графиков. Для выбора масштаба отображения временных характеристик и их начертаний зададим диапазон и шаг изменения аргумента t (времени), воспользовавшись знаком «многоточие», вызываемым с помощью символа «;»:

Далее из палитры Инструменты графиков вызовем поле декартовых координат (Ctrl+2), где в позиции на оси абсцисс запишем аргумент t, а на оси ординат – w(t) или h(t). Для удобства представления характеристик необходимо дважды «кликнуть» на редактируемый график.

2.4. Варианты заданий

2.4.1. Постройте и рассчитайте все динамические характеристики звеньев, изменяя коэффициенты, в соответствии с номером варианта.

Источник