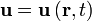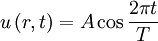Что такое волна в физике определение
Волны
Волна́ — изменение состояния среды (возмущение), распространяющееся в этой среде и переносящее с собой энергию. Другими словами: «…волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой физической величины, например, плотности вещества, напряжённости электрического поля, температуры [1] ».
Более правильное определение: Волна — это явление распространения в пространстве с течением времени возмущения физической величины.
Независимо от природы волны перенос энергии осуществляется без переноса вещества; последнее может возникнуть лишь как побочный эффект. Перенос энергии — принципиальное отличие волн от колебаний, в которых происходят лишь «местные» преобразования энергии. Волны же, как правило, способны удаляться на значительные расстояния от места своего возникновения. По этой причине волны иногда называют «колебанием, оторвавшимся от излучателя».
Большинство волн по своей природе являются не новыми физическими явлениями, а лишь условным названием для определённого вида коллективного движения. Так, если в объёме газа возникла звуковая волна, то это не значит, что в этом объёме появились какие-то новые физические объекты. Звук — это лишь название для особого скоординированного типа движения тех же самых молекул. То есть большинство волн — это колебания некоторой среды. Вне этой среды волны данного типа не существуют (например, звук в вакууме).
Имеются, однако, волны, которые являются не «рябью» какой-либо иной среды, а представляют собой именно новые физические сущности. Так, электромагнитные волны в современной физике — это не колебание некоторой среды (называвшейся в XIX веке эфиром), а самостоятельное, самоподдерживающееся поле, способное распространяться в вакууме. Аналогично обстоит дело и с волнами вероятности материальных частиц.
Некоторые явления также называют волнами, однако каждая из них обладают собственной спецификой. Так, с определёнными оговорками, говорят про: температурные волны, волны вероятности электрона и других частиц, волны горения, волны химической реакции, волны плотности реагентов, волны плотности транспортных потоков.
Отметим, что явления, выглядящие как волны, но не способные сами распространяться (как, например, песчаные дюны), волнами не являются.
Содержание
Характеристики волны
Временна́я и пространственная периодичности
В отличие от стационарного колебания волны имеют две основные характеристики:
Временная и пространственная периодичности взаимосвязаны, что отражено в законе дисперсии, который определяет, как именно волны будут выглядеть и распространяться. В упрощённом виде для линейных волн эта зависимость имеет следующий вид [2] :
где c — скорость распространения волны в данной среде.
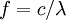
Интенсивность волны
О силе волны судят по её амплитуде. В отличие от колебания амплитуда волны — скалярная величина.
где A — амплитуда; k — коэффициент пропорциональности, зависящий от природы волны и свойств среды, где эта волна распространяется.
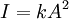
Классификации волн
Имеется множество классификаций волн, различающиеся по своей физической природе, по конкретному механизму распространения, по среде распространения и т. п.
В зависимости от физической среды, в которой распространяются волны, их свойства различны и поэтому различают:
По виду фронта волны (поверхности равных фаз):
По демонстрируемым волнами физическим проявлениям:
По постоянству во времени различают:
Волновые уравнения
Математическое описание волн основывается на представлении о них, как о пространственно распространяющихся колебаниях, и в общем виде записывается:
Более определённый вид уравнения зависит от типа волны.
Гармоническая волна
Изменение колеблющейся величины u для гармонически распространяющейся волны в любой точке описывается формулой:
или 
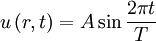
где A — амплитуда, t — время, а T — период волны.
В любой другой точке, расположенной на расстоянии r от первой в направлении распространения волны, изменение u происходит с опозданием на время t1 :
где c — скорость распространения волны в данной среде.
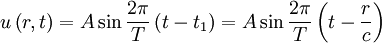
Лучи волны
Лучом волны называется линия, направление которой совпадает с направлением потока энергии в этой волне в каждой её точке. Например, плоской волне (см. раздел «Классификация волн») соответствует пучок параллельных прямых лучей; сферической волне — радиально расходящийся пучок лучей.
Расчёт формы лучей при небольшой длине волны — по сравнению с препятствиями, поперечными размерами фронта волны, расстояниями до схождения волн и т. п. — позволяет упростить сложный расчёт распространения волны. Это применяется в геометрической акустике и геометрической оптике.
Происхождение волн
Волны могут генерироваться различными способами.
Общие свойства волн
Распространение в однородных средах
При распространении волн изменения их амплитуды и скорости в пространстве и времени зависят от свойств анизотропности среды, сквозь которую проходят волны.
Чаще волны в некоторой среде затухают, что связано с диссипативными процессами внутри среды. Но в случае некоторых специальным образом подготовленных метастабильных сред амплитуда волны может, наоборот, усиливаться (пример: генерация лазерного излучения).
На практике монохроматические волны встречаются очень редко. Поэтому наряду с фазовой скоростью волны используется и понятие групповой скорости, то есть скорость «центра тяжести» волнового пакета.
Групповая и фазовая скорости совпадают только для линейных волн. Для нелинейных волн групповая скорость может быть как больше, так и меньше фазовой скорости. Однако когда речь идёт о скоростях, близких к скорости света, проявляется заведомое неравноправие между групповой и фазовой скоростями. Фазовая скорость не является ни скоростью движения материального объекта, ни скоростью передачи данных, поэтому она может превышать скорость света, не приводя при этом ни к каким нарушениям теории относительности. Групповая же скорость характеризует скорость движения сгустка энергии, переносимой волновым пакетом, и потому не должна превышать скорость света. Однако при распространении волны в метастабильной среде удаётся в определённых случаях добиться групповой скорости, превышающей скорость света.
Поскольку волна переносит энергию и импульс, то её можно использовать для передачи информации. При этом возникает вопрос о максимально возможной скорости передачи информации с помощью волн данного типа (чаще всего речь идёт об электромагнитных волнах). При этом скорость передачи информации никогда не может превышать скорости света, что было подтверждено экспериментально даже для волн, в которых групповая скорость превышает скорость света.
Пространственные размеры волны
Когда говорят о пространственном размере волны, то имеют в виду размер той области пространства, где амплитуду колебания нельзя считать (в рамках рассматриваемой задачи) пренебрежимо малой. Большинство волн могут, теоретически, обладать сколь угодно большим размером, как в направлении движения, так и поперёк него. В реальности же все волны обладают конечными размерами. Продольный размер волны, как правило, определяется длительностью процесса излучения волны. Поперечный же размер определяется рядом параметров: размером излучателя, характером распространения волны (например, плоская, сферически расходящаяся волна и т. д.).
Некоторые виды волн, в частности, солитоны, являются ограниченными волнами по построению.
Поляризация волн
Если в поперечной волне нарушается симметрия распределения возмущений (например, напряжённость электрического и магнитного полей в электромагнитных волнах) относительно направления её распространения, то мы имеем дело с поляризованной волной. В продольной волне поляризация возникнуть не может, т. к. распространение возмущения всегда совпадает с направлением распространения волны.
Подробней на эту тему см. статью «Поляризация волн».
Взаимодействие с телами и границами раздела сред
Если на пути волны встречается какой-либо дефект среды, тело или граница раздела двух сред, то это приводит к искажению нормального распространения волны. В результате этого часто наблюдаются следующие явления:
Конкретные эффекты, возникающие при этих процессах, зависит от свойств волны и характера препятствия.
Наложение волн
Излучения с разной длиной волны, но одинаковые по физической природе, могут взаимодействовать друг с другом, интерферировать. При этом могут возникнуть следующие частные эффекты:
Конечный результат проявления от встречи волн зависит от их свойств: физической природы, когерентности, поляризации и т. д.
Волна
Бернулли · Эйлер · Коши · Стокс · Навье
Система из двух нейтронных звезд порождает среду — «рябь» пространства-времени
Волны на поверхности воды
Более правильное определение: Волна — это явление распространения в пространстве с течением времени возмущения физической величины.
Большинство волн по своей природе являются не новыми физическими явлениями, а лишь условным названием для определённого вида коллективного движения. Так, если в объёме газа возникла звуковая волна, то это не значит, что в этом объёме появились какие-то новые физические объекты. Звук — это лишь название для особого скоординированного типа движения тех же самых молекул. То есть большинство волн — это колебания некоторой среды. Вне этой среды волны данного типа не существуют (например, звук в вакууме).
Имеются, однако, волны, которые являются не « рябью » какой-либо иной среды, а представляют собой именно новые физические сущности. Так, электромагнитные волны в современной физике — это не колебание некоторой среды (называвшейся в XIX веке эфиром), а самостоятельное, самоподдерживающееся поле, способное распространяться в вакууме. Аналогично обстоит дело и с волнами вероятности материальных частиц.
Отметим, что явления, выглядящие как волны, но не способные сами распространяться (как, например, песчаные дюны ), волнами не являются.
Содержание
Характеристики волны
Временна́я и пространственная периодичности
В отличие от стационарного колебания волны имеют две основные характеристики:
Где: c — скорость распространения волны в данной среде.
Строго говоря, это равенство справедливо только для гармоничных волн.
Интенсивность волны
Но для количественной характеристики переносимой волной энергии используется вектор плотности потока энергии . Его направление совпадает с направлением переноса энергии, а абсолютная величина равна количеству энергии, переносимой волной за единицу времени через единичную площадку, перпендикулярную направлению вектора. При небольших амплитудах:
где — амплитуда; — коэффициент пропорциональности, зависящий от природы волны и свойств среды, где эта волна распространяется.
Классификации волн
Имеется множество классификаций волн, различающиеся по своей физической природе, по конкретному механизму распространения, по среде распространения и т.п.
Волны можно классифицировать:
По отношению к направлению колебаний частиц среды, в которой распространяется волна, выделяют:
По виду фронта волны (поверхности равных фаз):
Рис.1.
A = в глубоководном месте;
B = в мелкой воде; Краткое движение поверхностной частицы становится более плоским с уменьшающейся глубиной.
1 = Прогрессия волны;
2 = Гребень;
*3 = Корыто.
На Рис.1 показаны периодические волны, которые характеризуются гребнями (максимумы) и впадинами (минимумами), и могут обычно категоризироваться как или продольные или поперечные.
Когда объект подпрыгивает на ряби в водоёме, то вектор движения точек волны происходит по орбитальной траектории. Появляющаяся рябь — не простые поперечные синусоидальные волны.
Все волны имеют общее поведение со множеством стандартных ситуаций.
По демонстрируемым волнами физическим проявлениям их можно разделить на:
По постоянству во времени различают:
Происхождение волн
Волны могут генерироваться различными способами.
Общие свойства волн
Распространение в однородных средах
При распространении волн изменения их амплитуды и скорости в пространстве и времени зависят от свойств анизотропности среды, сквозь которую проходят волны.
Чаще волны в некоторой среде затухают, что связано с диссипативными процессами внутри среды. Но в случае некоторых специальным образом подготовленных метастабильных сред амплитуда волны может, наоборот, усиливаться (пример: генерация лазерного излучения ).
Групповая и фазовая скорости совпадают только для линейных волн. Для нелинейных волн групповая скорость может быть как больше, так и меньше фазовой скорости. Однако когда речь идёт о скоростях, близких к скорости света, проявляется заведомое неравноправие между групповой и фазовой скоростями. Фазовая скорость не является ни скоростью движения материального объекта, ни скоростью передачи данных, поэтому она может превышать скорость света, не приводя при этом ни к каким нарушениям теории относительности. Групповая же скорость характеризует скорость движения сгустка энергии, переносимой волновым пакетом, и потому не должна превышать скорость света. Однако при распространении волны в метастабильной среде удаётся в определённых случаях добиться групповой скорости, превышающей скорость света.
Поскольку волна переносит энергию и импульс, то её можно использовать для передачи информации. При этом возникает вопрос о максимально возможной скорости передачи информации с помощью волн данного типа (чаще всего речь идёт об электромагнитных волнах). При этом скорость передачи информации никогда не может превышать скорости света, что было подтверждено экспериментально даже для волн, в которых групповая скорость превышает скорость света.
Пространственные размеры волны
Когда говорят о пространственном размере волны, то имеют в виду размер той области пространства, где амплитуду колебания нельзя считать (в рамках рассматриваемой задачи) пренебрежимо малой. Большинство волн могут, теоретически, обладать сколь угодно большим размером, как в направлении движения, так и поперёк него. В реальности же все волны обладают конечными размерами. Продольный размер волны, как правило, определяется длительностью процесса излучения волны. Поперечный же размер определяется рядом параметров: размером излучателя, характером распространения волны (например, плоская, сферически расходящаяся волна и т. д.).
Поляризация волн
Если в поперечной волне нарушается симметрия распределения возмущений (например, напряжённость электрического и магнитного полей в электромагнитных волнах) относительно направления её распространения, то мы имеем дело с поляризованной волной. В продольной волне поляризация возникнуть не может, т. к. распространение возмущения всегда совпадает с направлением распространения волны.
Подробней на эту тему см. статью «Поляризация волн».
Взаимодействие с телами и границами раздела сред
Если на пути волны встречается какой-либо дефект среды, тело или граница раздела двух сред, то это приводит к искажению нормального распространения волны. В результате этого часто наблюдаются следующие явления:
Конкретные эффекты, возникающие при этих процессах, зависит от свойств волны и характера препятствия.
Наложение волн
Излучения с разной длиной волны, но одинаковые по физической природе, могут взаимодействовать друг с другом, интерферировать. При этом могут возникнуть следующие частные эффекты:
Конечный результат проявления от встречи волн зависит от их свойств: физической природы, когерентности, поляризации и т. д.
Виды волн
Классифицированные волны можно в основном представить как:
Математические описания волн
Математическое описание волн основывается на представлении о них, как о пространственно распространяющихся колебаниях, и в общем виде записывается:
где — отклонение от некоего среднего положения в точке во время .
Более определённый вид уравнения зависит от типа волны.
Синусоидалные волны
Схема графика синусоидальной волны
Единицы полуамплитуды зависят от типа волны — волн, выраженных через амплитуду как расстояние, например в метрах, от звуковых волн, выраженных через давление и электромагнитных волн, выраженных через амплитуду электрической области (вт/метр).
Волны синуса соответствуют простому гармоническому движению.
Различные местные длины волны на основании гребня-к-гребню в океанской волне, приближающейся к берегу. [4]
Длина волны может быть полезным понятием, даже если волна не является периодической. Например, в океанской волне, приближающейся к берегу, показанному на фигуре, поступающая волна взаимодействует с переменной местной длиной волны, которая зависит частично от глубины морского дна по сравнению с высотой волны. Анализ волны может быть основанным на сравнении местной длины волны с местной водной глубиной. [5]
Уравнение волны
В частности рассмотрим уравнение волны в одном измерении, например, в применении к множеству волн. Предположим, что одномерная волна движется по оси X со скоростью v и амплитудой u (которая, вообще, зависит и от x и от t), уравнение волны:
Скорость v зависит от среды, через которую перемещается волна.
Эта формула представляет две формы волны, движущейся через среду в противоположных направлениях:
Смодулированные волны
Постоянная волна
Постоянная волна, известная как постоянная волна, является волной, которая остаётся в постоянном положении. Это явление произходит тогда, когда среда перемещается в противоположном направлении к волне, или это может возникнуть в постоянной среде в результате вмешательства между двумя волнами, движущихся в противоположных напправлениях.
Сумма двух противоположно движущихся волн (равной амплитуды и частоты) создает постоянную волну. Постоянные волны обычно возникают, когда граница блокирует дальнейшее распространение волны, таким образом вызывая отражение волны, и поэтому вводя противоположнодвижущуюся волну. В экстремальных точках, две противоположных волны находятся в антифазе и отменяют друг друга, производя узел. На полпути между двумя узлами есть антиузел, где две противоразмножающихся волны увеличивают друг друга максимально. Нет в среднем положении никакого чистого распространения энергии <среднее число>.
Вибрационные волны
Скорость волны, распространняющаяся по вибрирующему множеству волн («веренице») (v) напрямую пропорциональна квадратному корню напряженности множества волн («вереницы») (T) по линейной массовой плотности (μ):
Гармоническая волна
Изменение колеблющейся величины для гармонически распространяющейся волны в любой точке описывается формулой:
или
где — амплитуда, — время, а — период волны.
В любой другой точке, расположенной на расстоянии от первой в направлении распространения волны, изменение происходит с опозданием на время :
где — скорость распространения волны в данной среде.
Лучи волны
Лучом волны называется линия, направление которой совпадает с направлением потока энергии в этой волне в каждой её точке. Например, плоской волне (см. раздел «Классификация волн») соответствует пучок параллельных прямых лучей; сферической волне — радиально расходящийся пучок лучей.
Расчёт формы лучей при небольшой длине волны — по сравнению с препятствиями, поперечными размерами фронта волны, расстояниями до схождения волн и т. п. — позволяет упростить сложный расчёт распространения волны. Это применяется в геометрической акустике и геометрической оптике.