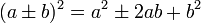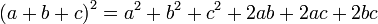Что такое возведение в квадрат
Быстрое возведение чисел в квадрат без калькулятора
Сегодня мы научимся быстро без калькулятора возводить большие выражения в квадрат. Под большими я подразумеваю числа в пределах от десяти до ста. Большие выражения крайне редко встречаются в настоящих задачах, а значения меньше десяти вы и так умеете считать, потому что это обычная таблица умножения. Материал сегодняшнего урока будет полезен достаточно опытным ученикам, потому что начинающие ученики просто не оценят скорость и эффективность этого приема.
Для начала давайте разберемся вообще, о чем идет речь. Предлагаю для примера сделать возведение произвольного числового выражения, как мы обычно это делаем. Скажем, 34. Возводим его, умножив само на себя столбиком:
1156 — это и есть квадрат 34.
Проблему данного способа можно описать двумя пунктами:
1) он требует письменного оформления;
2) в процессе вычисления очень легко допустить ошибку.
Сегодня мы научимся быстрому умножению без калькулятора, устно и практически без ошибок.
Итак, приступим. Для работы нам потребуется формула квадрата суммы и разности. Давайте запишем их:
Например, 28 можно представить в следующем виде:
Аналогично представляем оставшиеся примеры:
Аналогично выбираем варианты и для остальных примеров:
Можете самостоятельно попробовать рассчитать оба разложения, и вы убедитесь, что разложение с наименьшим вторым слагаемым считается проще. А мы перейдем к примерам, которые посчитаем без калькулятора:
Вот так за три минуты мы сделали умножение восьми примеров. Это меньше 25 секунд на каждое выражение. В реальности после небольшой тренировки вы будете считать еще быстрее. На подсчет любого двухзначного выражения у вас будет уходить не более пяти-шести секунд.
Но и это еще не все. Для тех, кому показанный прием кажется недостаточно быстрым и недостаточно крутым, предлагаю еще более быстрый способ умножения, который однако работает не для всех заданий, а лишь для тех, которые на единицу отличаются от кратных 10. В нашем уроке таких значений четыре: 51, 21, 81 и 39.
Казалось бы, куда уж быстрее, мы и так считаем их буквально в пару строчек. Но, на самом деле, ускориться можно, и делается это следующим образом. Записываем значение, кратное десяти, которое наиболее близкое нужному. Например, возьмем 51. Поэтому для начала возведем пятьдесят:
Значения, кратные десяти, поддаются возведению в квадрат намного проще. А теперь к исходному выражению просто добавляем пятьдесят и 51. Ответ получится тот же самый:
И так со всеми числами, отличающимися на единицу.
Если значение, которое мы ищем, больше, чем то, которое мы считаем, то к полученному квадрату мы прибавляем числа. Если же искомое число меньше, как в случае с 39, то при выполнении действия, из квадрата нужно вычесть значение. Давайте потренируемся без использования калькулятора:
Как видите, во всех случаях ответы получаются одинаковыми. Более того, данный прием применим к любым смежным значениям. Например:
При этом нам совсем не нужно вспоминать выкладки квадратов суммы и разности и использовать калькулятор. Скорость работы выше всяких похвал. Поэтому запоминайте, тренируйтесь и используйте на практике.
Ключевые моменты
С помощью этого приема вы сможете легко делать умножение любых натуральных чисел в пределах от 10 до 100. Причем все расчеты выполняются устно, без калькулятора и даже без бумаги!
Для начала запомните квадраты значений, кратных 10:
Далее — выкладки квадрата суммы или разности, в зависимости от того, к какому опорному значению ближе наше искомое выражение. Например:
Как считать еще быстрее
Но это еще не все! С помощью данных выражений моментально можно сделать возведение в квадрат чисел, «смежных» с опорными. Например, мы знаем 152 (опорное значение), а надо найти 142 (смежное число, которое на единицу меньше опорного). Давайте запишем:
Обратите внимание: никакой мистики! Квадраты чисел, отличающиеся на 1, действительно получаются из умножения самих на себя опорных чисел, если вычесть или добавить два значения:
— это и есть формула.
— аналогичная формула для чисел, больших на 1.
Надеюсь, данный прием сэкономит вам время на всех ответственных контрольных и экзаменах по математике. А у меня на этом все. До встречи!
Быстрое возведение чисел от 1 до 100 в квадрат
Вдохновленный этой статьей, решил поделиться с вами способом быстрого возведения в квадрат. Возведение в квадрат более редкая операция, нежели умножение чисел, но под нее существуют довольно интересные правила.

*квадраты до сотни
Для того, чтобы бездумно не возводить в квадрат по формуле все числа, нужно максимально упростить себе задачу следующими правилами.
Правило 1 (отсекает 10 чисел)
Для чисел, оканчивающихся на 0.
Если число заканчивается на 0, умножить его не сложнее, чем однозначное число. Стоит лишь дописать пару нулей.
В таблице отмечены красным.
Правило 2 (отсекает 10 чисел)
Для чисел, оканчивающихся на 5.
Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно умножить первую цифру (x) на (x+1) и дописать к результату “25”.
В таблице отмечены зеленым.
Правило 3 (отсекает 8 чисел)
Для чисел от 40 до 50.
Достаточно трудно, верно? Давайте разберем пример:
В таблице отмечены светло-оранжевым.
Правило 4 (отсекает 8 чисел)
Для чисел от 50 до 60.
Тоже достаточно трудно для восприятия. Давайте разберем пример:
В таблице отмечены темно-оранжевым.
Правило 5 (отсекает 8 чисел)
Для чисел от 90 до 100.
Похоже на правило 3, но с другими коэффициентами. Давайте разберем пример:
В таблице отмечены темно-темно-оранжевым.
Правило №6 (отсекает 32 числа)
Необходимо запомнить квадраты чисел до 40. Звучит дико и трудно, но на самом деле до 20 большинство людей знают квадраты. 25, 30, 35 и 40 поддаются формулам. И остается лишь 16 пар чисел. Их уже можно запомнить при помощи мнемоники (о которой я также хочу рассказать позднее) или любыми другими способами. Как таблицу умножения 🙂
В таблице отмечены синим.
Вы можете запомнить все правила, а можете запомнить выборочно, в любом случае все числа от 1 до 100 подчиняются двум формулам. Правила же помогут, не используя эти формулы, быстрее посчитать больше 70% вариантов. Вот эти две формулы:
Формулы (осталось 24 числа)
Для чисел от 25 до 50
Для чисел от 50 до 100
Конечно не стоит забывать про обычную формулу разложения квадрата суммы (частный случай бинома Ньютона):
UPDATE
Произведения чисел, близких к 100, и, в частности, их квадраты, также можно вычислять по принципу «недостатков до 100»: 
Словами: из первого числа вычитаем «недостаток» второго до сотни и приписываем двузначное произведение «недостатков».
Для квадратов, соответственно, еще проще.
Возведение в квадрат, возможно, не самая полезная в хозяйстве вещь. Не сразу вспомнишь случай, когда может понадобиться квадрат числа. Но умение быстро оперировать числами, применять подходящие правила под каждое из чисел отлично развивает память и «вычислительные способности» вашего мозга.
Кстати, думаю, все читатели хабры знают, что 64^2 = 4096, а 32^2 = 1024.
Многие квадраты чисел запоминаются на ассоциативном уровне. Например, я легко запомнил 88^2 = 7744, из-за одинаковых чисел. У каждого наверняка найдутся свои особенности.
Две уникальные формулы я впервые нашел в книге «13 steps to mentalism», которая мало связана с математикой. Дело в том, что раньше (возможно, и сейчас) уникальные вычислительные способности были одним из номеров в сценической магии: фокусник рассказывал байку о том, как он получил сверхспособности и в доказательство этого моментально возводит числа до сотни в квадрат. В книге так же указаны способы возведения в куб, способы вычитания корней и кубических корней.
Если тема быстрого счета интересна — буду писать еще.
Замечания об ошибках и правки прошу писать в лс, заранее спасибо.
Свойства степеней. Действия со степенями
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n раз подряд»
a — основание степени;
n — показатель степени.
Читается такое выражение, как a в степени n
Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) само на себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:
2 — основание степени;
3 — показатель степени.
Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.
Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.
Задачка про миллион: представьте, что у вас есть миллион рублей. В начале каждого года вы зарабатываете на нем еще два. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.
Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:
Математики заскучали и решили все упростить:
Ответ: через четыре года у вас будет 81 миллион.
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).
Таблица квадратов натуральных чисел от 1 до 100
Таблица квадратов и таблица степеней.
Таблица квадратов представляет собой числа, которые возведены во вторую степень. Она используется для упрощения расчетов при возведении чисел во вторую степень.
Как пользоваться таблицей квадратов по схеме:
Чтобы возвести число в квадрат, нужно выбрать десятку и единицу числа, которое необходимо возвести во вторую степень, и на их пересечении будет число, которое получается за счет умножения этого числа на себя.
Например: рассмотрим на картинке ниже число 1849. Оно получилось за счет умножения числа 43 на 43 (43 во второй степени), в котором “4”- это десятка, а “3” – единица.
Или другой пример: число 4356 получилось за счет умножения числа 66 на 66 (66 во второй степени), в котором “6” сбоку – это десятка, а “6” сверху – единица.
Таблица квадратов:
Вторую степень называют “квадратом числа”. При этом умножение числа самого на себя происходит один раз (a · a).
Возведение в степень:
Возведение в степень – алгебраическое действие, при котором происходит умножение числа самого на себя столько раз, сколько указано в показателе.
Пример: 3 2 (три во второй степени) = 3 · 3 = 9, или
3 3 (три в третьей степени) = 3 · 3 · 3 = 27.
Таблица степеней:
Свойства степеней:
Произведение степеней. При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
6 2 · 6 4 = 6 2+4 = 6 6
Частное степеней. При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.
6 4 / 6 2 = 6 4 – 2 = 6 2
Возведение степени в степень. При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
(6 4 ) 6 = 6 4 · 6 = 6 24
Степень произведения. При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
Степень частного (дроби). Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй. При возведении в степень дроби нужно возвести в степень и числитель, и знаменатель.
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Мировая экономика
Справочники
Востребованные технологии
Поиск технологий
О чём данный сайт?
Настоящий сайт посвящен авторским научным разработкам в области экономики и научной идее осуществления Второй индустриализации России.
Он включает в себя:
– экономику Второй индустриализации России,
– теорию, методологию и инструментарий инновационного развития – осуществления Второй индустриализации России,
– организационный механизм осуществления Второй индустриализации России,
– справочник прорывных технологий.
Мы не продаем товары, технологии и пр. производителей и изобретателей! Необходимо обращаться к ним напрямую!
Мы проводим переговоры с производителями и изобретателями отечественных прорывных технологий и даем рекомендации по их использованию.
О Второй индустриализации
Осуществление Второй индустриализации России базируется на качественно новой научной основе (теории, методологии и инструментарии), разработанной авторами сайта.
Конечным результатом Второй индустриализации России является повышение благосостояния каждого члена общества: рядового человека, предприятия и государства.
Вторая индустриализация России есть совокупность научно-технических и иных инновационных идей, проектов и разработок, имеющих возможность быть широко реализованными в практике хозяйственной деятельности в короткие сроки (3-5 лет), которые обеспечат качественно новое прогрессивное развитие общества в предстоящие 50-75 лет.
Та из стран, которая первой осуществит этот комплексный прорыв – Россия, станет лидером в мировом сообществе и останется недосягаемой для других стран на века.
Урок 7. Возведение в квадрат в уме

В этом уроке разобраны методики и алгоритмы, позволяющие научиться этому навыку.
Квадрат суммы и квадрат разности
Одним из самых простых способов возведения двузначных чисел в квадрат является методика, основанная на использовании формул квадрата суммы и квадрата разности:
Для использования этого метода необходимо разложить двузначное число на сумму числа кратного 10 и числа меньше 10. Например:
Практически все методики возведения в квадрат (которые описаны ниже) основываются на формулах квадрата суммы и квадрата разности. Эти формулы позволили выделить ряд алгоритмов упрощающих возведение в квадрат в некоторых частных случаях.
Квадрат близкий к известному квадрату
Если число, возводимое в квадрат, находится близко к числу, квадрат которого мы знаем, можно использовать одну из четырех методик для упрощенного счета в уме:
На 1 больше:
Методика: к квадрату числа на единицу меньше прибавляем само число и число на единицу меньше.
На 1 меньше:
Методика: из квадрата числа на единицу больше вычитаем само число и число на единицу больше.
На 2 больше
Методика: к квадрату числа на 2 меньше прибавляем удвоенную сумму самого числа и числа на 2 меньше.
На 2 меньше
Методика: из квадрата числа на 2 больше вычитаем удвоенную сумму самого числа и числа на 2 больше.
Все эти методики можно легко доказать, выведя алгоритмы из формул квадрата суммы и квадрата разности (о которых сказано выше).
Квадрат чисел, заканчивающихся на 5
Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу приписываем 25.
Это верно и для более сложных примеров:
Квадрат чисел близких к 50
Считать квадрат чисел, которые находятся в диапазоне от 40 до 60, можно очень простым способом. Алгоритм таков: к 25 прибавляем (или вычитаем) столько, насколько число больше (или меньше) 50. Умножаем эту сумму (или разность) на 100. К этому произведению добавляем квадрат разности числа, возводимого в квадрат, и пятидесяти. Посмотрите работу алгоритма на примерах:
Квадрат трехзначных чисел
Возведение в квадрат трехзначных чисел может быть осуществлено при помощи одной из формул сокращенного умножения:
Нельзя сказать, что этот способ является удобным для устного счета, но в особо сложных случаях его можно взять на вооружение:
436 2 = (400+30+6) 2 = 400 2 + 30 2 + 6 2 + 2*400*30 + 2*400*6 + 2*30*6 = 160 000 + 900 + 36 + 24 000 + 4 800 + 360 = 190 096
Тренировка
Если вы хотите прокачать свои умения по теме данного урока, можете использовать следующую игру. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что числа каждый раз разные.
Перед тем как начать игру, рекомендуем зарегистрироваться, чтобы результат был сохранен в вашей истории, и вы смогли бы видеть собственный прогресс.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.