Что такое вращательное движение в физике определение
Двойкам нет
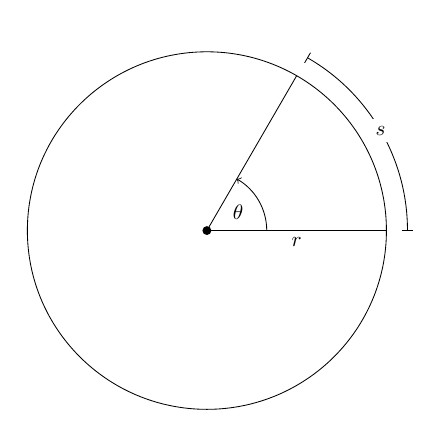
Вращательное движение — это движение тела, при котором точки описывают окружности, размещенные в параллельных плоскостях, причем центры всех окружностей располагаются на одной прямой, которая обычно определяется как ось вращения.
Вращательное движение представляет траекторию в виде кривой линии, а скорость в каждой точке кривой линии направлена по касательной.
Кинематика вращательного движения характеризуется:
Угловая скорость — это скорость вращательного движения, которая определяется отношением угла поворота радиуса, соединяющего движущееся тело с центром окружности, к времени, за которое был совершен поворот и записывается формулой: 

Единицу измерения угла поворота принято считать радианом, но не запрещается выражать его и в градусах. Размерность радиана:
Угловая скорость является векторной величиной, где его угловой вектор скорости направлен в том же направлении, что и поступательное движение правого винта (правило буравчика), где происходит движение по окружности.
Если вращательное движение совпадает с вращением рукоятки буравчика, то поступательное движение буравчика будет указывать на направление угловой скорости и углового ускорения, т.к. они сонаправлены.
Физический смысл угловой скорости при вращательном движении: угловая скорость будет равна углу поворота радиуса за единицу времени.
В Международной системе единиц угловая скорость имеет размерность — рад/с (радиан в секунду).
Связь между угловой и линейной скоростями: так как линейная скорость выражается следующей формулой 
Скорость во вращательном движении можно также выразить числом оборотов в единицу времени. Через число оборотов легко выразить угловую скорость, которая будет определяться формулой:
Число оборотов есть частота обращения, а величина обратная частоте есть период обращения и определяется формулой: 
Рассмотрим ускорение во вращательном движении: центростремительное ускорение и угловое ускорение.
Центростремительное ускорение — это такое ускорение, которое образуется при движении тела по окружности и направлено к центру по радиусу окружности. Центростремительное ускорение равно отношению квадрата скорости к радиусу окружности и записывается формулой:
Также центростремительное ускорение выражается в виде произведения линейной и угловой скоростей и записывается формулой:
Угловое ускорение — это ускорение, которое определяется отношением изменения угловой скорости ко времени, за которое произошло изменение этой скорости и записывается в виде формулы: 

Физический смысл углового ускорения: при вращательном движении угловое ускорение будет определяться как изменение угловой скорости за единицу времени.
Единицей углового ускорения в международной системе единиц является рад/с (радиан на секунду).
С изменением угловой скорости происходит изменение частоты вращения. Частота вращения характеризуется отношением числа оборотов ко времени и записывается в виде формулы:
Средняя частота вращения определяется соотношением:

Угловое ускорение имеет взаимосвязь с углом поворота. Эта связь определяется следующей формулой:
Вращательное движение
При выборе некоторых осей вращения, можно получить сложное вращательное движение — сферическое движение, когда точки тела движутся по сферам. При вращении вокруг неподвижной оси, не проходящей через центр тела или вращающуюся материальную точку, вращательное движение называется круговым.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
Простейшие механизмы — устройства, служащие для преобразования направления и величины (модуля) силы. Представляют собой элементы более сложных механизмов. Некоторые из простейших механизмов появились в глубокой древности.
Механи́ческим движе́нием тела называется изменение его положения в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики.
В физике, при рассмотрении нескольких систем отсчёта (СО), возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух системах отсчета (далее СО).
В физике механи́ческая эне́ргия описывает сумму потенциальной и кинетической энергий, имеющихся в компонентах механической системы. Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу; это энергия движения и сопровождающего его взаимодействия.
Вращательное движение тела. Закон вращательного движения
Основные понятия кинематики вращательного движения
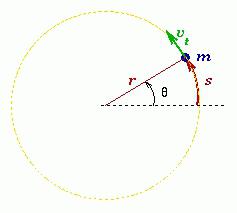
Вращательным движением материальной точки вокруг неподвижной оси называют такое движение, траекторией которого является окружность, находящаяся в плоскости перпендикулярной к оси, а центр ее лежит на оси вращения.
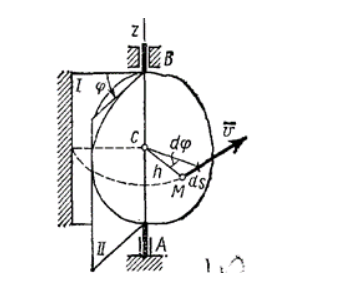
Пусть произвольное твердое тело T совершает вращения вокруг оси O, которая перпендикулярна плоскости рисунка. Выберем на данном теле точку M. При вращении эта точка будет описывать вокруг оси O круг радиусом r.
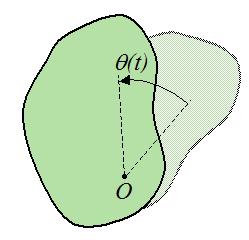
Через некоторое время радиус повернется относительно исходного положения на угол Δφ.
За положительное направление поворота принято направление правого винта (по часовой стрелке). Изменение угла поворота со временем называется уравнением вращательного движения твердого тела:
Основные элементы кинематики равномерного вращательного движения
Мерой перемещения материальной точки за небольшой промежуток времени dt служит вектор элементарного поворота dφ.
Если ω = dφ/dt = const, то такое движение называется равномерное вращательное движение. При нем угловую скорость определяют по формуле
Согласно предварительной формуле размерность угловой скорости
поэтому период вращения определим следующим образом:
Число оборотов, которое за единицу времени совершает тело, называется частотой вращения ν, которая равна:
Сравнивая формулы для угловой скорости и частоты вращения, получим выражение, связывающее эти величины:
Основные элементы кинематики неравномерного вращательного движения
Неравномерное вращательное движение твердого тела или материальной точки вокруг неподвижной оси характеризует его угловая скорость, которая изменяется со временем.
Вектор ε, характеризующий скорость изменения угловой скорости, называется вектором углового ускорения:
Если тело вращается, ускоряясь, то есть dω/dt > 0, вектор имеет направление вдоль оси в ту же сторону, что и ω.
Итак, в скалярном виде
Тангенциальное ускоренной материальной точки, которая выполняет вращательное движение
Момент импульса материальной точки
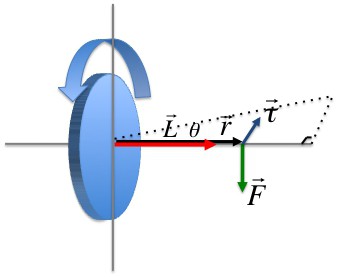
Векторное произведение радиуса-вектора траектории материальной точки массой mi на ее импульс называется моментом импульса этой точки касательно оси вращения. Направление вектора можно определить, воспользовавшись правилом правого винта.
Момент импульса материальной точки (Li) направлен перпендикулярно плоскости, проведенной через ri и υi, и образует с ними правую тройку векторов (то есть при движении с конца вектора ri к υi правый винт покажет направление вектора Li).
Учитывая, что при движении по кругу радиус-вектор и вектор линейной скорости для i-й материальной точки взаимно перпендикулярные,
Так что момент импульса материальной точки для вращательного движения примет вид
Момент силы, которая действует на i-ю материальную точку
Векторное произведение радиуса-вектора, который проведен в точку приложения силы, на эту силу называется моментом силы, действующей на i-ю материальную точку относительно оси вращения.
Величина li, равная длине перпендикуляра, опущенного из точки вращения на направление действия силы, называется плечом силы Fi.
Динамика вращательного движения
Уравнение динамики вращательного движения записывается так:
Формулировка закона следующая: скорость изменения момента импульса тела, которое совершает вращение вокруг неподвижной оси, равна результирующему моменту относительно этой оси всех внешних сил, приложенных к телу.
Момент импульса и момент инерции
Известно, что для i-й материальной точки момент импульса в скалярной форме задается формулой
Если вместо линейной скорости подставить ее выражение через угловую:
то выражение для момента импульса примет вид
Величина Ii = miri 2 называется моментом инерции относительно оси i-й материальной точки абсолютно твердого тела, проходящей через его центр масс. Тогда момент импульса материальной точки запишем:
Момент импульса абсолютно твердого тела запишем как сумму моментов импульса материальных точек, составляющих данное тело:
Момент силы и момент инерции
Закон вращательного движения гласит:
Известно, что представить момент импульса тела можно через момент инерции:
Учитывая, что угловое ускорение определяется выражением
получим формулу для момента силы, представленного через момент инерции:
Замечание. Момент силы считается положительным, если угловое ускорение, которым он вызван, больше нуля, и наоборот.
Теорема Штейнера. Закон сложения моментов инерции
Если система, которая совершает обороты округ неподвижной оси, состоит из n тел, то суммарный момент инерции такого типа системы будет равен сумме моментов, ее составляющих (закон сложения моментов инерции).
Вращательное движение
Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.
При выборе некоторых осей вращения, можно получить сложное вращательное движение — сферическое движение, когда точки тела движутся по сферам.
Содержание
Характеристики вращения тела
Кинематические характеристики
При равномерном вращении (T оборотов в секунду),
Динамические характеристики
Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Эта характеристика входит в дифференциальные уравнения, полученные из уравнений Гамильтона или Лагранжа. Кинетическую энергии вращения можно записать в виде 


где: mi — масса i-й точки, ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как масса тела является мерой его инертности в поступательном движении.
где Iz — момент инерции тела относительно оси вращения. 
См. также
Ссылки
Полезное
Смотреть что такое «Вращательное движение» в других словарях:
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ — твёрдого тела, 1) В. д. вокруг ос и движение тв. тела, при к ром к. л. две его точки А и В остаются всё время неподвижными (рис.). Прямая АВ, проходящая через эти точки, наз. осью вращения; все точки тела при В. д. описывают окружности в… … Физическая энциклопедия
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ — твердого тела, 1) вокруг оси движение, при котором все точки тела, лежащие на оси вращения, неподвижны, а остальные точки тела описывают окружности с центрами на оси. 2) Вокруг точки движение тела, при котором одна его точка О неподвижна, а все… … Современная энциклопедия
Вращательное движение — твердого тела, 1) вокруг оси движение, при котором все точки тела, лежащие на оси вращения, неподвижны, а остальные точки тела описывают окружности с центрами на оси. 2) Вокруг точки движение тела, при котором одна его точка О неподвижна, а все… … Иллюстрированный энциклопедический словарь
вращательное движение — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN rotary motionrotational motion … Справочник технического переводчика
Вращательное движение — твёрдого тела, 1) вращательное движение вокруг оси движение твёрдого тела, при котором какие нибудь две его точки А. и В остаются всё время неподвижными (см. рис.). Прямая AB, проходящая через эти точки, называется осью вращения; все… … Большая советская энциклопедия
вращательное движение — твёрдого тела, 1) вокруг оси движение, при котором все точки тела, лежащие на оси вращения, неподвижны, а остальные точки тела описывают окружности с центрами на оси; 2) вокруг точки движение тела, при котором одна его точка О неподвижна, а все … Энциклопедический словарь
вращательное движение — sukamasis judesys statusas T sritis automatika atitikmenys: angl. rotary motion; rotary movement vok. Drehbewegung, f; Rotation, f; Rotationsbewegung, f; umlaufende Bewegung, f rus. вращательное движение, n pranc. mouvement de rotation, m;… … Automatikos terminų žodynas
вращательное движение — sukamasis judėjimas statusas T sritis fizika atitikmenys: angl. rotary motion; rotational motion vok. Drehbewegung, f; Rotationsbewegung, f rus. вращательное движение, n pranc. mouvement de rotation, m; mouvement rotatoire, m … Fizikos terminų žodynas
вращательное движение — sukamasis judesys statusas T sritis Kūno kultūra ir sportas apibrėžtis Judesys, vykstantis (atliekamas) kūnui ar jo dalims sukantis apie tašką arba ašį. Viso kūno sukamasis judesys vyksta apie ašį, kuri gali būti kūno viduje arba už kūno. Tokių… … Sporto terminų žodynas
Поступательное и вращательное движение
Движение твердого тела разделяют на виды:
Первые два из них – простейшие, а остальные представляют как комбинацию основных движений.
Поступательное криволинейное движение. Угол поворота тела
Поступательным называют движение твердого тела, при котором любая прямая, проведенная в нем, двигается, оставаясь параллельной своему начальному направлению.
Прямолинейное движение является поступательным, но не всякое поступательное будет прямолинейным. При наличии поступательного движения путь тела представляют в виде кривых линий.
Свойства поступательного движения определяются теоремой: при поступательном движении все точки тела описывают одинаковые траектории и в каждый момент времени обладают одинаковыми по модулю и направлению значениями скорости и ускорения.
Следовательно, поступательное движение твердого тела определено движением любой его точки. Это сводится к задаче кинематики точки.
Понятие о скорости и ускорении тела имеют смысл только при наличии поступательного движения. В других случаях точки тела характеризуются разными скоростями и ускорениями.
Вращательное движение абсолютно твердого тела вокруг неподвижной оси – это движение всех точек тела, находящихся в плоскостях, перпендикулярных неподвижной прямой, называемой осью вращения, и описывание окружностей, центры которых располагаются на этой оси.
При наличии такого вращения значения углов поворота радиус-вектора различных точек тела будут аналогичны.
Вращательное и поступательное движение. Формулы
| Поступательное | Вращательное |
| Равномерное | |
| s = υ · t | φ = ω · t |
| υ = c o n s t | ω = c o n s t |
| a = 0 | ε = 0 |
| Равнопеременное | |
| s = υ 0 t ± a t 2 2 | φ = ω 0 t ± ε · t 2 2 |
| υ = υ 0 ± a · t | ω = ω 0 ± ε · t |
| a = c o n s t | ε = c o n s t |
| Неравномерное | |
| s = f ( t ) | φ = f ( t ) |
| υ = d s d t | ω = d φ d t |
| a = d υ d t = d 2 s d t 2 | ε = d ω d t = d 2 φ d t 2 |
Задачи на вращательное движение
Решение
Решение