Что такое время трогания электромагнита

Рабочий цикл электромагнита

Работа электромагнита в электромагнитном механизме носит циклический характер. Это определяется тем, что якорь электро­магнита, используемого в качестве привода, совершает поступа­тельное или вращательное перемещение в ограниченных пределах, следовательно, необходимо обеспечивать его возврат в исходное положение.

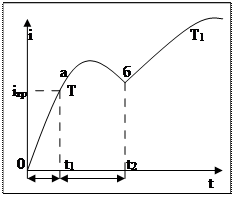
Первым этапом рабочего цикла (рис.4.12) является процесс сра­батывания электромагнита. Он начинается с момента подачи пита­ния на обмотку электромагнита, когда якорь переходит из своего начального положения в конечное (рис. 4.12, а) и подразделя­ется на период трогания якоря и период движения.

В период трогания ток в обмотке электромагнита на­растает до , обеспечивающего равенство электромагнитной силы силам, противодействующим движению. После этого якорь при­ходит в движение. Время трогания , в течение которого ток на­растает до тока трогания, определяется как схемой включения об­мотки электромагнита и условиями ее питания, так и параметрами самого электромагнита и его нагрузки.

Для одного и того же электромагнита при разной нагрузке (противодействующих движе­нию силах) время трогания будет различно. Характер движения зависит от соотношения движущих (элект­ромагнитных) и противодействующих сил, а также массы движу­щихся частей, трения и т. д.

В период движения при срабатывании совершается та работа, которую должен произвести электромагнит. Ток в обмотке электромагнита в процессе движения якоря, как правило, изменяется (кривая 2, рис.4.12, б). Его изменения связаны как с процессом установления тока в обмотке, который имел бы место при неподвижном якоре (кривая 1, рис. 4.12, б), так и возник­новением противоЭДС, связанной с движением якоря.

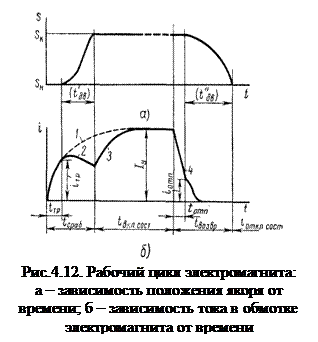
Период движения определяет время движения при срабатывании , кото­рое совместно со временем трогания составляет время срабатывания.

После окончания перемещения якоря следует период включенного состояния, в течение которого система находится в покое, а обмотка остается во включенном состоянии. В начальной стадии этого периода ток в обмотке электромагнита нарастает до установившегося значения (кривая 3, рис. 4.12, б), после чего, если не изменяются напряжение питания и сопротив­ление обмотки, ток остается неизменным.

Длительность включенного состояния зависит от требований эксплуатации электромагнита. Температура нагрева, которой достигает обмотка электромагнита в процессе включенного состояния, не должна превосходить допус­тимого значения.

Процесс возврата якоря в исходное состояние, так же как и срабатывание, происходит двумя ступенями. Сначала при отключении обмотки ток спадает до значения тока отпускания , при котором электромагнитная сила становится равной силе, стре­мящейся возвратить якорь в исходное положение. Длительность этого процесса характеризуется промежутком времени , зави­сящим от нагрузки, условий отключения обмотки и от задержива­ющего действия вихревых токов в массивных частях электромаг­нита и короткозамкнутых контурах, если такие имеются. Переме­щение подвижных частей в исходное положение происходит в те­чение времени , которое зависит от ряда факторов и, в первую очередь, от величины отбрасывающих якорь усилий.

Время отпус­кания и время движения в процессе возврата составляют время возврата .

Цикл работы электромагнита завершается периодом от­ключенного состояния, в течение которого обмотка электромагнита остается обесточенной и происходит ее охлаждение.

Источник

Динамика и время срабатывания электромагнитов

а) Время срабатывания. До сих пор мы рассматривали только статические характеристики электромагнитов, когда в их обмотке проходит неизменный ток, причем якорь либо неподвижен, либо якорь движется, но ток в обмотке не меняется по своему действующему значению, поскольку электромагнит имеет последовательную обмотку. В таком режиме работают тормозные и удерживающие электромагниты. В большинстве электромагнитов процесс имеет динамический характер. В этом случае после включения обмотки электромагнита происходит нарастание потока в магнитной цепи до тех нор, пока сила, развиваемая электромагнитом, не станет равна противодействующей силе. По достижении указанного равенства якорь начинает двигаться. При этом ток и поток меняются по весьма сложному закону, определяемому параметрами электромагнита и противодействующей силой. После того как якорь придет в свое конечное положение, ток и поток в электромагните будут продолжать изменяться до тех пор, пока не достигнут установившегося значения.

Рассмотрим более подробно все эти три стадии для электромагнита постоянного тока с параллельной обмоткой. Первая стадия — с момента подачи напряжения до начала трогания якоря. Начиная с момента включения обмотки и до момента начала движения якоря напряжение источника уравновешивается активным падением напряжения и противо– э. д. с. в катушке:

Так как в начальном положении якоря рабочий зазор имеет относительно большое значение, магнитная цепь может считаться ненасыщенной, а индуктивность обмотки— постоянной величиной. Поскольку потокосцепление уравнение можно преобразовать:

Решение этого уравнения относительно тока, как известно, имеет вид:

где установившееся значение тока;

постоянная времени цепи.

Величина тока, при котором начинается движение якоря, называется током трогания /_Тр, а время нарастания тока от нуля до /_Тр — временем трогания £_Тр.

Для момента трогания можно записать в виде

Решив относительно времени трогания, получим:

Таким образом, во-первых, время трогания пропорционально постоянной времени T, и, во-вторых, по мере приближения время трогания начинает быстро расти. Как только начинается движение якоря, зазор уменьшается и индуктивность увеличивается, поскольку Так как при движении якоря индуктивность изменяется, то примет вид:

При движении якоря поэтому величина тока

Рис. 5.1. Зависимость тока от времени

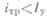
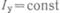
Имеется целый ряд методов расчета процессов в электромагните при движении якоря. Как показано на рис. 5.1, в динамике начало движения имеет место при токе . При движении якоря ток вначале еще немного нарастает, а затем падает до величины, меньшей тока трогания. Таким образом, в процессе движения якоря, когда зазор меняется от начального до конечного значения, величина тока в обмотке значительно меньше установившегося значения. Поскольку при движении якоря во всех точках его пути ток в обмотке меньше установившегося значения, то и сила, развиваемая электромагнитом, в динамике значительно меньше, чем в статике при . С этим необходимо считаться при согласовании силы тяги электромагнита и противодействующих сил.

Для ориентировочного определения времени движения можно воспользоваться статической характеристикой. На рис.5.2 изображены статическая тяговая характеристика электромагнита и характеристика противодействующей силы. Разность сил , идет на сообщение ускорения подвижным частям:

(5.9)

где масса подвижных частей, приведенная к рабочему зазору; перемещение якоря; скорость движения якоря.

После интегрирования получим:

Рис.5.2. Статическая тяговая характеристика электромагнита и характеристика противодействующей силы

Интеграл удобно рассчитывается графоаналитически. Скорость в точке хода б равна:

где масштаб по оси силы; масштаб по оси перемещения; площадь, пропорциональная работе движущей силы.

Зная скорость в любой точке хода, можно рассчитать время движения на всех участках и суммированием определить полное время движения.

Иногда во время движения ток мало меняется и составляет некоторую долю а от установившегося В таких случаях рекомендуется строить статическую характеристику при .

б) Ускорение и замедление срабатывания и отпускания электромагнита постоянного тока. Полное время срабатывания состоит из времени трогания и времени движения:

В большинстве случаев основную часть времени срабатывания составляет время трогания. Поэтому при ускорении и замедлении срабатывания воздействуют прежде всего на Согласно

Допустим, что ток трогания не меняется (неизменна сила противодействующей пружины). Рассмотрим влияние активного сопротивления цепи при неизменной величине индуктивности и питающего напряжения. После включения электромагнита ток в обмотке изменяется и скорость нарастания тока равна:

При уменьшении сопротивления R увеличивается установившийся ток и величина уменьшается.

Замедленное спадание потока создает выдержку времени при отпускании.

Для вторичной короткозамкнутой обмотки ненасыщенной системы в этом случае можно записать:

Поскольку величина зазора уменьшилась, индуктивность при притянутом якоре больше, чем при отпущенном L-i.

Решив относительно тока, получим:

Умножив обе части на G\ w₂, после преобразования получим:

Благодаря тому, что рабочий зазор в притянутом состоянии в десятки и даже сотни раз меньше, чем в отпущенном можно получить время трогания при отпускании до 10 сек, тогда как время трогания при притяжении составляет доли секунды.

При н. с, равной нулю, в цепи устанавливается поток, определяемый кривой размагничивания материала и воздушным зазором. Этот остаточный поток может создавать силу притяжения большую, чем сила, развиваемая пружиной. Произойдет залипание якоря. Для устранения залипания ставится немагнитная прокладка, снижающая величину остаточного потока.

В реальных конструкциях реле времени магнитная система при притянутом положении якоря сильно насыщена.

Для насыщенной цепи справедливо уравнение

Решив уравнение относительно времени, получим:

где поток, при котором сила, развиваемая пружиной, равна силе электромагнита.

Для определения значения интеграла рассчитывается зависимость потока в рабочем зазоре от н. с. После этого строится зависимость 1/ш=/(Ф) и графическим интегрированием решается.

в) Динамика электромагнитов переменного тока. Рассмотрим магнитную цепь электромагнита, у которого магнитопровод ненасыщен. Пусть включение происходит в нуль напряжения. В этом случае можно записать:

Поскольку цепь линейна, ток можно выразить через поток

Решив это уравнение относительно потока, найдем:

где Ф_т — максимальное значение потока.

Согласно (5.27) при / = 0 поток в системе также равен нулю. Через время t = n / u > поток достигает наибольшего значения, поскольку постоянная составляющая потока складывается с переменной составляющей. Если пренебречь затуханием, то через полпериода поток достигает величины, равной 2Ф_та.

По мере затухания постоянной составляющей потока пиковое значение потока будет уменьшаться, пока не достигнет Ф_т. Таким образом, в электромагните переменного тока наибольшие пиковые значения потока, а следовательно, и силы, будут иметь место в начале процесса включения, причем пиковое значение потока и силы наступает примерно через 0,01 сек после начала включения (при частоте тока 50 Гц). Это обеспечивает малое время трогания.

Если магнитная система насыщена, то возникновение постоянной составляющей потока в момент включения ведет к появлению большого сильно искаженного намагничивающего тока.

При включении в нуль тока (потока) постоянная составляющая не появляется и пиковое значение потока появляется через четверть периода после начала включения. Таким образом, и в этом случае обеспечивается быстрое срабатывание электромагнита без применения специальных мер.

Расчет динамических характеристик электромагнитов переменного тока аналитически очень затруднен. Эту задачу удается решить применением аналоговых счетных машин. Необходимо отметить, что в момент включения электромагнита рабочий зазор в магнитной цепи велик, что вызывает согласно большой намагничивающий ток, в десятки раз больший, чем ток в притянутом положении якоря.

Дата добавления: 2019-07-15 ; просмотров: 217 ; Мы поможем в написании вашей работы!

Источник

Время срабатывания и время отпускания электромагнитов. Способы изменения временных параметров электромагнита

Процесс срабатывания электромагнитов можно разделить на три части: 1) подача напряжения на обмотку и трогание якоря; 2) движение якоря; 3) конечное положение якоря. Смысл деления процесса на три части рассмотрим на характеристике I = f(t) для электромагнитов.

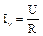
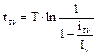
I-я часть /до точки «а»/: ток трогания i_тр→I_y, где – установившееся значение тока. Процесс динамический имеет решение относительно времени трогания:

, (21)

Рисунок 33 – Время срабатывания и работы электромагнита

где T = L/R – постоянная времени на участке «0…Т».

Зазор «δ» достаточно велик, магнитная цепь ненасыщенна и, следовательно, L_контур = L_обм ≈ const.

II часть: от точки «а» до точки «b».

Движение якоря уменьшает «δ» и при этом L_контур↑. Вначале ток незначительно увеличивается, а затем начинает уменьшаться с ↑L_контур до момента «b». Якорь достигает своего конечного положения.

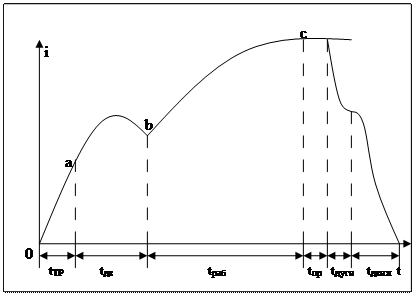
III часть: от точки «b» и далее. Происходит увеличение тока до i = I_у = U/R по закону:

, (22)

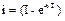
Время срабатывания электромагнита равно t_cp = t_тр + t_дв, причём t_тр > t_дв. Тяговое усилие Р_э→max при конечном положении якоря (i = I_y).

При отключении электромагнита от источника фиксируется время отпускания электромагнита t_отп:

где t_спад – время спадания потока до потока отпускания; t_дв – время движения.

Рисунок 34 – Время срабатывания и время отпускания электромагнита

Время срабатывания и отпускания электромагнита можно изменить включением дополнительного активного сопротивления последовательно или параллельно катушке электромагнита, использованием короткозамкнутого кольца (витка) на сердечнике электромагнита и другими способами, которые способны изменить постоянную времени электромагнита либо изменением L, R, либо изменением величины результирующего магнитного потока электромагнита.

Время срабатывания электромагнита можно уменьшить, включив активное сопротивление R последовательно с катушкой электромагнита, а время отпускания увеличить, включив параллельно катушке электромагнита активное или активно-емкостное сопротивление. Время отпускания можно увеличить, использовав короткозамкнутый виток или кольцо, в котором при отключении источника возникает магнитный поток самоиндукции, поддерживающий спадающий основной магнитный поток до величины, способной удержать якорь электромагнита притянутым к сердечнику дополнительное время.

Дата добавления: 2016-01-16 ; просмотров: 3139 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

ДИНАМИКА И ВРЕМЯ СРАБАТЫВАНИЯ ЭЛЕКТРОМАГНИТОВ

а) Время срабатывания. До сих пор мы рассматри­вали только статические характеристики электромагни­тов, когда в их обмотке проходит неизменный ток, при­чем якорь либо неподвижен, либо якорь движется, но ток в обмотке не меняется по своему действующему зна­чению, поскольку электромагнит имеет последователь­ную обмотку. В таком режиме работают тормозные и удерживающие электромагниты. В большинстве электромагнитов процесс имеет динамический характер. В этом случае после включения обмотки электромагнита про­исходит нарастание потока в магнитной цепи до тех нор, пока сила, развиваемая электромагнитом, не станет рав­на противодействующей силе. По достижении указанно­го равенства якорь начинает двигаться. При этом ток и поток меняются по весьма сложному закону, определяе­мому параметрами электромагнита и противодействую­щей силой. После того как якорь придет в свое конеч­ное положение, ток и поток в электромагните будут про­должать изменяться до тех пор, пока не достигнут уста­новившегося значения.

Рассмотрим более подробно все эти три стадии для электромагнита постоянного тока с параллельной обмот­кой. Первая стадия — с момента подачи напряжения до начала трогания якоря. Начиная с момента включения обмотки и до момента начала движения якоря напряже­ние источника уравновешивается активным падением на­пряжения и противо– э. д. с. в катушке:

. (5.2)

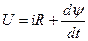
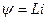
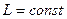
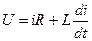
Так как в начальном положении якоря рабочий зазор имеет относительно большое значение, магнитная цепь может считаться ненасыщенной, а индуктивность обмот­ки— постоянной величиной. Поскольку потокосцепление и уравнение можно преобразовать:

. (5.4)

Решение этого уравнения относительно тока, как из­вестно, имеет вид:

, (5.5)

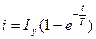
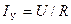
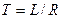
где –установившееся значение тока;

–постоянная времени цепи.

Величина тока, при котором начинается движение якоря, называется током трогания , а время нараста­ния тока от нуля до , временем трогания .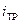

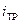
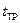
Для момента трогания можно записать в виде

. (5.6)

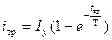
Решив относительно времени трогания, получим:

. (5.7)

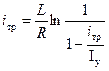
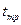
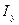
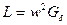
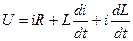
Таким образом, во-первых, время трогания пропорцио­нально постоянной времени T, и, во-вторых, по мере при­ближения к время трогания начинает быстро расти. Как только начинается движение якоря, зазор умень­шается и индуктивность увеличивается, поскольку . Так как при движении якоря индуктивность изменяется, то примет вид:

.(5.8)

При движении якоря , поэтому величина тока и начинают уменьшаться, поскольку сумма всех падений напряжения равна неизменному значению на­пряжения источника U. Зависимость тока от времени показана на рис. 5.1. Чем больше скорость движения якоря, тем боль­ше спад тока. В точке b якорь до­стиг своего крайнего положения и уменьшение тока прекратилось. По­сле остановки якоря ток будет уве­личиваться до тех пор, пока не до­стигнет установившегося значения причем постоянная времени будет больше, чем , посколь­ку конечный зазор меньше, чем начальный зазор . 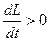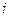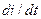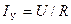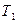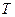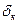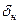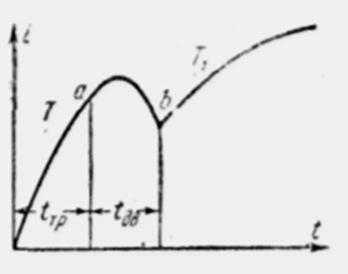Так как в притянутом положении якоря рабочий зазор мал, то возможно насыщение магнитной системы, и за­кон нарастания тока будет отличаться от экспоненци­ального, что необходимо учитывать при расчете времени установления потока.

Рис. 5.1. Зависимость тока от времени

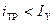
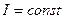
Имеется целый ряд методов расчета процессов в электромагните при движении якоря. Как показано на рис. 5.1, в динамике начало движения имеет место при токе . При движении якоря ток вначале еще немного нарастает, а затем пада­ет до величины, меньшей то­ка трогания. Таким образом, в процессе движения якоря, когда зазор меняется от на­чального до конечного зна­чения, величина тока в об­мотке значительно меньше установившегося значения. Поскольку при движении якоря во всех точках его пу­ти ток в обмотке меньше установившегося значения, то и сила, развиваемая электромагнитом, в динамике значительно меньше, чем в статике при . С этим необходимо считаться при согласовании силы тяги элек­тромагнита и противодействующих сил.

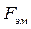
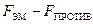
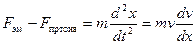
Для ориентировочного определения времени движе­ния можно воспользоваться статической характеристи­кой. На рис.5.2 изображены статическая тяговая ха­рактеристика электромагнита и характеристика про­тиводействующей силы. Разность сил , идет на сообщение ускорения подвижным частям:

, (5.9)

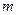
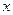
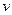
где –масса подвижных частей, приведенная к рабочему зазору; –перемещение якоря; –скорость движения якоря.

После интегрирования получим:

. (5.10)

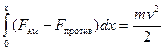
Интеграл удобно рассчитывается графоаналитически. Скорость в точке хода б равна:

, (5.11)

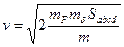
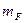
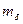
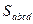
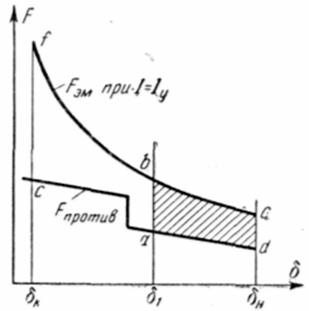где — масштаб по оси силы; — масштаб по оси перемещения; -площадь, пропорциональная работе движущей силы.

Рис.5.2. Статическая тяговая ха­рактеристика электромагнита и характеристика про­тиводействующей силы

Зная скорость в любой точке хода, можно рассчитать время движения на всех участках и суммированием определить полное время движения.

Иногда во время движения ток мало меняется и со­ставляет некоторую долю от установившегося. В таких случаях рекомендуется строить статическую ха­рактеристику при .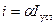

б) Ускорение и замедление срабатывания и отпуска­ния электромагнита постоянного тока. Полное время срабатывания состоит из времени трога­ния и времени движения:

. (5.12)

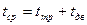
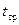
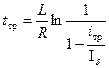
В большинстве случаев основную часть времени сраба­тывания составляет время трогания. Поэтому при уско­рении и замедлении срабатывания воздействуют прежде всего на . Согласно

. (5.13)

Допустим, что ток трогания не меняется (неизменна си­ла противодействующей пружины). Рассмотрим влияние активного сопротивления цепи при неизменной величине индуктивности и питающего напряжения. После включе­ния электромагнита ток в обмотке изменяется и скорость нарастания тока равна:

. (5.14)

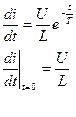
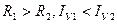
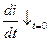
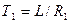
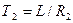
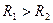
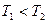
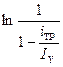
Таким образом, скорость нарастания тока в момент включения не зависит от активного сопротивления цепи и определяется только питающим напряжением и индук­тивностью цепи. Изменение тока во времени для двух значений активного сопротивления цепи показано на рис.5.3. Поскольку . Обе кривые в начале координат имеют общую касательную, так как не зависит от активного сопротивления. Постоянная времени для первого случая для второго ; так как то . При уменьшении сопротивления R увеличивается установившийся ток и величина уменьшается.

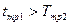
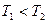
Можно показать, что логарифм уменьшается быстрее, чем растет постоянная времени Т. В результате , несмотря на то, что . Чем меньше активное сопротивление цепи, тем быстрее будет срабатывать электромагнит.

При уменьшении активного сопротивления обмотки растет мощность Р, потребляемая ею:

.

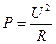
Для ограничения температуры нагрева необходимо развивать у катушки поверхность охлаждения, т. е. ее размеры. Увеличение размеров обмотки потребует уве­личения размеров магнитопровода.

Для ограничения разме­ров электромагнита в насто­ящее время широко приме­няется форсировка по схеме рис. 5.4. В отключенном по­ложении сопротивление 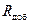шунтировано размыкаю­щим контактом, связанным с якорем электромагнита.

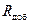
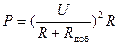
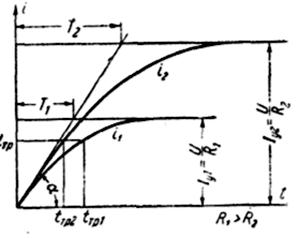После замыкания контакта К малое сопротивление обмотки R способствует быстрому нарастанию тока до тока трогания. После начала движе­ния якоря контакт размыкается и в цепь вводится сопро­тивление , благодаря чему ограничивается мощность Р, выделяемая в обмотке:

(5.15)

Рис.5.3 Изменение тока во времени для двух значений активного сопротивления

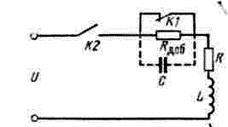Рис.5.4. Схема форсировки электромагнита

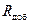
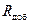
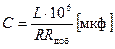
Иногда для ускорения срабатывания сопротивление шунтируют конденсатором. В первый момент времени конденсатор уменьшает падение напряжения на этом со­противлении, благодаря чему обеспечивается форсировка электромагнита. В установившемся режиме величина то­ка в цепи ограничивается сопротивлением . Величи­ну емкости конденсатора в рекомендуется брать равной:

, (5.16)

где L— индуктивность обмотки, Гн, R-ее активное сопротивление, Ом, Rдоб— добавочное сопротивление, Ом.

Теперь рассмотрим влияние питающего напряжения на время трогания. При уменьшении питающего напря­жения уменьшается величина установившегося тока, что ведет к увеличению

.

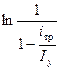
При время трогания .

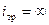
С ростом напряжения время трогания уменьшается в соответствии с уменьшением

.

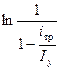
Иногда возникает необходимость ускорить срабаты­вание уже готового электромагнита. Увеличение питаю­щего напряжения без измене­ния активного сопротивления цепи ведет к ускорению сраба­тывания, но катушка электро­магнита может сгореть, если при номинальном значении пи­тающего напряжения темпера­тура обмотки равна предельно допустимой. В этих случаях рекомендуется при повышении питающего напряжения в цепь включать добавочное сопротивление, чтобы величина установившегося тока оставалась неизменной и равной I_у. При этом ускорение срабатывания происходит за счет уменьшения постоянной времени. Величина

остается неизменной.

На рис. 5.4 показано изменение токов в обмотке электромагнита при неизменном установившемся токе. Кривые показывают, что в данном случае чем больше постоянная времени, тем больше время трогания.

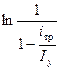
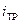
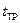
В заключение отметим, что при прочих равных усло­виях увеличение натяжения противодействующей пру­жины ведет к росту при этом также увеличивается.

Время отпускания электромагнита состоит из времени спадания потока до потока отпускания, при котором сила электро­магнита становится равной противодействующей силе и времени движения при отпускании.
В большинстве случаев время спада потока при отсутствии короткозамкнутых обмоток значительно меньше, чем время движения яко­ря при отпадании.
Поэтому в основном считаются со временем движения. Для упрощения расчетов можно принять, что якорь и подвижные части двигаются рав­ноускоренно под действием силы, равной средней силе пружины. Тогда время отпускания можно найти с по­мощью формулы

, (5.17)

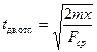
где т — приведенная к центру полюса масса якоря и подвижных частей; х— перемещение якоря; F_cp — приве­денное к центру полюса среднее значение силы отклю­чающей пружины на пути х.

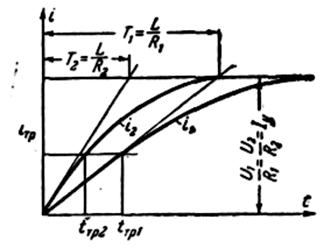Рис.5.5. Изменение токов в обмотке электромагнита при неизменном установившемся токе

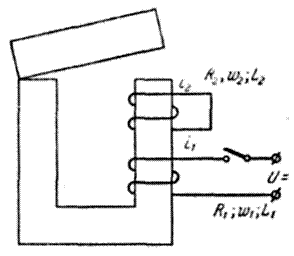
При включении питающей обмотки в магнитной цепи

нарастает поток. Этот поток наводит в короткозамкнутой обмотке э. д. с. Последняя вызывает ток такого направ­ления, при котором поток короткозамкнутой обмотки на­правлен встречно с намагничивающим. Результирующий поток равен разности этих потоков. Скорость нарастания потока уменьшается, а время трогания увеличива­ется.

Результирующий поток нарастает во времени по экс­поненте с суммарной постоянной времени

, (5.18)

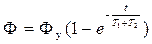
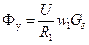
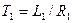
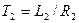
где установившийся поток;

, и — постоянные времени обмоток.

Рис. 5.5.Электромагнит с короткозамкнутой об­моткой

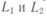
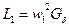
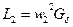
Если пренебречь потоками рассеяния, то индуктивности согласно равны:

; (5.19)

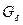
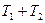
Ввиду того, что при отпущенном якоре мало, сум­марная постоянная времени невелика и замедле­ние электромагнита получается небольшим.

При отключении электромагнитас короткозамкнутой обмоткой можно считать, что ток в первичной обмотке практически мгновенно спадает до нуля из-за быстрого нарастания сопротивления дугового промежутка в от­ключающем аппарате.

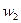
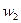
Изменение потока опре­деляется процессом затуха­ния тока в короткозамкнутой обмотке. При спадании потока в короткозамкнутой обмотке наводится э. д. с. и возникает ток, направлен­ный так, что поток, созда­ваемый обмоткой , пре­пятствует изменению (уменьшению) потока в системе.

Замедленное спадание потока создает выдержку време­ни при отпускании.

Для вторичной короткозамкнутой обмотки ненасы­щенной системы в этом случае можно записать:

. (5.20)

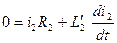
Поскольку величина зазора уменьшилась, индуктивность при притянутом якоре 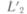больше, чем при отпущенном L-i.

Решив относительно тока, получим:

. (5.21)

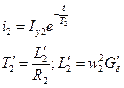
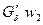
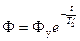
Умножив обе части на , после преобразова­ния получим:

. (5.22)

Благодаря тому, что рабочий зазор в притянутом состоя­нии в десятки и даже сотни раз меньше, чем в отпущен­ном 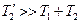можно получить время трогания при отпускании до 10 сек, тогда как время трогания при при­тяжении составляет доли секунды.

При н. с, равной нулю, в цепи устанавливается по­ток, определяемый кривой размагничивания материала и воздушным зазором. Этот остаточный поток может создавать силу притяжения большую, чем сила, развиваемая пружиной. Произойдет залипание якоря. Для устранения залипания ставится немагнитная про­кладка, снижающая величину остаточного потока.

В реальных конструкциях реле времени магнитная система при притянутом положении якоря сильно насы­щена.

Для насыщенной цепи справедливо уравнение

. (5.23)

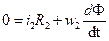
Решив уравнение относительно времени, получим:

, (5.24)

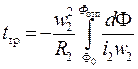
где 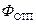–поток, при котором сила, развиваемая пружиной, равна силе электромагнита.

Для определения значения интеграла рассчитывается зависимость потока в рабочем зазоре от н. с. После это­го строится зависимость 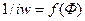и графическим ин­тегрированием решается.

в) Динамика электромагнитов переменного тока. Рассмотрим магнитную цепь электромагнита, у которо­го магнитопровод ненасыщен. Пусть включение проис­ходит в нуль напряжения. В этом случае можно запи­сать:

. (5.25)

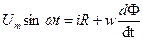
Поскольку цепь линейна, ток можно выразить через по­ток

.

. (5.26)

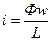
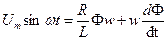
Решив это уравнение относительно потока, найдем:

, (5.27)

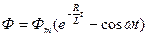
где Ф_т — максимальное значение потока.

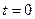
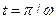
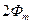
Согласно (5.27) при поток в системе также ра­вен нулю. Через время поток достигает наиболь­шего значения, поскольку постоянная составляющая по­тока складывается с переменной составляющей. Если пренебречь затуханием, то через полпериода поток до­стигает величины, равной .

По мере затухания постоянной составляющей потока пиковое значение потока будет уменьшаться, пока не до­стигнет . Таким образом, в электромагните перемен­ного тока наибольшие пиковые значения потока, а сле­довательно, и силы, будут иметь место в начале процес­са включения, причем пиковое значение потока и силы наступает примерно через 0,01 сек после начала включе­ния (при частоте тока 50 Гц. Это обеспечивает малое время трогания.

Если магнитная система насыщена, то возникновение постоянной составляющей потока в момент включения ведет к появлению большого сильно искаженного намаг­ничивающего тока.

При включении в нуль тока (потока) постоянная со­ставляющая не появляется и пиковое значение потока появляется через четверть периода после начала вклю­чения. Таким образом, и в этом случае обеспечивается быстрое срабатывание электромагнита без применения специальных мер.

Расчет динамических характеристик электромагнитов переменного тока аналитически очень затруднен. Эту за­дачу удается решить применением аналоговых счетных машин. Необходимо отметить, что в момент вклю­чения электромагнита рабочий зазор в магнитной цепи велик, что вызывает согласно большой намагни­чивающий ток, в десятки раз больший, чем ток в притя­нутом положении якоря.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник