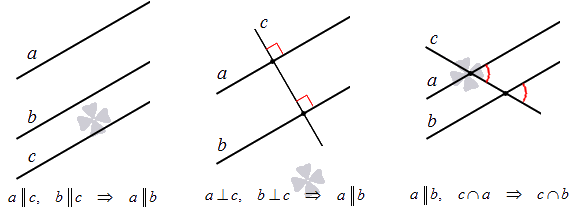Что такое все возможные обозначения прямой
Прямая на плоскости – необходимые сведения
Статья рассказывает о понятии прямой на плоскости. Рассмотрим основные термины и их обозначения. Поработаем со взаимным расположением прямой и точки и двух прямых на плоскости. Поговорим об аксиомах. В итоге обсудим методы и способы задания прямой на плоскости.
Прямая на плоскости – понятие
Для начала необходимо иметь четкое представление о том, что такое плоскость. Любую поверхность чего-либо можно отнести к плоскости, только от предметов она отличается своей безграничностью. Если представить, что плоскость – это стол, то в нашем случае он не будет иметь границ, а будет бесконечно огромен.
Если карандашом дотронуться до стола, останется отметина, которую можно называть «точкой». Таким образом, получим представление о точке на плоскости.
Рассмотрим понятие прямой линии на плоскости. Если провести прямую на листе, то она отобразится на нем с ограниченной длиной. Мы получили не всю прямую, а только ее часть, так как на самом деле она не имеет конца, как и плоскость. Поэтому изображение прямых и плоскостей в тетради формальное.
Взаимное расположение прямой и точки
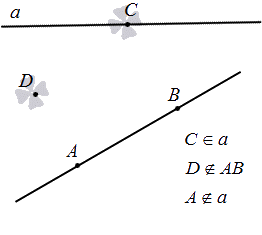
На каждой прямой и в каждой плоскости могут быть отмечены точки.
Для точки и прямой известны только два варианта расположения: точка на прямой, иначе говоря, что прямая проходит через нее, или точка не на прямой, то есть прямая не проходит через нее.
Через любые две точки, находящиеся в любых плоскостях, существует единственная прямая, которая проходит через них.
Прямая, расположенная на плоскости, имеет большое количество точек. Отсюда исходит аксиома:
Если две точки прямой лежат в плоскости, то и все остальные точки данной прямой принадлежат плоскости.
Множество точек, находящееся между двумя заданными, называют отрезком прямой. Он имеет начало и конец. Введено обозначение двумя буквами.
Точка делит прямую на две части, называемые лучами. Имеем аксиому:
Взаимное расположение прямых на плоскости
Расположение прямых на плоскости может принимать вид двух состояний.
Две прямые на плоскости могут совпадать.
Такая возможность появляется, когда прямые имеют общие точки. Исходя из аксиомы, написанной выше, имеем, что через две точки проходит прямая и только одна. Значит, что при прохождении 2 прямых через заданные 2 точки, они совпадают.
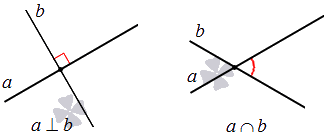
Две прямые на плоскости могут пересекаться.
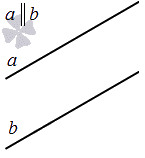
Две прямые на плоскости могут быть параллельны.
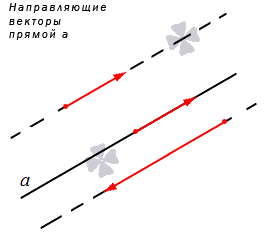
Прямая на плоскости рассматривается вместе с векторами. Особое значение придается нулевым векторам, которые лежат на данной прямой или на любой из параллельных прямых, имеют название направляющие векторы прямой. Рассмотрим рисунок, расположенный ниже.
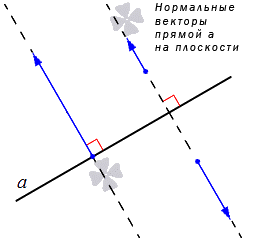
Ненулевые векторы, расположенные на прямых, перпендикулярных данной, иначе называют нормальными векторами прямой. Подробно имеется описание в статье нормальный вектор прямой на плоскости. Рассмотрим рисунок ниже.
Если на плоскости даны 3 линии, их расположение может быть самое разное. Есть несколько вариантов их расположения: пересечение всех, параллельность или наличие разных точек пересечения. На рисунке показано перпендикулярное пересечение двух прямых относительно одной.
Для этого приводим необходимы факторы, доказывающие их взаимное расположение:
Рассмотрим это на рисунках.
Способы задания прямой на плоскости
Прямая на плоскости может быть задана несколькими способами. Все зависит от условия задачи и на чем будет основано ее решение. Эти знания способны помочь для практического расположения прямых.
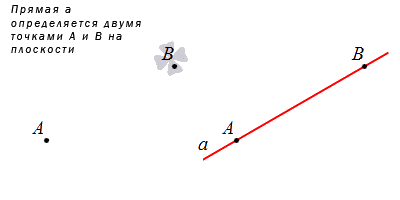
Прямая задается при помощи указанных двух точек, расположенных в плоскости.
Из рассмотренной аксиомы следует, что через две точки можно провести прямую и притом только одну единственную. Когда прямоугольная система координат указывает координаты двух несовпадающих точек, тогда можно зафиксировать уравнение прямой, проходящей через две заданные точки. Рассмотрим рисунок, где имеем прямую, проходящую через две точки.
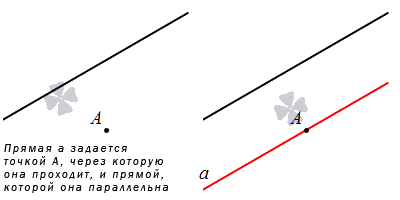
Прямая может быть задана через точку и прямую, которой она параллельна.
Данный способ имеет место на существование, так как через точку можно провести прямую, параллельную заданной, причем, только одну. Доказательство известно еще из школьного курса по геометрии.
Если прямая задана относительно декартовой системы координат, тогда возможно составление уравнения прямой, проходящей через заданную точку параллельно заданной прямой. Рассмотрим принцип задания прямой на плоскости.
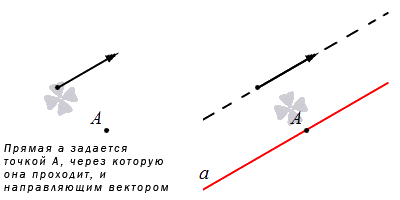
Прямая задается через указанную точку и направляющий вектор.
Когда прямая задается в прямоугольной системе координат, есть возможность составления канонического и параметрического уравнений на плоскости. Рассмотрим на рисунке расположение прямой при наличии направляющего вектора.
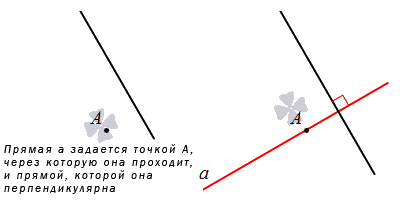
Четвертым пунктом задания прямой имеет смысл, когда указана точка, через которую ее следует начертить, и прямая, перпендикулярная ей. Из аксиомы имеем:
Через заданную точку, расположенную на плоскости, пройдет только одна прямая, перпендикулярная заданной.
И последний пункт, относящийся к заданию прямой на плоскости, это при указанной точке, через которую проходит прямая, и при наличии нормального вектора прямой. При известных координатах точки, которая расположена на заданной прямой, и координатах нормального вектора есть возможность записывания общего уравнения прямой.
Мерзляк 5 класс — § 4. Плоскость. Прямая. Луч
Вопросы к параграфу
1. Является ли плоскость бесконечной? — Да, плоскость бесконечна, её можно продолжать во все стороны без ограничения.
2. Имеет ли прямая концы? — Нет, прямая не имеет концов, она бесконечна, продолжать прямую можно без ограничений.
3. Сколько прямых проходит через две точки? — Через две точки можно провести только одну единственную прямую.
4. Как обозначают прямую? — Прямую можно обозначать двумя способами: либо одной строчной латинской буквой (a, b, c и т.д.), либо двумя прописными латинскими буквами, обозначающими точки, лежащие на этой прямой (AB, DC, RK и т.д.).
5. Как называют части прямой, на которые её делит любая точка этой прямой? Как при этом называют эту точку? — Часть прямой вместе с точкой, от которой начинается эта часть прямой, называется лучом. Точку, делящую прямую на 2 части называют началом луча.
6. Как обозначают луч? — Луч обозначают двумя прописными латинскими буквами: буквой, обозначающей точку начала луча и буквой, обозначающую любую точку лежащую на этом луче.
7. С какими геометрическими фигурами вы познакомились в этом параграфе? — Прямая и луч.
Решаем устно
1. Вычислите:
1) 312 • 10 = 3 120
2) 5 • 1 000 = 5 000
3) 100 • 10 000 = 1 000 000
4) 720 : 9 = 80
5) 480 : 4 = 120
6) 480 : 16 = 30
7) 1 212 : 12 = 101
8) 1 010 : 5 = 202
9) 1 515 : 15 = 101
2) Реши:
Удвойте число 26. 26 • 2 = 52
Найдите половину числа 26. 26: 2 = 13
Утройте число 27. 27 • 3 = 81
Найдите треть числа 27. 27 : 3 = 9
3. Около школы растут берёзы и тополя, причём берёз восемь, а тополей — на 16 больше. Сколько всего деревьев растёт около школы? Во сколько раз берёз меньше, чем тополей?
1) 8 + 16 = 24 (дерева) — тополя.
2) 8 + 24 = 32 (дерева) — растёт около школы всего.
3) 24 : 8 = 3 (раза) — берёз меньше, чем тополей.
Ответ: 32 дерева всего, берёз в 3 раза меньше, чем тополей.
4. В 10 ч утра со станции отправился поезд со скоростью 60 км/ч. На каком расстоянии от станции будет поезд в 15 ч того же дня, если будет двигаться с этой же скоростью и без остановок?
1) 15 — 10 = 5 (часов) — проедет поезд за указанное время.
2) 60 • 5 = 300 (км) — проедет поезд за 5 часов.
Ответ: Поезд будет на расстоянии 300 км от станции.
5. Таня и Миша учатся в одной школе. Таня живёт в доме около одной конечной остановки автобуса, а Миша — в доме около другой конечной остановки этого же маршрута. Когда они едут в школу, то Таня выходит на пятой остановке, а Миша — на седьмой. Сколько всего остановок на этом маршруте?
1 (начальная остановка Тани) + 5 (остановки которые проезжает Таня) + 6 (остановки которые проезжает Миша — остановка школы, так как мы её уже посчитали в Танином маршруте) + 1 (начальная остановка Миши) = 1 + 5 + 6 + 1 = 13.
Ответ: на этом маршруте всего 13 остановок (включая конечные).
6) Верёвку разрезали на три куска так, что первый кусок оказался на 3 м короче второго и на 3 м длиннее третьего куска. На сколько метров третий кусок короче второго?
3 + 3 = 6 (метров) — третий кусок короче второго.
Ответ: на 6 метров третий кусок короче второго.
Упражнения
85. Отметьте в тетради точки М и К и проведите через них прямую. Отметьте на отрезке МК точку N. Принадлежит ли точка N прямой МК? Отметьте на прямой МК точку Р, лежащую вне отрезка МК. Запишите все возможные обозначения этой прямой.
Точка N принадлежит прямой MK.
Возможные обозначения этой прямой: PM, PN, PK, MN, MK, NK, KN, KM, KP, NM, NP, MP.
86. Проведите произвольную прямую и отметьте на ней точки А, В и С. Запишите все возможные обозначения этой прямой.
Возможные обозначения этой прямой: AB, AC, BC, CB, CA, BA.
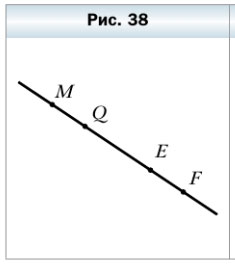
87. Рассмотрите рисунок 38.
Верно ли утверждение:
1) точка Q принадлежит отрезку ME — утверждение верно.
2) точка Q принадлежит лучу EF — утверждение неверно.
3) точка Q принадлежит лучу FE — утверждение верно.
4) точка Е принадлежит лучу MF и лучу FM — утверждение верно.
5) точка М принадлежит отрезку QE — утверждение неверно.
6) точка М принадлежит прямой QE — утверждение верно.
88. Пересекаются ли изображённые на рисунке 39:
1) прямая СЕ и отрезок АВ — да, пересекаются, так как прямую СЕ можно продолжить в обе стороны бесконечно долго.
2) луч ОК и прямая СЕ — да, пересекаются, так как луч ОК может быть продолжен в сторону прямой СЕ бесконечно долго.
3) луч ОК и отрезок АВ — нет, не пересекаются, так как отрезок АВ не может быть продолжен, а при продолжении луча ОК далее точки К не приведёт к пересечению лучом заданного отрезка.
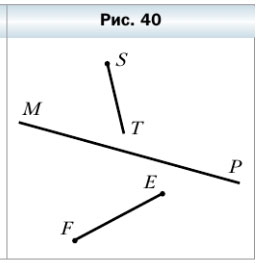
89. Пересекаются ли изображённые на рисунке 40:
1) прямая МР и отрезок EF — нет, так как отрезок EF продолжить нельзя, а продолжение прямой в любую из сторон не приведёт к пересечению этих геометрических фигур.
2) луч ST и прямая МР — да, так как луч ST может быть продолжен в сторону прямой бесконечно долго.
3) отрезок EF и луч ST — да, так как луч ST может быть продолжен в сторону отрезка EF бесконечно долго.
90. Отметьте в тетради:
1) четыре точки, из которых никакие три не лежат на одной прямой
2) пять точек, из которых никакие три не лежат на одной прямой
91. На прямой АВ отмечены две точки М и N. Назовите фигуры, которые при этом образовались.
92. Запишите все отрезки, прямые и лучи, изображённые на рисунке 41.
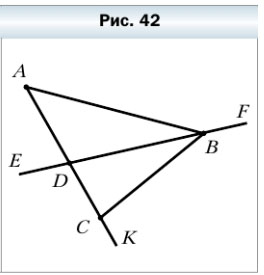
93. Запишите все отрезки, прямые и лучи, изображённые на рисунке 42.
94. Начертите два луча так, чтобы их общая часть была:
1) точкой
Общей частью лучей OS и OT является их начальная точка O.
2) отрезком
Общей частью лучей KP и NM является отрезок KN.
3) лучом
Общей частью лучей AC и BC является луч BC.
95. Отметьте на плоскости точки М, К, Т и F так, чтобы луч МК пересекал прямую TF, а луч TF не пересекал прямую МК.
96. Начертите прямую АС, отрезки КЕ и BD, луч ST так, чтобы отрезок КЕ пересекал прямую АС и не пересекал луч ST, отрезок BD не пересекал прямую АС и отрезок КЕ и пересекал луч ST, а прямая АС и луч ST пересекались.
97. Начертите луч CD, прямую АВ и отрезки МК и ОР так, чтобы отрезок МК лежал на прямой АВ, отрезок ОР — на луче CD и чтобы прямая АВ пересекала отрезок ОР, а луч CD — отрезок МК.
98. Сколько лучей образуется, если на прямой отметить: 1) четыре точки; 2) 100 точек?
Каждая точка делит прямую на 2 части — на 2 луча. Значит:
Обозначить образовавшиеся лучи можно множеством способов.
99. Точки А, В и С лежат на одной прямой. Найдите длину отрезка ВС, если АВ = 24 см, АС = 32 см. Сколько решений имеет задача?
Задача имеет 2 решения.
Решение 1 — точка В лежит между точками А и С
32 — 24 = 8 (см) — длина отрезка ВС
Решение 2 — точка А лежит между точками С и В
32 + 24 = 56 (см) — длина отрезка ВС
100. Точки М, К и N лежат на одной прямой. Найдите длину отрезка KN, если МК = 15 см, MN = 6 см.
Задача имеет 2 решения.
Решение 1 — точка N лежит между точками К и М
15 — 6 = 9 (см) — длина отрезка КN
Решение 2 — точка М лежит между точками К и N
15 + 6 = 21 (см) — длина отрезка КN
101. На плоскости проведено пять попарно пересекающихся прямых. Каким может оказаться наименьшее количество точек пересечения этих прямых? Наибольшее количество?
Наименьшее количество точек пересечения пяти попарно пересекающихся прямых — одна:
Наибольшее количество точек пересечения пяти попарно пересекающихся прямых — десять:
Ответ: 1 точка, 10 точек.
102. На плоскости проведены три прямые. Каким может оказаться наибольшее количество частей, на которые эти прямые разбили плоскость, и каким — наименьшее?
Наибольшее количество частей плоскости получится в случае, если прямые попарно пересекаются между собой в максимальном количестве точек. Для трёх прямых это три точки пересечения. В результате плоскость будет разбита на 7 частей.
Минимальное количество частей плоскости получится в случае, если прямые не пересекаются вовсе, то есть они параллельны друг другу. В результате плоскость будет разбита на 4 части.
Ответ: 7 частей, 4 части.
103. Проведите шесть прямых и отметьте на них 11 точек так, чтобы на каждой прямой было отмечено ровно четыре точки.
104. На плоскости проведены три прямые. На одной прямой отмечено пять точек, на второй — семь точек, а на третьей — три точки. Какое наименьшее количество различных точек может оказаться отмеченным?
Наименьшее количество отмеченных точек — 12.
Упражнения для повторения
105. В парке растёт 168 дубов, берёз — в 4 раза меньше, чем дубов, а клёнов — на 37 деревьев больше, чем берёз. Сколько всего дубов, берёз и клёнов растёт в парке?
1) 168 : 4 = 42 (дерева) — берёзы.
2) 42 + 37 = 79 (деревьев) — клёны.
3) 168 + 42 + 79 = 289 (деревьев) — всего в парке.
Ответ: 289 деревьев.
106. Группа туристов прошла пешком 72 км, проехала на поезде расстояние в 5 раз большее, чем прошла пешком, а на автобусе проехала на 128 км меньше, чем на поезде. Сколько всего километров прошли и проехали туристы?
1) 72 • 5 = 360 (км) — проехали на поезде.
2) 360 — 128 = 232 (км) — проехали на автобусе.
3) 72 + 360 + 232 = 664 (км) — прошли и проехали всего.
107. Отправившись в гости к Змею Горынычу, Баба-яга пролетела в своей ступе 276 км за 4 ч, а остальные 156 км прошла за 6 ч в сапогах-скороходах. На сколько скорость движения ступы больше, чем скорость движения сапог-скороходов?
1) 276 : 4 = 69 (км/ч) — скорость движения ступы.
2) 156 : 6 = 26 (км/ч) — скорость движения сапог-скороходов.
3) 69 — 26 = 43 (км/ч) — скорость движения ступы больше, чем скорость движения сапог-скороходов.
108. По течению реки лодка проплывает 95 км за 5 ч, а против течения — 119 км за 7 ч. На сколько скорость движения лодки против течения меньше её скорости движения по течению?
1) 95 : 5 = 19 (км/ч) — скорость движения лодки по течению реки.
2) 119 : 7 = 17 (км/ч) — скорость движения лодки против течения.
3) 19 — 17 = 2 (км/ч) — скорость движения лодки против течения лодки меньше, чем скорость движения лодки по течению.
109. На прямой отметили 20 точек так, что расстояние между любыми двумя соседними точками равно 4 см. Найдите расстояние между крайними точками.
Между 20 точками будет 19 промежутков.
4 • 19 = 76 (см) — расстояние между крайними точками.
110. На прямой отметили точки так, что расстояние между любыми двумя соседними точками равно 5 см, а между крайними точками — 45 см. Сколько точек отмечено на прямой?
45 : 5 = 9 (шт) — промежутков по 5 см каждый.
Для того, чтобы образовалось 9 промежутков надо отметить 10 точек.
Задача от мудрой совы
111. Как расставить 16 учеников в три ряда, чтобы в каждом ряду их было поровну?
Это значит, что либо один человек должен стоять сразу во всех трёх рядах, либо два ученика должны стоять сразу в двух рядах каждый. Сделать это можно следующими (и подобными им) способами:
Прямая

Всего получено оценок: 147.
Всего получено оценок: 147.
В геометрии любой объект состоит из базовых элементов: точек, прямых и плоскостей. Любая фигура, не важно, плоская она или объемная, будет состоять из этих элементов. Определение точки понятно, но вот как понять, что такое прямая и как она может быть бесконечной – в 5 классе не так просто разобраться.
Определение прямой
Определение прямой начинается с определения линии. Что такое линия? Это множество точек, соединенных между собой. Линия может быть прямой, кривой, ломанной, непрерывной и даже разомкнутой. И именно из-за этого разнообразия линии очень трудно определить в пространстве. Непонятно, как пройдет та или иная кривая, когда выйдет за пределы листа. Поэтому был выделен отдельный вид линий – прямые.
Когда в разговоре вы слышите прямая – люди имеют в виду прямую линию, но последнее слово в словосочетании принято опускать.
Что такое прямая в математике? Прямые это бесконечные непрерывные линии, которые не имеют искривлений. Первое правило линий: через любые две точки можно провести линию. А вот через три точки уже не всегда. Чаще всего через три точки можно провести три прямых.
Если прямая проходит через три точки, то про эти точки говорят, что они лежат на одной прямой. Прямые, как правило, обозначают малой латинской буквой или по названию двух точек на прямой.
Почему двух, а не трех? Очень просто: через две точки может пройти только одна прямая. Тогда как через одну: бесконечное множество. А три точки не имеет смысла использовать: ни к чему усложнять обозначение.
Взаимное расположение прямых
Две прямые в пространстве могут располагаться по-разному. Самый простой и частый случай это пересечение. Если две прямые имеют одну общую точку, про такие прямые говорят, что они пересекаются.
А как прямые назвать, если они не пересекаются? Тогда – параллельные, то есть прямые, которые не имеют общих точек.
А что будет, если у двух прямых две и больше общих точек? Тогда прямые совпадут.
При пересечении двух прямых образуется две пар вертикальных углов. Вертикальные углы в каждой паре равны между собой.
Если угол пересечения равен 90 градусов, то прямые перпендикулярны друг другу.

Точка на прямой
Точка на прямой это почти магия. Сама по себе прямая это множество точек, но стоит отметить одну из них и геометрическую фигуру можно назвать как прямой, так и двумя лучами с началом в одной точке. Если поставить две точки на прямой, то они будут отделять часть прямой, которую называют отрезком.
Любой отрезок является частью прямой.
Что мы узнали?
Мы дали определении линиям, выделили виды линий, а так же рассмотрели, какая из линий может называться прямой. Поговорили о том, как обозначаются прямые и как они могут располагаться в пространстве относительно друг друга. Выяснили, что точка на прямой может сделать из прямой отрезок или луч.