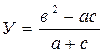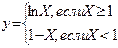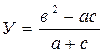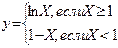Что такое вычислительные алгоритмы
ВЫЧИСЛИТЕЛЬНЫЙ АЛГОРИТМ
Машинная команда есть машинное слово, к-рое содержит информацию об операции, напр. арифметической, и ее оперантах (объектах, над к-рыми производится операция, и результате операции). Арифметич. операция над парой машинных чисел может вывести результат из совокупности М по двум причинам: вследствие превышения допустимого числа значащих цифр; вследствие превышения допустимой величины машинного числа. В первом случае применяется операция округления, к-рая возвращает результат действия в множество М, но делает само действие приближенным и приводит к потере точности. Второй случай приводит к аварийной остановке ЭВМ (АВОСТ, или «аварийный останов»).
Композиция арифметич. операции, примененной к паре машинных чисел, и операции округления называется квази операцией. Множество М вместе с определенной над ним совокупностью квазиопераций образует замкнутую систему N, однако, в отличие от поля действительных чисел, N не образует поля. Система N зависит от выбора ЭВМ.
Реальный В. а. складывается из двух частей:
а) абстрактного (или собственно) В. а., к-рый применяется к математич. объектам (элементам конечномерных векторных пространств, полей, алгебраич. систем, функциональных пространств и т. д.), не связан с конкретной ЭВМ и может записываться в общепринятых математич. терминах или на каком-либо алгоритмич. языке;
б) программы, т. е. совокупности машинных команд, описывающих В. а., к-рая организует реализацию вычислительного процесса в конкретной ЭВМ.
Первая часть В. а. является исходной и переходит во вторую часть с помощью различных методов программирования. В. а. содержит ряд управляющих параметров, к-рые остаются неопределенными в первой части и фиксируются в программе, полностью определяя вычислительный процесс, обеспечивая адаптацию его первой части к конкретной ЭВМ.
В. а. осуществляет переработку числовой и символьной информации и, как правило, связан с потерей информации и точности. Потеря точности является следствием ряда погрешностей, появляющихся на различных этапах вычислений: погрешности модели, аппроксимации, входных данных, округления. Погрешность модели является следствием приближенности математич. описания реального процесса. Погрешность входных данных зависит от ошибок наблюдения, измерения и т. п., но также может включать в себя и ошибку округления входной информации. Иногда погрешность модели и погрешность входных данных объединяют одним названием неустранимая погрешность. Погрешность аппроксимации возникает, если рассматривать абстрактный В. а. как нек-рую дискретную модель, к-рая, как правило, аппроксимирует континуальную модель. В нек-рых случаях абстрактный В. а. является самостоятельной дискретной моделью, к-рая не сопоставляется ни с какой другой моделью; в этом случае нет смысла говорить о погрешности аппроксимации. Погрешности округления могут встречаться только в реальном вычислительном процессе и зависят от выбора ЭВМ. При заданных входных данных и абстрактном В. а. промежуточные и выходные данные, получаемые в ЭВМ, зависят от выбора ЭВМ и режима ее работы (вычисления с одинарной и двойной точностью). Абстрактный В. а. допускает эквивалентные преобразования, к-рые при заданных входных данных могут менять промежуточные данные, но оставляют неизменным окончательный результат. В. а., соответствующий двум различным эквивалентным представлениям абстрактного В. а., может при фиксированной ЭВМ и входных данных приводить к различным окончательным результатам.
Помимо свойства точности, В. а. должен обладать свойством устойчивости. Устойчивость В. а. определяется как свойство В. а., позволяющее судить о скорости накопления суммарной вычислительной погрешности. Имеется градация устойчивости (соответственно неустойчивости), основанная на измерении исходной ошибки округления и суммарной вычислительной погрешности в различных нормах. В тех случаях, когда В. а. сводится к последовательности линейных рекуррентных соотношений, устойчивость В. а. определяется в терминах норм конечномерных матриц в конечномерных векторных пространствах. Свойство устойчивости определяется как структурой абстрактного В. а., так и влиянием ошибок округления. Так, устойчивость итерационного процесса x n+1 = Аnx n + bn, где матрица Аn также вычисляется, будет зависеть от влияния ошибок округления в коэффициентах матрицы на ее норму. Ошибки округления, входя в коэффициенты различных уравнений и операторов, вносят возмущения в математич. модель абстрактного В. а. и в этом смысле могут интерпретироваться так же, как и ошибки модели. Чем лучше свойства устойчивости абстрактного В. а., тем меньше, при заданном абстрактном В. а., результаты вычислений зависят от выбора ЭВМ и эквивалентных представлений абстрактного В. а.
Другим условием, особенно важным в массовых вычислениях, является экономичность В. а., измеряемая затратой машинного времени, необходимой для достижения заданной точности вычисления. Экономичные В. а. получили широкое распространение в задачах математич. физики (см., напр., дробных шагов метод). Важной задачей теории В. а. является оптимизация В. а.
При построении В. а. характерна тенденция к контролю точности. Контроль точности может косвенно осуществляться за счет увеличения устойчивости и порядка аппроксимации В. а., изменения параметров В. а. (внутренняя сходимость), сравнения двух численных решений одной и той же задачи, соответствующих различным В. а., применения тестов и т. д. Прямой контроль точности осуществляется в том случае, когда удается полупить двусторонние оценки (или, по крайней мере, односторонние оценки) результата вычислений. Теоретич. оценки такого рода не всегда возможны и эффективны, т. к. не всегда дают достаточно точные границы отклонения численного решения от точного. Получил распространение интервальный анализ, к-рый дает возможность в процессе вычислений строить доверительные границы для вычисляемых величин.
Различия в результатах абстрактного и реального В. а. определяются довольно сложными связями между их параметрами. Так, в абстрактном В. а. для сходящегося итерационного процесса точность ε, вообще говоря, тем больше, нем больше число итераций n. В случае реального В. а. эта ситуация может измениться вследствие влияния ошибок округления и, начиная с нек-рого момента, разность между n-й итерацией и тонным решением может потерять тенденцию к убыванию.
Вообще говоря, абстрактный В. а. строится независимо от выбора конкретной ЭВМ и только косвенно упитывает ее конфигурацию своими свойствами аппроксимации и устойчивости. Так, для машин с большим быстродействием, но при малой оперативной памяти при решении дифференциальных уравнений с частными производными целесообразно применение экономичных абсолютно устойчивых схем высокой точности. В связи с появлением ЭВМ с параллельно действующими процессорами полупили развитие параллельные алгоритмы и параллельное программирование. Сущность параллельного программирования заключается в разбиении перерабатываемых численных массивов на пасти (подмассивы), независимо перерабатываемые соответствующими процессорами; производится обмен информацией между подмассивами, причем время, затрачиваемое на этот обмен, существенно меньше, нем выигрыш времени, достигаемый в результате распараллеливания спета. Это делает эффективным применение ЭВМ с параллельным действием, позволяя достигать резкого увеличения быстродействия, особенно при решении больших задач.
Многообразие ЭВМ приводит к многообразию программ, реализующих один и тот же абстрактный В. а. Составление программ является трудоемким процессом, и поэтому особое значение приобретает проблема адаптации, т. е. быстрого и по возможности автоматич. преобразования (при заданном абстрактном В. а.) программы с одной ЭВМ на другую (см. Программирование).
Алгоритм
Из Википедии — свободной энциклопедии
Алгори́тм (лат. algorithmi — от имени среднеазиатского математика Аль-Хорезми [1] ) — конечная совокупность точно заданных правил решения некоторого класса задач или набор инструкций, описывающих порядок действий исполнителя для решения определённой задачи. В старой трактовке вместо слова «порядок» использовалось слово «последовательность», но по мере развития параллельности в работе компьютеров слово «последовательность» стали заменять более общим словом «порядок». Независимые инструкции могут выполняться в произвольном порядке, параллельно, если это позволяют используемые исполнители.
Ранее в русском языке писали «алгорифм», сейчас такое написание используется редко, но тем не менее имеет место исключение (нормальный алгорифм Маркова).
Часто в качестве исполнителя выступает компьютер, но понятие алгоритма необязательно относится к компьютерным программам, так, например, чётко описанный рецепт приготовления блюда также является алгоритмом, в таком случае исполнителем является человек (а может быть и некоторый механизм, например ткацкий или токарный станок с числовым управлением, и пр.).
Можно выделить алгоритмы вычислительные (далее речь в основном идёт о них), и управляющие. Вычислительные, по сути, преобразуют некоторые начальные данные в выходные, реализуя вычисление некоторой функции. Семантика управляющих алгоритмов существенным образом может отличаться и сводиться к выдаче необходимых управляющих воздействий либо в заданные моменты времени, либо в качестве реакции на внешние события (в этом случае, в отличие от вычислительного алгоритма, управляющий может оставаться корректным при бесконечном выполнении).
Понятие алгоритма относится к первоначальным, основным, базисным понятиям математики. Вычислительные процессы алгоритмического характера (арифметические действия над целыми числами, нахождение наибольшего общего делителя двух чисел и т. д.) известны человечеству с глубокой древности. Однако в явном виде понятие алгоритма сформировалось лишь в начале XX века.
Частичная формализация понятия алгоритма началась с попыток решения проблемы разрешения (нем. Entscheidungsproblem ), которую сформулировал Давид Гильберт в 1928 году. Следующие этапы формализации были необходимы для определения эффективных вычислений [2] или «эффективного метода» [3] ; среди таких формализаций — рекурсивные функции Геделя — Эрбрана — Клини 1930, 1934 и 1935 гг., λ-исчисление Алонзо Чёрча 1936 г., «Формулировка 1» Эмиля Поста 1936 года и машина Тьюринга.
Основные вычислительные алгоритмы.
Алгоритмические (или вычислительные) процессы обработки данных делятся на виды:
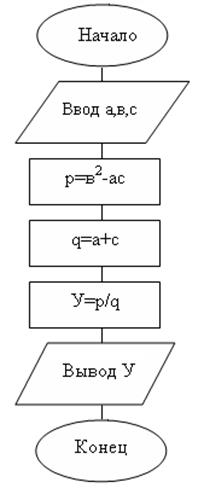
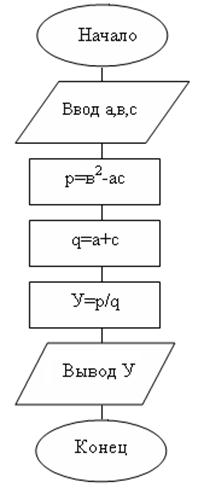
Линейным называется такой вычислительный процесс, в котором самостоятельные этапы вычислений выполняются в последовательности их записи, т.е. в естественном порядке.
Каждая операция является самостоятельной, независимой от каких-либо условий.
Линейные вычислительные процессы имеют место при вычислении арифметических выражений.
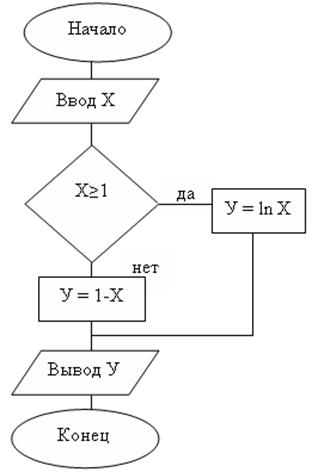
Ветвящимсяназывается такой процесс, в котором его реализация происходит по одному из нескольких заранее предусмотренных (возможных) направлений в зависимости от исходных условий или промежуточных результатов. Каждое отдельное направление вычислений в таком процессе называется ветвью вычисления. Выбор осуществляется проверкой выполнения логического условия.
В каждом конкретном случае обработки данных вычислительный процесс выполняется лишь по одной ветви, а выполнение остальных – исключается.
Ветвящийся процесс, включающий в себя две ветви, называется простым, более двух ветвей- сложным. Сложный ветвящийся процесс можно представить с помощью простых ветвящихся процессов.
Любая ветвь, по которой осуществляются вычисления, должна приводить к завершению вычислительного процесса.
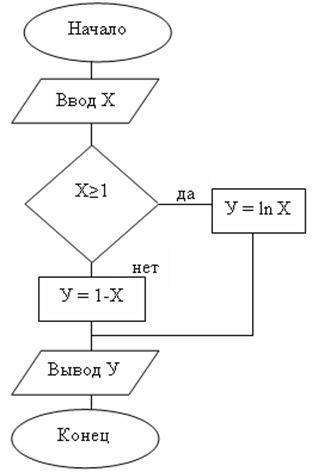
При реализации алгоритмов многих задач наблюдается многократное повторение отдельных этапов их вычислительного процесса. Такие многократно повторяемые этапы вычислений называются циклами, а вычислительные процессы, содержащие многократно повторяемые этапы называются циклическими.
II Алгоритмы и параллелизм (часть первая)
В данном разделе будут рассмотрены: понятие алгоритма, вычислительная сложность алгоритма, а также особенности параллельных вычислений для классических задач.
Среди подходов к реализации параллелизма можно выделить три: ручной, автоматический и модельный. При «ручном проектировании» программист берет на себя всю ответственность за структуру и качество параллельного решения. Используя ту или иную библиотеку (MPI, OPEN МР и т.п.), он создает параллельную программу, самостоятельно формируя ее структуру, связи, синхронизацию и т.д. При автоматическом распараллеливании написанная в обычном стиле программа преобразуется в параллельную без участия программиста. Разумеется, за качество распараллеливания отвечает система или среда программирования. Хорошая программная система может появиться только тогда, когда разум вычислительной системы будет выше человеческого разума. В настоящее время приходится довольствоваться в основном распараллеливанием цикла. В полном объеме эта задача в настоящее время не решена. Модельный подход отличается тем, что в нем есть та или иная формальная основа – универсальная алгоритмическая модель параллельных вычислений.
Таким образом, на сегодня реальным является параллелизм универсальных вычислений и их использование в качестве основных модулей при решении конкретных задач.
Опыт программирования показывает, что точность вычислений часто зависит от их порядка, хотя математически эти операции могут быть выполнены в произвольном порядке. Так, даже для целых чисел результаты вычислений 3/2*6 и 3*6/2 будут разными, в случае чисел с плавающей точкой эти зависимости усиливаются.
Понятие алгоритма
Алгоритм – точное предписание, определяющее последовательность действий, обеспечивающую получение требуемого результата из исходных данных. Обращаем внимание на слова последовательность действий. Действительно, само понятие алгоритма и его использование практически всегда предполагали последовательные вычисления.
Для того чтобы понятие алгоритма применять для параллельных вычислений, используем определение Т. Кормена. Алгоритм – это формально описанная вычислительная процедура, получающая исходные данные (input), называемые также входом алгоритма или его аргументом, и выдающая результат вычислений на выход (output). Заметим, что здесь ничего не говорится о последовательности действий. В дальнейшем будем рассматривать алгоритм как «черный ящик», выполняющий преобразование входных данных в выходные, эти преобразования могут быть последовательными, параллельными или смешанными.
Основной характеристикой алгоритма является его вычислительная сложность.
Понятие вычислительной сложности алгоритма
Пусть А – алгоритм решения некоторого класса задач, например, сортировки. Назовем размерностью задачи \(n\) совокупность параметров (их количество), характеризующих объем обрабатываемых исходных данных и определяющих необходимые для выполнения расчетов ресурсы (время, память). Для задачи сортировки – это тип> Понятие алгоритма
Вычислительная сложность алгоритма зависит от размерности задачи и делится на:
Временная сложность определяет время, необходимое для выполнения заданного алгоритма. Пространственная (емкостная) сложность определяет необходимый объем памяти.
Здесь предполагается, что вычислительная сложность – это временная сложность. Если понятие вычислительной сложности будет предполагать использование пространственной сложности, будет оговорено.
Граф параллельного алгоритма
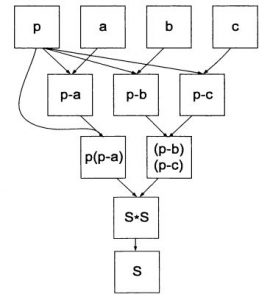
Рис. 2. Граф параллельного алгоритма вычисления площади треугольника
Данный граф является однонаправленным. Высота графа определяет минимальное число операций, за которые можно > Понятие вычислительной сложности алгоритма
Степень параллелизма для данного этапа – количество операций, которое можно выполнить параллельно.
Средняя степень параллелизма определяется как отношение общего числа операций, которые надо выполнить, на число этапов, за которые эти операции выполняются. Для нашего примера общее число операций равно 7, а число шагов равно 4, средняя степень параллелизма равна 1.75. В отличие от ускорения, эта характеристика никак не зависит от числа ядер процессора и характеризует только алгоритм.
Параллельные алгоритмы вычисления суммы
Пусть необходимо вычислить значение суммы:
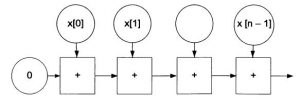
Рассмотрим фрагмент программы для вычисления суммы классическим последовательным способом:
Рис. 3. Граф для последовательного вычисления суммы
Очевидно, что, независимо от числа ядер, данный алгоритм требует последовательного выполнения n операций сложения и ср> Граф параллельного алгоритма
Каскадный метод вычисления суммы
Пусть есть бесконечное число вычислительных блоков (ядер). В этом случае для каждой пары слагаемых вычисляем сумму параллельно (предполагается, что все слагаемые предварительно вычислены и доступны вычислительному блоку):
Для \(n/2\) процессоров все элементы \(b[j]\) могут быть вычислены параллельно.
Далее, для полученых частичных сумм вычисляем сумму:
Программная реализация каскадного метода для последовательного режима:
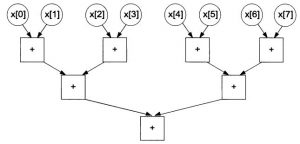
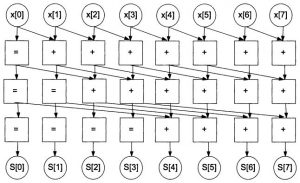
Так как сумма элементов с четным и нечетным номером может выполняться параллельно для всех пар, то в графе на первом шаге получим \(n/2\) вершин. Каждый очередной шаг приводит к уменьшению числа вершин в 2 раза. Граф для 8-ми слагаемых представлен на рис. 4.
Очевидно, что каскадный метод требует шагов при условии наличия \(n/2\) ядер процессора.
Определим степень параллелизма алгоритма:
Определим показатели ускорения, эффективности и стоимости для каскадного метода.
Заметим, что средняя степень параллелизма совпадает с ускорением при условии наличия максимального необходимого числа ядер. При \( n \rightarrow \infty\) эффективность \( E \rightarrow \infty\).
Рис. 4. Граф для параллельного сложения 8-ми чисел
Реализация каскадного метода в параллельном режиме имеет смысл только для \(n/2\) ядер.
Комбинированный метод
Пусть число процессоров равно \(p(p Параллельные алгоритмы вычисления суммы
Граф для комбинированного метода представлен на рис. 5. В этом графе предполагается, что число слагаемых равно 8, а число ядер процессора – 2.
В этом случае время параллельных вычислений составляет:
Это же высота графа. Степень параллелизма на шаге 1 равна \(р\), на последующих шагах \(p/2, p/4,…, 1\). Таким образом, степени параллелизма образуют убывающую геометрическую прогрессию со знаменателем 0.5. Средняя степень параллелизма равна:
В этой формуле число членов прогрессии равно \(log_<2>p +1\). Для получения данной формулы используется формула для вычисления значения n-ого члена прогрессии \(b_1\frac<1-q^n><1-q>\). Определим значение средней степени параллелизма для графа на рис. 5. На первом шаге степень параллелизма равна 2, на втором 1, среднее значение равно 1.5. Для приведенной выше формулы получаем при \(р = 2\) значение 1.5.
Определим показатели уско> Каскадный метод вычисления суммы
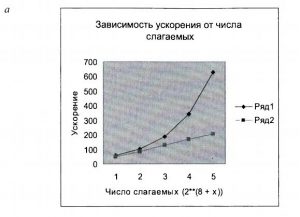
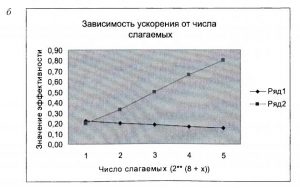
Ниже представлены графики изменения ускорения (рис. 6а) и эффективности (рис. 6б) в зависимости от числа слагаемых для каскадного (Ряд 1) и комбинированного (Ряд 2) метода.
Рис. 5. Граф комбинированной схемы
Из графиков следует, что для каскадного метода ускорение растет с увеличением числа слагаемых, но медленнее, чем число необходимых ядер процессора. Так, для числа слагаемых 512 требуется 256 ядер, и ускорение составляет приблизительно 57, а для числа слагаемых 8192 число ядер равно 4096, а ускорение составляет 630. Таким образом, увеличение числа слагаемых в 16 раз приводит к увеличению ускорения в 11 раз. Изменение скорости роста фактически отражает показатель эффективности, который падает с увеличением числа слагаемых. Для комбинированного метода эффективность растет. Кроме того, с помощью комбинированного метода можно решить задачу с любым числом ядер и числом слагаемых. Для каскадного метода требуется число ядер, которое на сегодня является нереальным.
Рис. 6. Зависимость ускорения и эффективности для каскадного и комбинированного методов вычисления суммы
Заметим, что этот же принцип вычисления можно использовать для вычисления произведения элементов массива, минимального и максимального элементов.
Вычисление частичных сумм
Пусть необходимо вычислить:
В последовательном режиме для решения этой задачи необходимо выполнить такое же число операций, как для вычисления согласно (2), т.е. \(n–1\) операций.
Каскадный метод в чистом виде для решения этой задачи неприменим. Модифицируем этот метод:
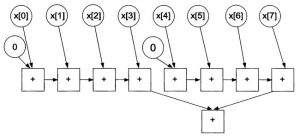
Шаг 1. Сдвинем массив \(S\) на 1 элемент вправо. Свободный элемент слева сделаем равным 0, последний элемент массива \(х\) теряется. Выполним покомпонентное суммирование элементов массива \(S\) их. В результате получим значения:
В результате выполнения первого шага получаем правильные значения \(S_<0>-S_<1>\). Остальные значения необходимо дополнять. Для выполнения шага 1 при наличии n ядер требуется одна операция, включающая в себя сдвиг и сложение.
Шаг 2. Вычисляем значение \(S = (S>>2) + S\)
Шаг 3. Вычисляем значение \(S = (S>>4) + S\):
В результате выполнения шага 3 получили все правильные значения \(S\). Для выполнения шага 3 при наличии \(n\) ядер требуется одна операция, включающая в себя сдвиг и сложение. Граф для вычисления частичных сумм для массива с 8-ми элементами представлен на рис. 6.
Рис. 6. Параллельный алгоритм вычисления частичных сумм
Таким образом, общее число шагов для восьми слагаемых равно \(log_<2>n\) (высота графа). Степень параллелизма на каждом шаге равна числу элементов массива \(n\).
Общий вид алгоритма:
Все итерации цикла по i независимы, шаги необходимо выполнять последовательно, переход на очередной шаг допустим после полного завершения предыдущего шага.
Можно считать, что в цикле для каждого шага необходимо выполнить 2 операции: вычисление константы сдвига и параллельное вычисление новых значений элементов массива \(S[i]\), в этом случае общее количество операций для каскадного метода составляет \(2*log_<2>n\) Определим показатели ускорения и эффективности:
Для рассмотренного алгоритма требуется процессор с \(n\) ядрами. Для уменьшения числа необходимых ядер внутренний цикл можно считать параллельно-последовательно, определив число порций по количеству доступных ядер. Каждая порция выполняется последовательно.
Заметим, что выигрыш получаем только при \(n > 4\), реализация алгоритма в случае двух потоков не имеет смысла, так как эта реализация будет сложнее, чем для алгоритма вычисления обычной суммы, а для последнего алгоритма мы не получили выигрыша.
Основные вычислительные алгоритмы
Составные (сложные).
Простые.
Перечислимый тип может хранить только те значения, которые прямо указаны в его описании:
-числовые. Хранятся числа, могут применяться обычные арифметические операции;
-целочисленные: со знаком, то есть могут принимать как положительные, так и отрицательные значения, и без знака, то есть могут принимать только неотрицательные значения;
-вещественные: с запятой и с плавающей запятой;
-числа произвольной точности, обращение с которыми происходит посредством длинной арифметики;
-символьный тип. Хранит один символ, могут использоваться различные кодировки;
-логический тип: имеет два значения: истина и ложь, могут применяться логические операции. Используется в операторах ветвления и циклах. В некоторых языках является подтипом числового типа, при этом ложь=0, истина=1;
-множество. В основном совпадает с обычным математическим понятием множества. Допустимы стандартные операции с множествами и проверка на принадлежность элемента множеству. В некоторых языках рассматривается как составной тип.
— массив — упорядоченный набор данных, для хранения данных одного типа, идентифицируемых с помощью одного или нескольких индексов. В простейшем случае массив имеет постоянную длину и хранит единицы данных одного и того же типа. Количество используемых индексов массива может быть различным. Массивы с одним индексом называют одномерными, с двумя — двумерными и т. д. Одномерный массив нестрого соответствует вектору в математике., двумерный — матрице. Чаще всего применяются массивы с одним или двумя индексами, реже — с тремя, ещё большее количество индексов встречается крайне редко;
— строковый тип. Хранит строку символов. Аналогом сложения в строковой алгебре является конкатенация (прибавление одной строки в конец другой строки). В языках, близких к бинарному представлению данных, чаще рассматривается как массив символов, в языках более высокой абстракции зачастую выделяется в качестве простого;
— запись (структура). Набор различных элементов (полей записи), хранимый как единое целое. Возможен доступ к отдельным полям записи. Например, struct в С или record в Pascal;
— файловый тип. Хранит только однотипные значения, доступ к которым осуществляется только последовательно (файл с произвольным доступом, включенный в некоторые системы программирования, фактически является неявным массивом).
Алгоритмические (или вычислительные) процессы обработки данных делятся на виды:
Линейным называется такой вычислительный процесс, в котором самостоятельные этапы вычислений выполняются в последовательности их записи, т.е. в естественном порядке.
Каждая операция является самостоятельной, независимой от каких-либо условий.
Линейные вычислительные процессы имеют место при вычислении арифметических выражений.
Ветвящимсяназывается такой процесс, в котором его реализация происходит по одному из нескольких заранее предусмотренных (возможных) направлений в зависимости от исходных условий или промежуточных результатов. Каждое отдельное направление вычислений в таком процессе называется ветвью вычисления. Выбор осуществляется проверкой выполнения логического условия.
В каждом конкретном случае обработки данных вычислительный процесс выполняется лишь по одной ветви, а выполнение остальных – исключается.
Ветвящийся процесс, включающий в себя две ветви, называется простым, более двух ветвей- сложным. Сложный ветвящийся процесс можно представить с помощью простых ветвящихся процессов.
Любая ветвь, по которой осуществляются вычисления, должна приводить к завершению вычислительного процесса.
При реализации алгоритмов многих задач наблюдается многократное повторение отдельных этапов их вычислительного процесса. Такие многократно повторяемые этапы вычислений называются циклами, а вычислительные процессы, содержащие многократно повторяемые этапы называются циклическими.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет