Что такое выходное сопротивление антенны
Что такое выходное сопротивление антенны
Что такое входное сопротивление антенны и что с ним делать?
Все знают, что входное сопротивление (импеданс) антенны редко когда бывает равный волновому сопротивлению фидерной линии. Здесь постараюсь показать, как согласовать нагрузку с фидером эффективными методами. Далее все примеры будут даны для коаксиального кабеля с волновым сопротивлением 50 ом, но принцип расчёта действителен и для других как несимметричных, так и симметричных линий передач.
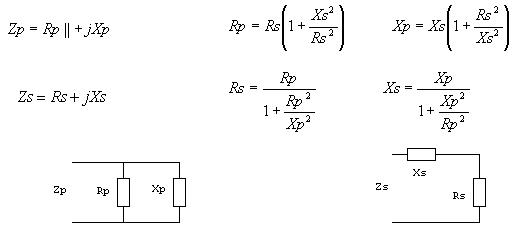
Например, пересчитаем последовательное соединение Zs=40+j30 W в параллельное Zp.
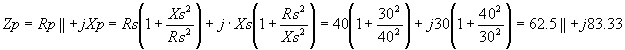
Чаще используют эквивалент последовательного включения, но и эквивалент параллельного включения имеет такое же практическое значение. Zs называется импедансом последовательного включения, R – резистансом, X – реактансом, а Zp импедансом параллельного включения. В параллельном включении часто используется админтанс, но это проводимость, и наглядность при его использовании сильно уменьшается. Обычно термин „импеданс“ указывает, что речь идёт о последовательном соединении эквивалентного активного и реактивного сопротивлений. Однако, пересчёт последовательного соединения сопротивлений в параллельное соединение довольно часто нужен для компенсации реактивной составляющей. Только следует иметь в виду, что при последовательной и параллельной компенсации получаем разные активные составляющие сопротивления. Для пересчёта Zs в Zp и наоборот очень хорошо подходит программа NETCALK. Можно посчитать и здесь.
Rs = Xs = Zp» onclick=»skaiciuok(‘zszp’)»>
Rp = Xp = Zs» onclick=»skaiciuok(‘zpzs’)» />
SWR =
Возникает вопрос, как измерить параметры комплексной нагрузки. К сожалению, простой измеритель КСВ тут мало пригоден. Я для этого пользуюсь векторным анализатором VA1, который на дисплее показывает все нужные цифровые значения.
Компенсация реактивной составляющей
Реактивную составляющую сопротивления (импеданса) полезно компенсировать. Это уменьшает КСВ. Суть компенсации есть выравнивания фаз напряжения и тока. Менять угол фазы между напряжением и током можно подключая реактивный элемент последовательно или параллельно. Чтобы разница в углах фаз стала равна нулю, надо подключить такое реактивное сопротивление, какое присутствует в эквивалентной схеме нагрузки, только с противоположным знаком. Известно, что реактивное сопротивление ёмкости имеет отрицательный знак, индуктивности – положительный. В случае последовательной компенсации дополнительный эквивалентный реактивный элемент с противоположным знаком включается последовательно и получается последовательный контур, а в случае параллельной компенсации – параллельно, получается параллельный контур. В случае последовательного соединения сопротивлений они просто складываются

А в случае параллельного соединения

Как видим, согласовать можно, подключив индуктивность 1,35 m H параллельно нагрузке, а сигнал на нагрузку подавать через конденсатор 68,5pF.
Шлейфы
Шлейфами называются закороченые или открытые отрезки фидера. В идеальном фидере (фидере без потерь) сопротивление таких отрезков есть чисто реактивное, активной части нет. Такими отрезками фидера можно пользоваться при компенсации реактивной составляющей. Это удобно, если применяется параллельное компенсирование. Часто используется отрезки до четверти длины волны. Они могут быть и длиннее, но реальные фидеры имеют потери и, чем длиннее линия, тем больше. Замкнутый шлейф электрической длины до 1/4 l имеет на конце индуктивное реактивное сопротивление, разомкнутый – ёмкостное. Такими отрезками фидера можно имитировать как индуктивность, так и ёмкость. Но надо не забыть, что индуктивность или ёмкость шлейфа зависят от частоты. В приведённом примере мы видим, что надо подключить индуктивность 1,352 m H. С помощью MMANA получаем, что такую индуктивность на 14 MHz имеет закороченный на конце шлейф с кабеля RG58/U длиной 2,62м.
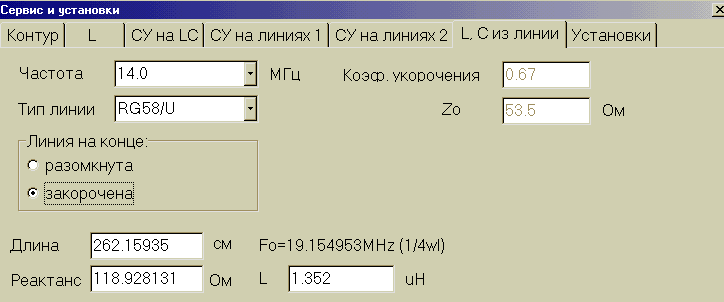
На том же примере попробуем то же согласовать с помощью MMANA другим способом, используя только шлейф.
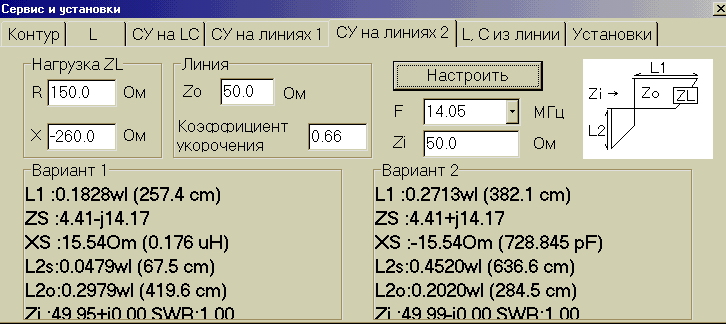
Таким образом, если короткозамкнутый шлейф длиной 67,5см. подключить параллельно фидеру на расстоянии 2,57м. от нагрузки, то так же полностью согласуем фидер с нагрузкой. Или же, можно параллельно подключить разомкнутый шлейф длиной 2,84м. на расстоянии от нагрузки 3,82м. Возможны и другие варианты согласования. Но следует помнить, что потери в низкоомных (коаксиальных) фидерах при больших величинах КСВ значительны, так что желательно выбирать такой способ согласования, при котором получаются самые короткие отрезки фидера с большим КСВ и применять толстые качественные кабеля.
Как видите, практически можно согласовать все и по-разному. Только для этого нужен измерительный прибор, ну, и конечно, компьютер. Комплексное сопротивление антенны не измеришь ни тестером, ни измерителем КСВ. Без этих данных согласование превращается в трудоёмкое занятие и часто приводит к неудовлетворительным результатам. В этой статье я описал несколько методов согласования. Постарался описать суть вопроса как можно проще, но очень просто в таком вопросе не получается.
Эта статья мною написана несколько лет назад на литовском языке и сейчас переведена на русский. В настоящее время имеются другие версии программ APAK-EL и MMANA, примеры же приведены используя старые версии. APAK-EL имеет утилиту, с помощю которой тоже можно рассчитать компенсирующие реактивности. Однако сам принцип согласования от этого не меняется.
Надеюсь, что статья кое-кому будет полезна.
Входное и выходное сопротивление
Входное и выходное сопротивление является очень важным в электронике.
Предисловие
Ладно, начнем издалека… Как вы знаете, все электронные устройства состоят из блоков. Их еще часто называют каскады, модули, узлы и тд. В нашей статье будем использовать понятие «блок». Например, источник питания, собранный по этой схеме:
состоит из двух блоков. Я их пометил в красном и зеленом прямоугольниках.
В красном блоке мы получаем постоянное напряжение, а в зеленом блоке мы его стабилизируем. То есть блочная схема будет такой:
Блочная схема — это условное деление. В этом примере мы могли бы даже взять трансформатор, как отдельный блок, который понижает переменное напряжение одного номинала к другому. Как нам удобнее, так и делим на блоки нашу электронную безделушку. Метод «от простого к сложному» полностью работает в нашем мире. На низшем уровне находятся радиоэлементы, на высшем — готовое устройство, например, телевизор.
Ладно, что-то отвлеклись. Как вы поняли, любое устройство состоит из блоков, которые выполняют определенную функцию.
— Ага! Так что же получается? Я могу просто тупо взять готовые блоки и изобрести любое электронное устройство, которое мне придет в голову?
Да! Именно на это нацелена сейчас современная электроника 😉 Микроконтроллеры и конструкторы, типа Arduino, добавляют еще больше гибкости в творческие начинания молодых изобретателей.
На словах все выходит прекрасно, но всегда есть подводные камни, которые следует изучить, чтобы начать проектировать электронные устройства. Некоторые из этих камушков называются входным и выходным сопротивлением.
Думаю, все помнят, что такое сопротивление и что такое резистор. Резистор хоть и обладает сопротивлением, но это активное сопротивление. Катушка индуктивности и конденсатор будут уже обладать, так называемым, реактивным сопротивлением. Но что такое входное и выходное сопротивление? Это уже что-то новенькое. Если прислушаться к этим фразам, то входное сопротивление — это сопротивление какого-то входа, а выходное — сопротивление какого-либо выхода. Ну да, все почти так и есть. И где же нам найти в схеме эти входные и выходные сопротивления? А вот «прячутся» они в самих блоках радиоэлектронных устройств.
Входное сопротивление
Итак, имеем какой-либо блок. Как принято во всем мире, слева — это вход блока, справа — выход.
Как и полагается, этот блок используется в каком-нибудь радиоэлектронном устройстве и выполняет какую-либо функцию. Значит, на его вход будет подаваться какое-то входное напряжение Uвх от другого блока или от источника питания, а на его выходе появится напряжение Uвых (или не появится, если блок является конечным).
Но раз уж мы подаем напряжение на вход (входное напряжение Uвх), следовательно, у нас этот блок будет кушать какую-то силу тока Iвх.
Теперь самое интересное… От чего зависит Iвх ? Вообще, от чего зависит сила тока в цепи? Вспоминаем закон Ома для участка цепи :
Значит, сила тока у нас зависит от напряжения и от сопротивления. Предположим, что напряжение у нас не меняется, следовательно, сила тока в цепи будет зависеть от… СОПРОТИВЛЕНИЯ. Но где нам его найти? А прячется оно в самом каскаде и называется входным сопротивлением.
То есть, разобрав такой блок, внутри него мы можем найти этот резистор? Конечно же нет). Он является своего рода сопротивлением радиоэлементов, соединенных по схеме этого блока. Скажем так, совокупное сопротивление.
Как измерить входное сопротивление
Как мы знаем, на каждый блок подается какой-либо сигнал от предыдущего блока или это может быть даже питание от сети или батареи. Что нам остается сделать?
1)Замерить напряжение Uвх, подаваемое на этот блок
2)Замерить силу тока Iвх, которую потребляет наш блок
3) По закону Ома найти входное сопротивление Rвх.
Если у вас входное сопротивление получается очень большое, чтобы замерить его как можно точнее, используют вот такую схему.
Мы с вами знаем, что если входное сопротивление у нас большое, то входная сила тока в цепи у нас будет очень маленькая (из закона Ома).
Падение напряжения на резисторе R обозначим, как UR
Из всего этого получаем…
Когда мы проводим эти измерения, имейте ввиду, что напряжение на выходе генератора не должно меняться!
Итак, давайте посчитаем, какой же резистор нам необходимо подобрать, чтобы как можно точнее замерять это входное сопротивление. Допустим, что у нас входное сопротивление Rвх=1 МегаОм, а резистор взяли R=1 КилоОм. Пусть генератор выдает постоянное напряжение U=10 Вольт. В результате, у нас получается цепь с двумя сопротивлениями. Правило делителя напряжения гласит: сумма падений напряжений на всех сопротивлениях в цепи равняется ЭДС генератора.
В результате получается цепь:
Высчитываем силу тока в цепи в Амперах
Получается, что падение напряжения на сопротивлении R в Вольтах будет:
Грубо говоря 0,01 Вольт. Вряд ли вы сможете точно замерить такое маленькое напряжение на своем китайском мультиметре.
Какой отсюда вывод? Для более точного измерения высокого входного сопротивления надо брать добавочное сопротивление также очень большого номинала. В этом случае работает правило шунта: на бОльшем сопротивлении падает бОльшее напряжение, и наоборот, на меньшем сопротивлении падает меньшее напряжение.
Измерение входного сопротивления на практике
Ну все, запарка прошла ;-). Давайте теперь на практике попробуем замерить входное сопротивление какого-либо устройства. Мой взгляд сразу упал на Транзистор-метр. Итак, выставляем на блоке питания рабочее напряжение этого транзистор-метра, то есть 9 Вольт, и во включенном состоянии замеряем потребляемую силу тока. Как замерить силу тока в цепи, читаем в этой статье. По схеме все это будет выглядеть вот так:
Итак, у нас получилось 22,5 миллиАмпер.
Теперь, зная значение потребляемого тока, можно найти по этой формуле входное сопротивление:
Выходное сопротивление
Яркий пример выходного сопротивления — это закон Ома для полной цепи, в котором есть так называемое «внутреннее сопротивление». Кому лень читать про этот закон, вкратце рассмотрим его здесь.
Что мы имели? У нас был автомобильный аккумулятор, с помощью которого мы поджигали галогенную лампочку. Перед тем, как цеплять лампочку, мы замеряли напряжение на клеммах аккумулятора:
И как только подсоединяли лампочку, у нас напряжение на аккумуляторе становилось меньше.
Разница напряжения, то есть 0,3 Вольта (12,09-11,79) у нас падало на так называемом внутреннем сопротивлении r 😉 Оно же и есть ВЫХОДНОЕ СОПРОТИВЛЕНИЕ. Его также называют еще сопротивлением источника или эквивалентным сопротивлением.
У всех аккумуляторов есть это внутреннее сопротивление r, и «цепляется» оно последовательно с источником ЭДС (Е).
Но только ли аккумуляторы и различные батарейки обладают выходным сопротивлением? Не только. Выходным сопротивлением обладают все источники питания. Это может быть блок питания, генератор частоты, либо вообще какой-нибудь усилитель.
В теореме Тевенина (короче, умный мужик такой был) говорилось, что любую цепь, которая имеет две клеммы и содержит в себе туеву кучу различных источников ЭДС и резисторов разного номинала можно привести тупо к источнику ЭДС с каким-то значением напряжения (Eэквивалентное) и с каким-то внутренним сопротивлением (Rэквивалентное).
Eэкв — эквивалентный источник ЭДС
Rэкв — эквивалентное сопротивление
То есть получается, если какой-либо источник напряжения питает нагрузку, значит, в источнике напряжения есть ЭДС и эквивалентное сопротивление, оно же выходное сопротивление.
В режиме холостого хода (то есть, когда к выходным клеммам не подцеплена нагрузка) с помощью мультиметра мы можем замерить ЭДС (E). С замером ЭДС вроде бы понятно, но вот как замерить Rвых ?
В принципе, можно устроить короткое замыкание. То есть замкнуть выходные клеммы толстым медным проводом, по которому у нас будет течь ток короткого замыкания Iкз.
В результате у нас получается замкнутая цепь с одним резистором. Из закона Ома получаем, что
Но есть небольшая загвоздка. Теоретически — формула верна. Но на практике я бы не рекомендовал использовать этот способ. В этом случае сила тока достигает бешеного значения, да вообще, вся схема ведет себя неадекватно.
Измерение выходного сопротивления на практике
Есть другой, более безопасный способ. Не буду повторяться, просто скопирую со статьи закон Ома для полной цепи, где мы находили внутреннее сопротивление аккумулятора. В той статье, мы к акуму цепляли галогенную лампочку, которая была нагрузкой R. В результате по цепи шел электрический ток. На лампочке и на внутреннем сопротивлении у нас падало напряжение, сумма которых равнялась ЭДС.
Итак, для начала замеряем напряжение на аккумуляторе без лампочки.
Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае E=12,09 Вольт.
Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем резисторе и на нагрузке, в данном случае на лампочке:
Сейчас на нагрузке (на галогенке) у нас упало напряжение UR=11,79 Вольт, следовательно, на внутреннем резисторе падение напряжения составило Ur=E-UR=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r:
Заключение
Входное и выходное сопротивление каскадов (блоков) в электронике играют очень важную роль. В этом мы убедимся, когда начнем рассматривать статью по согласованию узлов радиоэлектронных схем. Все качественные вольтметры и осциллографы также стараются делать с очень высоким входным сопротивлением, чтобы оно меньше сказывалось на замеряемый сигнал и не гасило его амплитуду.
С выходным сопротивлением все намного интереснее. Когда мы подключаем низкоомную нагрузку, то чем больше внутреннее сопротивление, тем больше напряжение падает на внутреннем сопротивлении. То есть в нагрузку будет отдаваться меньшее напряжение, так как разница осядет на внутреннем резисторе. Поэтому, качественные источники питания, типа блока питания либо генератора частоты, пытаются делать как можно с меньшим выходным сопротивлением, чтобы напряжение на выходе «не проседало» при подключении низкоомной нагрузки. Даже если сильно просядет, то мы можем вручную подкорректировать с помощью регулировки выходного напряжения, которые есть в каждом нормальном источнике питания. В некоторых источниках это делается автоматически.
Что такое выходное сопротивление антенны
Что такое входное сопротивление антенны и что с ним делать?
Все знают, что входное сопротивление (импеданс) антенны редко когда бывает равный волновому сопротивлению фидерной линии. Здесь постараюсь показать, как согласовать нагрузку с фидером эффективными методами. Далее все примеры будут даны для коаксиального кабеля с волновым сопротивлением 50 ом, но принцип расчёта действителен и для других как несимметричных, так и симметричных линий передач.
Например, пересчитаем последовательное соединение Zs=40+j30 W в параллельное Zp.
Чаще используют эквивалент последовательного включения, но и эквивалент параллельного включения имеет такое же практическое значение. Zs называется импедансом последовательного включения, R – резистансом, X – реактансом, а Zp импедансом параллельного включения. В параллельном включении часто используется админтанс, но это проводимость, и наглядность при его использовании сильно уменьшается. Обычно термин „импеданс“ указывает, что речь идёт о последовательном соединении эквивалентного активного и реактивного сопротивлений. Однако, пересчёт последовательного соединения сопротивлений в параллельное соединение довольно часто нужен для компенсации реактивной составляющей. Только следует иметь в виду, что при последовательной и параллельной компенсации получаем разные активные составляющие сопротивления. Для пересчёта Zs в Zp и наоборот очень хорошо подходит программа NETCALK. Можно посчитать и здесь.
Rs = Xs = Zp» onclick=»skaiciuok(‘zszp’)»>
Rp = Xp = Zs» onclick=»skaiciuok(‘zpzs’)» />
SWR =
Возникает вопрос, как измерить параметры комплексной нагрузки. К сожалению, простой измеритель КСВ тут мало пригоден. Я для этого пользуюсь векторным анализатором VA1, который на дисплее показывает все нужные цифровые значения.
Компенсация реактивной составляющей
Реактивную составляющую сопротивления (импеданса) полезно компенсировать. Это уменьшает КСВ. Суть компенсации есть выравнивания фаз напряжения и тока. Менять угол фазы между напряжением и током можно подключая реактивный элемент последовательно или параллельно. Чтобы разница в углах фаз стала равна нулю, надо подключить такое реактивное сопротивление, какое присутствует в эквивалентной схеме нагрузки, только с противоположным знаком. Известно, что реактивное сопротивление ёмкости имеет отрицательный знак, индуктивности – положительный. В случае последовательной компенсации дополнительный эквивалентный реактивный элемент с противоположным знаком включается последовательно и получается последовательный контур, а в случае параллельной компенсации – параллельно, получается параллельный контур. В случае последовательного соединения сопротивлений они просто складываются
А в случае параллельного соединения
Как видим, согласовать можно, подключив индуктивность 1,35 m H параллельно нагрузке, а сигнал на нагрузку подавать через конденсатор 68,5pF.
Шлейфы
Шлейфами называются закороченые или открытые отрезки фидера. В идеальном фидере (фидере без потерь) сопротивление таких отрезков есть чисто реактивное, активной части нет. Такими отрезками фидера можно пользоваться при компенсации реактивной составляющей. Это удобно, если применяется параллельное компенсирование. Часто используется отрезки до четверти длины волны. Они могут быть и длиннее, но реальные фидеры имеют потери и, чем длиннее линия, тем больше. Замкнутый шлейф электрической длины до 1/4 l имеет на конце индуктивное реактивное сопротивление, разомкнутый – ёмкостное. Такими отрезками фидера можно имитировать как индуктивность, так и ёмкость. Но надо не забыть, что индуктивность или ёмкость шлейфа зависят от частоты. В приведённом примере мы видим, что надо подключить индуктивность 1,352 m H. С помощью MMANA получаем, что такую индуктивность на 14 MHz имеет закороченный на конце шлейф с кабеля RG58/U длиной 2,62м.
На том же примере попробуем то же согласовать с помощью MMANA другим способом, используя только шлейф.
Таким образом, если короткозамкнутый шлейф длиной 67,5см. подключить параллельно фидеру на расстоянии 2,57м. от нагрузки, то так же полностью согласуем фидер с нагрузкой. Или же, можно параллельно подключить разомкнутый шлейф длиной 2,84м. на расстоянии от нагрузки 3,82м. Возможны и другие варианты согласования. Но следует помнить, что потери в низкоомных (коаксиальных) фидерах при больших величинах КСВ значительны, так что желательно выбирать такой способ согласования, при котором получаются самые короткие отрезки фидера с большим КСВ и применять толстые качественные кабеля.
Как видите, практически можно согласовать все и по-разному. Только для этого нужен измерительный прибор, ну, и конечно, компьютер. Комплексное сопротивление антенны не измеришь ни тестером, ни измерителем КСВ. Без этих данных согласование превращается в трудоёмкое занятие и часто приводит к неудовлетворительным результатам. В этой статье я описал несколько методов согласования. Постарался описать суть вопроса как можно проще, но очень просто в таком вопросе не получается.
Эта статья мною написана несколько лет назад на литовском языке и сейчас переведена на русский. В настоящее время имеются другие версии программ APAK-EL и MMANA, примеры же приведены используя старые версии. APAK-EL имеет утилиту, с помощю которой тоже можно рассчитать компенсирующие реактивности. Однако сам принцип согласования от этого не меняется.
Надеюсь, что статья кое-кому будет полезна.
Про антенны для самых маленьких
Попробуем разобраться, как работают антенны и почему электромагнитная энергия из комфортного проводника излучается в чужеродный диэлектрик, причем обойдемся без матана, что потребует, разумеется, очень серьезных упрощений и даже вульгаризации, но все же позволит получить начальное представление и, не исключаю, желание почитать материалы для более продвинутых.
Если вы радиоинженер, опытный радиолюбитель-связист или просто хорошо знаете физику, то вам нижеследующее читать строго не рекомендуется во избежание негативных последствий для вашего психического здоровья. Вас предупреждали.
Начнем со скучных основ. В старые добрые времена, когда не было ни интернетов, ни этого вашего фидо, известные явления электричества и магнетизма не считались чем-то единым, имеющим общую природу, пока ровно двести лет назад датчанин Эрстед не обнаружил, что протекание электрического тока по проводнику вызывает отклонение стрелки компаса, т.е. создает доступное наблюдению и измерению простейшими приборами магнитное поле.
Вскорости француз Ампер вывел закон имени себя, описывающий зависимость электрического тока и возникающего от него магнитного поля, а чуть позже включившийся англичанин Фарадей обнаружил и математически изложил явление электромагнитной индукции. Спустя еще совсем немного времени шотландец Максвелл создает теорию электромагнитного поля, на которую нам бы и следовало опираться в дальнейшем рассказе, но мы договорились обходиться без матана настолько, насколько возможно, чтобы даже самые отпетые гуманитарии смогли почувствовать вкус к технике вместо быть распуганными сложными формулами. Все эти работы привели к тому, что 1887 году немец Герц экспериментально доказал существование радиоволн, построив радиопередатчик и радиоприемник, которые, довольно неожиданно, оказались рабочими. Впрочем, сам Герц перспектив своей радиопередачи (первой в мире!) не оценил и поэтому изобретение радио чаще связывают с итальянцем Маркони, который помимо неоспоримого инженерного гения, оказался успешен и в части коммерциализации. Да, если кому интересно, первая радиопередача голоса принадлежит канадцу Фесендену, которому удалось провернуть это дело в 1900 году.
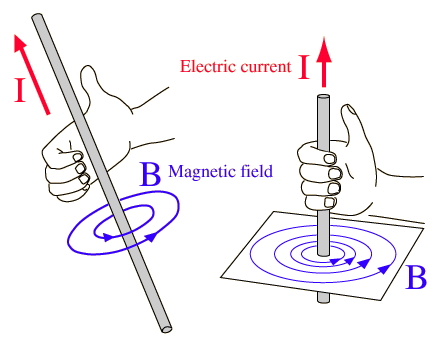
Ток в проводнике создает магнитное поле. Зачем же нам браться рукой за оголенный провод? Затем, чтобы легко запомнить направление вектора магнитного поля в зависимости от направления тока в проводнике — «правило правой руки».
Итак, теперь мы знаем, что протекание электрического тока в проводнике приводит к тому, что около проводника возникает магнитное поле. Вот это вот, если очень-очень упрощенно, и есть электромагнетизм. Поэтому первое, что мы можем усвоить: излучение антенн связано с протеканием в них электрического тока.
Радиосвязь использует переменный ток различной частоты (или длины волны – говоря об антеннах чаще удобнее говорить о длине волны, а о радиотехнике в целом – о частоте).
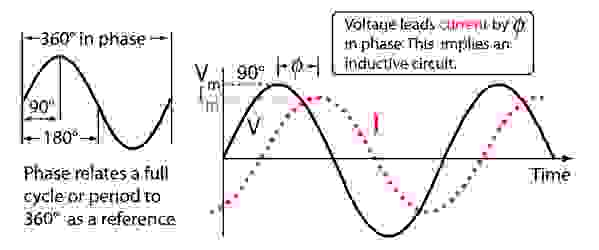
Различные частоты позволяют одновременно проводить много независимых передач и разделять их прием, выбирая нужные частоты и отбрасывая ненужные. Способов, как это сделать, довольно много, но они — тема отдельных статей. Переменный ток обладает одной неприятной особенностью: хотя он полностью подчиняется закону Ома (взаимозависимость напряжения, сопротивления цепи и тока в ней), напряжение и ток могут не совпадать по времени. Да-да, «сдвиг по фазе» – это необязательно в голове, это более чем электро- и радиотехнический термин. Вот что получается. Если бы мы подавали переменное напряжение на некий идеальный резистор, то синфазный переменный ток в этой цепи был бы равен напряжению в вольтах, деленному на сопротивление в омах – так же, как и приличный постоянный ток. Но если вместо резистора у нас катушка индуктивности, то дело становится более запутанным. Когда мы прикладываем напряжение к катушке, она как бы сопротивляется току через нее, поэтому ток отстает по фазе от напряжения. Кстати, если отключить подачу напряжения от катушки, то она тоже будет сопротивляться и постарается поддержать течение тока через себя (в той мере, в которой катушка может запасти энергию) – напряжения уже нет, а ток все еще идет. Вот это вот сопротивление, оно называется реактивным, тем выше, чем выше частота. То есть с ростом частоты при равной индуктивности или с ростом индуктивности при равной частоте сопротивление переменному току растет. С конденсаторами все то же самое, но только наоборот. При приложении напряжения к конденсатору ток сначала проваливается в него, как в пустую яму, опережая напряжение, а затем падает по мере заряда. Легкость, с которой переменный ток попадает в конденсатор, означает, что с ростом частоты при равной емкости сопротивление переменному току падает, а при равной частоте при росте емкости сопротивление переменному току также падает. Поэтому примем на заметку: реактивное сопротивление, то есть индуктивное или емкостное сопротивление переменному току, зависит от частоты.
Слева традиционная синусоидальная осциллограмма, справа сдвиг фаз на примере «отставания» тока от напряжения при наличии в цепи индуктивного сопротивления.
Суммарное сопротивление, состоящее из активной компоненты (условный резистор, который потребляет мощность «чисто», без влияния на фазу) и реактивной компоненты (сдвигающие фазу индуктивность и/или емкость), называется комплексным сопротивлением или импедансом.
Итак, антенна – это проводник, к которому подводится электрическая энергия и который ее излучает в окружающее пространство. Излучает электрический ток в проводнике, который создает вокруг проводника магнитное поле.
Почему электромагнитная энергия выходит из комфортного для нее проводника в некомфортный для нее вакуум? А она и не выходит! Энергия создает колебания поля, но не движется сама по себе. Давайте сравним со звуковыми волнами. Когда динамик (антенна) создает колебания, воздух (эфир) не движется, ветер не возникает, но колебания распространяются в воздухе (эфире). Так же происходит и с электромагнитными волнами, разве что электромагнитная энергия распространяется не в воздухе, а в эфире. Позже, правда, выяснят, что предполагавшегося эфира не существует, и что земля тоже не плоская, а электромагнитное поле прекрасно себя чувствует и в вакууме но мы-то знаем, что эфир есть, а земля, конечно, не плоская, а немного выпуклая. То есть, еще раз, энергия не переносится вместе со средой (точнее с полем), а переносится за счет распространения волн в неподвижной в общем случае среде (в поле).
Антенна как колебательный контур. Прежде чем говорить о конкретных конструкциях простых антенн, по принципу устройства которых мы сможем разобраться и в устройстве сложных, поговорим об электрическом резонансе. Для этого вернемся назад к реактивному сопротивлению. Полотно антенны можно представить как распределенную емкость и распределенную индуктивность – как размотанную до прямого провода катушку и как вырожденные до того же самого провода пластины конденсатора. Наличие реактивного сопротивления в цепи, как мы помним, разделяет фазы тока и напряжения. Однако, если мы подберем определенную комбинацию индуктивности и емкости (а это сработает только на одной определенной частоте, ведь мы помним, что с изменением частоты меняется реактивное сопротивление), то получится, что емкость и индуктивность взаимно компенсируют друг друга и мы видим чисто активное сопротивление в нагрузке. Вот такая взаимная компенсация и результат в виде чисто активного сопротивления как результат компенсации называется электрическим резонансом. Сам по себе для работы антенны он неважен, потому что антенна, как мы уже выяснили, излучает током в проводнике. Однако, есть ряд причин, по которым к достижению резонанса в антенне стремятся. Дело в том, что в отличие от постоянного тока, для переменного важно, чтобы волновое сопротивление (напоминаю закон Ома, а именно что сопротивление цепи численно равно приложенному напряжению, деленному на ток) генератора, линии передачи и нагрузки, т.е. собственно антенны, были равны. Если равенства нет, часть электромагнитной энергии отразится назад на генератор, что приведет к целому спектру нежелательных явлений. Значительное реактивное сопротивление приводит к сильному рассогласованию и значительному отражению энергии. Впрочем, это касается и активной компоненты импеданса, согласовать которую легче при незначительной, легко компенсируемой реактивной компоненте. Поэтому технически стараются создавать такие антенны, у которых реактивная компонента отсутствует или легко компенсируется, а активная равна волновому сопротивлению генератора или легко трансформируется. В случае самых простых антенн, создание определенной емкости антенны или определенной индуктивности означает попросту подбор размеров. Поэтому обычно размеры антенн меряют не в линейных единицах, а в долях длины волны.
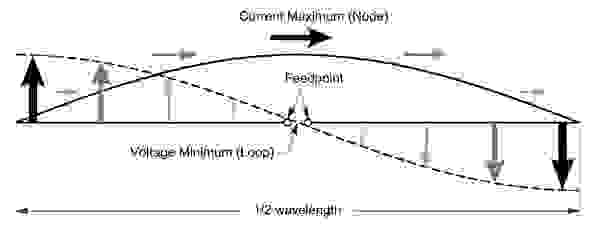
Простейшие полноразмерные антенны. Полуволновый диполь, четвертьволновый граундплейн и аналогичные конструкции.
Как видим, распределение токов и напряжений одинаково. Только если в четвертьволновом граундплейне одна половина диполя — штырь, а второй половиной является земля, то в полуволновом диполе — второй половиной является его вторая половина. 🙂
Для ознакомления с принципами, одинаковыми для любых более сложных антенн, предлагаю разобраться с устройством и работой базовых антенн – симметричного полуволнового диполя или несимметричного четвертьволнового граундплейна. В известной степени они идентичны и полуволновый диполь можно рассматривать как крайний случай четвертьволнового граундплейна, угол радиалов (противовесов) которого достиг 180° к излучающему штырю, поэтому большинство рассматриваемых особенностей в равной мере применимы к обоим антеннам.
Как видим, такая антенна имеет электрический резонанс, потому что в ее проводнике помещается целое число полуволн тока и целое число полуволн напряжения. Они смещены по фазе друг относительно друга, но их реактивность взаимно компенсируется.
Если бы антенна была немного короче, чем полволны, то у нее бы появилась емкостная компонента импеданса и ее пришлось бы компенсировать индуктивностью (никому не напоминает катушки в основании сибишных автоантенн?), а если наоборот удлинить, то появится индуктивная компонента, которую необходимо скомпенсировать емкостью.
Сопротивление излучения. В сопротивлении излучения нет ничего особенного. Вернее не так. Сопротивления излучения в физическом смысле не существует, это аналитическое значение, которое используется для определения КПД антенны. Проще всего представить себе сопротивление излучения как ту активную компоненту полного сопротивления всей антенны, которая тратится на излучение. Вообще-то есть термин «потери на излучение» и это полезные «потери», если мы говорим об антенне, но это не равно сопротивлению излучения, так что не путайте. Нет никакого воображаемого сопротивления среды воображаемому излучению в нее или что либо еще — есть разные свойства вроде диэлектрической проницаемости, которые мы рассматривать пока что не будем.
Еще в антенне есть сопротивление потерь в виде сопротивления проводника, которое тратится на его нагрев, различные потери в конструктивных элементах и согласующих звеньях. Знание сопротивления излучения необходимо для понимания КПД антенны: у некоторых антенн сопротивление излучения может составлять единицы и доли Ома при том, что сопротивление потерь в разы больше, что значит что КПД такой антенны крайне низок несмотря на то, что в остальном ее конструкция адекватна. В простых антеннах вроде рассматриваемого диполя или граундплейна, сопротивление излучения близко к полному сопротивлению самой антенны, потому что потери в проводнике сравнительно малы, но в любом случае это не тождественные понятия.
Вернемся к диполю. Пока мы подаем энергию в его геометрическом центре, где ток максимален, а напряжение минимально, сопротивление излучения невелико. Теоретически оно равно приблизительно 73 Омам, а практически немного меньше в зависимости от относительной толщины материала. По мере расщепления одной из половин диполя на отдельные радиалы, сопротивление будет немного снижаться и упадет до приблизительно 36 Ом ми угле в 90° к штырю. Это очевидно влияет на КПД антенны. Но, для наглядности, будем рассматривать именно диполь. По мере смещения точки питания от центра к краю мы увидим, что ток падает, а напряжение растет, то есть растет сопротивление излучения, которое достигнет своего максимума при питании с конца. На все остальные характеристики антенны это обстоятельство не влияет, она по-прежнему излучает с той же диаграммой направленности, а значит, имеет ту же эффективность излучения (но не КПД всей антенны в сборе, потому что КПД зависит от относительных потерь).
Полное сопротивление антенны равно напряжению в точке питания, деленному на отдаваемый ток. А состоит оно из, как мы уже выяснили, сопротивления излучения, на котором мы полезно теряем энергию на нужное нам излучение, и сопротивления потерь, на котором мы теряем энергию бесполезно. Разными способами мы можем влиять на полное сопротивление антенны. Не меняя геометрию, мы можем смещать точку питания. Мы можем использовать различные трансформирующие элементы (включая буквально трансформаторы с обмотками на тех частотах, на которых их применение рационально). На эффективность излучения антенны все эти манипуляции никак не влияют и нужны только для согласования антенны с генератором (передатчиком). Например, полуволновый диполь с питанием по центру, сопротивление которого составляет приблизительно 73 Ома, через простой трансформатор 1:4 может быть согласованным с генератором, рассчитанным на антенну сопротивлением 18 Ом или 300 Ом — смотря как подключить выводы. На работе антенны это не скажется никак, кроме влияния потерь в трансформаторе на КПД всей конструкции в сборе.
Если вам кажется, что у антенны есть только монополь – некий штырь, кусок провода или просто дорожка на печатной плате, то на самом деле это вариант граундплейна, у которого нет специально выделенных радиалов, но радиалами служит земля, тело оператора (портативной радиостанции, например) или земляные полигоны на плате. Потери в таких радиалах очевидно больше, чем в специально созданных как часть антенны, поэтому КПД таких конструкций всегда ниже, равно как и степень согласования импедансов из-за непредсказуемости ситуативных вместо расчетных радиалов.
При увеличении длины антенны сверх полуволнового диполя сопротивление излучения сначала растет, достигая максимума при четном числе полуволн, а затем снова падает, достигая минимума при нечетном числе полуволн. Незначительное увеличение длины сужает диаграмму направленности и увеличивает эффективность передачи в выбранном направлении, а значительное приводит к дроблению диаграммы на множество лепестков и в целом неэффективно, поэтому на практике обычно не применяется кроме многодиапазонных антенн, в которых это является компромиссным решением.
Вообще любое увеличение длины диполя сверх половины волны приводит к тому, что на полотне возникают области, где ток течет в противоположном направлении. Этот ток, разумеется, также участвует в излучении, но интерференция создаваемого им поля с полем условно-основной части полотна и приводит к тому, что диаграмма направленности расщепляется, что в большинстве случаев вредно: обычно радиосвязь производится по одному или нескольким известным направлениям а излучение в «ненужную» сторону означает просто напрасные потери. Например, наземная связь проводится в направлении горизонта, а излучение в космос бесполезно тратит мощность передатчика. Поэтому, когда необходимо увеличить направленность антенны, чтобы посылать энергию более сфокусировано в нужном направлении, предпочитают использовать более сложные конструкции на базе диполя, а не удлиняют единичный диполь.
При уменьшении длины антенны от полуволнового диполя (или укорочению штыря четвертьволнового граундплейна) сопротивление излучения экспоненциально падает, что вкупе со все усложняющимся согласующим устройством делает укороченную антенну крайне неэффективной – небольшое сопротивление излучения рядом с большим сопротивлением означает напрасный нагрев согласующего устройства с малым излучением.
Вот, собственно, и все, что нужно знать гуманитарию об антеннах.