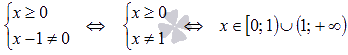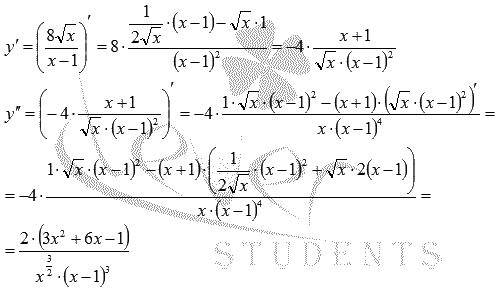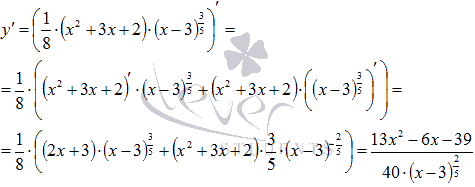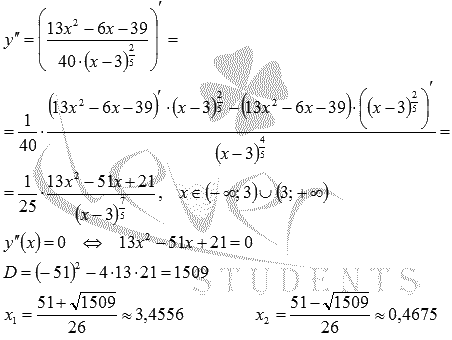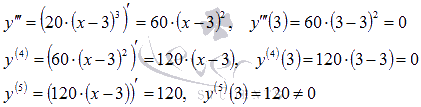Что такое выпуклость и вогнутость

Выпуклость и вогнутость графика функции

Содержание:

Выпуклость и вогнутость графика функции с точками перегиба

При исследовании функций с целью построения их графиков важную роль играют такие понятия как выпуклость и вогнутость кривых.

Определение 1. Кривая y = f (x) называется выпуклой в точке , если в окрестности этой точки кривая находится под касательной к кривой, проведенной в этой точке (рис.12).

Определение 2. Кривая y = f (x) называется вогнутой в точке, если в окрестности этой точки кривая находится над касательной к кривой, проведенной в этой точке (рис 13).

Определение 3. Кривая y = f (x) называется выпуклой (вогнутой) на промежутке (a, b), если она выпуклая (вогнутая) в каждой точке этого промежутка.

Для установления промежутков, на каких график функции y = f (x) выпуклый, а на каких вогнутый, укажем теорему, которая дает достаточные условия выпуклости и вогнутости кривых на промежутке.

ТЕОРЕМА. Если на промежутке (a, b) вторая производная функции y = f (x) отрицательна, то ее график выпуклый на этом промежутке, если f » (x) положительная на (a, b), то график y = f (x) вогнутый.

Не приводя строгого доказательства, приведем геометрические соображения, которые объясняют теорему.

Если везде на промежутке (a, b) то это означает, что f ‘(x), как функция, для которой f «(x) является производной, будет убывающей. Значит, убывает в рассматриваемом промежутке угловой коэффициент касательной к кривой и убывает сам угол , образуемый касательной с положительным направлением оси Ox (рис. 12).

Очевидно кривая на промежутке (a, b) расположена под касательной. Если, то кривая будет вогнутой.

Определение 4. Точка, отделяющая выпуклую часть непрерывной кривой от вогнутой, или наоборот, называется точкой перегиба.

Необходимые условия существования точки перегиба дает теорема.

ТЕОРЕМА. Если — точка перегиба непрерывной функции y = f (x), то вторая производная ее f» (x) в этой точке равна нулю или не существует.

Точки, в которых f» (x) равна нулю или не существует, называют критическими точками
второго рода.

Рис. 14.

Достаточно условия существования точки перегиба

ТЕОРЕМА. Если вторая производная f» (x) в точке равна нулю и меняет знак при переходе через эту точку, то точка с абсциссой является точкой перегиба кривой y = f (x).

Доказательство. Предположим, что в точке М с абсциссой вторая производная и при переходе через нее слева направо меняет знак с минуса на плюс. Тогда слева от М кривая выпуклая а справа кривая вогнутая Таким образом, в точке кривая меняет выпуклость на вогнутость, и поэтому точка М является точкой перегиба.

Пример. Найти точки перегиба и определить промежутки выпуклости и вогнутости кривой (кривая Гаусса).
Находим производные:
Приравниваем вторую производную к нулю и находим критические точки второго рода:

Эти точки разбивают область определения функции на промежутки (рис. 15). Находим знаки второй производной в этих промежутках.

Рис. 15. Рис. 16.

Итак, точки являются точками перегиба. На промежутке (-1; 1) кривая выпуклая, на промежутках кривая вогнутая (рис. 16).

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Что такое выпуклость и вогнутость

График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.

График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.

На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c).

Рассмотрим достаточный признак, позволяющий установить, будет ли график функции в данном интервале выпуклым или вогнутым.

Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f »(x) 0 – вогнутый.

Доказательство. Предположим для определенности, что f»(x) Î (a; b) и проведем через точку M₀ касательную. Ее уравнение . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной.

Итак, уравнение кривой имеет вид y = f(x). Обозначим ординату касательной, соответствующую абсциссе x. Тогда . Следовательно, разность ординат кривой и касательной при одном и том же значении x будет .

Разность f(x) – f(x₀) преобразуем по теореме Лагранжа , где c между x и x₀.

.

Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.

Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.

Определим достаточные условия того, что данная точка кривой является точкой перегиба.

Теорема. Пусть кривая определяется уравнением y = f(x). Если f »(x₀) = 0 или f »(x₀) не существует и при переходе через значение x = x₀ производная f »(x) меняет знак, то точка графика функции с абсциссой x = x₀ есть точка перегиба.

Доказательство. Пусть f »(x) 0 при x > x₀. Тогда при x x₀ – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x₀ есть точка перегиба. Аналогично можно рассматривать второй случай, когда f »(x) > 0 при x x₀.

Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.

Примеры. Найти точки перегиба и определить интервалы выпуклости и вогнутости кривых.

Найдем производные заданной функции до второго порядка.

.

. Вторая производная не существует при x = 1. Исследуем эту точку на возможный перегиб.

Итак, точка перегиба x = 1. Функция выпукла на (1; +∞), вогнута на (–∞; 1).

Возможные точки перегиба найдем, решив уравнение 2x 2 – 1 = 0. Отсюда .

Точки перегиба . Функция выпукла на и вогнута на .

.

при всех x из (–1; 1).

Следовательно, f(x) выпуклая на (–1; 1).

АСИМПТОТЫ ГРАФИКА ФУНКЦИИ

При исследовании функции важно установить форму ее графика при неограниченном удалении точки графика от начала координат.

Особый интерес представляет случай, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой.

Прямая называется асимптотой графика функции y = f(x), если расстояние от переменной точки M графика до этой прямой при удалении точки M в бесконечность стремится к нулю, т.е. точка графика функции при своем стремлении в бесконечность должна неограниченно приближаться к асимптоте.

Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее или с разных сторон, бесконечное множество раз пересекая асимптоту и переходя с одной ее стороны на другую.

Если обозначим через d расстояние от точки M кривой до асимптоты, то ясно, что d стремится к нулю при удалении точки M в бесконечность.

Будем в дальнейшем различать асимптоты вертикальные и наклонные.

Пусть при x→ x₀ с какой-либо стороны функция y = f(x)неограниченно возрастает по абсолютной величине, т.е. или или . Тогда из определения асимптоты следует, что прямая x = x₀ является асимптотой. Очевидно и обратное, если прямая x = x₀ является асимптотой, т. о. .

Таким образом, вертикальной асимптотой графика функции y = f(x) называется прямая, если f(x) → ∞ хотя бы при одном из условий x→ x₀ – 0 или x → x₀ + 0, x = x₀

Следовательно, для отыскания вертикальных асимптот графика функции y = f(x) нужно найти те значения x = x₀, при которых функция обращается в бесконечность (терпит бесконечный разрыв). Тогда вертикальная асимптота имеет уравнение x = x₀.

Так как , то прямая x = 2 является вертикальной асимптотой.

Прямая x = 0 – вертикальная асимптота.

Поскольку асимптота – это прямая, то если кривая y = f(x) имеет наклонную асимптоту, то ее уравнение будет y = kx + b. Наша задача найти коэффициенты k и b.

Теорема. Прямая y = kx + b служит наклонной асимптотой при x → +∞ для графика функции y = f(x) тогда и только тогда, когда . Аналогичное утверждение верно и при x → –∞.

Доказательство. Пусть MP – длина отрезка, равного расстоянию от точки M до асимптоты. По условию . Обозначим через φ угол наклона асимптоты к оси Ox. Тогда из ΔMNP следует, что . Так как φ постоянный угол (φ ≠ π/2), то , но

Следовательно, мы можем записать следующее равенство .

Так как x → +∞, то должно выполняться равенство . Но при постоянных k и b и . Следовательно, , т.е. .

Если число k уже известно, то , поэтому .

Для доказательства в случае x → –∞ все рассуждения аналогичны.

Докажем обратное утверждение. Предположим, что существуют пределы, определяющие числа k и b. Тогда несложно заметить, что выполняется равенство . Действительно

Следовательно, прямая y = kx + b есть асимптота. Теорема полностью доказана.

Сделаем несколько замечаний.

Замечание 1. Теорема показывает, что для нахождения асимптот достаточно найти два указанных предела. Причем, если хотя бы один из пределов не существует или обращается в бесконечность, то кривая асимптот не имеет.

Замечание 2. В случае, когда k = 0 асимптота y = b называется горизонтальной асимптотой. Наличие горизонтальной асимптоты означает, что существуют пределы

.

Замечание 3. Пределы для отыскания k и b могут быть различны при x → +∞ и x → – ∞ и, следовательно, график функции может иметь две различные асимптоты при x → +∞ и x → –∞.

Примеры. Найти асимптоты кривых.

x = 0 – вертикальная асимптота.

.

а) .

Итак, при x → +∞ наклонная асимптота у= х.

б) , т. к.

а) .

. Наклонная асимптота y = x – π при .

б) при .

Источник

Выпуклость функции. Направление выпуклости. Точки перегиба. Условия выпуклости и перегиба.

При исследовании функции и построении ее графика на одном из этапов мы определяем точки перегиба и интервалы выпуклости. Эти данные вместе с промежутками возрастания и убывания позволяют схематично представить график исследуемой функции.

Дальнейшее изложение подразумевает, что Вы умеете находить производные функции до некоторого порядка и решать неравенства разных видов.

Изучение материала начнем с необходимых определений и понятий. Далее озвучим связь между значением второй производной функции на некотором интервале и направлением ее выпуклости. После этого перейдем к условиям, которые позводляют определять точки перегиба графика функции. По тексту будем приводить характерные примеры с подробными решениями.

Навигация по странице.

Выпуклость, вогнутость функции, точка перегиба.

Выпуклую вверх функцию часто называют выпуклой, а выпуклую вниз – вогнутой.

Посмотрите на чертеж, иллюстрирующий эти определения.

Другими словами, точка М называется точкой перегиба графика функции, если в этой точке существует касательная и график функции меняет направление выпуклости, проходя через нее.

Если необходимо, обратитесь к разделу касательная к графику функции в точке, чтобы вспомнить условия существования невертикальной и вертикальной касательной.

На рисунке ниже представлены несколько примеров точек перегиба (отмечены красными точками). Заметим, что некоторые функции могут не иметь точек перегиба, а другие могут иметь одну, несколько или бесконечно много точек перегиба.

Нахождение интервалов выпуклости функции.

Сформулируем теорему, которая позволяет определять промежутки выпуклости функции.

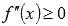
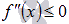
Эта теорема позволяет находитьть промежутки вогнутости и выпуклости функции, нужно лишь на области определения исходной функции решить неравенства и соответственно.

Следует отметить, что точки, в которых функция y=f(x) определена, а вторая производная не существует, будем включать в интервалы вогнутости и выпуклости.

Разберемся с этим на примере.

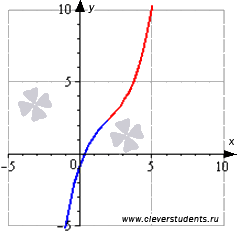
Выяснить промежутки, на которых график функции 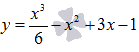имеет выпуклость направленную вверх и выпуклость направленную вниз.

Область определения функции 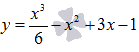— это все множество действительных чисел.

Найдем вторую производную.

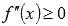
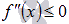
Область определения второй производной совпадает с областью определения исходной функции, поэтому, чтобы выяснить интервалы вогнутости и выпуклости, достаточно решить и соответственно.

Следовательно, функция выпуклая вниз на интервале и выпуклая вверх на интервале .

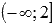
Часть графика функции на интервале выпуклости изображена синим цветом, на интервале вогнутости – красным цветом.

Сейчас рассмотрим пример, когда область определения второй производной не совпадает с областью определения функции. В этом случае, как мы уже отмечали, точки области определения, в которых не существует конечная вторая производная, следует включать в интервалы выпуклости и (или) вогнутости.

Найти промежутки выпуклости и вогнутости графика функции .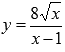

Начнем с области определения функции:

Найдем вторую производную:

Областью определения второй производной является множество 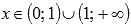. Как видите, x=0 принадлежит области определения исходной функции, но не принадлежит области определения второй производной. Не забывайте про эту точку, ее нужно будет включить в интервал выпуклости и (или) вогнутости.

Таким образом,

и

При график функции имеет выпуклость направленную вниз, при — выпуклость направленную вверх.

Часть графика функции на интервале выпуклости изображена синим цветом, на интервалах вогнутости – красным цветом, черной пунктирной прямой является вертикальная асимптота.

Необходимое и достаточные условия перегиба.

Необходимое условие перегиба.

Сформулируем необходимое условие перегиба графика функции.

Пусть график функции y=f(x) имеет перегиб в точке и имеет при непрерывную вторую производную, тогда выполняется равенство .

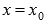
Из этого условия следует, что абсциссы точек перегиба следует искать среди тех, в которых вторая производная функции обращается в ноль. НО, это условие не является достаточным, то есть не все значения , в которых вторая производная равна нулю, являются абсциссами точек перегиба.

Еще следует обратить внимание, что по определению точки перегиба требуется существование касательной прямой, можно и вертикальной. Что это означает? А означает это следующее: абсциссами точек перегиба могут быть все из области определения функции, для которых и . Обычно это точки, в которых знаменатель первой производной обращается в ноль.

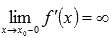
Первое достаточное условие перегиба.

После того как найдены все , которые могут быть абсциссами точек перегиба, следует воспользоваться первым достаточным условием перегиба графика функции.

Пусть функция y=f(x) непрерывна в точке , имеет в ней касательную (можно вертикальную) и эта функция имеет вторую производную в некоторой окрестности точки . Тогда, если в пределах этой окрестности слева и справа от , вторая производная имеет разные знаки, то является точкой перегиба графика функции.

Как видите первое достаточное условие не требует существования второй производной в самой точке , но требует ее существование в окрестности точки .

Сейчас обобщим всю информацию в виде алгоритма.

Алгоритм нахождения точек перегиба функции.

Находим все абсциссы возможных точек перегиба графика функции ( или и ) и выясняем, проходя через какие вторая производная меняет знак. Такие значения и будут абсциссами точек перегиба, а соответствующие им точки будут точками перегиба графика функции.

Рассмотрим два примера нахождения точек перегиба для разъяснения.

Найти точки перегиба и интервалы выпуклости и вогнутости графика функции .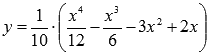

Областью определения функции является все множество действительных чисел.

Найдем первую производную:

Областью определения первой производной также является все множество действительных чисел, поэтому равенства и не выполняется ни для каких .

Найдем вторую производную:

Выясним при каких значениях аргумента x вторая производная обращается в ноль:

Теперь осталось проверить по достаточному признаку перегиба, в каких из этих точек вторая производная меняет знак. Для этого нанесем точки x=-2 и x=3 на числовую ось и, как в обобщенном методе интервалов, расставим знаки второй производной над каждым промежутком. Под каждым интервалом схематично дугами показано направление выпуклости графика функции.

Взглянув еще раз на числовую ось и знаки второй производной на ее промежутках, можно делать вывод об интервалах выпуклости и вогнутости. График функции выпуклый на интервале 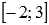и вогнутый на интервалах и .

Часть графика функции на интервале выпуклости изображена синим цветом, на интервалах вогнутости – красным цветом, точки перегиба показаны черными точками.

Найдите абсциссы всех точек перегиба графика функции .

Областью определения данной функции является все множество действительных чисел.

Найдем производную.

Находим вторую производную, область ее определения и точки, в которых она обращается в ноль:

Получили еще две возможные абсциссы точек перегиба. Отмечаем все три точки на числовой прямой и определяем знак второй производной на каждом из полученных интервалов.

Вторая производная меняет знак, проходя через каждую из точек, следовательно, все они являются абсциссами точек перегиба.

Части графика функции на интервалах выпуклости изображены синим цветом, на интервалах вогнутости – красным цветом, точки перегиба показаны черными точками.

Первое достаточное условие перегиба графика функции позволяет определять точки перегиба и не требуют существования второй производной в них. Поэтому, первое достаточное условие можно считать универсальным и самым используемым.

Сейчас сформулируем еще два достаточных условия перегиба, но они применимы лишь при существовании конечной производной в точке перегиба до некоторого порядка.

Второе достаточное условие перегиба.

Выяснить, является ли точка 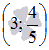точкой перегиба графика функции .

Для начала убедимся, что точка 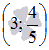принадлежит графику функции:

Функция определена для всех действительных значений аргумента. Найдем первую и вторую производные.

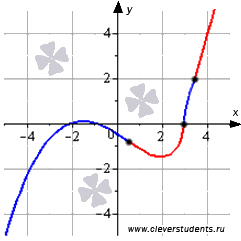
Часть графика функции на интервале выпуклости изображена синим цветом, на интервале вогнутости – красным цветом, точка перегиба показана черной точкой.

Третье достаточное условие перегиба.

Найдите точки перегиба графика функции .

Функция определена на всем множестве действительных чисел.

Таким образом, в точке с абсциссой x=3 может быть перегиб графика функции. Чтобы убедиться в том, что х=3 действительно абсцисса точки перегиба, воспользуемся третьим достаточным условием.

Часть графика функции на интервале выпуклости изображена синим цветом, на интервале вогнутости – красным цветом, точка перегиба показана черной точкой.

Источник