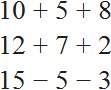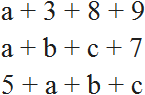Что такое вырази в математике
Что такое числовые выражения
Содержание статьи
Отличительной особенностью выражения является наличие математических действий. Оно обозначаются определенными знаками (умножения, деления, вычитания или сложения). Последовательность выполнения математических действий при необходимости корректируется скобками. Выполнить математические действия – значит найти значение выражения.
Что не является выражением
Не всякую математическую запись можно отнести к числу выражений.
Равенства не являются выражениями. Присутствуют при этом в равенстве математические действия или нет, не имеет значения. Например, a=5 – это равенство, а не выражение, но и 8+6*2=20 тоже нельзя считать выражением, хотя в нем и присутствуют умножение и сложение. Этот пример тоже принадлежит к категории равенств.
Понятия выражения и равенства не являются взаимоисключающими, первое входят в состав второго. Знак равенства соединяет два выражения:
5+7=24:2
Можно это равенство упростить:
5+7=12
Выражение всегда предполагает, что представленные в нем математические действия могут быть выполнены. 9+:-7 – это не выражение, хотя здесь есть знаки математических действий, ведь выполнить эти действия невозможно.
Существуют и такие математические примеры, которые формально являются выражениями, но не имеют смысла. Пример такого выражения:
46:(5-2-3)
Число 46 необходимо разделить на результат действий в скобках, а он равен нулю. На нуль же делить нельзя, такое действие в математике считается запретным.
Числовые и алгебраические выражения
Существует два вида математических выражений.
Если выражение содержит только числа и знаки математических действий, такое выражение называется числовым. Если же в выражении наряду с числами присутствуют переменные, обозначаемые буквами, или чисел нет вообще, выражение состоит только из переменных и знаков математических действий, оно называется алгебраическим.
Принципиальное отличие числового значения от алгебраического состоит в том, что у числового выражения значение только одно. Например, значение числового выражения 56–2*3 всегда будет равно 50, ничего изменить нельзя. У алгебраического же выражения значений может быть много, ведь вместо буквы можно подставить любое число. Так, если в выражении b–7 вместо b подставить 9, значение выражения будет равно 2, а если 200 – оно будет составлять 193.
Числовые и буквенные выражения
Числовые выражения
В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.
Значение выражения — это результат выполненных действий.
Чтение числовых выражений
Решение числовых выражений
45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13
Сравнение значений числовых выражений
Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.
Для этого найдем значения каждого из них:
Буквенные выражения
Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.
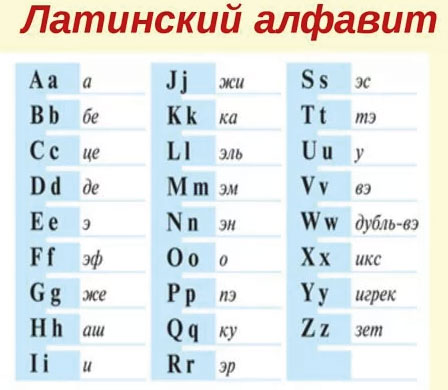
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.
Чаще всего используются буквы:
a, b, c, d, x, y, k, m, n
Алгоритм решения буквенного выражения
1. Прочитать буквенное выражение
2. Записать буквенное выражение
3. Подставить значение неизвестного в выражении
4. Вычислить результат
Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с
Подставим вместо неизвестного «с» число 4.
У нас получается выражение: 28 – 4
Переменные
Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства
Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:
Теперь мы можем найти значение этого выражения:
с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7
Поделись с друзьями в социальных сетях:
Числовые и буквенные выражения. Формулы
Так же, как и у нашего языка общения есть алфавит и знаки-помощники (точка, тире, запятая и т.д.), математический язык вычисления также имеет свой алфавит:
Буквы и цифры в математике служат для обозначения чисел.
Цифрами обозначается конкретное, какое-то определённое число.
Буквами – любое или неизвестное число, в зависимости от задачи.
МАТЕМАТИЧЕСКИЕ ВЫРАЖЕНИЯ – это «слова» и «фразы» математики, записи, в которых содержатся:
При этом знаки математических действий и вспомогательные знаки ОБЯЗАТЕЛЬНО связывают числа и обозначают последовательность действий над ними.
Примеры математических выражений:
ВНИМАНИЕ!
НЕ ЯВЛЯЕТСЯ математическим выражением:
Например, это НЕ математические выражения:
Случаи опускания знака умножения в выражениях
В буквенных выражениях обычно знак умножения пишут только между числами, которые выражены цифрами.
В остальных случаях знак умножения опускают, например:
Как читать математические выражения
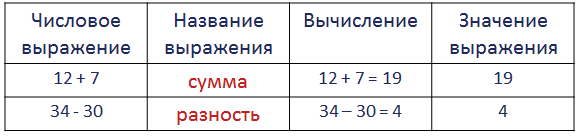
Простейшие математические выражения, состоящие из одного математического действия, называются по названию результата этого действия:
Более сложные выражения, называют по последнему выполняемому действию:
Важно не только уметь читать готовые математические выражения, но и «переводить» слова на математический язык – язык чисел, знаков действия и других символов:
Алгоритм чтения математических выражений
Чтобы прочитать математическое выражение, нужно:
При чтении сложного выражения повторяем действия алгоритма столько раз, сколько необходимо.
Формулы
Используя математические выражения можно одну величину представить в виде другой, то есть, установить зависимость значения одной величины от значения другой величины.
Велосипедист едет со скоростью \(v_<1>\) км/ч. Найти скорость:
а) автомобиля, если известно, что он едет в 3 раза быстрее: \(v_=3\cdot v_<1>\);
б) пешехода, если известно, что он двигается на 15 км/ч медленнее: \(v_
= v_<1>-15\).
Иначе это называется выразить одну величину через другую.
Многие величины в математике имеют свои собственные обозначения. Например: S – площадь фигуры, P – периметр, t – время и т.д.
Запись такого равенства называется формулой.
ФОРМУЛА – это запись зависимости значения некоторой величины от значений одной или нескольких других величин. Или другими словами, это запись правила вычисления одной неизвестной величины при помощи известных других.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.3 / 5. Количество оценок: 8
Выражения
Выражение — это любое сочетание чисел, букв и знаков операций. Можно сказать, что вся математика состоит из выражений.
Выражения бывают двух видов: числовые и буквенные.
Числовые выражения состоят из чисел и знаков математических операций. Например, следующие выражения являются числовыми:
Буквенные выражения помимо чисел и знаков операций содержат ещё и буквы. Например, следующие выражения являются буквенными:
Буквы, которые содержатся в буквенных выражениях, называются переменными. Запомните это раз и навсегда! Спросите любого школьника что такое переменная — этот вопрос поставит его в ступор, несмотря на то что он будет решать сложные задачи по математике, не зная что это такое. А между тем, переменная это фундаментальное понятие, без понимания которого математику невозможно изучать.
Под словом «изучать» мы подразумеваем самостоятельное чтение соответствующей литературы и способность понимать, что там написано. А то вроде и знаешь математику на четвёрку, задачи решаешь, но не можешь понять, что написано в лекциях и книгах. Каждому знакомо такое чувство, особенно студентам.
Поскольку понятие переменной очень важно, остановимся на нём подробнее. Посмотрите внимательно на слово «переменная». Ничего не напоминает? Слово «переменная» происходит от слов «меняться», «изменить», «изменить своё значение». Переменная в математике всегда выражена какой-то буквой. Например, запишем следующее выражение:
Значение переменной a подставляется в исходное выражение.
В результате имеем: 5 + 5 = 10
Конечно, мы рассмотрели простейшее выражение. На практике встречаются более сложные выражения, в которых присутствуют дроби, степени, корни и скобки. Выглядит это устрашающе. На самом деле ничего страшного. Главное понять сам принцип.
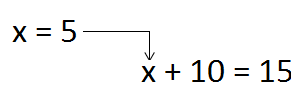
Переменная это своего рода контейнер, где хранится значение. Переменные удобны тем, что они позволяют, не приводя примеров доказывать теоремы, записывать различные формулы и законы.
Имея выражение a + b = c, можно пользоваться им, подставляя вместо переменных a и b любые числа. А переменная c будет получать своё значение автоматически, в зависимости от того, какие числа будут подставлены вместо a и b
Решение:
Значение выражения
Фраза « выполнить действие » означает выполнить одну из операций действия.
Значение выражения — это результат выполнения действий, содержащихся в выражении.
Рассмотрим еще примеры:
Урок математике по теме: «Выражения»
Разделы: Математика
Цели: уточнить понятие «выражение», «числовое выражение», «буквенное выражение». Тренировать способность к составлению сумм и разностей по тексту задач, нахождению значений числовых и буквенных выражений. Формировать способность к использованию скобок для обозначения порядка действий в выражениях; тренировать вычислительные навыки к счёту через 5.
II. Актуализация знаний
— Как называют в математике такую запись? (Выражение)
— Найдите значение выражения. (102)
— Выразите 102 в разных единицах счёта.
— Выразите 102 см в различных единицах длины.
102 см 5 дм 4 см 1 м 2 см 21 дм
___. Определение темы урока
1. Решить примеры, расположить ответы в порядке возрастания, прочитать слово.
— Что такое выражение? Рассмотрите записи на доске и дайте определение?
— На какие две группы можно разделить данные выражения?
— Как можно назвать первую группу выражений? (числовые)
— Вторую группу выражений? (буквенные)
_V. Открытие нового
Составьте к данным карточкам задачи: (устно)
— К каким карточкам вам не удалось составить задачу?
(Вывод: записи, в которых есть знаки сравнения, не являются выражениями)
V. Первичное закрепление (Приложение 1)
1. Определите, являются ли выражениями, данные записи?
Мы зарядку начинаем,
Наши руки разминаем,
Разминаем спину, плечи,
Чтоб сидеть нам было легче.
Дружно прыгаем, прыг-скок!
Кто достанет потолок?
А теперь ходьба на месте.
Громко топаем все вместе.
Мы закончили зарядку,
Возвращаемся к тетрадкам.
3. Запишите выражения к следующим задачам в тетради
Саша заплатил за чай а руб., а за булочку b руб. Сколько всего денег заплатил Саша?
— Что мы записали? (выражения)
— Какие выражения мы записали? (числовое, буквенное)
— В каком выражении мы сможем найти результат? (в числовом)
Вывод: выполнив действие в числовом выражении, найдём значение выражения.
Найдите, какие из данных выражений имеют одинаковое значение?
— Что нового узнали? Какое открытие сделали?