Что такое высказывание в алгебре логики
Общие теоретические сведения
Основные понятия алгебры логики
Логической основой компьютера является алгебра логики, которая рассматривает логические операции над высказываниями.
Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.
Пример. «3 – простое число» является высказыванием, поскольку оно истинно.
Не всякое предложение является логическим высказыванием.
Пример. предложение «Давайте пойдем в кино» не является высказыванием. Вопросительные и побудительные предложения высказываниями не являются.
Высказывательная форма – это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.
Алгебра логики рассматривает любое высказывание только с одной точки зрения – является ли оно истинным или ложным. Слова и словосочетания «не», «и», «или», «если. то», «тогда и только тогда» и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.
Высказывания, образованные из других высказываний с помощью логических связок, называются составными (сложными). Высказывания, которые не являются составными, называются элементарными (простыми).
Истинность или ложность составных высказываний зависит от истинности или ложности элементарных высказываний, из которых они состоят.
Чтобы обращаться к логическим высказываниям, им назначают имена.
Пример. Обозначим через А простое высказывание «число 6 делится на 2», а через В простое высказывание «число 6 делится на 3». Тогда составное высказывание «Число 6 делится на 2, и число 6 делится на 3» можно записать как «А и В». Здесь «и» – логическая связка, А, В – логические переменные, которые могут принимать только два значения – «истина» или «ложь», обозначаемые, соответственно, «1» и «0».
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение (табл. 1).
Таблица 1. Основные логические операции
Конъюнкция (логическое умножение)
Дизъюнкция (логическое сложение)
Тогда и только тогда
Исключающее ИЛИ (сложение по модулю 2)
НЕ Операция, выражаемая словом «не», называется отрицанием и обозначается чертой над высказыванием (или знаком ). Высказывание А истинно, когда A ложно, и ложно, когда A истинно.
Пример. Пусть А=«Сегодня пасмурно», тогда А=«Сегодня не пасмурно».
И Операция, выражаемая связкой «и», называется конъюнкцией (лат. conjunctio – соединение) или логическим умножением и обозначается точкой « • » (может также обозначаться знаками или &). Высказывание А • В истинно тогда и только тогда, когда оба высказывания А и В истинны.
ИЛИ Операция, выражаемая связкой «или» (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio – разделение) или логическим сложением.
Пример. Высказывание «если студент сдал все экзамены на «отлично», то он получит стипендию». Очевидно, эту импликацию следует признать ложной лишь в том случае, когда студент сдал на «отлично» все экзамены, но стипендии не получил. В остальных случаях, когда не все экзамены сданы на «отлично» и стипендия получена (например, в силу того, что студент проживает в малообеспеченной семье) либо когда экзамены вообще не сданы и о стипендии не может быть и речи, импликацию можно признать истинной.
РАВНОСИЛЬНО Операция, выражаемая связками «тогда и только тогда», «необходимо и достаточно», «. равносильно …», называется эквиваленцией или двойной импликацией и обозначается знаком ↔ или
. Высказывание А↔В истинно тогда и только тогда, когда значения А и В совпадают.
Пример. Высказывание «Число 6 либо нечетно либо делится без остатка на 2» является истинным, а высказывание «Либо число 6 четно либо число 6 делится на 3» – ложно, так как истинны оба высказывания входящие в него.
Вывод. Операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания.
Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания («не»), затем конъюнкция («и»), после конъюнкции – дизъюнкция («или») и исключающего или и в последнюю очередь – импликация и эквиваленция.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).
Значения логической функции для разных сочетаний значений входных переменных – или, как это иначе называют, наборов входных переменных – обычно задаются специальной таблицей. Такая таблица называется таблицей истинности.
Алгоритм построения таблиц истинности для сложных выражений:
Примечание: И–НЕ называют также «штрих Шеффера» (обозначают | ) или «антиконъюнкция»; ИЛИ–НЕ называют также «стрелка Пирса» (обозначают ↓) или «антидизъюнкция».
Существует три базовых логических элемента, которые реализуют три основные логические операции:
Поскольку любая логическая операция может быть представлена в виде комбинации трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов, как из “кирпичиков”.
Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс – логический смысл сигнала – 1, нет импульса – 0. На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции.
Преобразование сигнала логическим элементом задается таблицей состояний, которая фактически является таблицей истинности, соответствующей логической функции, только представлена в форме логических схем. В такой форме удобно изображать цепочки логических операций и производить их вычисления.
Основы алгебры логики
Основные понятия и аксиомы алгебры логики. Простые и сложные высказывания.
Исследования в алгебре логики тесно связаны с изучением высказываний, вызвано это тем, что высказывания являются одним из основных видов носителей информации. С помощью высказываний мы устанавливаем свойства, взаимосвязи между объектами.
Примерами высказываний на естественном языке являются предложения: « Сегодня светит солнце » или « На Красной площади зимой 2007–2008 гг. заливали каток ». Каждое из этих высказываний характеризует свойства или состояние конкретного объекта. Каждое высказывание несет значение « истина » или « ложь ».
Определение. Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности.
Это определение не является математически точным.
Более того, только на первый взгляд оно кажется удовлетворительным. Это определение породило много логических парадоксов.
Причина этого парадокса лежит в структуре построения указанного предложения : оно ссылается на свое собственное значение. С помощью определенных ограничений на допустимые формы высказываний могут быть устранены такие ссылки на себя, и, следовательно, устранены возникающие отсюда парадоксы.
Интересную задачу, содержащую парадокс, придумал знаменитый математик « Известно, что в некотором городе брадобрей бреет всех тех и только тех жителей города, которые не бреются сами. Кто бреет брадобрея? »
Определение. Высказывание называется простым (элементарным), если никакая его часть сама не является высказыванием.
Алгебра логики отвлекается от смысловой содержательности высказываний. Мы можем договориться, что абсурдное по смыслу высказывание: « Крокодилы летают » – является истинным, и с этим значением высказывания будем работать.
Введение таких ограничений дает возможность изучать высказывания алгебраическими методами, т.е. позволяет ввести операции над элементарными высказываниями и с их помощью строить и изучать составные высказывания.
Употребляемые в русском языке связки « и », « или », « не », « если…, то… », « тогда и только тогда, когда … » позволяют из уже заданных высказываний строить новые, более « сложные » высказывания.
Определение. Сложное высказывание – это высказывание, которое состоит из двух или более простых высказываний, объединенных логическими связками.
В алгебре логики логическая операция полностью задается таблицей истинности, указывающей, какие значения принимает сложное высказывание при всех возможных значениях простых высказываний, входящих в сложное высказывание.
Логические операции и соответствующие им логические связки имеют специальные названия и обозначаются следующим образом:
Конспект по элементам математической логики на тему «Высказывания в алгебре логики и логические операции над ними»
Высказывания в алгебре логики и логические операции над ними
Элементами логических рассуждений являются высказывания.
Простое высказывание – это повествовательное предложение, которое или истинно, или ложно.
Число 100 делится на 25 без остатка (истинно).
Рим – столица Франции (ложно).
Вопросительные и восклицательные предложения не являются высказываниями. Простые высказывания обозначаются заглавными буквами латинского алфавита.
Истинностными значениями высказываний являются значения «истина» и «ложь». Обозначается: «И», «Л». Используются также обозначения: 0 и 1.
Составные высказывания образуются путем соединения простых высказываний с помощью специальных связок «и», «или», «если…, то» и других связок. Эти связки называются логическими операциями над высказываниями. Логические операции строго и однозначно определены.
Действия логических операций задаются таблицами истинности.
Эти таблицы содержит все комбинации значений истинности простых высказываний, и для каждой такой комбинации указывается значение истинности сложного высказывания.
К основным логическим операциям над высказываниями относятся: отрицание, дизъюнкция, конъюнкция, импликация, сложение по модулю 2, эквивалентность, стрелка Пирса, штрих Шеффера.
Отрицание – высказывание, которое образуется с помощью союзов «не», «неверно, что…».
Например, «неверно, что пять больше десяти».
Когда высказывание А истинно, то 

Двойное отрицание 
Дизъюнкция (логическое сложение) – высказывание, которое образуется путем соединения простых высказываний с помощью союза «или» (неразделимое «или», «или» с включением союза «и»).
Алгебра логики
Алгебра логики — раздел математики, изучающий высказывания с точки зрения их логических значений (истинности или ложности) и логических операций над ними.
Иногда ее называют двоичной логикой или булевой алгеброй по имени английского математика Джорджа Буля.
Для удобства записи, используют обозначение результата через F, а логические высказывания через A (X) и B (Y). Так как возможных вариантов значений всего два, их можно обозначить через 0 (ложь, нет, false, no) и 1 (истина, да, true, yes).
Таблица истинности — табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.
Логическое высказывание
Логическое высказывание — любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.
Тождественно истинные высказывания (тавтология)
Тождественно истинными называются высказывания, истинные при любых значениях входящих в него переменных.
Таким образом, такое высказывание всегда равно 1.
В качестве примеров можно привести высказывания, являющиеся разъяснением термина на основе его словообразования (авиабаза — место базирования авиационной техники). Или любое сложное высказывание, смысл которого сводится к формуле А \/ ¬A.
Тождественно ложные высказывания
Тождественно ложными называются высказывания, ложные при любых значениях входящих в него переменных.
Таким образом, такое высказывание всегда равно 0.
Важно, что большинство высказываний сводится к формуле А /\ ¬A.
Эквивалентные высказывания
Эквивалентными (тождественными или равносильными) называются высказывания, значения которых совпадают при любых значениях входящих в него переменных.
Логические операции
Логическое умножение (конъюнкция)
Представляет собой объединение нескольких логических выражений с помощью союза И. При практическом наборе на компьютере часто используют знаки прямого и обратного деления без пробела: /\
Таким образом, все значения должны быть истинными: И первое, И второе, И. При умножении логических операторов мы получим единицу только если все они будут равны единице:
| A | B | F = A & B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Отсюда вытекает обратное следствие, упрощающее вычисления для конъюнкции:
Если хотя бы одно значение ложно, то ложно и всё выражение.
Логическое сложение (дизъюнкция)
Представляет собой объединение логических выражений с помощью союза ИЛИ. Если при сложении результат становится больше нуля, то он выражается единицей. При практическом наборе на компьютере часто используют знаки обратного и прямого деления без пробела: \/
| A | B | F = A \/ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Отсюда вытекает обратное следствие, упрощающее вычисления для дизъюнкции:
Если хотя бы одно значение истинно, то истинно и всё выражение.
Логическое отрицание (инверсия)
Представляет собой логическое выражение с добавленной в начале частицей НЕ. То есть операция всегда обращает значение в противоположное.
| A | F = ¬A |
| 0 | 1 |
| 1 | 0 |
Логическое следование (импликация)
Связывает два логических выражения с помощью оборота ЕСЛИ. ТО.
Дополнительная операция, так как A → B = 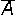
Кроме того, при построении высказывания могут использоваться выражения «из. следует», «. влечет».
| A | B | F = A → B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
В таблице хорошо видна практическая суть: импликация ложна только тогда, когда первое выражение истинно, а второе ложно.
При решении задач, в большинстве случаев требуется применение закона снятия импликации.
Логическое равенство (эквивалентность)
Образуется соединением двух логических выражений с помощью оборотов «тогда и только тогда», «необходимо и достаточно», «. равносильно. ». Поскольку мы видим здесь двойное следование (и вправо и влево), операцию иногда называют двойной импликацией. Дополнительная операция, так как A ↔ B = (A ∨ 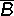
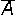
| A | B | F = A ↔ B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Суть: эквивалентность ложна только тогда, когда выражения разные.
Законы алгебры логики
Те, кому лень учить эти законы, должны вспомнить алгебру, где знание нескольких способов преобразования позволяет решать очень сложные уравнения.
Строго говоря, это не законы, а теоремы. Но их доказательство не входит в программу изучения. Впрочем, доказательство обычно основывается на построении полной таблицы истинности.
Замечание. Знаки алгебры логики намеренно заменены на сложение и умножение.
| № | Для ИЛИ | Для И | Примечание |
| 1 | A + 0 = A | A • 1 = A | Ничего не меняется при действии, константы удаляются |
| 2 | A + 1 = 1 | A • 0 = 0 | Удаляются переменные, так как их оценивание не имеет смысла |
| 3 | A + B = B + A | AB = BA | Переместительный (коммутативности) |
| 4 | A + 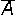 = 1 = 1 | Один из операторов всегда 1 (закон исключения третьего) | |
| 5 | A • 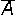 = 0 = 0 | Один из операторов всегда 0 (закон непротиворечия) | |
| 6 | A + A = A | A • A = A | Идемпотентности (NB! Вместо A можно подставить составное выражение!) |
| 7 | ¬¬A = A | Двойное отрицание | |
| 8 | (A+B)+C = A+( B+C) | (A•B)•C = A•(B•C) | Ассоциативный |
| 9 | (A+B)•C = = (A•C)+( B•C) | (A•B)+C = = (A+C)•( B+C) | Дистрибутивный |
| 10 | (A+B)•(¬A+B) = B | (A•B)+(¬A•B) = B | Склеивания |
| 11 | ¬(A+B) = ¬A•¬ B | ¬(A•B) = ¬A+¬ B | Правило де Моргана |
| 12 | A+(A•C) = A | A•(A+C) = A | Поглощение |
| 13 | A→B = ¬A+ B и A→B = ¬B→ ¬A | Снятие (замена) импликации | |
| 14 | 1) A↔B = (A•B)+(¬A•¬ B) 2) A↔B = (A + ¬B)•(¬A + B) | Снятие (замена) эквивалентности | |
Порядок решения логического выражения
В первую очередь надо учитывать, что порядок задается скобками.
Далее выполняются операции отрицания, конъюнкции, дизъюнкции, импликации, эквивалентности.
Построение таблиц истинности
Чтобы решить логическое выражение, необходимо построить таблицу истинности, описывающую ВСЕ возможные варианты значений переменных величин. В связи с тем, что мы используем булевы переменные (то есть имеющие только два значения: 0 и 1), количество вариантов легко сосчитать по формуле
где N — число переменных, а M — число строк в результирующей таблице.
Заполнение же значений фактически является последовательным вписыванием в каждой строке двоичных чисел. Для первой строки это будет 0 (00, 000. ), для второй — 1 (01, 001. ), а для последней — числа, состоящего из всех единиц. Выполнение этого несложного правила позволит не только избежать ошибок, но и облегчит решение, так как значения 0/1 будут подчиняться определенному порядку для каждой переменной.
Графическое решение числовых выражений по координатной прямой
Ряд заданий в алгебре логики основывается в использовании в качестве высказывания числового выражения. Например,
Хорошо видно, что выражение берется в скобки для однозначного восприятия. Прежде чем наносить значения на рисунок, следует избавиться от отрицания. В этом случае происходит замена знаков отношения на противоположные по схеме: ↔ ≤, = ↔ ≠.
В нашем примере мы получим
Нанесем два значения на координатную прямую и, учитывая логическое И, у нас должны совпасть оба условия. То есть на прямой это будет пересечение, обозначенное красным.
Возможные целочисленные ответы — 3, 4, 5.
Построение логического выражения по таблице истинности
Задача является противоположной стандартной.
При ее решении нужно построить дизъюнкцию для всех строк, равных 1, то есть составить выражение в дизъюнктивной нормальной форме (ДНФ).
Решение текстовых задач
На предыдущих этапах, в частности, изучались графический и табличный способы, которые невозможно, либо чрезмерно трудоемко использовать для сложных заданий. Также, решение задач путем рассуждений зачастую неэффективно.
Многие учащиеся очень расстраиваются, что, используя ранее эти способы, они тратили много времени на то, чтобы выработать стратегию, правильно понимать задание и т.п. А теперь их удается решить буквально за несколько секунд. Эта позиция неверна. Большинство подобных задач в реальной жизни не содержит достаточных сведений для решения средствами алгебры логики. Умение анализировать данные и находить «пробелы» в исходных данных — намного важнее.
При решении логической задачи средствами алгебры логики, необходимо выделить из текста логические условия и записать их в виде выражения.
Каждое высказывание оформляется в виде логической переменной. Чаще всего удобно вводить переменные, обозначенные русскими буквами и связанные с объектами, описанными в задаче: Иван — И, красный — К (или Кр, если переменная К уже введена для Коли) и т.п.
В большинстве случаев потребуется упрощение выражения с использованием законов алгебры логики.
В некоторых случаях удобно составить систему высказываний (аналогично системе уравнений) и, затем, решать уже её.
Логическое значение категорически рекомендуется записывать как 0 (ложь) или 1 (истина). Это поможет дифференцировать записи, а не спотыкаться о глупейшие варианты Л/И.
Введем обозначения для логических высказываний:
Л — победит Ласточка; С — победит Стрела; Т — победит Тормоз.
Запишем высказывания (высказывание Петра «Тормоз готовился очень тщательно» не содержит информации о месте и не может быть учтено):
Учитывая истинность предположений двух друзей и ложность третьего, запишем истинное высказывание, основанное на том, что неправ либо первый, либо второй, либо третий:
Затем упростим его за счет двойного отрицания, правила Моргана и убрав ненужные для первого члена скобки:
[¬Л /\ С /\ Л /\ ¬Т /\ С] \/ [(Л \/ ¬С) /\ (¬Л \/ Т) /\ ¬С] \/ [(Л \/ ¬С) /\ (Л /\ ¬Т) /\ ¬С] = 1
Выражение по-прежнему немаленькое. Далее, по закону поглощения можно сократить показанное красным
[ ¬Л /\ С /\ Л /\ ¬Т /\ С] \/ [ (Л \/ ¬С) /\ (¬Л \/ Т) /\ ¬С ] \/ [ (Л \/ ¬С) /\ (Л /\ ¬Т) /\ ¬С ] = 1
[(¬Л \/ Т) /\ ¬С] \/ [(Л /\ ¬Т) /\ ¬С] = 1
В оставшейся части сократим противоположные слагаемые (по закону исключения третьего)
Конечно, можно сразу сказать, что в произведении все три множителя должны быть равны единице, то есть: Л = 1, Т = 0, С = 0. Ответ: победителем скачек стала Ласточка.
Но можно сделать то же, построив таблицу истинности: