Что такое высота параллелограмма
Параллелограмм: свойства и признаки
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны и равны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
Биссектриса угла параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
Как найти площадь параллелограмма:
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
Теорема доказана. Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
Шаг 3. Из равенства треугольников также следует:
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:
Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.
Каковы основание и высота параллелограмма?
Кроме того, какова формула основания?
Итак, какова формула определения высоты?
Включите свои ценности в уравнение A = 1 / 2bh и сделай математику. Сначала умножьте основание (b) на 1/2, затем разделите площадь (A) на произведение. Полученное значение будет высотой вашего треугольника!
Также знать, как измерить параллелограмм? Где b = основание параллелограмма (AB) h = высота параллелограмма. a = сторона параллелограмма (AD)
| Все формулы для вычисления площади параллелограмма | |
|---|---|
| Использование базы и высоты | A = b × h |
| Использование тригонометрии | А = ab sin (х) |
Какая высота у фигуры?
Какова высота прямоугольного треугольника?
Какая высота у треугольника?
Какая формула диагонали параллелограмма?
Часто задаваемые вопросы о диагонали формулы параллелограмма
Диагонали параллелограмма?
Параллелограмм?
Что такое ДхШхВ?
Какая ширина и высота?
Какова высота равнобедренного треугольника?
Отвечать. Мы можем найти высоту, разделив равнобедренный треугольник на два прямоугольных, а затем применив теорему Пифагора к одному из них. h = 13.20 (до 2 дн.
Что такое H в прямоугольном треугольнике?
В любом прямоугольном треугольнике диаметр вписанной окружности меньше половины гипотенузы и, что более важно, меньше или равен временам гипотенузы. В прямоугольном треугольнике с катетами a, b и гипотенузой c равенство выполняется только в равнобедренном случае. Если высота от гипотенузы равна обозначается hc, тогда.
Как найти высоту равнобедренного треугольника?
Отвечать. Мы можем найти высоту, разделив равнобедренный треугольник на два прямоугольных, а затем применив теорему Пифагора к одному из них. h = 13.20 (до 2 дн.
Как определить высоту треугольника с учетом двух сторон?
Какая диагональ у параллелограмма длиннее?
По какой формуле найти диагональ?
Какова длина большей диагонали в параллелограмме быстрого?
Ответ: Длина самой длинной диагонали параллелограмма равна 24.86.
Что делает параллелограмм?
У параллелограмма четыре прямых угла?
Прямоугольник представляет собой параллелограмм с четырьмя прямыми углами, поэтому все прямоугольники также являются параллелограммами и четырехугольниками.
Какой пример для параллелограмма?
В геометрии четырехугольник называется параллелограммом. У параллелограмма противоположные стороны параллельны и равны по длине. Несколько примеров параллелограмма: ромб, прямоугольник и квадрат.
Какая форма у параллелограмма?
Параллелограмм: Четырехугольник с 2 парами параллельных сторон.
Чем не параллелограмм?
Параллелограммы
 Свойства и признаки параллелограмма Свойства и признаки параллелограмма |
 Свойства и признаки прямоугольника Свойства и признаки прямоугольника |
 Свойства и признаки ромба Свойства и признаки ромба |
 Свойства и признаки квадрата Свойства и признаки квадрата |
Свойства и признаки параллелограмма
Определение: Параллелограммом называют четырёхугольник, у которого противолежащие стороны параллельны
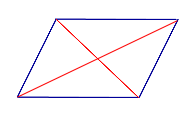
Определение: Диагональю параллелограмма называют отрезок, соединяющий противоположные вершины
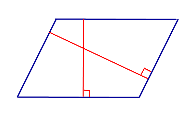
Определение: Высотой параллелограмма называют перпендикуляр, опущенный из любой точки на стороне параллелограмма на противоположную сторону параллелограмма или ее продолжение
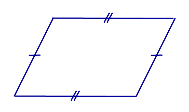
Свойство: Если четырёхугольник является параллелограммом, то его противолежащие стороны равны.
Признак: Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом.
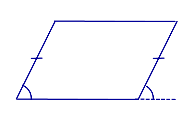
Признак: Если у четырёхугольника две противолежащие стороны равны и параллельны, то он является параллелограммом.
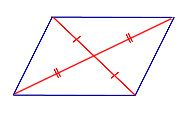
Свойство: Если четырёхугольник является параллелограммом, то его диагонали точкой пересечения делятся пополам.
Признак: Если у четырёхугольника диагонали точкой пересечения делятся пополам, то он является параллелограммом.
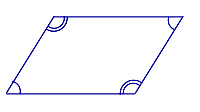

Свойство: Если четырёхугольник является параллелограммом, то его противолежащие углы равны.
Признак: Если у четырёхугольника противолежащие углы равны, то четырёхугольник является параллелограммом.
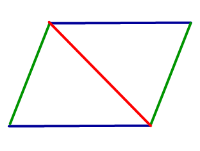
Свойство: Если четырёхугольник является параллелограммом, то каждая диагональ делит его на два равных треугольника.
Признак: Если каждая диагональ четырёхугольника делит его на два равных треугольника, то четырёхугольник является параллелограммом.
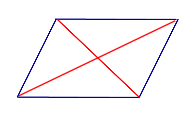
Свойство: Если четырёхугольник является параллелограммом, то диагонали делит его на четыре треугольника равной площади (равновеликих треугольника)
Признак: Если диагонали четырёхугольника делят его на четыре треугольника равной площади (равновеликих треугольника), то четырёхугольник является параллелограммом.
Свойства и признаки прямоугольника
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Прямоугольник |  | Прямоугольником называют параллелограмм, у которого все углы прямые |
| Свойство | Равенство диагоналей | 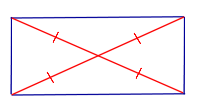 | Если параллелограмм является прямоугольником, то его диагонали равны |
| Признак | Если у параллелограмма диагонали равны, то он является прямоугольником |
| Определение: прямоугольник | |
 | Прямоугольником называют параллелограмм, у которого все углы прямые |
| Свойство: равенство диагоналей | |
 | Если параллелограмм является прямоугольником, то его диагонали равны |
| Признак: равенство диагоналей | |
 | Если у параллелограмма диагонали равны, то он является прямоугольником |
Определение: Прямоугольником называют параллелограмм, у которого все углы прямые.

Свойство: Если параллелограмм является прямоугольником, то его диагонали равны.
Признак: Если у параллелограмма диагонали равны, то он является прямоугольником.
Свойства и признаки ромба
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Ромб |  | Ромбом называют параллелограмм, у которого все стороны равны |
| Свойство | Биссектрисы углов диагонали | 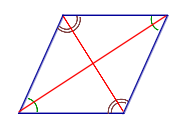 | Если параллелограмм является ромбом, то его диагонали является биссектрисами углов |
| Признак | Если у параллелограмма диагонали являются биссектрисами углов, то параллелограмм является ромбом | ||
| Свойство | Перпендикулярность диагоналей | 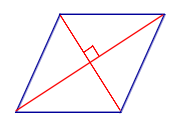 | Если параллелограмм является ромбом, то его диагонали перпендикулярны |
| Признак | Если у параллелограмма диагонали перпендикулярны, то он является ромбом |
| Определение: ромб | |
 | Ромбом называют параллелограмм, у которого все стороны равны |
| Свойство: биссектрисы углов и диагонали | |
 | Если параллелограмм является ромбом, то его диагонали являются биссектрисами углов |
| Признак: биссектрисы углов и диагонали | |
 | Если у параллелограмма диагонали являются биссектрисами углов, то параллелограмм является ромбом |
| Свойство: перпендикулярность диагоналей | |
 | Если параллелограмм является ромбом, то его диагонали перпендикулярны |
| Признак: перпендикулярность диагоналей | |
 | Если у параллелограмма диагонали перпендикулярны, то он является ромбом |
Определение: Ромбом называют параллелограмм, у которого все стороны равны

Признак: Если у параллелограмма диагонали являются биссектрисами углов, то параллелограмм является ромбом

Свойство: Если параллелограмм является ромбом, то его диагонали перпендикулярны
Признак: Если у параллелограмма диагонали перпендикулярны, то он является ромбом
Свойства и признаки квадрата
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Квадрат | 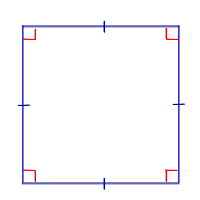 | Квадратом называют параллелограмм, у которого все стороны равны и все углы равны |
| Свойство | Перпендикулярность и равенство диагоналей | 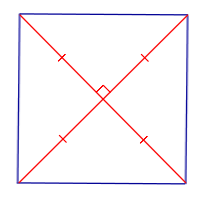 | Если параллелограмм является квадратом, то его диагонали перпендикулярны и равны |
| Признак | Если у параллелограмма диагонали перпендикулярны и равны, то он является квадратом | ||
| Свойство | Перпендикулярность диагоналей | Если прямоугольник является квадратом, то его диагонали перпендикулярны | |
| Признак | Если у прямоугольника диагонали перпендикулярны, то он является квадратом | ||
| Свойство | Равенство диагоналей | 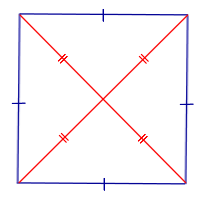 | Если ромб является квадратом, то его диагонали равны |
| Признак | Если у ромба диагонали равны, то он является квадратом |
| Определение: квадрат | |
 | Квадратом называют параллелограмм, у которого все стороны равны и все углы равны |
| Свойство: перпендикулярность и равенство диагоналей | |
 | Если параллелограмм является квадратом, то его диагонали перпендикулярны и равны |
| Признак: перпендикулярность и равенство диагоналей | |
 | Если у параллелограмма диагонали перпендикулярны и равны, то он является квадратом |
| Свойство: перпендикулярность диагоналей | |
 | Если прямоугольник является квадратом, то его диагонали перпендикулярны |
| Признак: перпендикулярность диагоналей | |
 | Если у прямоугольника диагонали перпендикулярны, то он является квадратом |
| Свойство: равенство диагоналей | |
 | Если ромб является квадратом, то его диагонали равны |
| Признак: равенство диагоналей | |
 | Если у ромба диагонали равны, то он является квадратом |
Определение: Квадратом называют параллелограмм, у которого все стороны равны и все углы равны

Свойство: Если параллелограмм является квадратом, то его диагонали перпендикулярны и равны
Признак: Если у параллелограмма диагонали перпендикулярны и равны, то он является квадратом

Свойство: Если прямоугольник является квадратом, то его диагонали перпендикулярны
Признак: Если у прямоугольника диагонали перпендикулярны, то он является квадратом

Свойство: Если ромб является квадратом, то его диагонали равны
Признак: Если у ромба диагонали равны, то он является квадратом
Как найти высоту параллелограмма
В задачах по геометрии, точнее по планиметрии и тригонометрии, иногда требуется найти высоту параллелограмма, исходя из заданных значений сторон, углов, диагоналей и т.п.
Чтобы найти высоту параллелограмма, зная его площадь и длину основания, необходимо воспользоваться правилом определения площади параллелограмма. Площадь параллелограмма, как известно, равняется произведению высоты на длину основания:
Отсюда получаем, что высота параллелограмма будет равняться площади, разделенной на длину основания:
найти: высоту параллелограмма.
Так как высота параллелограмма, часть основания и прилежащая к основанию сторона образуют прямоугольный треугольник, то для нахождения высоты параллелограмма можно использовать некоторые соотношения сторон и углов прямоугольных треугольников.
Если известны прилежащая к высоте h (DE) сторона параллелограмма d (AD) и противоположный высоте угол A (BAD), то расчета высоты параллелограмма нужно умножить длину прилежащей стороны на синус противоположного угла:
например, если d=10 см, а угол А=30 градусов, то
Если в условиях задачи заданы длина прилежащей к высоте h (DE) стороне параллелограмма d (AD) и длина отсекаемой высотой части основания (АЕ), то высоту параллелограмма можно найти воспользовавшись теоремой Пифагора:
|AE|^2+|ED|^2=|AD|^2, откуда определяем:
т.е. высота параллелограмма равняется корню квадратному из разности квадратов длины прилежащей стороны и отсекаемой высотой части основания.
Например, если длина прилегающей стороны равняется 5 см., а длина отсекаемой части основания равна 3 см, то длина высоты будет:
Если известны длина прилежащей к высоте диагональ (DВ) параллелограмма и длина отсекаемой высотой части основания (ВЕ), то высоту параллелограмма можно также найти воспользовавшись теоремой Пифагора:
|ВE|^2+|ED|^2=|ВD|^2, откуда определяем:
т.е. высота параллелограмма равняется корню квадратному из разности квадратов длины прилежащей диагонали и отсекаемой высотой (и диагональю) части основания.
Например, если длина прилегающей стороны равняется 5 см., а длина отсекаемой части основания равна 4 см, то длина высоты будет:
Опорный конспект на тему «Параллелограмм и его виды» (8 класс)
B C Параллелограмм – это четырехугольник,
у которого противолежащие стороны попарно
параллельны.
B C Параллелограмм – это четырехугольник,
у которого противолежащие стороны попарно
параллельны.
У параллелограмма противолежащие стороны равны, противолежащие углы равны.
Сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.
A + B = 180° (т. к. A и B – внутренние односторонние при BC ‖ AD и секущей AB )
Диагонали параллелограмма точкой пересечения делятся пополам.
У параллелограмма противолежащие стороны равны, противолежащие углы равны.
Сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.
A + B = 180° (т. к. A и B – внутренние односторонние при BC ‖ AD и секущей AB )
Диагонали параллелограмма точкой пересечения делятся пополам.
Высота параллелограмма – перпендикуляр, опущенный из любой точки прямой, содержащей сторону параллелограмма, на прямую, содержащую противолежащую сторону.
BK и ВМ – высоты, проведенные
Свойства биссектрис параллелограмма
Биссектриса угла параллелограмма
отсекает от него равнобедренный
Биссектрисы соседних углов
О параллелограмма пересекаются
Свойства высот параллелограмма
B C Угол между высотами, проведенными
из вершины тупого угла параллелограмма,
равен острому углу параллелограмма.
Угол между высотами, проведенными
A K D из вершины острого угла параллелограмма,
равен тупому углу параллелограмма.
Высота параллелограмма – перпендикуляр, опущенный из любой точки прямой, содержащей сторону параллелограмма, на прямую, содержащую противолежащую сторону.
BK и ВМ – высоты, проведенные
Свойства биссектрис параллелограмма
Биссектриса угла параллелограмма
отсекает от него равнобедренный
Биссектрисы соседних углов
О параллелограмма пересекаются
Свойства высот параллелограмма
B C Угол между высотами, проведенными
из вершины тупого угла параллелограмма,
равен острому углу параллелограмма.
Угол между высотами, проведенными
A K D из вершины острого угла параллелограмма,
равен тупому углу параллелограмма.
Если в четырехугольнике
противолежащие стороны попарно равны,
противолежащие стороны равны и параллельны,
диагонали пересекаются и точкой пересечения делятся пополам,
то этот четырехугольник – параллелограмм.
Если в четырехугольнике
противолежащие стороны попарно равны,
противолежащие стороны равны и параллельны,
диагонали пересекаются и точкой пересечения делятся пополам,
то этот четырехугольник – параллелограмм.
Прямоугольник Квадрат Ромб
Прямоугольник Квадрат Ромб
Все свойства параллелограмма.
Диагонали прямоугольника равны.
Если один из углов параллело-грамма прямой, то этот парал-лелограмм – прямоугольник.
Если в параллелограмме диаго-нали равны, то этот параллело-грамм – прямоугольник.
Все свойства параллелограмма.
Диагонали ромба перпендику-лярны и являются биссектри-сами его углов.
D Значит, ВО – и бис-
сектриса,и высота.
Если в четырехугольнике все стороны равны, то этот четырехугольник – ромб.
Если в параллелограмме две соседние стороны равны, то этот параллелограмм – ромб.
Если диагонали параллелограмма перпендикулярны, то этот параллелограмм – ромб.
Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм – ромб.
Все свойства параллелограмма.
Все свойства прямоугольника.
Все свойства ромба.
Если диагонали прямоугольника перпендикулярны, то этот прямоугольник – квадрат.
Если диагональ прямоугольника является биссектрисой его угла, то этот прямоугольник – квадрат.
Если диагонали ромба равны, то этот ромб – квадрат.
Все свойства параллелограмма.
Диагонали прямоугольника равны.
Если один из углов параллело-грамма прямой, то этот парал-лелограмм – прямоугольник.
Если в параллелограмме диаго-нали равны, то этот параллело-грамм – прямоугольник.
Все свойства параллелограмма.
Диагонали ромба перпендику-лярны и являются биссектри-сами его углов.
D Значит, ВО – и бис-
сектриса,и высота.
Если в четырехугольнике все стороны равны, то этот четырехугольник – ромб.
Если в параллелограмме две соседние стороны равны, то этот параллелограмм – ромб.
Если диагонали параллелограмма перпендикулярны, то этот параллелограмм – ромб.
Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм – ромб.
Все свойства параллелограмма.
Все свойства прямоугольника.
Все свойства ромба.
Если диагонали прямоугольника перпендикулярны, то этот прямоугольник – квадрат.
Если диагональ прямоугольника является биссектрисой его угла, то этот прямоугольник – квадрат.
Если диагонали ромба равны, то этот ромб – квадрат.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Для более успешного усвоения большого теоретического материала и экономии времени на уроке можно использовать раздаточный материал в виде опорного конспекта.
Предлагаемый конспект содержит определение параллелограмма, его свойства, признаки, а также свойства и признаки прямоугольника, ромба и квадрата. При распечатке рассчитан на двух учеников.
Номер материала: ДБ-388025
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Онлайн-конференция о профориентации и перспективах рынка труда
Время чтения: 3 минуты
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Время чтения: 2 минуты
Пик использования смартфонов приходится на 16 лет
Время чтения: 1 минута
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.







