Что такое высота в геометрии кратко
Высота (геометрия)
Высота трапеции, призмы, цилиндра, шарового слоя, усеченных параллельно основанию — расстояние между верхним и нижним основаниями.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
В геометрии конциклическими (или гомоциклическими) точками называют точки, находящиеся на одной окружности. Три точки на плоскости, не лежащие на одной прямой, всегда лежат на одной окружности, поэтому иногда термин «конциклические» прилагают только к наборам из 4 или более точек.
В математике и физике барице́нтр, или геометри́ческий центр, двумерной области — это среднее арифметическое положений всех точек фигуры. Определение распространяется на любой объект в n-мерном пространстве — барицентр является средним положением всех точек фигуры по всем координатным направлениям. Неформально — это точка равновесия фигуры, вырезанной из картона в предположении, что картон имеет постоянную плотность и гравитационное поле постоянно по величине и направлению.
Пра́вильный двадцатичетырёхъяче́йник, или просто двадцатичетырёхъяче́йник, или икоситетрахор (от др.-греч. εἴκοσι — «двадцать», τέτταρες — «четыре» и χώρος — «место, пространство»), — один из правильных многоячейников в четырёхмерном пространстве.
В геометрии трилинейными полярами являются некоторые специальные виды прямой линии, связанные с плоскостью треугольника и лежащие в плоскости треугольника. Трилинейная поляра точки Y (полюса) относительно невырожденного треугольника это — прямая линия, определяемая следующим построением. Если продолжить стороны чевианного треугольника некоторой точки и взять их точки пересечения с соответствующими сторонами, то полученные точки пересечения будут лежать на одной прямой, называемой трилинейной исходной.
Говорят, что два и более объектов концентричны или коаксиальны, если они имеют один и тот же центр или ось. Окружности, правильные многоугольники, правильные многогранники и сферы могут быть концентричны друг другу (имея одну и ту же центральную точку), как могут быть концентричными и цилиндры (имея общую коаксиальную ось).
Высота (геометрия)
Высота в элементарной геометрии — отрезок перпендикуляра, опущенного из вершины геометрической фигуры (например, треугольника, пирамиды, конуса) на её основание или на продолжение основания. Под высотой также подразумевается длина этого отрезка.
Высота трапеции, призмы, цилиндра, шарового слоя, усеченных параллельно основанию — расстояние между верхним и нижним основаниями.
Высота треугольника
Высота треугольника — отрезок, опущенный из вершины треугольника перпендикулярно противоположной стороне.
Все высоты треугольника пересекаются в одной точке, называемой ортоцентром этого треугольника. — Эту теорему легко доказать, используя векторное тождество, справедливое для любых точек A, B, C, E, не обязательно даже лежащих в одной плоскости:
(Для доказательства следует взять в качестве точки E пересечение двух высот треугольника.)
Площадь треугольника равна половине произведения высоты треугольника на соответствующее основание. Кроме формулы, удобной для расчёта площади, из этого также следует, что длины высот треугольника обратно пропорциональны длинам соответствующих сторон.
Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:
1. Минимальная ортогональная проекция треугольника на прямую, лежащую в плоскости треугольника, имеет длину, равную наименьшей из его высот.
2. Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.
3. При непрерывном движении двух точек по периметру треугольника друг навстречу другу, если они встречаются хотя бы дважды, тогда максимальное расстояние между точками во время их движения не может быть меньше длины наименьшей из высот треугольника.
Полезное
Смотреть что такое «Высота (геометрия)» в других словарях:
Высота треугольника — У этого термина существуют и другие значения, см. Высота (значения). Высота в треугольниках различного типа Высота треугольника перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону. В зав … Википедия
ВЫСОТА — в диофантовой геометрии некоторая численная функция на множестве решений диофантова уравнения. В простейшем случае целочисленного решения диофантова уравнения высота есть функция решения, равная В таком виде она встречается уже в методе спуска… … Математическая энциклопедия
МНОГОМЕРНАЯ ГЕОМЕТРИЯ — геометрия пространств размерности, большей трех; термин применяется к тем пространствам, геометрия к рых была первоначально развита для случая трех измерений и только потом обобщена на число измерений n>3, прежде всего евклидово пространство,… … Математическая энциклопедия
Пирамида (геометрия) — У этого термина существуют и другие значения, см. Пирамидацу (значения). Достоверность этого раздела статьи поставлена под сомнение. Необходимо проверить точность фактов, изложенных в этом разделе. На странице обcуждения могут быть пояснения … Википедия
Объём (геометрия) — У этого термина существуют и другие значения, см. Объём (значения). Объём это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого… … Википедия
N-мерная евклидова геометрия — N мерная евклидова геометрия обобщение евклидовой геометрии на пространство большего числа измерений. Хотя физическое пространство является трёхмерным[1], и человеческие органы чувств рассчитаны на восприятие трёх измерений[2], N мерная… … Википедия
ДИОФАНТОВА ГЕОМЕТРИЯ — диофантов анализ, область математики, посвященная изучению целочисленных и рациональных решений систем алгебраич. уравнений, или, иначе, изучению диофантовых уравнений, методами алгебраич. геометрии. Появление во 2 й пол. 19 в. теории алгебраич.… … Математическая энциклопедия
Объем (геометрия) — Объём это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого определения в отношении трёхмерных тел трёхмерного евклидова пространства.… … Википедия
Призма (геометрия) — У этого термина существуют и другие значения, см. Призма … Википедия
Сектор (геометрия) — У этого термина существуют и другие значения, см. Сектор. Сектор круга закрашен зелёным Сектор в геометрии часть круга, ограниченная дугой и двумя ра … Википедия
Треугольник. Высота треугольника.
Высота треугольника – перпендикуляр, прочерченный из выбранной вершины треугольника на противолежащею его сторону. Для обозначения высоты треугольника используют букву h, к ней добавляется название той стороны, к которой она прочерчена: ha, hb, hc,
Сторону треугольника, к которой прочерчена высота, называют основанием треугольника.
Высота треугольника может быть прочерчена к любой из трех сторон треугольника. Случается высота треугольника пересекает не само основание треугольника, а его продолжение. Так, высоты AD и ЕМ пересекают продолжения оснований ВС и FK.
Характерные особенности высоты.
В прямоугольном треугольнике высота, прочерченная из вершины прямого угла, разделит его на два треугольника, подобные первоначальному.
В остроугольном треугольнике две его высоты отделяют от него подобные треугольники.
Если треугольник остроугольный, то все основания высот принадлежат его сторонам, а у тупоугольного треугольника две высоты принадлежат продолжению сторон.
Три высоты в остроугольном треугольнике перекрещиваются в одной точке и эту точку обозначают как ортоцентр треугольника.
Определение и свойства высоты треугольника
В данной публикации мы рассмотрим определение высоты треугольника, продемонстрируем, как она выглядит в зависимости от вида треугольника, а также перечислим ее основные свойства.
Определение высоты треугольника
Высота треугольника – это перпендикуляр, который опущен из вершины фигуры на противоположную сторону.
Основание высоты – точка на противоположной стороне треугольника, которую пересекает высота (или точка пересечения их продолжений).
Обычно высота обозначается буквой h (иногда как ha – это означает, что она проведена к стороне a).
Высота в разных видах треугольников
В зависимости от вида фигуры высота может:
Свойства высоты треугольника
Свойство 1
Все три высоты в треугольнике (или их продолжения) пересекаются в одной точке, которая называется ортоцентром (точка O на чертежах ниже).
Свойство 2
При пересечении двух высот в треугольнике, образуются следующие подобные треугольники:
Свойство 3
Точка пересечения высот в остроугольном треугольнике является центром окружности, вписанной в его ортотреугольник.
Ортотреугольник – треугольник, вершинами которого являются основания высот △ABC. В нашем случае – это △DEF.
Свойство 4
Точки, которые симметричны ортоцентру треугольника относительно его сторон, лежат на окружности, описанной вокруг этого треугольника.
Примечание: формулы для нахождения высоты треугольника подробно рассмотрены в нашей публикации – “Как найти высоту в треугольнике abc”.
Высота треугольника

Всего получено оценок: 78.
Всего получено оценок: 78.
Почти никогда не получится определить все параметры треугольника без дополнительных построений. Эти построения являются своеобразными графическими характеристиками треугольника, которые помогают определить величину сторон и углов.
Определение
Одной из таких характеристик является высота треугольника. Высота – это перпендикуляр, проведенный из вершины треугольника к его противоположной стороне. Вершиной называют одну из трех точек, которые вместе с тремя отрезками составляют треугольник.
Определение высоты треугольника может звучать и так: высота – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Это определение звучит сложнее, но оно точнее отражает ситуацию. Дело в том, что в тупоугольном треугольнике не получится провести высоту внутри треугольника. Как видно на рисунке 1, высота в этом случае получается внешней. Кроме того, нестандартной ситуацией является построение высоты в прямоугольном треугольнике. В этом случае, две из трех высот треугольника будут проходить через катеты, а третья от вершины к гипотенузе.
Как правило, высоту треугольника обозначают буквой h. Также обозначается высота и в других фигурах.
Как найти высоту треугольника?
Существует три стандартных способа нахождения высоты треугольника:
Через теорему Пифагора
Этот способ применяется для равносторонних и равнобедренных треугольников. Разберем решение для равнобедренного треугольника, а потом скажем, почему это же решение справедливо для равностороннего.
Дано: равнобедренный треугольник АВС с основанием АС. АВ=5, АС=8. Найти высоту треугольника.
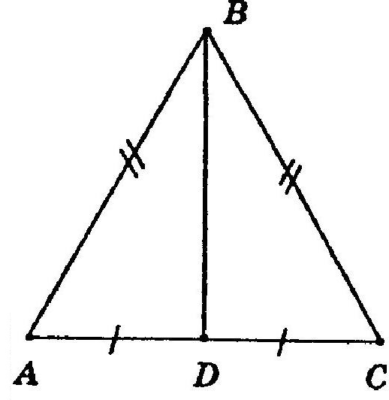
Для равнобедренного треугольника важно знать, какая именно сторона является основанием. Это определяет боковые стороны, которое должны быть равны, а так же высоту, на которую действую некоторые свойства.
Свойства высоты равнобедренного треугольника, проведенной к основанию:
Высоту обозначим, как ВD. DС найдем как половину от основания, так как высота точкой D делит основание пополам. DС=4
Высота – это перпендикуляр, значит ВDС – прямоугольный треугольник, а высота ВD является катетом этого треугольника.
Любой равносторонний треугольник является равнобедренным, только основание у него равно боковым сторонам. То есть, можно использовать тот же порядок действий.
Через площадь треугольника
Этим способом можно пользоваться для любого треугольника. Чтобы им воспользоваться, нужно знать значение площади треугольника и стороны, к которой проведена высота.
Высоты в треугольнике не равны, поэтому для соответствующей стороны получится вычислить соответствующую высоту.
Через тригонометрическую функцию
Третий способ подойдет, если известна сторона и угол при основании. Для этого придется воспользоваться тригонометрической функцией.
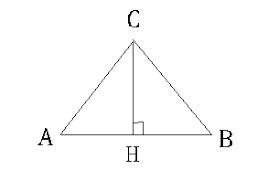
Угол известен, как и сторона. Выразим высоту треугольника:
Значение косинуса в общем случае берется из таблиц Брадиса, но значения тригонометрических функций для 30,45 и 60 градусов – табличные числа.
Что мы узнали?
Мы узнали, что такое высота треугольника, какие бывают высоты и как они обозначаются. Разобрались в типовых задачах и записали три формулы для высоты треугольника.





