Что такое взаимная ориентация векторов
Большая Энциклопедия Нефти и Газа
Комбинация методик измерения, предложенных Чекалла и Лабхартом, дает удобный способ определения не только диполь-ных моментов, но и ( в более сложных случаях) взаимной ориентации векторов дипольных моментов и момента перехода. [19]
В итоге величина угла взаимной ориентации векторов МДС обмоток ротора и статора двигателя при движении машины остается такой же, какой ее установили при покое. Механическая характеристика электропривода в этом режиме получается абсолютно мягкой. Частота напряжения на статоре двигателя автоматически устанавливается равной его скорости вращения. [22]
Указанные типы дислокаций являются предельными, поскольку предельными ( 0 и л / 2) будут углы между векторами Бюргерса и осями дислокаций. Помимо них встречаются промежуточные случаи взаимной ориентации вектора Бюргерса и оси дислокации. Угол а не обязательно постоянен вдоль дислокации, поскольку дислокации могут быть и криволинейными. Однако величина относительного смещения двух частей кристалла неизменна, и поэтому вектор Бюргерса по всей длине любой дислокации остается постоянным. Дислокационные линии могут заканчиваться на поверхности кристалла, границах зерен, других дислокациях, могут образовывать замкнутые петли. Дислокационные линии в виде замкнутой петли называют дислокационной петлей. [23]
Значение элементарной работы силы зависит от выбора системы отсчета. Кроме того, в зависимости от взаимной ориентации векторов F и Аг элементарная работа может быть величиной положительной, отрицательной или равной нулю. [24]
Значение элементарной работы силы зависит от выбора системы отсчета. Кроме того, в зависимости от взаимной ориентации векторов F и Дг элементарная работа может быть величиной положительной, отрицательной или равной нулю. [25]
В атоме обычно имеется много электронов, и суммарный момент его складывается из моментов отдельных электронов. В приближении рессель-саундеровской связи, когда релятивистское взаимодействие электронов, зависящее от взаимной ориентации векторов орбитального и спинового моментов, мало по сравнению с их электростатическим взаимодействием, полный орбитальный L и спиновый S моменты атома складываются соответственно из орбитальных и спиновых моментов отдельных электронов. [26]
Фазовая глубина дорожек может быть определена как разность фаз отраженных от верхней и нижней частей структуры полей, измеренная в плоскости непосредственно над структурой. Эта фазовая глубина представляет собой эффективную глубину дорожки для падающего света и, очевидно, зависит от взаимной ориентации вектора поляризации и направления дорожек. Фазовая глубина представляет особый интерес для описания процесса воспроизведения информации с оптических дисков. [28]
Ядерные спины и магнитные моменты иногда могут быть определены на основании изучения сверхтонкой структуры атомных спектров. Сверхтонкая структура обусловлена тем обстоятельством, что вследствие взаимодействия между магнитным моментом ядра и магнитными моментами электронов энергия атома несколько различна для различных квантованных взаимных ориентации векторов спина ядра и вращательных моментов электронов. [29]
Падение плоской волны с параллельной поляризацией
Будем полагать, что на идеально проводящую поверхность под некоторым углом 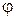
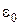
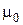
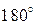
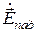
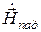
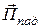
Известно, что граничные условия на поверхности идеального проводника заключаются в равенстве нулю тангенциальной составляющей электрического вектора на границе раздела. Выполнение данного условия возможно лишь при наличии отраженной волны.
Рисунок 9 − Падение плоской электромагнитной волны с параллельной поляризацией на идеально проводящую плоскость
На рисунке 9 построена система поверхностей равных фаз для отраженной волны, векторы поля которой обладают следующими свойствами:
1. Амплитуды 

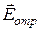
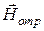
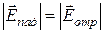
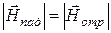
2. Направление 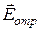

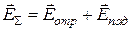
3. Взаимная ориентация векторов 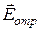
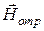
Проведем теперь векторное сложение полей падающей и отраженной волны в узлах образующейся сетки волновых поверхностей. Результат его представлен на рисунке, причем могут быть сделаны следующие выводы:
1. Силовые линии суммарного магнитного поля имеют вид бесконечных нитей, направленных параллельно оси 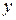
2. Векторы 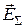

Рисунок 10 − Результирующая картина силовых линий поля при падении плоской волны с параллельной поляризацией
Полученная картина векторной интерференции позволяет построить эскиз силовых линий результирующего волнового процесса. Для этого, например, силовые линии поля 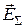
Следует принять во внимание, что рассматривались лишь те волновые фронты, в пределах которых мгновенные значения векторов поля максимальны. Если произвести более детальное построение, включив в рассмотрение волновые фронты с промежуточными значениями фазы, то получим окончательную картину силовых линий, изображенную на рисунке. Здесь графически показано постепенное изменение напряженностей поля в пространстве.
Дата добавления: 2015-10-19 ; просмотров: 1205 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
3.5.5 Свойства электромагнитных волн. Взаимная ориентация векторов в электромагнитной волне в вакууме
Видеоурок: Опыты Герца. Свойства электромагнитных волн
Лекция: Свойства электромагнитных волн. Взаимная ориентация векторов в электромагнитной волне в вакууме
Опыты Максвелла доказали, что электрический ток в вакууме распространяется со скоростью, с которой движется свет, то есть 3*10 8 м/с.

Чем быстрее будет происходить перемещение заряда, тем выразительнее будут электромагнитные волны. То есть, чем больше частота, тем большая интенсивность электромагнитных волн.
На частоту колебательного контура влияет индуктивность и ёмкость составляющих элементов цепи. Определить её можно по следующей формуле:
Электромагнитные волны являются поперечными. Это значит, что колебания магнитного и электрического поля происходят в плоскостях, которые являются параллельными к распространению волны.
На графике можно рассмотреть электрическую и магнитную составляющую электромагнитной волны.
Стоит отметить, что силовые характеристики магнитного и электрического поля находятся под углом 90 градусов друг к другу.
На графике показана длина волны, которая обозначается λ. Для её определения необходимо воспользоваться формулой:

Электромагнитным волнам присущи все правила, справедливые для механических волн:
1. Стоит отметить, что электромагнитная волна способна отразиться от плотного металла.
2. Через диэлектрик электромагнитная волна проходит достаточно проблематично, поскольку она им поглощается.
3. Если электромагнитная волна переходит из одной среды в другую, которая отличается плотностью, то она способна преломиться.
Угол между векторами. Ориентация пары векторов на плоскости или тройки векторов в пространстве.
Если речь идет о векторах на плоскости, то можем ввести понятие ориентированного угла между векторами. Если кратчайший поворот


Проекция вектора на ось.
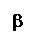

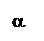
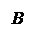






Зная скалярную проекцию вектора мы можем найти его векторную проекцию:
Теорема 2. Свойства проекции вектора на ось.

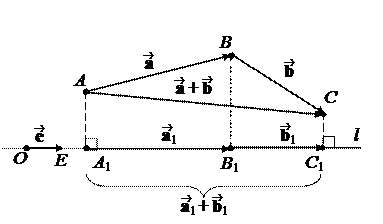
1 случай: j £ p/2. Тогда из DOBB1 получим, что
2 случай: j > p/2. Тогда из DOBB1 получим, что
2. Для скалярных проекций:
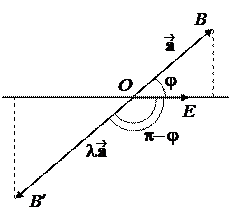

Ð(, l ) = p – j и cosÐ(,l ) = – cos j,
3случай: l = 0. Тогда равенство очевидно.
Для векторных проекций с помощью равенства (*) получаем:
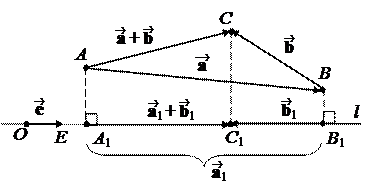

Что такое взаимная ориентация векторов
Для любых двух базисов на прямой, на плоскости и в пространстве определяются понятия одинаковой или различной ориентированности этих базисов. На прямой два базиса одинаковой ориентации — это просто два сонаправленных вектора, а два базиса различной ориентации — это два противоположно направленных вектора.
На плоскости два базиса а, b и 
Тройка базисных векторов в пространстве называется правой (левой), если эти векторы, отложенные от одной точки, располагаются так, как расположены соответственно большой, указательный и согнутый средний пальцы правой (левой) руки (рис. 22.24).
В том случае, когда имеются две правые или две левые тройки векторов, говорят, что эти тройки (базисы) имеют одинаковую ориентацию или что они ориентированы одинаково.
Если же из двух данных базисов один является правой тройкой, а другой — левой тройкой векторов, то говорят, что эти базисы имеют различную ориентацию или что они ориентированы противоположно.
В дальнейшем векторы i, j, k мы всегда выбираем так, чтобы они образовывали правую тройку векторов.