Что такое взаимно однозначное отображение
Биекция
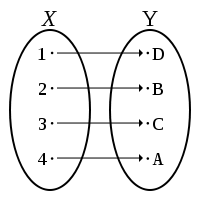
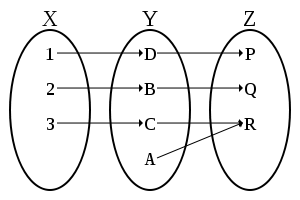
Биекция — это отображение, которое является одновременно и сюръективным, и инъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом, определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют ещё взаимно-однозначным отображением (соответствием), одно-однозначным отображением.
Если между двумя множествами можно установить взаимно-однозначное соответствие (биекция), то такие множества называются равномощными. С точки зрения теории множеств, равномощные множества неразличимы.
Взаимно-однозначное отображение конечного множества в себя называется перестановкой (элементов этого множества).
Содержание
Определение
Функция 

Примеры
Свойства
Применения
В информатике
Организация связи «один к одному» между таблицами реляционной БД на основе первичных ключей.
Примечания
См. также
Литература
Полезное
Смотреть что такое «Биекция» в других словарях:
биекция — взаимно однозначное соответствие — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия Синонимы взаимно однозначное соответствие EN one to one onto function … Справочник технического переводчика
биекция (в криптографии) — биекция Взаимно однозначное отображение. [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] Тематики защита информации EN bijection … Справочник технического переводчика
Изоморфизм — У этого термина существуют и другие значения, см. Изоморфизм (значения). Изоморфизм (от др. греч. ἴσος «равный, одинаковый, подобный» и μορφή «форма») это очень общее понятие, которое употребляется в различных разделах математики. В общих… … Википедия
Изоморфизм (математика) — Изоморфизм это очень общее понятие, которое употребляется в различных разделах математики. В общих чертах его можно описать так: Пусть даны два множества с определённой структурой (группы, кольца, линейные пространства и т. п.). Биекция между… … Википедия
Изоморфизм (матем.) — Изоморфизм это очень общее понятие, которое употребляется в различных разделах математики. В общих чертах его можно описать так: Пусть даны два множества с определённой структурой (группы, кольца, линейные пространства и т. п.). Биекция между… … Википедия
Граф (математика) — У этого термина существуют и другие значения, см. Граф (значения). Неориентированный граф с шестью вершинами и семью рёбрами В математической теории графов и информатике граф это совокупность непустого множества вершин и множества пар… … Википедия
Парадокс Сколема — представляет собой рассуждение, связанное с использованием теоремы Лёвенгейма Сколема для аксиоматической теории множеств. В отличие от парадокса Рассела, парадокса Кантора, парадокса Бурали Форти, где при помощи логически верных выводов… … Википедия
Изоморфизм графов — В теории графов изоморфизмом графов и называется биекция между множествами вершин графов такая, что любые две вершины и графа смежны, тогда и только тогда, когда вершины … Википедия
Парадокс Скулема — представляет собой рассуждение, связанное с использованием теоремы Лёвенгейма Скулема для аксиоматической теории множеств. В отличие от парадокса Рассела, парадокса Кантора, парадокса Бурали Форти, где при помощи логически верных выводов… … Википедия
Взаимно однозначное отображение
Функция 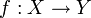
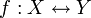
Биекцию также называют взаимно однозначным отображением. Множества, для которых существует биекция, называются равномощными.
Содержание
Примеры
Свойства
Использование модели
В информатике
Организация связи «один к одному» между таблицами реляционной БД на основе первичных ключей
См. также
Литература
Полезное
Смотреть что такое «Взаимно однозначное отображение» в других словарях:
взаимно-однозначное отображение — взаимно однозначное соответствие — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы взаимно однозначное соответствие EN one to one mapping … Справочник технического переводчика
взаимно однозначное отображение — — [[http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23]] Тематики защита информации EN one to one mapping … Справочник технического переводчика
Взаимно-однозначное отображение — Биективная функция. Функция называется биекцией (и обозначается ), если она: Переводит разные элементы множества X в разные элементы множества Y (инъективность). Иными словами … Википедия
Взаимно однозначное соответствие — (математическое) такое соответствие между элементами двух множеств, при котором каждому элементу первого множества соответствует один определённый элемент второго множества, а каждому элементу второго множества один определённый элемент… … Большая советская энциклопедия
ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ — соответствие между элементами двух множеств, при к ром каждому элементу первого множества соответствует единственный элемент второго множества, причем разным элементам первого множества соответствуют разные элементы второго и каждый элемент… … Математическая энциклопедия
Отображение — (матем.) множества А в множество В, соответствие, в силу которого каждому элементу х множества А соответствует определённый элемент у = f (x) множества В, называют образом элемента х (элемент х называют прообразом элемента у). Иногда под… … Большая советская энциклопедия
отображение — Логическая связь набора значений (например, сетевых адресов в одной сети) с объектами другого набора (например, адресами в другой сети). [http://www.lexikon.ru/dict/net/index.html] отображение С самой общей точки зрения это правило, по которому… … Справочник технического переводчика
Отображение — [mapping, transformation] с самой общей точки зрения это правило, по которому элементам одного множества ставятся в соответствие элементы другого множества. Поэтому иногда говорят, что отображение это кортеж, состоящий из трех элементов:… … Экономико-математический словарь
Отображение — [mapping, transformation] с самой общей точки зрения это правило, по которому элементам одного множества ставятся в соответствие элементы другого множества. Поэтому иногда говорят, что отображение это кортеж, состоящий из трех элементов:… … Экономико-математический словарь
ФАКТОРНОЕ ОТОБРАЖЕНИЕ — отображение f то пологич. пространства Xна топологич. пространство Y, при к ром множество открыто в пространстве Yв том и только том случае, если его прообраз f 1v открыт в пространстве X. Если дацрэ отображение f топологич. пространства Xна… … Математическая энциклопедия
Инъективная несюръективная функция (инъекция, а не биекция)
Инъективная сюръективная функция ( биекция )
Неинъективная сюръективная функция (сюръекция, а не биекция)
Неинъективная несюръективная функция (также не биекция)
СОДЕРЖАНИЕ
Определение
Чтобы пара между X и Y (где Y не обязательно отличаться от X ) была биекцией, должны выполняться четыре свойства:
Примеры
Состав бейсбольной или крикетной команды
Места и студенты класса
В классе есть определенное количество мест. Группа студентов входит в комнату, и инструктор просит их сесть. Быстро осмотрев комнату, инструктор заявляет, что существует взаимное соответствие между набором студентов и набором сидений, где каждый студент сопоставляется с сиденьем, на котором они сидят. Что наблюдал преподаватель, чтобы прийти к такому выводу было это:
Инструктор смог сделать вывод, что мест было столько же, сколько и студентов, не считая ни одного набора.
Еще математические примеры и некоторые не-примеры
Перевернутые
В кратких математических обозначениях функция f : X → Y биективна тогда и только тогда, когда она удовлетворяет условию
для каждого y в Y существует единственный x в X с y = f ( x ).
Продолжая пример с расстановкой бейсбольных битов, определяемая функция принимает в качестве входных данных имя одного из игроков и выводит позицию этого игрока в порядке битья. Поскольку эта функция является биекцией, у нее есть обратная функция, которая принимает в качестве входных данных позицию в порядке отбивания и выводит игрока, который будет отбивать эту позицию.
Сочинение
Мощность
Характеристики
Теория категорий
Обобщение на частичные функции
Смотрите также
Примечания
использованная литература
Эта тема является базовой концепцией теории множеств и может быть найдена в любом тексте, который включает введение в теорию множеств. Почти все тексты, посвященные введению в написание доказательств, будут включать раздел по теории множеств, поэтому эту тему можно найти в любом из них: