Что такое взаимно однозначное соответствие множеств

Взаимно однозначное соответствие

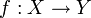
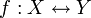
Функция называется биекцией (и обозначается ), если она:

Биекцию также называют взаимно однозначным отображением. Множества, для которых существует биекция, называются равномощными.

Содержание

Примеры

Свойства

Использование модели

В информатике

Организация связи «один к одному» между таблицами реляционной БД на основе первичных ключей

См. также

Литература

Полезное

Смотреть что такое «Взаимно однозначное соответствие» в других словарях:

ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ — такое соответствие между элементами двух множеств, при котором каждому элементу первого множества соответствует один определенный элемент второго множества, а каждому элементу второго множества один определенный элемент первого множества … Большой Энциклопедический словарь

взаимно однозначное соответствие — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN bijection … Справочник технического переводчика

взаимно-однозначное соответствие — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN one one mappingone to one correspondenceone to one dependence … Справочник технического переводчика

взаимно однозначное соответствие — такое соответствие между элементами двух множеств, при котором каждому элементу первого множества соответствует один определённый элемент второго множества, а каждому элементу второго множества один определённый элемент первого множества. * * *… … Энциклопедический словарь

ВЗАИМНО-ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ — [или одно однозначное; сокращенно: (1–1) – соответствие] – одно из основных понятий теорий множеств (см. Множеств теория); частный случай понятия функции. Два множества A и B находятся в отношении В. о. с, если каждому элементу множества А… … Философская энциклопедия

взаимно однозначное соответствие — ▲ соответствие (между) ↑ взаимно, определенный ▼ отпечаток (рельефа), подобный … Идеографический словарь русского языка

ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ — соответствие между элементами двух множеств, при к ром каждому элементу первого множества соответствует единственный элемент второго множества, причем разным элементам первого множества соответствуют разные элементы второго и каждый элемент… … Математическая энциклопедия

Взаимно однозначное соответствие — (математическое) такое соответствие между элементами двух множеств, при котором каждому элементу первого множества соответствует один определённый элемент второго множества, а каждому элементу второго множества один определённый элемент… … Большая советская энциклопедия

ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ — такое соответствие между элементами двух множеств, при к ром каждому элементу первого множества соответствует один определ. элемент второго множества, а каждому элементу второго множества один определ. элемент первого множества … Естествознание. Энциклопедический словарь

взаимно-однозначное отображение — взаимно однозначное соответствие — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы взаимно однозначное соответствие EN one to one mapping … Справочник технического переводчика

Источник

Математика

Множества и операции. Понятие множества.

Взаимно однозначное соответствие между двумя множествами

Разложим наши яблоки, хотя бы на столе, и попробуем положить против каждого яблока пр груше. Возможны три случая (рис. 2).

Первый случай: против каждого яблока окажется груша, и при этом не только все яблоки, но и все груши окажутся разложенными. В этом случае, очевидно, у нас столько же яблок, сколько и груш.

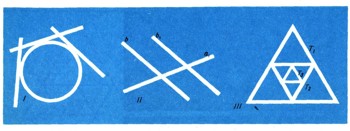
В математике можно найти многочисленные примеры взаимно однозначных соответствий. Например, каждой вершине треугольника или тетраэдра соответствует противоположная этой вершине сторона или грань. Таким образом, установлено взаимно однозначное соответствие между множеством всех вершин треугольника (тетраэдра) и множеством всех его сторон (граней). Множество всех сторон правильного многоугольника находится во взаимно однозначном соответствии с множеством всех перпендикуляров, которые опущены на эти стороны из центра правильного многоугольника. Множество всех боковых граней пирамиды находится во взаимно однозначном соответствии с множеством апофем этой пирамиды и т. д.

Да, есть и такой музей. Часов там много всяких: старинных и современных, механических и электрических, огромных и крошечных, с боем и без боя, с циферблатом и без циферблата.

Ответы и решения

Ответ. 1000000000=10 9 =(2*5) 9 =2 9 *5 9 = 51,2*1953126. 1 000 000 000 000 000 000 = 10 18 = 2 18 * 5 18 = 262 144 * 3 814 697 265 625. каждый из которых, кроме первого, вписан в предыдущий (рис. 3, III). Множество всех этих треугольников обозначим через X. Каждый треугольник получил определенное натуральное число п в качестве своего номера.

Номером треугольника Т_n является натуральное число п. Этим, очевидно, установлено взаимно однозначное соответствие между множеством X наших треугольников и множеством всех натуральных чисел.

Источник

Эквивалентные множества

Мощность конечного множества

Мощностью конечного множества называют число элементов этого множества.

В общем случае мощность множества A обозначают |A|.

Для конечных множеств чаще встречается обозначение n(A).

Конечные множества легко сравнивать по мощности.

Если n(A) = n(B), то конечные множества A и B равномощны.

Например: Мощность множества A= <1;3;5;7>равна n(A)=4.

Мощность множества B = <-3;13;2;4>равна n(B) = 4.

Множества A и B равномощны.

Взаимно однозначное соответствие двух множеств

1) каждому элементу множества A соответствует только один элемент множества B;

2) каждый элемент множества B при этом соответствует некоторому элементу множества A;

3) разным элементам множества A соответствуют разные элементы множества B.

Каждый раз, когда мы «считаем» множество каких-то объектов, мы устанавливаем взаимно однозначно соответствие между этим множеством и подмножеством натуральных чисел от 1 до некоторого n.

С этой точки зрения утверждение

«У Толи три друга: Вася, Коля и Петя» выглядит как соответствие:

Эквивалентность

Такой подход даёт нам возможность сравнивать по мощности не только конечные, но и бесконечные (!) множества.

Сравним мощности множеств натуральных и натуральных чётных чисел:

Для мощности натуральных чисел используется специальное обозначение:

Счётные и несчётные множества

Чтобы доказать счётность множества достаточно придумать правило, по которому нумеруются его элементы.

Докажем, что множество целых чисел счётно.

Что и требовалось доказать.

Таким образом, множество отрезка [0;1]оказывается мощнее всего множества натуральных чисел.

Любой отрезок [a;b] и отрезок [0;1] эквивалентны.

Мощность любого действительного отрезка равна мощности континуума.

Чтобы доказать несчётность множества, нужно показать, что нет таких правил, по которым можно его посчитать. Это значительно сложнее, чем доказать счётность.

Примеры

Пример 1. Среди данных конечных множеств укажите пары эквивалентных:

Запишем с помощью перечисления:

$A \sim B, B \sim C, A \sim C$

В каждый треугольник можно вписать окружность, и притом только одну. Условие единственности (1) выполняется.

Вокруг каждой окружности можно описать бесконечное количество правильных треугольников, поворачивая их на некоторый угол относительно центра окружности.

Условие (2) не выполняется.

Соответствие не является взаимно однозначным.

Пример 3. Постройте взаимно однозначное соответствие между отрезком [0;1] и отрезком [2;7] с помощью линейной функции.

Искомая функция имеет вид y = kx+b, где

Прямая проходит через две точки: A(0;2),B(1;7).

Прямая проходит через две точки: A(0;a),B(1;b). Уравнение прямой:

Источник

Что такое взаимно однозначное соответствие множеств

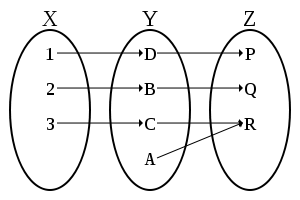
Пример 5. Поставим в соответствие каждой точке квадрата ее проекцию на основание. Получим отображение квадрата на отрезок. Полным прообразом каждой точки основания будет множество всех точек квадрата, лежащих на перпендикуляре к основанию, восстановленном в данной его точке.

Примеры 4 и 5 показывают, что при отображении множества X в Y, с одной стороны, некоторые элементы из Y могут вовсе не иметь прообразов, а, с другой стороны, могут быть элементы, имеющие несколько (даже бесконечно много) прообразов. Если нет ни того, ни другого, то отображение называется взаимно однозначным. Таким образом, приходим к следующему определению:

Определение. Взаимно однозначным соответствием между множествами X и Y (или отображением X на Y) называется соответствие (соответственно, отображение), обладающее следующими тремя свойствами: 1) каждому элементу множества X соответствует один и только один элемент множества Y; 2) двум различным элементам множества X всегда соответствуют два различных элемента множества Y; 3) всякий элемент множества Y соответствует хотя бы одному элементу множества X.

Заметим, что первые два свойства дают взаимно однозначные отображения X на некоторое подмножество Y. В этом случае говорят о взаимно однозначном отображении X в Y.

Определение. Два множества X и Y, между которыми можно установить взаимно однозначное соответствие, называются равномощными (или эквивалентными), что обозначается символом .

О равномощных множествах говорят также, что они имеют одинаковую мощность. Условимся считать, что пустое множество равномощно только самому себе.

Замечание. Выше мы дали определение понятия равномощности, но не понятие мощности. Можно сказать, что мощность есть то общее, что имеется у всех равномощных между собой множеств. Впрочем, всюду достаточно понятие равномощности.

Источник

Лекция17. Взаимно-однозначные соответствия

1. Взаимно-однозначные соответствия. Понятие взаимно однозначного отображения множества Х на множество Y.

2. Равномощные множества. Способы установления равномощности множеств. Счетные и несчетные множества.

Взаимно однозначные соответствия. Понятие взаимно однозначного отображения множества Х на множество Y

В математике изучают различные виды соответствий. Это не слу­чайно, поскольку взаимосвязи, существующие в окружающем нас мире, многообразны. Для учителя, обучающего математике младших школьников, особую значимость имеют взаимно однозначные соот­ветствия.

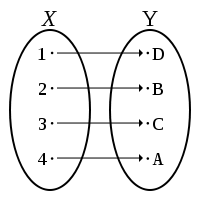
Определение. Взаимно однозначным соответствием между множествами X и Y называется такое соответствие, при кото­ром каждому элементу множества X сопоставляется единст­венный элемент множества Y и каждый элемент множества Y соответствует только одному элементу множества X.

Рассмотрим примеры взаимно однозначных соответствий.

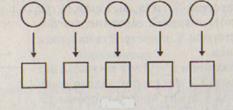
Рис. 76

Это соответствие взаимно однозначное, так как каждому кружку из множества X сопоставляется единственный квадрат из множества Y и каждый квадрат из Y соответствует только одному кружку из множества X.

В математике взаимно однозначное соответствие между множествами X и Y часто называют взаимно однозначным отображение множества X на множество Y.

Понятие взаимно однозначного соответствия позволяет определитьотношение равномощности множеств.

Дата добавления: 2016-05-11 ; просмотров: 2031 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник