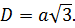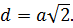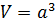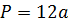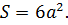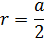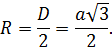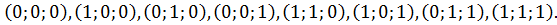Что такое боковые ребра куба

Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.

Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:

многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;

прямая призма, все грани которой есть квадраты;

прямоугольный параллелепипед, все рёбра которого равны.

Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.

Элементы куба

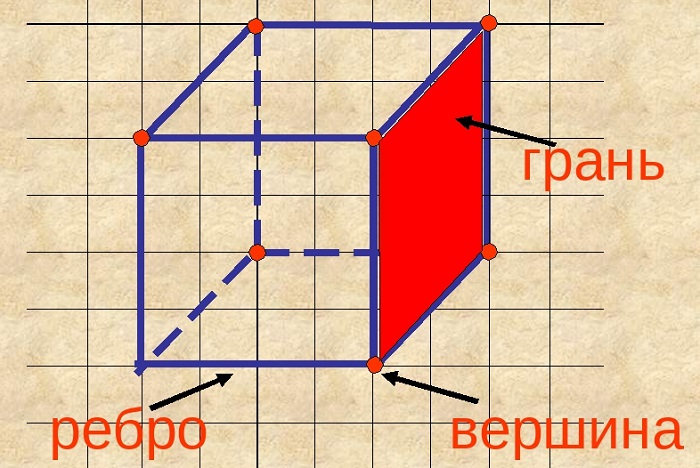
Основными элементами многогранника считаются грани, рёбра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.

Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.

Грани куба попарно перпендикулярны, являются квадратами, равны между собой.

Ребро

Линии пересечения сторон называются рёбрами.

Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.

Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.

Вершина

Точки пересечения рёбер называются вершинами. Их число равно восьми.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.

Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.

Центр куба

Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.

Это есть центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.

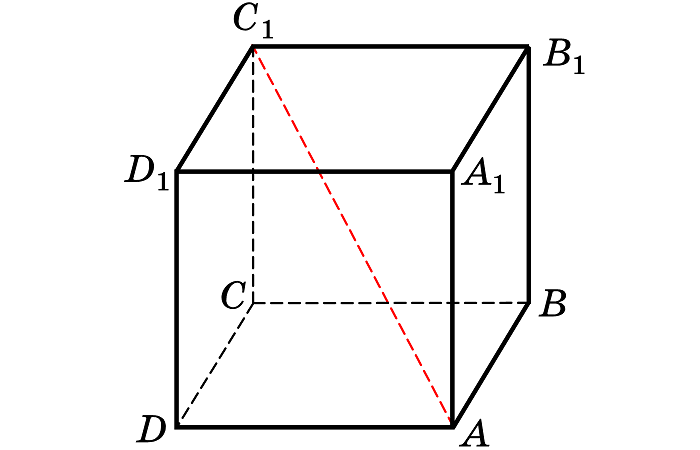
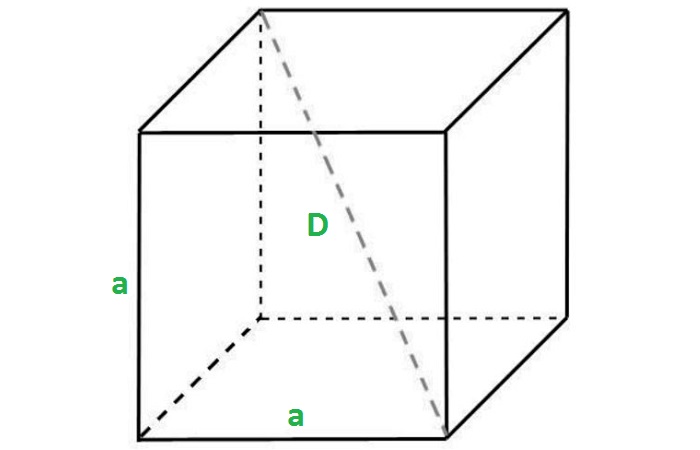
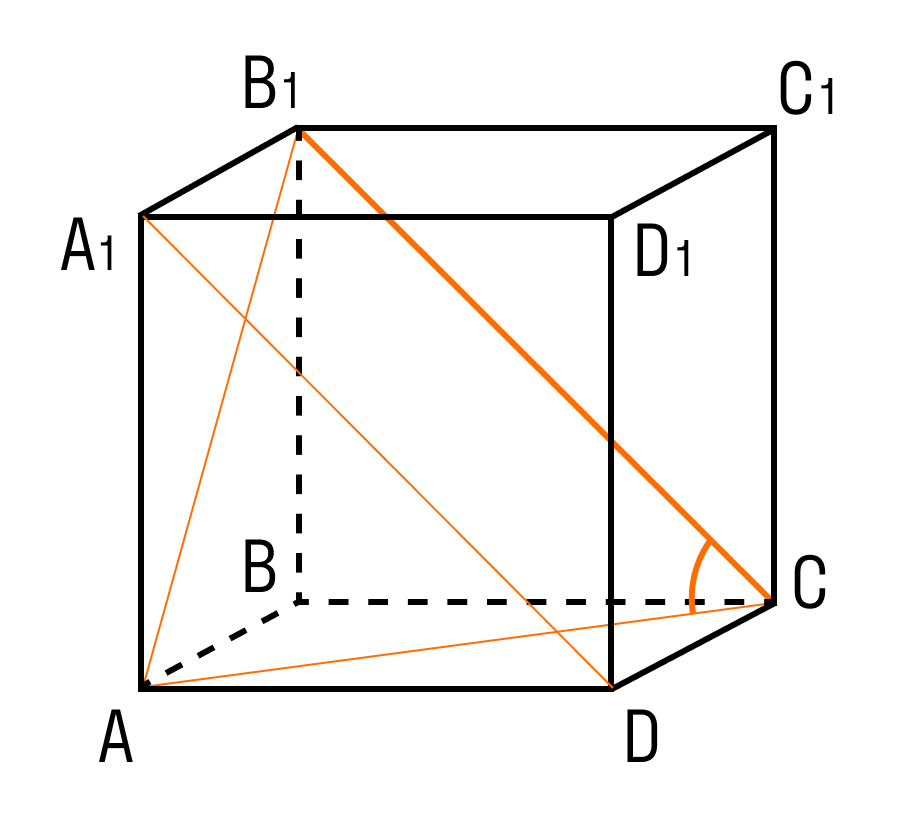
Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.

Все диагонали куба равны между собой и точкой пересечения делятся пополам.

Диагональ грани куба

Длина диагонали грани в √2 раз больше ребра, то есть:

Эта формула доказывается также с помощью теоремы Пифагора.

Объем куба

Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:

Периметр куба

Сумма длин всех рёбер равна:

Площадь поверхности

Сумма площадей всех граней называется площадью поверхности куба. Она равна:

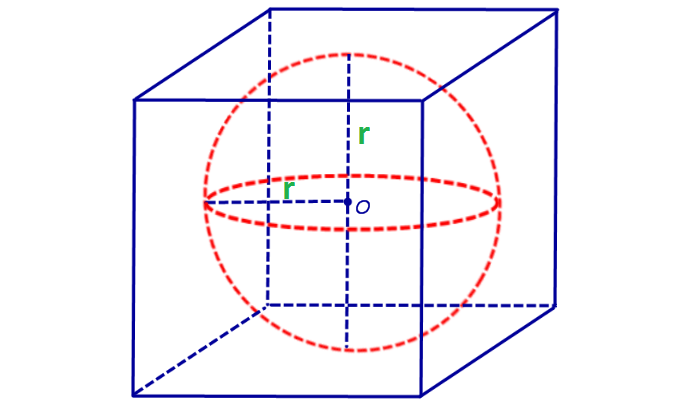
Сфера, вписанная в куб

Такая сфера имеет центр, совпадающий с центром куба.

Радиус равен половине ребра:

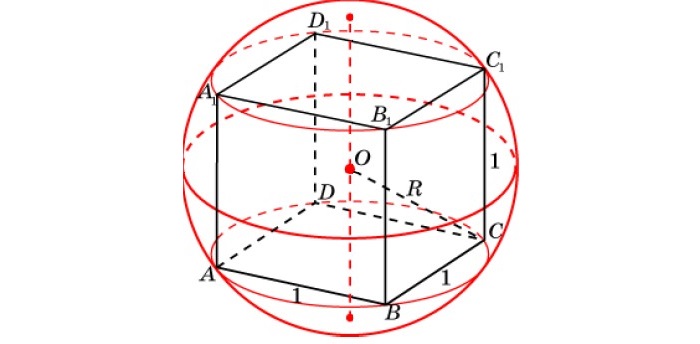
Сфера, описанная вокруг куба

Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:

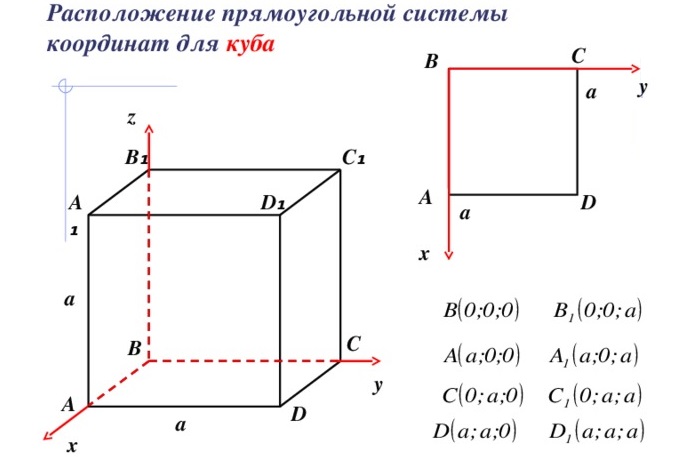
Координаты вершин куба

В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.

Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:

Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).

Свойства куба

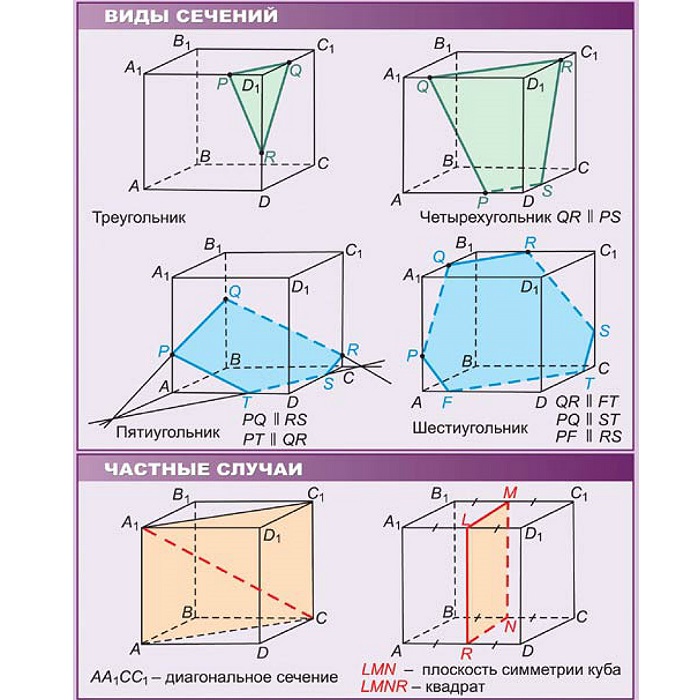
Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.

Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.

у куба все грани равны, являются квадратами;

у куба все рёбра равны;

один центр и несколько осей симметрии.

Источник

Куб — свойства, виды и формулы

Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.

Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:

многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;

прямая призма, все грани которой есть квадраты;

прямоугольный параллелепипед, все рёбра которого равны.

Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.

Элементы куба

Основными элементами многогранника считаются грани, рёбра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.

Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.

Грани куба попарно перпендикулярны, являются квадратами, равны между собой.

Ребро

Линии пересечения сторон называются рёбрами.

Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.

Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.

Вершина

Точки пересечения рёбер называются вершинами. Их число равно восьми.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.

Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.

Центр куба

Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.

Это есть центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.

Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.

Диагональ куба — одна из осей симметрии.

Все диагонали куба равны между собой и точкой пересечения делятся пополам.

Диагональ грани куба

Длина диагонали грани в √2 раз больше ребра, то есть:

Эта формула доказывается также с помощью теоремы Пифагора.

Объем куба

Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:

Периметр куба

Сумма длин всех рёбер равна:

Площадь поверхности

Сумма площадей всех граней называется площадью поверхности куба. Она равна:

Сфера, вписанная в куб

Такая сфера имеет центр, совпадающий с центром куба.

Радиус равен половине ребра:

Сфера, описанная вокруг куба

Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:

Координаты вершин куба

В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.

Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:

Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).

Свойства куба

Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.

Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.

у куба все грани равны, являются квадратами;

у куба все рёбра равны;

один центр и несколько осей симметрии.

Источник

Прямоугольный параллелепипед. Что это такое?

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.

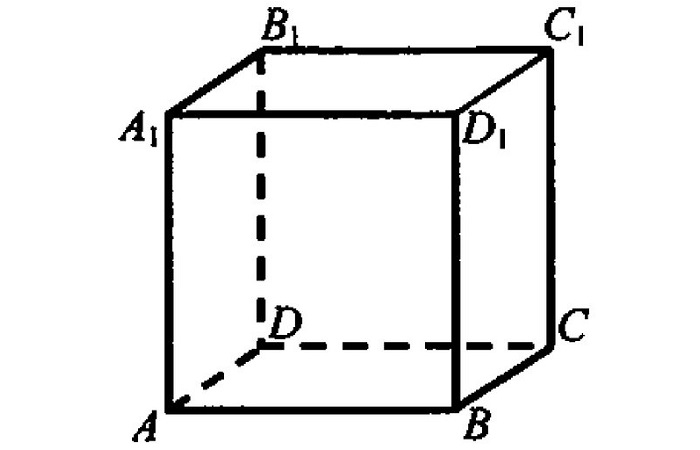
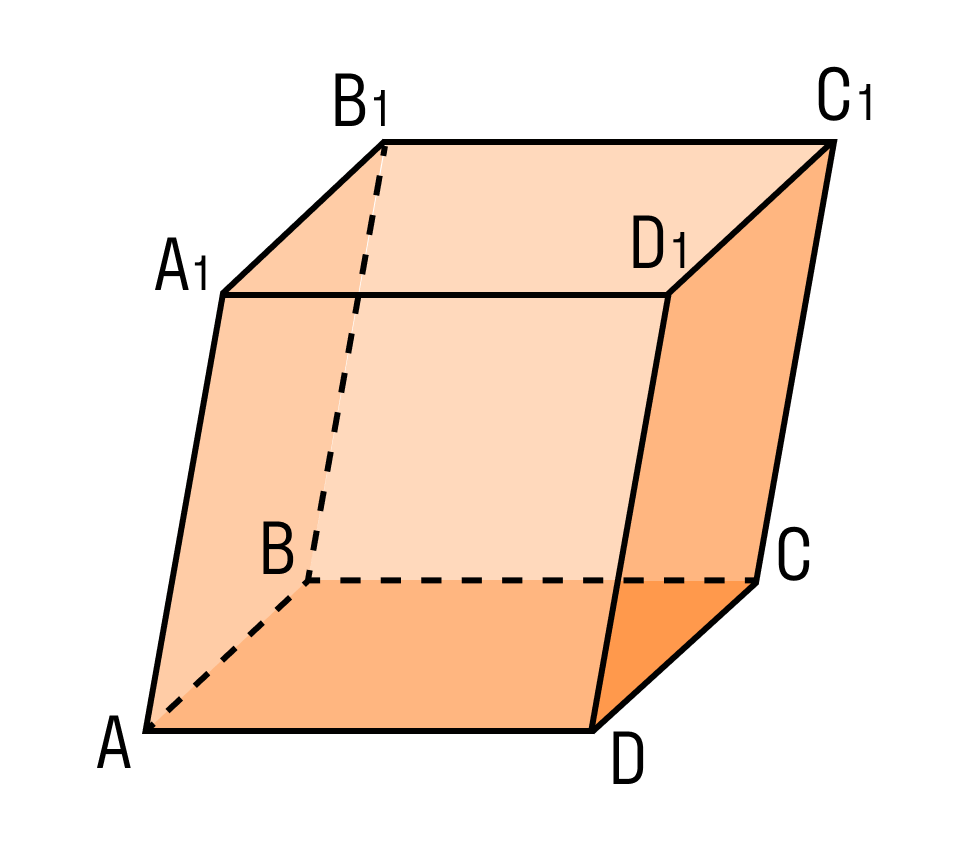
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

На рисунке два параллелограмма АВСD и A₁B₁C₁D₁. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA₁, ВB₁, CC₁, DD₁ параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

Параллелепипед — это:

Правильный параллелепипед на то и правильный, что два его измерения равны. Две грани такого правильного параллелепипеда — квадраты.

Свойства параллелепипеда

Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.

Вот 4 свойства параллелепипеда, которые необходимо запомнить:

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

Свойства прямого параллелепипеда:

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

Прямоугольный параллелепипед

Определение прямоугольного параллелепипеда:

Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.

Свойства прямоугольного параллелепипеда

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.

Формулы прямоугольного параллелепипеда:

Диагонали прямоугольного параллелепипеда: теорема

Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.

Если есть теорема, нужно ее доказать. (с) Пифагор

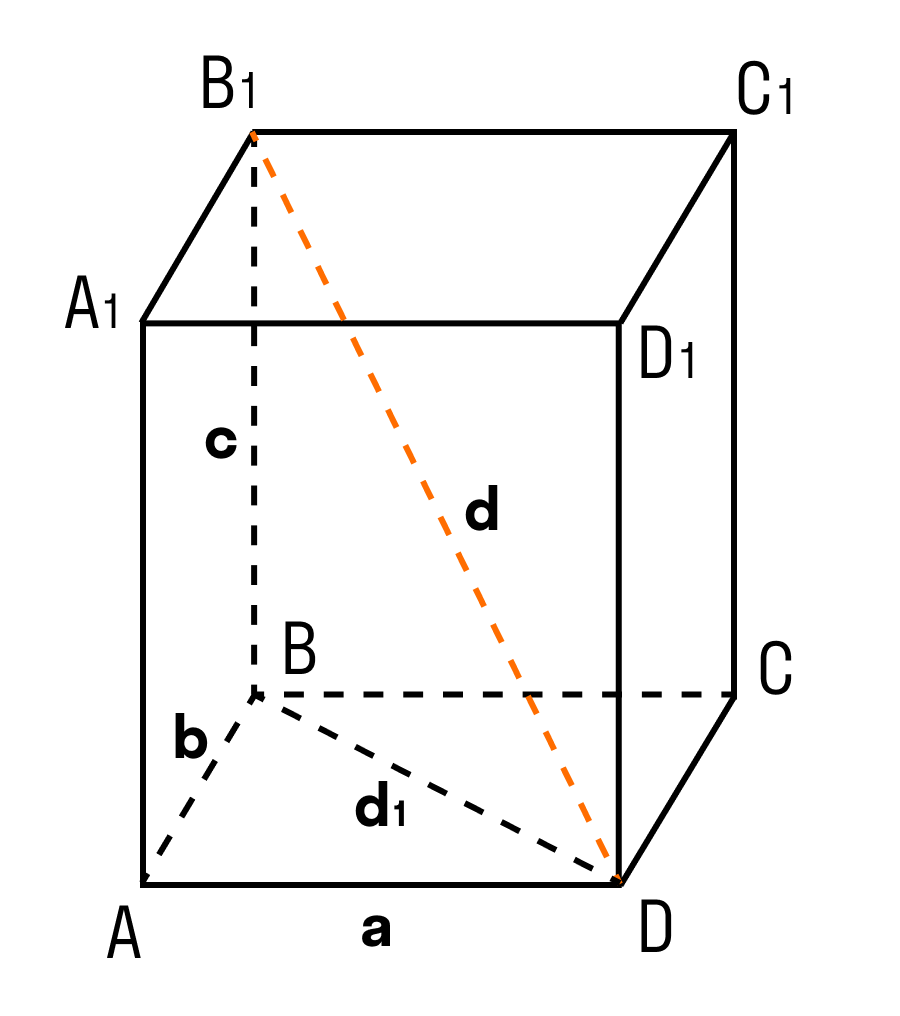
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.

Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Доказать теорему.

Доказательство теоремы:

Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.

Все грани прямоугольного параллелепипеда — прямоугольники.

ΔABD: ∠BAD = 90°, по теореме Пифагора

ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора

d² = a² + b² + c²

Доказанная теорема — пространственная теорема Пифагора.

У нас есть отличные дополнительные онлайн занятия по математике для учеников с 1 по 11 классы, записывайся!

Куб: определение, свойства и формулы

Кубом называется прямоугольный параллелепипед, все три измерения которого равны.

Каждая грань куба — это квадрат.

Свойства куба:

Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.

Формулы куба:

Решение задач

Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.

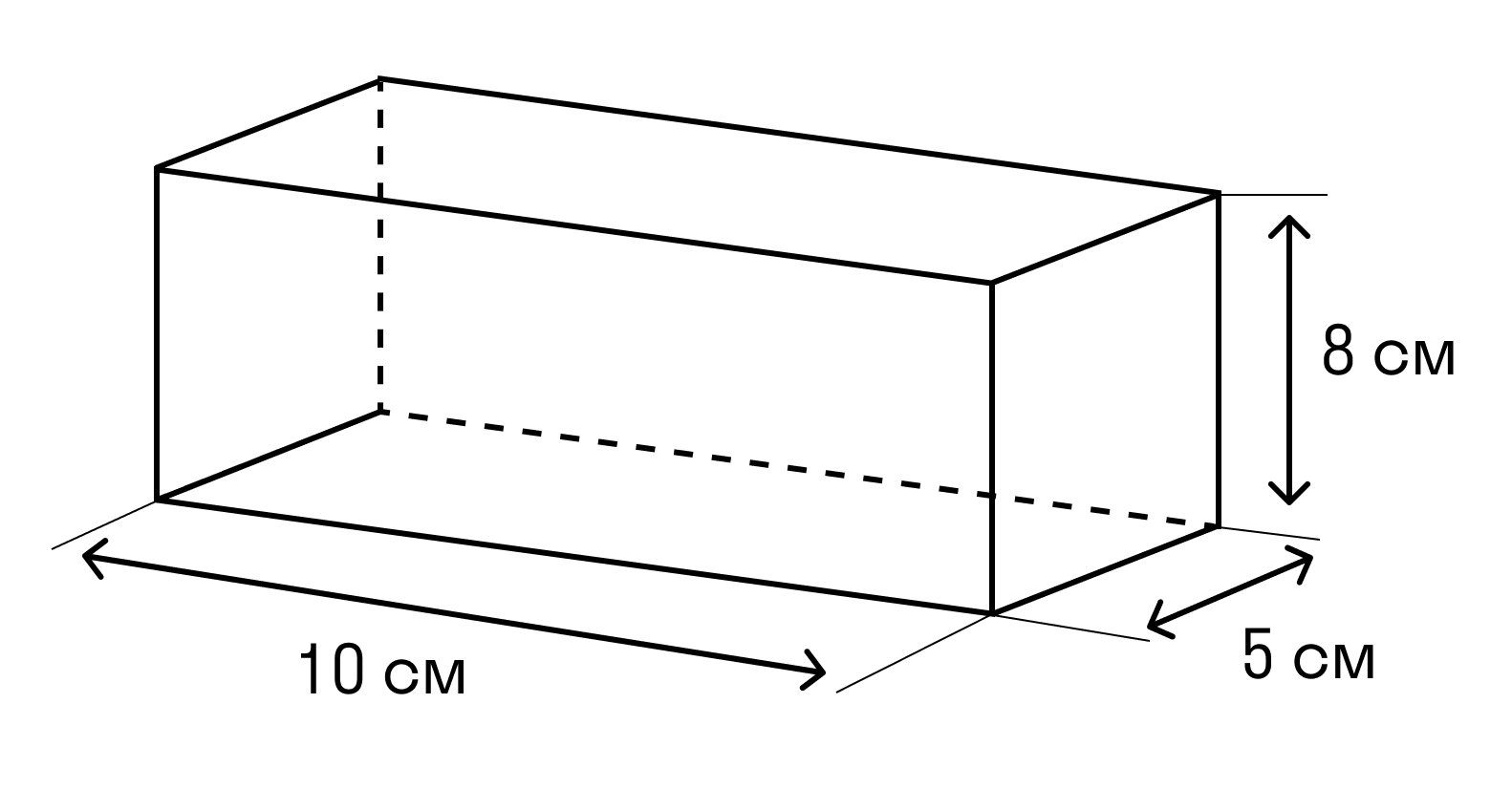
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.

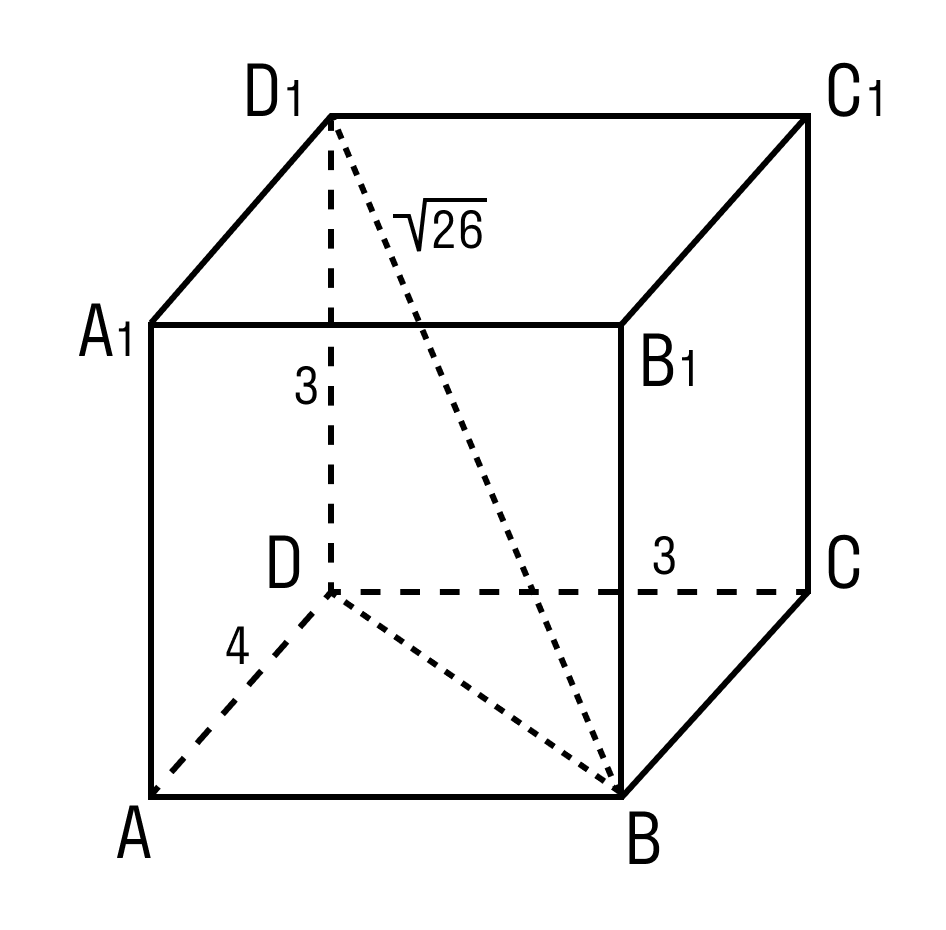
Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Нужно найти длину ребра A₁B₁.

В фокусе внимания треугольник BDD1.
Угол D = 90°. Против равных сторон лежат равные углы.

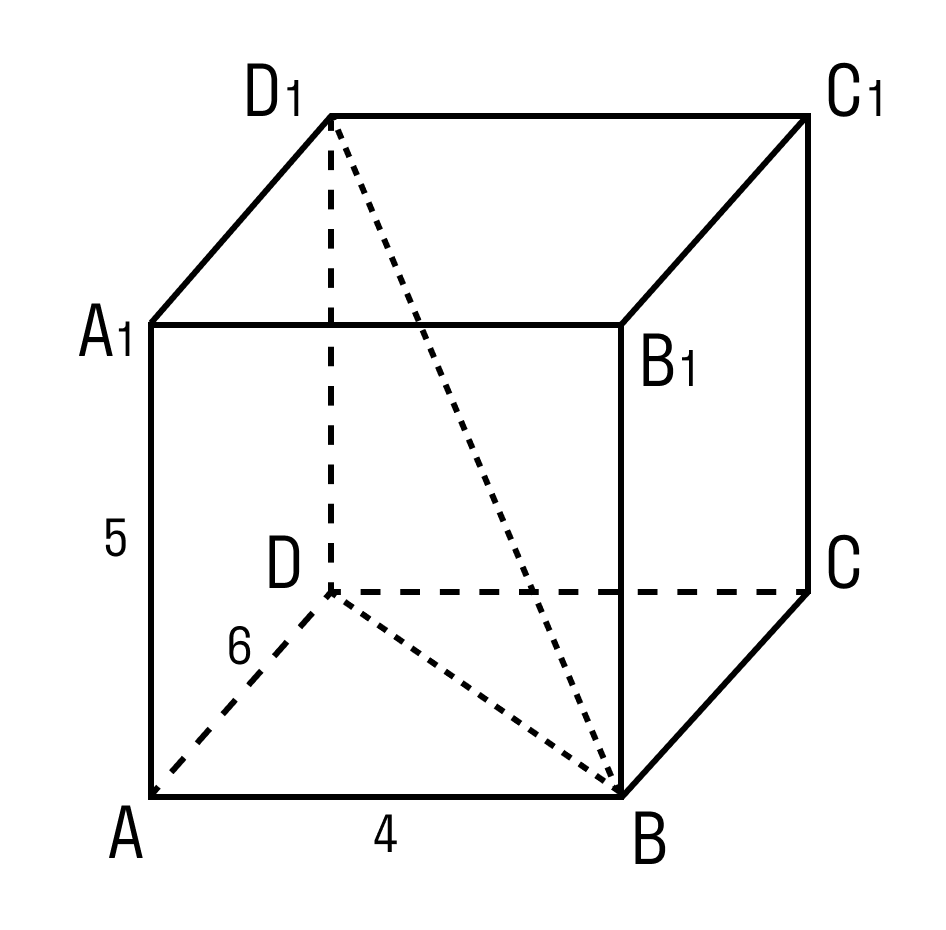
Задачка 3. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AB = 4
AD = 6
AA₁= 5
Нужно найти отрезок BD₁.

В треугольнике ADB угол A = 90°.

По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD₁ угол D = 90°.
BD₁ 2 = 52 + 25 = 77.

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

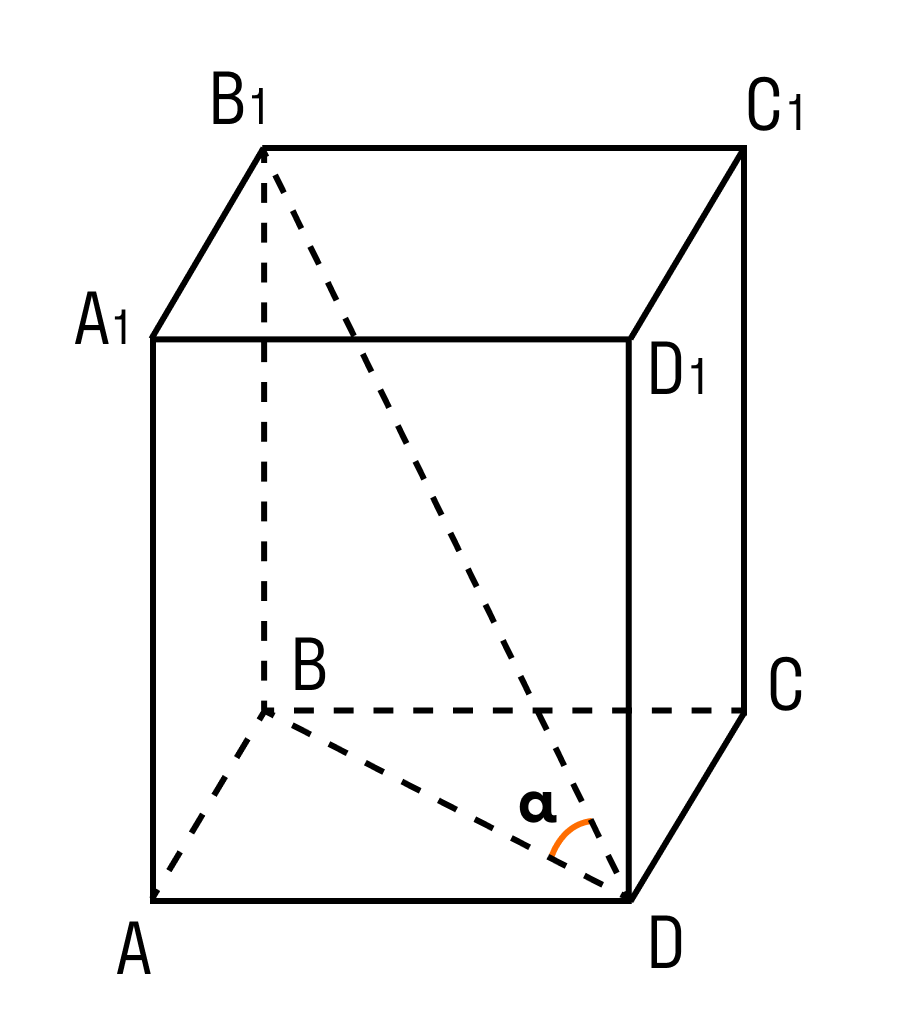
Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Вычислите длину ребра AA₁.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

Источник

Параллелепипед (ЕГЭ 2022)

Что за слово такое мудреное – «параллелепипед»? Что за многогранник скрывается за этим словом?

Что-то должно быть связано с параллельностью, не правда ли?

Читай статью, смотри вебинар и ты все про него будешь знать!

Параллелепипед — коротко о главном

Параллелепипед — это четырехугольная призма (многогранник с \( \displaystyle 6\) гранями), все грани которой — параллелограммы.

Прямой параллелепипед —это параллелепипед, у которого \( \displaystyle 4\) боковые грани — прямоугольники.

Прямоугольный параллелепипед — параллелепипед, у которого все грани — прямоугольники

Куб — параллелепипед, у которого все грани квадраты.

Высота параллелепипеда – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.

Свойства параллелепипеда

Параллелепипед — подробнее

Параллелепипед – многоугольник, образованный пересечением трех пар параллельных плоскостей.

Если слишком сложно, просто посмотри на картинку.

Какую фигуру из планиметрии (геометрии с «плоскими» фигурами) напоминает параллелепипед?

Немного похоже на параллелограмм, правда? Только «потолще» и слово подлиннее.

Далее смотри на картинки, запоминай и не путай!

Высота – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.

Та грань, на которую опущена высота, называется основанием.

Свойства параллелепипеда

Внимание: передняя и задняя грани параллелепипеда равны, верхняя и нижняя – тоже равны, но не равны (не обязаны быть равны) передняя и верхняя грани – потому что они не противоположные, а смежные.

Прямой параллелепипед

Прямым называется параллелепипед, у которого боковые ребра перпендикулярны основанию.

У прямого параллелепипеда в основании – параллелограмм, а боковые грани – прямоугольники.

Прямоугольный параллелепипед

Прямоугольным называется параллелепипед, у которого в основании прямоугольник, а боковые ребра перпендикулярны основанию.

Это такая обувная коробка:

У прямоугольного параллелепипеда все грани – прямоугольники.

Давай-ка теперь выведем одну интересную формулу для диагонали прямоугольного параллелепипеда.

Диагональ прямоугольного параллелепипеда равна сумме квадратов его измерений.\( \displaystyle <^<2>>=<^<2>>+<^<2>>+<^<2>>\).

Видишь, как красиво? На теорему Пифагора похоже, правда? И формула эта как раз и получается из теоремы Пифагора.

Источник