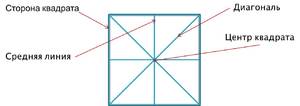
Что такое диагональ квадрата 4 класс
Формулы и способы как находить диагональ квадрата
При решении задач по школьной математике часто требуется определить, чему равняется диагональ заданного квадрата. При кажущейся некоторой сложности, эта задача является весьма простой и имеет несколько несложных способов решения. Рассмотрим их, для начала введём некоторые понятия и определения.
Определения и соглашения
Как понятно из вышеизложенного, у квадрата только две диагонали. Поскольку квадрат является прямоугольником и сохраняет его свойства, то они равны между собой. Рассмотрим различные методы нахождения её длины.
Вычисление диагонали квадрата по известной стороне
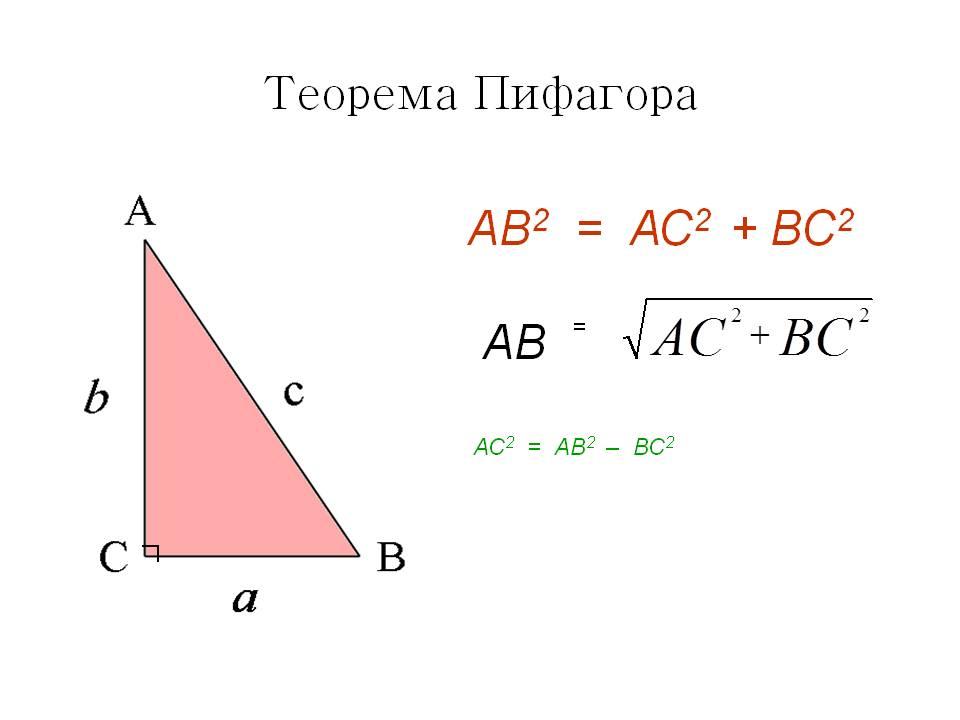
Самым простым способом является вычисление диагонали, если известна сторона квадрата. Здесь действует широко известная теорема Пифагора для прямоугольных треугольников. Запишем эту формулу: c^2 = a^2+b^2.
Отметим, что в нашем случае диагональ квадрата есть гипотенуза треугольника с равными катетами. Перепишем формулу исходя из наших условий: d^2 = a^2+a^2. Преобразуем, получим: d^2 = 2*a^2. Следующим шагом извлечём квадратный корень, получится: d = rad2*a. Это и есть наша конечная формула.
Рассмотрим вычисление на примере. Пусть a = 64. Подставим наше значение в формулу. Получим d = 64*rad2. Это и есть ответ.
Вычисление диагонали квадрата по известной площади
Пусть нам дана площадь квадрата, её обозначают латинской буквой S, найдём его диагональ.
Используем свойства прямоугольника и запишем формулу его площади.
S = a*b. Перепишем для b = a. Получим: s = a^2. Отсюда найдём сторону: a = radS. Итак, нам удалось выразить сторону через площадь. Подставим полученное выражение в конечную формулу из предыдущей части. Формула примет вид: d = rad2*a = rad2*radS.
Пример: допустим, площадь равна 32 квадратных метра. Подставим это число. Получим rad2*rad32 = rad2*4*rad2 = 4*2 = 8 метров.
Вычисление диагонали по известному периметру
Пусть нам известен периметр. В дальнейшем его будем записывать латинской буквой P, найдём его d. Воспользуемся свойствами прямоугольника и запишем формулу его периметра.
P = два*(a + b). Перепишем для b = a. У нас получится: P = два*(a + a) = 2*2a = 4*a. Выразим из последней формулы сторону. Имеем: a = P/4. Воспользуемся тем, что: d = rad2*a. Выразим сторону через периметр. Наша формула примет видd = rad2*P/4.
Примере: пусть периметр равен 128 метров. Проведём несложный расчёт. Имеем, rad =d2*128/4 = 32*rad2 метров.
Вычисление по радиусу описанной и вписанной окружности
Ещё один способ, который на само деле очень простой. Радиус описанной окружности будем обозначать латинской буквой R, радиус вписанной окружности будем обозначать латинской буквой r.
Сначала разберёмся с описанной окружностью. В данной ситуации её радиус составляет ровно половину диагонали (это нетрудно убедиться с использованием построения), таким образом: R = 1/2*d. отсюда имеем: d = два*R. Снова поясним наши рассуждения на примере. Пусть R = 45 километров. Получим, d = два*45 = 90 километров.
И, наконец, рассмотрим метод, связанный с радиусом вписанной окружности. Опять-таки из построения чётко видно, что диаметр вписанной окружности равняется стороне квадрата. Таким образом, её радиус вдвое меньше стороны. Запишем это в виде формулы: r = 1/2*a. Отсюда следует, a = 2*r. Снова воспользуемся формулой из первого метода, подставим вместо стороны её выражение через радиус вписанной окружности. Выражение примет вид: d = rad2*a = rad2*2*r.
Ещё раз воспользуемся помощью примера. Пусть r = 98 метров. Тогда имеем, d = rad2*2*98 = 196*rad2.
Заключение
Таким образом, мы рассмотрели в статье пять принципиально различных методов вычисления диагонали квадрата. Если, на первый взгляд, задача казалась сложной, то после проведённых нами рассуждений стало очевидно, что особых проблем здесь нет. Сведём все полученные нами формулы в одну таблицу.
Хочется ещё отметить, что с помощью первой из наших формул очень легко построить отрезок, равный корню квадратному из двух. Для этого строим квадрат со стороной единица, его диагональ и будет равняться искомому отрезку.
Если на полученной диагонали мы построим прямоугольник, используя её как длину, а ширину возьмём равной единице, то получим отрезок равный ещё одному иррациональному числу корень квадратный из трёх.
Продолжая нашу цепочку и далее, мы научимся строить отрезки равные любому иррациональному числу.
Видео
Из видео вы узнаете, как найти диагональ квадрата, если известна его площадь.
Квадрат — определение и свойства
Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.
Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.
Перечислим свойства квадрата:
Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.
Очевидно, радиус окружности равен половине диагонали квадрата.
Диаметр окружности равен стороне квадрата.
Чуть более сложная задача. Нарисуйте окружность, вписанную в данный квадрат, то есть касающуюся всех его сторон. Вы увидите, что диаметр этой окружности равен стороне квадрата.
Считаем стороны клеток равными единице. Четырехугольник — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.
Как посчитать диагональ квадрата? Формула длины диагонали квадрата.
Как посчитать диагональ квадрата?
Безусловно, лучше всего просто запомнить формулу длины диагонали квадрата и пользоваться ею всегда, ведь это гораздо быстрее и удобнее. Особенно это чувствуется при решении задач в буквенном виде, где вместо целых больших подкорневых выражений можно обойтись лишь одним произведением.
Пример
Возьмем, к примеру, квадрат 6 на 6, то есть со стороной, равной шести сантиметрам.
Тогда получим, что С=√А^2+А^2 или С=√2А^2.
Запишем в числовом виде: С =√36 + 36. Получили √72, а это 3√8 или 6√2.
А теперь найдем ту же диагональ, но уже по второму способу: С = А√2 или в числовом виде: 6√2
Другие свойства диагоналей квадрата
Помимо знания того, как найти диагонали квадрата, нужно также знать и их свойства. Основные из них:
Вывод
Вопросом, как посчитать диагонали квадрата, обычно задаются ученики, пропустившие эту тему в школе. Однако такие фундаментальные правила математики должен знать каждый! Желательно решать как можно быстрее, и для этого необходимы знания сокращенных формул. Все это предельно просто и легко, но вместе с тем является базой, необходимой для решения в дальнейшем гораздо более сложных задач. И важную часть этой базы занимает квадрат.
Что такое квадрат: определение и свойства
В данной публикации мы рассмотрим определение и свойства (с рисунками) одной из основных геометрических фигур – квадрата.
Определение квадрата
Свойства квадрата
Свойство 1
Диагонали квадрата равны, расположены под прямым углом друг к другу, в точке пересечения делятся пополам.
Свойство 2
Диагонали квадрата являются биссектрисами его углов. Для рисунке выше:
Свойство 3
Центром описанной вокруг и вписанной в квадрат окружностей является точка пересечения его диагоналей (в нашем случае – E).
При этом радиусы окружностей можно вычислить через длину стороны или диагонали квадрата:
Также, один радиус можно выразить через другой:
Свойство 4
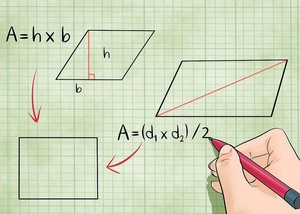
Зная длину стороны или диагонали квадрата, можно найти его площадь или периметр.
Периметр (P) квадрата через сторону:
P = a + a + a + a = 4 ⋅ a
Периметр (P) квадрата через диагональ:
Площадь (S) квадрата через сторону:
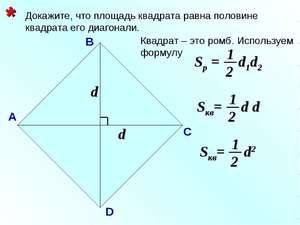
Площадь (S) квадрата через диагональ:
Свойства диагоналей квадрата
Конспект урока математики
Дата проведения: 23. 09.2010 г.
Тема: Свойства диагоналей квадрата.
Тип урока: Расширение знаний о квадрате.
Цели урока:
Оборудование: компьютер, проектор, переносной экран.
Структура урока.
I. Орг. момент. 1 мин.
II. Сообщение темы и целей урока. 1 мин.
III. Устный счет. 5 мин.
IV. Изучение нового материала. 10 мин.
V. Физкультминутка. 2 мин.
VI. Закрепление изученного. 11 мин.
VIII. Домашнее задание. 1 мин.
Ход урока.
I. Орг. момент
Учитель: Встали все правильно. Спинки все выпрямили. Первый ряд – тихонечко сели, второй ряд – тихонечко сели, третий ряд – тихонечко сели.
II. Сообщение темы и целей урока
Учитель: Ребята, сегодня мы с вами продолжим работу с диагоналями, но объектом нашего исследования будет квадрат.
III. Устный счет.
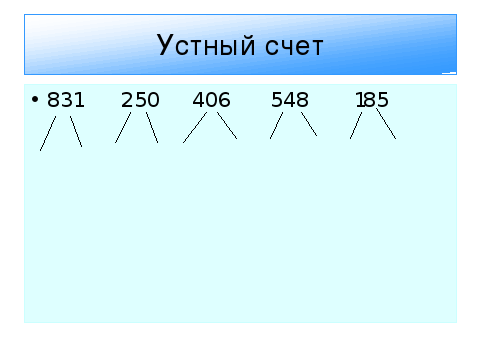
Найдите значения этих выражений.
2. Какие знаки можно поставить вместо снежинок и цифры вместо квадратиков так, чтобы получились верные равенства:
3. Замените суммой разрядных слагаемых следующие числа:
4. Стороны прямоугольника 7см и 5 см. Чему равна площадь квадрата, если периметр его равен периметру прямоугольника?
IV. Изучение нового материала
Учитель: Что такое прямоугольник?
Дети: Прямоугольник –это четырёхугольник, у которого все углы прямые и противоположные стороны равны.
Учитель: Что такое диагональ?
Дети: Диагональ – это прямая линия, соединяющая противоположные углы прямоугольника и расположена под острым углом к его сторонам.
Учитель: Назовите свойства диагоналей прямоугольника.
Дети: 1) Диагонали прямоугольника равны.
2) Все отрезки, которые получаются при пересечении диагоналей прямоугольника, равны.
Учитель: Что такое квадрат?
Дети: Квадрат – это четырехугольник, у которого все углы прямые и все стороны равны.
Учитель: Мы с вами знаем, что диагонали прямоугольника равны. Равны ли будут диагонали квадрата?
Дети: Диагонали квадрата тоже равны, т.к. квадрат – это прямоугольник, у которого все стороны равны.
Учитель: Если квадрат – это прямоугольник, значит и свойства диагоналей такие же.
2) Все отрезки, которые получаются при пересечении диагоналей квадрата, равны.
Ребята у квадрата есть ещё одно особенное свойство, которого у прямоугольника нет.
3) При пересечении диагоналей квадрата получаются четыре прямых угла.
Учитель: А сейчас давайте проверим все эти свойства на рисунке в учебнике.
Откроем учебник на странице 17. Наверху нарисованы 2 квадрата и в них проведены диагонали.
Назовите мне первый квадрат.
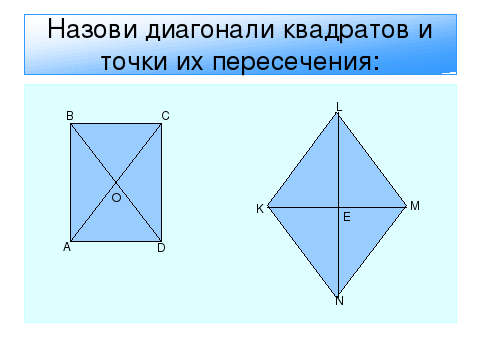
Дети: Первый квадрат АВСD
Учитель: Назовите диагонали квадрата АВСD
Дети: Диагональ BD и СА
Учитель: Что такое точка О?
Дети: Точка пересечения диагоналей.
Учитель: Назовите второй квадрат на рисунке.
Дети: Второй квадрат KLMN
Учитель: Назовите диагонали этого квадрата.
Учитель: Назовите точку пересечения диагоналей
Учитель: Какие углы образуются при пересечении диагоналей?
Дети: Образуются прямые углы. Чтобы проверить, можно подставить линейку и убедиться в этом.
Учитель: Назовите мне эти углы
Дети: KEL, LEM, MEN, NEK
Учитель: А сейчас, ребята, давайте немного отдохнем.
Чудеса на белом свете –
Стали маленькими дети.
А потом все дружно встали,
Великанами вдруг стали.
Флюгер есть теперь у нас,
Ветер справа, ветер слева,
Флюгер вертится умело.
Сначала буду маленьким,
К коленочкам прижмусь.
Потом я вырасту большим,
Учитель: Немного отдохнули, а сейчас давайте выполним № 81
(Дети читают задание. Один человек выполняет на доске, остальные в тетради)
Учитель: Выполняем № 84 (1,2) – на доске, 3,4 – самостоятельно в тетради.
(4 человека выполняют на доске, остальные выполняют в тетрадях).
832:9=92(ост.4) 641:3=213(ост.3) 587:8=73(ост.3) 667:7=94(ост.5)
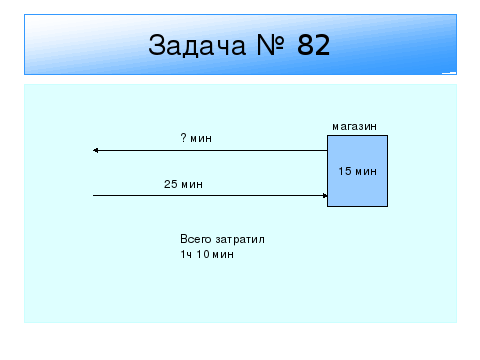
Учитель: Читаем задачу № 82
Сначала скажите, сколько в 1ч минут?
1ч 10 мин переведите в минуты
— получится 70 минут
Можем ли мы сразу ответить на вопрос задачи?
— мы не знаем сколько времени он затратил на поездку в магазин и был в магазине
Как нам узнать это?
— мы к времени, которое затратил мальчик на дорогу в магазин прибавим время, которое он был в магазине
Теперь мы можем узнать, сколько времени мальчик ехал назад
Учитель: Что такое прямоугольник?
Дети: Прямоугольник –это четырёхугольник, у которого все углы прямые и противоположные стороны равны.
Учитель: Назовите свойства диагоналей прямоугольника.
Дети: 1) Диагонали прямоугольника равны.
2) Все отрезки, которые получаются при пересечении диагоналей прямоугольника, равны.
Учитель: Что такое квадрат?
Дети: Квадрат – это четырехугольник, у которого все углы прямые и все стороны равны.
Учитель: Назовите свойства диагоналей квадрата.
2) Все отрезки, которые получаются при пересечении диагоналей квадрата, равны.
Учитель: Молодцы ребята! Вы сегодня хорошо поработали!
Откроем дневники и запишем домашнее задание: №83, №85 стр.17
Урок окончен. Можете идти отдыхать.
Просмотр содержимого документа
«Конспект урока математики 4 кл.»
Конспект урока математики
Тема: Свойства диагоналей квадрата.
Тип урока: Расширение знаний о квадрате.
совершенствовать письменные вычислительные навыки и умение решать задачи;
показать практическую значимость математических знаний для решения задач в повседневной жизни;
обеспечить усвоение учащимися свойств диагоналей квадрата.
развивать умение ясно выражать свои мысли, анализировать, сравнивать, делать выводы и обобщения;
развивать навыки по определению свойств квадрата.
формировать способности к исследованию;
формировать умение наблюдать и анализировать;
воспитывать интерес к предмету.
Оборудование: компьютер, проектор, переносной экран.
Подведение итогов, выставление оценок. 4 мин.
Учитель: Встали все правильно. Спинки все выпрямили. Первый ряд – тихонечко сели, второй ряд – тихонечко сели, третий ряд – тихонечко сели.
II . Сообщение темы и целей урока
Учитель: Ребята, сегодня мы с вами продолжим работу с диагоналями, но объектом нашего исследования будет квадрат.
Найдите значения этих выражений.
2. Какие знаки можно поставить вместо снежинок и цифры вместо квадратиков так, чтобы получились верные равенства:
3. Замените суммой разрядных слагаемых следующие числа:
4. Стороны прямоугольника 7см и 5 см. Чему равна площадь квадрата, если периметр его равен периметру прямоугольника?
IV . Изучение нового материала
Учитель: Что такое прямоугольник?
Дети: Прямоугольник –это четырёхугольник, у которого все углы прямые и противоположные стороны равны.
Учитель: Что такое диагональ?
Дети: Диагональ – это прямая линия, соединяющая противоположные углы прямоугольника и расположена под острым углом к его сторонам.
Учитель: Назовите свойства диагоналей прямоугольника.
Дети: 1) Диагонали прямоугольника равны.
2) Все отрезки, которые получаются при пересечении диагоналей прямоугольника, равны.
Учитель: Что такое квадрат?
Дети: Квадрат – это четырехугольник, у которого все углы прямые и все стороны равны.
Учитель: Мы с вами знаем, что диагонали прямоугольника равны. Равны ли будут диагонали квадрата?
Дети: Диагонали квадрата тоже равны, т.к. квадрат – это прямоугольник, у которого все стороны равны.
Учитель: Если квадрат – это прямоугольник, значит и свойства диагоналей такие же.
Диагонали квадрата равны.
2) Все отрезки, которые получаются при пересечении диагоналей квадрата, равны.
Ребята у квадрата есть ещё одно особенное свойство, которого у прямоугольника нет.
3) При пересечении диагоналей квадрата получаются четыре прямых угла.
Учитель: А сейчас давайте проверим все эти свойства на рисунке в учебнике.
Откроем учебник на странице 17. Наверху нарисованы 2 квадрата и в них проведены диагонали.
Назовите мне первый квадрат.
Дети: Первый квадрат АВС D
Учитель: Назовите диагонали квадрата АВС D
Дети: Диагональ BD и СА
Учитель: Что такое точка О?
Дети: Точка пересечения диагоналей.
Учитель: Назовите второй квадрат на рисунке.
Дети: Второй квадрат KLMN
Учитель: Назовите диагонали этого квадрата.
Учитель: Назовите точку пересечения диагоналей
Учитель: Какие углы образуются при пересечении диагоналей?
Дети: Образуются прямые углы. Чтобы проверить, можно подставить линейку и убедиться в этом.
Учитель: Назовите мне эти углы
Учитель: А сейчас, ребята, давайте немного отдохнем.
Чудеса на белом свете –
Стали маленькими дети.
А потом все дружно встали,
Великанами вдруг стали.
Флюгер есть теперь у нас,
Ветер справа, ветер слева,
Флюгер вертится умело.
Сначала буду маленьким,
К коленочкам прижмусь.
Потом я вырасту большим,
Учитель: Немного отдохнули, а сейчас давайте выполним № 81
(Дети читают задание. Один человек выполняет на доске, остальные в тетради)
Учитель: Выполняем № 84 (1,2) – на доске, 3,4 – самостоятельно в тетради.
(4 человека выполняют на доске, остальные выполняют в тетрадях).
832:9=92(ост.4) 641:3=213(ост.3) 587:8=73(ост.3) 667:7=94(ост.5)
Учитель: Читаем задачу № 82
Сначала скажите, сколько в 1ч минут?
1ч 10 мин переведите в минуты
— получится 70 минут
Можем ли мы сразу ответить на вопрос задачи?
— мы не знаем сколько времени он затратил на поездку в магазин и был в магазине
Как нам узнать это?
— мы к времени, которое затратил мальчик на дорогу в магазин прибавим время, которое он был в магазине
Теперь мы можем узнать, сколько времени мальчик ехал назад
Подведение итогов, выставление оценок.
Учитель: Что такое прямоугольник?
Дети: Прямоугольник –это четырёхугольник, у которого все углы прямые и противоположные стороны равны.
Учитель: Назовите свойства диагоналей прямоугольника.
Дети: 1) Диагонали прямоугольника равны.
2) Все отрезки, которые получаются при пересечении диагоналей прямоугольника, равны.
Учитель: Что такое квадрат?
Дети: Квадрат – это четырехугольник, у которого все углы прямые и все стороны равны.
Учитель: Назовите свойства диагоналей квадрата.
Диагонали квадрата равны.
2) Все отрезки, которые получаются при пересечении диагоналей квадрата, равны.
При пересечении диагоналей квадрата получаются четыре прямых угла.
Учитель: Молодцы ребята! Вы сегодня хорошо поработали!
Откроем дневники и запишем домашнее задание: №83, №85 стр.17
Урок окончен. Можете идти отдыхать.
Просмотр содержимого презентации
«Свойства диагоналей квадрата»


Свойства диагоналей прямоугольника

Свойства диагоналей квадрата
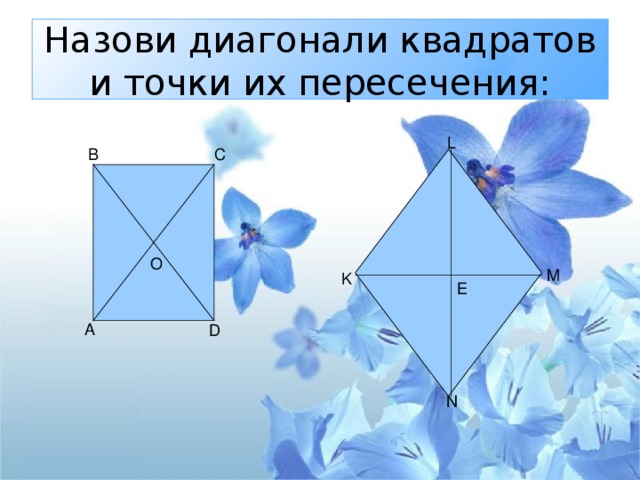
Назови диагонали квадратов и точки их пересечения:
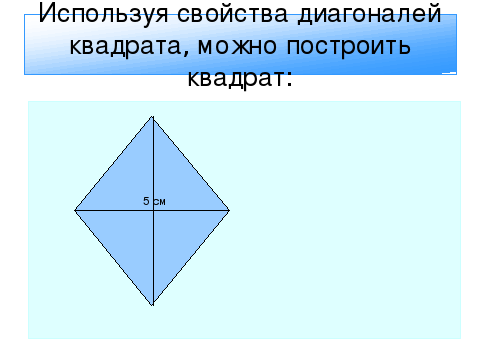
Используя свойства диагоналей квадрата, можно построить квадрат: