Что такое диагональ выпуклого многоугольника
Многоугольник
Определение 1. Многоугольник − замкнутая ломаная линия.
Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:
Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.
Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.
Виды многоугольников
Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с \( \small n \) вершинами называется \( \small n- \)угольником.
  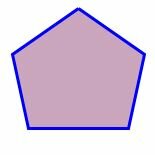  |
На рисунке 1 представлены различные виды многоугольников.
Обозначение многоугольника
Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют \( \small A_1A_2A_3A_4A_5A_6 \) или \( \small A_6A_5A_4A_3A_2A_1 \).
Соседние вершины многоугольника
Вершины многоугольника называются соседними, если они являются концами одной из его сторон.
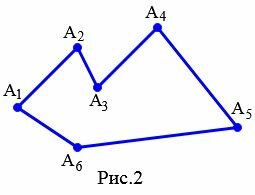 |
На рисунке 2 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)
Смежные стороны многоугольника
Стороны многоугольника называются смежными, если они имеют общую вершину.
На рисунке 2 стороны \( \small A_4A_5 \) и \( \small A_5A_6 \) являются смежными, так как они имеют общую вершину \( \small A_5. \)
Простой многоугольник. Самопересекающийся многоугольник
Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).
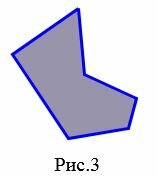 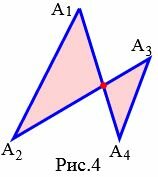 |
На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой многоугольник называется самопересекающийся многоугольник.
Выпуклый многоугольник
Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.
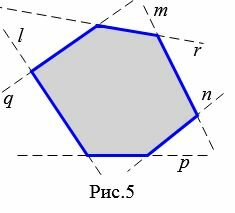 |
На рисунке 5 многоугольник лежит по одну сторону от прямых \( \small m, \ n, \ l, \ p, \ q, \ r\) проходящих через стороны многоугольника.
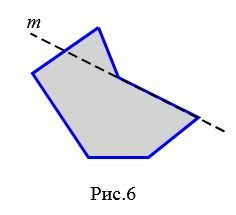 |
На рисунке 6 прямая \( \small m\) делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой \( \small m\). Следовательно многоугольник не является выпуклым.
Правильный многоугольник
Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.
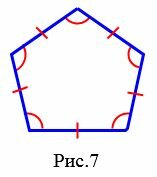 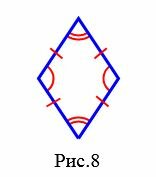 |
На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.
Звездчатый многоугольник
Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.
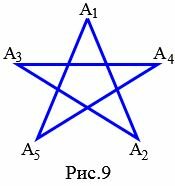 |
На рисунке 9 представлен звездчатый пятиугольник поскольку все углы \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) равны и равны все стороны: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)
Периметр многоугольника
Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника \( \small A_1A_2. A_
Угол многоугольника
Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small A_3 \) на рисунке 2).
Внешний угол многоугольника
Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.
На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине \( \small E. \)
Диагональ многоугольника. Количество диагоналей
Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.
Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:
Сумма углов выпуклого многоугольника
Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины \( \small A_1 \) все диагноали многоугольника \( \small A_1A_2. A_
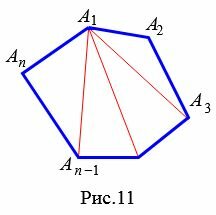 |
Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно \( \small n-3 \). Следовательно, эти диагонали разделяют многоугольник на \( \small n-3+1=n-2 \) треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: \( \small 180°(n-2). \)
где \( \small n \) −количество сторон (вершин) выпуклого многоугольника.
Угол правильного многоугольника
Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:
где \( \small n \) −количество сторон (вершин) правильного многоугольника.
Диагональ
Диагональ (греч. διαγώνιος от δια- «через» и γώνια «угол») в математике имеет геометрический смысл, а также используется при описании квадратных матриц.
Содержание
Многоугольники и многогранники
Для многоугольников, диагональ это отрезок, соединяющий две вершины, не лежащие на одной стороне. Так, четырёхугольник имеет две диагонали, соединяющие противолежащие вершины. У выпуклого многоугольника диагонали проходят внутри него. Многоугольник выпуклый тогда и только тогда, когда его диагонали лежат внутри.
Пусть 



однако, мы посчитали каждую диагональ дважды (по разу для каждого конца) — отсюда,
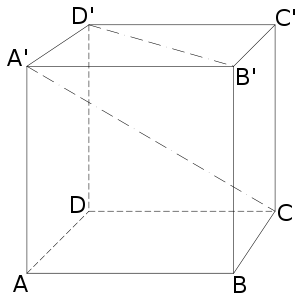
Диагональю многогранника называется отрезок, соединяющий две его вершины, не принадлежащие одной грани. Так, на изображении куба отмечена диагональ 

Аналогично можно определить диагональ и для многогранников в пространствах бо́льших размерностей.
Матрицы
В случае с квадратными матрицами, главная диагональ является диагональной линией элементов, которая проходит с северо-запада на юго-восток. Например, единичная матрица может быть описана, как матрица, имеющая единицы на главной диагонали и нули вне её. Диагональ с юго-запада на северо-восток часто называется побочной диагональю. Наддиагональными элементами называются такие, что лежат выше и правее главной диагонали. Поддиагональными — те, что ниже и левее. Диагональная матрица — такая матрица, у которой все элементы вне главной диагонали равны нулю.
Теория множеств
По аналогии, подмножество декартового произведения X×X произвольного множества X на само себя, состоящее из пар элементов (x, x), называется диагональю множества. Это — единичное отношение, оно играет важную роль в геометрии: например, константные элементы отображения F с X в X могут быть получены сечением F с диагональю множества X.
Внешние ссылки
Полезное
Смотреть что такое «Диагональ» в других словарях:
ДИАГОНАЛЬ — (греч., от dia чрез, и gonia угол). 1) прямая линия, соединяющая в прямолинейной фигуре вершины двух углов, не лежащие на одной прямой. 2) шерстяная материя, тканая волосками в косом направлении очень эластичная. Словарь иностранных слов,… … Словарь иностранных слов русского языка
ДИАГОНАЛЬ — плотная ткань с рельефными рубчиками на лицевой стороне. Выпускается чистошерстяная, полушерстяная и хлопчатобумажная. Чистошерстяная диагональ вырабатывается из тонкой кручёной пряжи. Полушерстяная вырабатывается или из полушерстяной кручёной… … Краткая энциклопедия домашнего хозяйства
диагональ — 1. ДИАГОНАЛЬ, и; ж. [лат. diagonalis] 1. Матем. Отрезок прямой, соединяющий две несмежные вершины многоугольника или две вершины многогранника, не принадлежащие одной грани. Д. квадрата. Д. октаэдра. Разделить квадрат диагональю. Провести д. 2.… … Энциклопедический словарь
ДИАГОНАЛЬ — (от греч. diagonios идущий от угла к углу) отрезок прямой, соединяющий две несмежные вершины многоугольника или две вершины многогранника, не принадлежащие одной грани … Большой Энциклопедический словарь
ДИАГОНАЛЬ — плотная хлопчатобумажная или шерстяная ткань с отчетливо выраженными наклонными рубчиками. Из диагонали шьют воинское обмундирование, куртки и т. д … Большой Энциклопедический словарь
ДИАГОНАЛЬ — ДИАГОНАЛЬ, диагонали, жен. (лат. diagonalis). 1. Прямая линия, соединяющая несмежные вершины многоугольника или многогранника (мат.). || То же спец. о прямой линии, соединяющей противоположные углы прямоугольника и расположенной под острым углом… … Толковый словарь Ушакова
ДИАГОНАЛЬ — ДИАГОНАЛЬ, и, жен. 1. В математике: отрезок прямой линии, соединяющий две вершины многоугольника, не лежащие на одной стороне, или две вершины многогранника, не лежащие на одной грани. 2. Ткань с косыми рубчиками. • По диагонали наискось, не под… … Толковый словарь Ожегова
ДИАГОНАЛЬ — жен. черта, соединяющая два угла, проведенная с угла на угол, в плоском угольнике или в теле; искосина, долонь. Долонь прямоуголыника делит его пополам, на два равные треугольника. | Род французского сукна, с косою низкою. Диагональный искосный,… … Толковый словарь Даля
диагональ — сущ., кол во синонимов: 6 • долонь (6) • искосина (4) • косек (5) • … Словарь синонимов
диагональ — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN diagonal … Справочник технического переводчика
ДИАГОНАЛЬ — отрезок прямой, соединяющий две вершины многоугольника (или многогранника), не лежащие на одной стороне (или на одной грани) … Большая политехническая энциклопедия
Выпуклый многоугольник: определение, элементы, свойства, примеры
Содержание:
А выпуклый многоугольник Это геометрическая фигура, содержащаяся в плоскости, которая характеризуется тем, что все ее диагонали находятся внутри, а ее углы составляют менее 180 °. Среди его свойств можно выделить следующие:
1) Он состоит из n последовательных сегментов, в которых последний из сегментов соединяется с первым. 2) Ни один из сегментов не пересекается таким образом, чтобы ограничить плоскость во внутренней и внешней областях. 3) Каждый угол во внутренней области строго меньше плоского угла.
Элементы многоугольника
Каждый многоугольник состоит из следующих элементов:
Когда у многоугольника все стороны одинаковой длины, мы получаем правильный многоугольник. Все правильные многоугольники выпуклые.
Выпуклые и невыпуклые многоугольники
С другой стороны, число 3 представляет собой многоугольник с четырьмя сторонами, но один из его внутренних углов больше 180 °, поэтому он не удовлетворяет условию выпуклости. То есть это невыпуклый четырехсторонний многоугольник, называемый вогнутым четырехугольником.
Число 4 представляет собой многоугольник с четырьмя отрезками (сторонами), два из которых пересекаются. Четыре внутренних угла меньше 180 °, но поскольку две стороны пересекаются, получается невыпуклый перекрещенный многоугольник (перекрещенный четырехугольник).
Наконец, число 6, у которого также есть пять сторон, имеет все внутренние углы меньше 180º, поэтому это выпуклый многоугольник с пятью сторонами (выпуклый пятиугольник).
Свойства выпуклого многоугольника
1. Непересекающийся многоугольник или простой многоугольник делит содержащую его плоскость на две области. Внутренняя область и внешняя область, многоугольник является границей между двумя областями.
Но если многоугольник дополнительно выпуклый, тогда у нас есть внутренняя область, которая является односвязной, что означает, что, взяв любые две точки из внутренней области, он всегда может быть соединен сегментом, который полностью принадлежит внутренней области.
2- Каждый внутренний угол выпуклого многоугольника меньше плоского угла (180º).
3- Все внутренние точки выпуклого многоугольника всегда принадлежат одной из полуплоскостей, определяемых линией, проходящей через две последовательные вершины.
4- В выпуклом многоугольнике все диагонали полностью содержатся во внутренней многоугольной области.
5- Внутренние точки выпуклого многоугольника полностью принадлежат выпуклому угловому сектору, определяемому каждым внутренним углом.
6. Каждый многоугольник, все вершины которого находятся на окружности, является выпуклым многоугольником, который называется циклическим многоугольником.
7- Каждый циклический многоугольник является выпуклым, но не каждый выпуклый многоугольник является циклическим.
8- Каждый непересекающийся многоугольник (простой многоугольник), все стороны которого равны, является выпуклым и известен как правильный многоугольник.
Диагонали и углы в выпуклых многоугольниках
9- Общее количество N диагоналей выпуклого многоугольника с n сторонами определяется по следующей формуле:
10- Сумма S внутренних углов выпуклого многоугольника с n сторонами определяется следующим соотношением:
Доказательство. Из вершины выводятся n-3 диагонали, определяющие n-2 треугольника. Сумма внутренних углов каждого треугольника составляет 180º. Общая сумма углов n-2 треугольников равна (n-2) * 180º, что совпадает с суммой внутренних углов многоугольника.
Примеры
Пример 1
Пример 2
Определите значение внутренних углов обычного энегона.
Сумма всех внутренних углов 9-стороннего многоугольника равна:
Но существует 9 внутренних углов одинаковой меры α, поэтому должно выполняться равенство:
Отсюда следует, что мера α каждого внутреннего угла правильного ребра равна:
Хеморецепторы: классификация и хемосенсорные системы
8 важнейших биогеохимических циклов (описание)
Выпуклый многоугольник
Что такое выпуклый многоугольник? В чём отличие выпуклого многоугольника от многоугольника, который не является выпуклым?
Выпуклый многоугольник — это многоугольник, лежащий в одной полуплоскости от каждой прямой, содержащей его сторону.
То есть ни одна из прямых, проходящих через две соседние вершины выпуклого многоугольника, не разрезает этот многоугольник на две части.
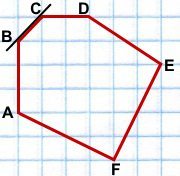
1) ABCDEF — выпуклый шестиугольник, так как он лежит в одной полуплоскости относительно каждой из прямых AB, BC, CD, DE и EF.
2) MNKFEL — не выпуклый шестиугольник,
Он не лежит в одной полуплоскости относительно прямых KF и FE.
Не выпуклый многоугольник можно разбить на конечное число выпуклых многоугольников. Поэтому в курсе геометрии средней школы изучают только выпуклые многоугольники.
Важнейшие виды выпуклых многоугольников
Многоугольники. Выпуклые многоугольники. Четырёхугольники.
Прежде, чем ввести понятие многоугольника, рассмотрим геометрическую фигуру, состоящую из отрезков. Расположим отрезки так, чтобы начало одного отрезка совпадало с концом другого.
Таких отрезков может быть бесконечно много.
Определение. Ломаной называется геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.
Определение. Длиной ломаной называется сумма длин всех её звеньев.
На рисунке длина ломаной равна:
Существует две группы ломаных: замкнутые и незамкнутые.
Определение. Замкнутой называется ломаная, у которой её начало и конец совпадают.
– замкнутая ломаная. У неё точка является и началом и концом.
Замкнутые ломаные также разделяются на две группы:
ломаные без самопересечения (когда несоседние звенья не пересекаются);
ломаные, имеющие самопересечение (когда несоседние звенья пересекаются).
Определение. Многоугольником называется замкнутая ломаная, не имеющая самопересечений.
Определение. Диагональю многоугольника называется отрезок, соединяющий две несоседние вершины.
Любой многоугольник разделяет плоскость на две области: внутреннюю и внешнюю.
Рассмотрим два вида многоугольников.
Визуально видно, что в них есть принципиальная разница. В чём она? Приложите линейку к любой стороне красного многоугольника. Вы заметили, что весь многоугольник находится по одну сторону от линейки. Попробуйте это сделать со всеми остальными сторонами. Многоугольник всё также расположен по одну сторону от линейки.
Теперь перейдём к зелёному многоугольнику и проделаем то же самое: приложим линейку к каждой стороне. Тут вы должны заметить, что существуют две стороны, к которым прикладываем линейку и многоугольник делится на две части. В этом и есть принципиальная разница между этими двумя многоугольниками.
Определение. Выпуклым называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Выпуклый многоугольник можно ещё определить так: это многоугольник, все диагонали которого лежат внутри многоугольника. Если в зелёном многоугольнике провести диагональ через две верхние вершины, то она окажется за пределами самого многоугольника. Поэтому, зелёный многоугольник не является выпуклым. Он называется невыпуклым.
Любой выпуклый многоугольник (кроме треугольника) можно разделить на треугольники его диагоналями. Выясним на примере нескольких многоугольников, сколько можно провести диагоналей из каждой вершины, и сколько получается треугольников.