Что такое дискретные структуры
Что такое дискретность (дискретная математика, сигнал, величины, видеокарты, а так же дискретность в биологии)
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Знать все обо всем попросту невозможно. Человек на протяжении всей жизни стремится познать себя и окружающую его действительность.
Вот и сегодня мы продолжим свой познавательный процесс, поговорим о новом (для многих) термине – « дискретность», и о сферах, где он применяется.
Дискретность – это …
Наш мир непрерывен, мы живем в постоянно меняющемся времени и пространстве. Наша жизнь тоже непрерывна до своего конечного момента. Согласитесь, невозможно сейчас жить, через час не жить, а потом вновь возродиться.
В противопоставлении непрерывности существует дискретность. В переводе с «вечно живого» латинского языка «дискретность» (discretus) обозначает прерывность, разделенность.
Дискре́тность (от лат. discretus — разделённый, прерывистый) — свойство, противопоставляемое непрерывности, прерывистость. Синонимы к слову дискретный: корпускулярный, отдельный, прерывистый, раздельный и т. п.
Например, линия непрерывна (на определенном промежутке), пунктир – прерывистая линия. Поэтому пунктир можно назвать дискретной линией. Проиллюстрирую понятие дискретности:
Дискретность можно толковать следующим образом:
Далее проанализируем особенности применения термина в различных областях.
Дискретная математика
Если коротко и простыми словами, то дискретная математика (ДМ)– это наука, которые изучает математические объекты, принимающие отдельные (дискретные) значения.
ДМ условно подразделяется на пять направлений:
Дискретная величина
Дискретность какой-либо величины подразумевает, что ее значения можно пронумеровать, измерить и посчитать.
Такими величинами оперирует, например, экономика. Различные экономические показатели фиксируют и рассчитывают с определенной периодичностью (например, раз в месяц, квартал, полугодие и т.д.). Таким образом, изменение показателей происходит не непрерывно во времени, а как бы «скачками» через установленные интервалы времени.
Дискретность в информатике
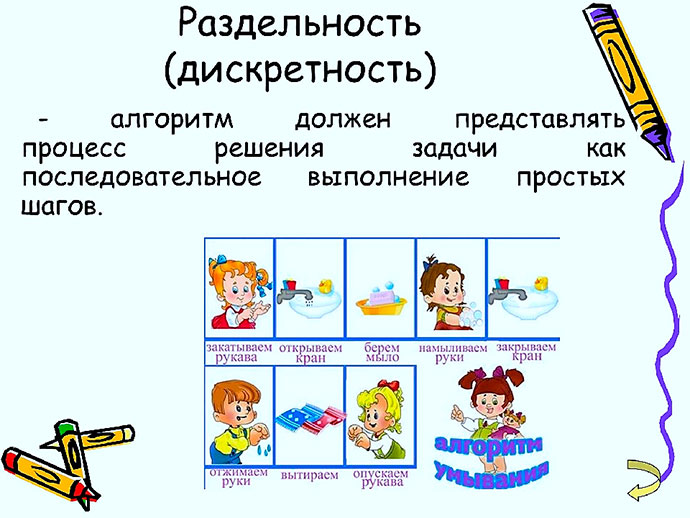
Программирование – это создание программ с использованием различных алгоритмов и языков программирования. Алгоритмы являются дискретными объектами, потому как представляют собой четкое последовательное выполнение ранее разработанных упрощенных шагов-действий (подпрограмм).
Только исполнение шага № 1 дает возможность выполнить шаг № 2 и т.д. Таким образом, этот процесс дискретен.
Как пример – алгоритм умывания (компьютерные программы создаются по тому же принципу):
Дискретная видеокарта
Видеокарта – один из важнейших элементов компьютера, отвечающий за визуализацию информации. Конструкция компа может быть оснащена либо интегрированной (встроенной) видеокартой, либо дискретной. Встроенная размещается в процессоре или на материнской плате, т.е. она неотделима от конкретного компьютера.
Дискретная видеокарта выполнена на отдельной плате, снабжена индивидуальным графическим процессором и памятью. Поэтому она более производительна, чем интегрированная.
Часто в компьютерах применяются видеокарты обоих видов, что позволяет пользователю при необходимости переключаться с одной на другую.
Дискретность в биологии
Все биологические объекты состоят из отдельных (дискретных) «кирпичиков», которые в совокупности образуют единый организм. Например, скелет человека состоит из костей, кости –из костной ткани, она, в свою очередь – из клеток.
Автор статьи: Елена Копейкина
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Благодарю за дискретное изложение материала
Дискретные структуры: матан для айтишников
Посмотришь на любую программу обучения по IT-специальности, и тут же увидишь дисциплину «Дискретная математика» (возможно, под другим названием), обычно для перво- или второкурсников. И её наличие вполне разумно, поскольку дискретная математика и непрерывная математика (представленная на первом курсе институтов с незапамятных времён математическим анализом) — две грани единой Математики, — красивой, могучей науки.
Хотя раньше такого понятия, как «дискретная математика» вовсе не было, это не значит, что не возникало дискретных задач: Абель, Дирихле, Фибоначчи, Эйлер, чьи имена возникают по ходу изучения дискретной математики, — отнюдь не наши современники! Но просто в те времена для выделения самостоятельной ветви математики ещё не сложилось критической массы задач и приёмов, не было видно взаимосвязей между ними. А большое количество плодотворных взаимосвязей между, на первый взгляд, различными понятиями, — то, что математики в своей науке очень ценят.
Ну хорошо, математикам всё математическое интересно. А зачем дискретная математика программисту?
Зачем это айтишнику
Во-первых, многие идеи, которые особенно ярко иллюстрируются на дискретных задачах, неотъемлемы и для информатики. Взять, хотя бы, фундаментальные понятия рекурсии и индукции.
Рекурсия — это, дословно, возврат, обращение к самому себе. Хорошо известные вездесущие числа Фибоначчи проще всего определяются рекурсивно: первые два числа Фибоначчи равны единице, а каждое следующее число равно сумме двух своих предшественников: 1,1,2,3,5,8,… Таким образом, для вычисления очередного числа мы обращаемся к уже рассчитанным числам такого же вида. Трудно представить, как можно изучить функциональное программирование, да и многое из других областей информатики, не освоившись хорошо с рекурсией. Очень близкий процесс к рекурсии — это индукция, способ доказательства математических утверждений, при котором в доказательстве сложных случаев мы опираемся на более простые. Параллели с рекурсией очевидны, и действительно, обычное дело, когда индуктивное доказательство существования какого-то объекта можно переформулировать в описание рекурсивного способа построения этого объекта.
Раз речь зашла о таких фундаментальных вещах, как индукция и рекурсия, не могу не сказать, что многие приёмы, которые очень хорошо видны на примерах из дискретной математики, эффективны в математике в целом. Это не только индукция, но и принцип Дирихле, принцип выбора по среднему значению и другие.
Следующий элемент, без которого информатику нельзя представить — это графы. Простейшие алгоритмы на графах обязательно входят в любой, даже самый вводный, курс по алгоритмам. Скажем, с понятием гамильтонова цикла связана одна из классических задач информатики, задача коммивояжёра.
Ещё одно архиважное умение — считать точно и оценивать приблизительно количества. Например, как вычислить количество раз, которые выполняется операция сравнения в цикле:
Или вот ещё пример. Нужно из списка из 100 товаров выбрать 20, так, чтобы их суммарная стоимость была ровно 2000 рублей («без сдачи»). Это вариант классической задачи о рюкзаке. Допустим, ваш коллега, подумав ночь, предложил решать задачу перебором: перебрать всевозможные наборы из двадцати товаров, и, как только в ходе перебора возникнет нужный набор, выдать его в качестве ответа. Между прочим, характеристика «переборный» далеко не всегда ставит клеймо на алгоритме. Всё зависит от размера входных данных. Так вот, как прикинуть, удастся ли за разумное время решить перебором эту задачу выбора 20 объектов из 100?
Наконец, для современного «дизайнера алгоритмов» обязателен к пониманию и вероятностный метод. Это общий метод, позволяющей решать многие задачи в современной комбинаторике. Очень часто наилучшие решения задач, известные на сегодняшний день, получены именно этим методом. Для практика же овладение этим методом полезно постольку, поскольку вероятностные алгоритмы прочно заняли место в современной информатике. И при анализе работы таких алгоритмов очень помогает интуиция, развитая в ходе изучения вероятностного метода.
Онлайн-курс «Дискретные структуры»
С верой в то, что перечисленные понятия из дискретной математики действительно не помешают любому программисту, а, скорее, помешает их незнание, я читаю соответствующий курс на факультете ФИВТ МФТИ. А недавно у меня появилась возможность сделать онлайн-курс, чем я с радостью воспользовался. Записаться на него можно по ссылке. Главное, чего я пожелаю всем записавшимся: не побоявшись трудностей, пройти курс до самого конца, и получить заслуженное звание Дипломированного Дискретчика. В общем, чтобы MOOC прошёл без мук и обогатил знаниями! Да и собственная корысть у меня тут тоже есть: чем больше онлайн-учеников у меня будет, тем большему я смогу научиться, читая обсуждения и наблюдая статистику решения задач. Ведь учиться учить тоже никогда не поздно!
Какие знания потребуются
Для прохождения первых двух модулей потребуются только школьные знания. Третий модуль потребует знание основ математического анализа на уровне «что такое предел» и «какая из функций x 20 или 2 x растёт быстрее (чему равны производные функций)». Для последних трёх модулей понадобится представление о том, что такое вероятность, условная вероятность, математическое ожидание, дисперсия. Также хорошо бы знать, что такое базис и размерность линейного пространства. Если с вероятностью и линейной алгеброй вы не знакомы, можно записаться заодно на эти вводные курсы. Тогда как раз, к моменту, когда нам потребуются эти знания, они у вас будут.
Post scriptum
Меня можно было бы упрекнуть в конфликте интересов, всё-таки я математик, и, естественно, хочу приобщить к своей секте как можно больше завсегдатаев Хабра. В своё оправдание могу сослаться на этот ответ на Quora. Под большей частью тем, перечисленных в этом ответе, я готов лично подписаться, в онлайн-курс многие из них вошли. Ещё сошлюсь на подборку мнений яндексоидов.
Дискретные структуры (DS)
Дискретные структуры являются фундаментальной основой информатики. Под фундаментальными мы имеем в виду то, что сравнительно небольшое число ученых будут работать непосредственно в этой дисциплине, однако во многих других областях компьютерных наук требуется умение работать с понятиями дискретных структур. Дискретные структуры включают в себя важный материал из таких областей, как теория множеств, логика, теория графов и комбинаторика.
Сведения из теории дискретных структур широко используются не только в структурах данных и алгоритмах, но и во всех остальных разделах информатики.
Сведения из теории дискретных структур широко используются не только в структурах данных и алгоритмах, но и во всех остальных разделах информатики. Например, при проверке формальных спецификаций, верификации, а также в криптографии необходимо уметь создавать и понимать формальные доказательства. Понятия теории графов используются в сетях, операционных системах и компиляторах. Теория множеств находит применение в программной инженерии и базах данных.
По мере развития информатики, все более и более сложные методы анализа оказывают влияние на практические проблемы для того, чтобы освоить вычислительные средства будущего, сегодняшним студентам потребуется твердое знание дискретных структур.
В заключение заметим, что существуют области знания, границы которых очень трудно определить, и теория дискретных структур, безусловно, является одним из примеров таких областёй. Здесь собраны математические основы, которые должны преподаваться при обучении информатики, и которые достаточно хорошо известны, чтобы преподаватели информатики могли читать их с большой степенью подробности. Однако, решение о том, где проходит граница между темами, освещаемыми в дискретных структурах, алгоритмах или теории сложности, с одной стороны, и темами, оставленными в виде вспомогательных разделов математики, с другой стороны, неизбежно носит несколько волюнтаристский характер.
Следует отметить, что есть важные темы из этих двух областей, которые в некоторых школах будут включать в курсы с названиями «дискретные структуры» и «Дискретная математика», некоторым понадобится один курс, остальным два. В апреле 2007 года SIGCSE комитет выступил с подробным докладом по трем моделям односеместрового курса по дискретной математике, отвечающим критериям, сформулированным в CS2001. Эти модели по-прежнему применимы с учетом скорректированного в CS2008 объема знаний.
DS. Дискретные структуры (43 основных часов)
DS1/Функции Отношения Множества [основной]
DS2/Основы логики [основной]
DS3/Методы доказательства [основной]
DS4/Основы вычислений [основной]
DS5/Графы и деревья [основной]
DS6/Дискретная вероятность [основной]
DS/Функции Отношения Можества [основной]
Минимальное время, отводимое на модуль: 6 часов
· Функции (сюръекции, инъекции, обратные функции, композиция)
· Отношения (рефлексивность, симметричность, транзитивность, эквивалентность)
· Множества (диаграммы Венна, дополнения, декартовы произведения, степенные множества)
· Мощность и счетность
1. Объяснять с примерами основные понятия функций, отношений и множеств.
2. Выполнять операций, связанные с множествами, функциями и отношениями.
3. Связывать практические примеры с подходящими моделями множеств, функций и отношений, а также дать в
этом контексте интерпретацию соответствующих операций.
Минимальное время: 10 часов
- Логика высказываний Логические связки Таблицы истинности Нормальные формы (конъюнктивные и дизъюнктивные) Общезначимость (тавтология) Логика предикатов Кванторы всеобщности и существования Правила modus ponens и modus tollens Ограничения логики предикатов
1. Обучить применению формальных методов символической логики высказываний и логики предикатов.
2. Показать использование формальных средств символической логики для моделирования алгоритмов и реаль-
ных жизненных ситуаций.
3. Использовать формальные логические доказательства и логическое рассуждение для решения задач, напри-
4. Описать применимость и ограничения логики предикатов.
Минимальное время: 12 часов
- Понятия импликации, обращения, противопоставления, контрапозиции, отрицания и противоречия Структура формальных доказательств Прямые доказательства Доказательство через контрпример Доказательство через контрапозицию Доказательство через противоречие Математическая индукция Сильная индукция Рекурсивные математические определения Вполне упорядоченные множества
1. Обрисовать основную структуру и дать примеры каждого метода доказательств, описанных выше.
2. Обсудить, какой вид доказательства лучше подходит для данной задачи.
3. Связать идеи математической индукции с понятием рекурсии и рекурсивно определенных структур.
4. Указать различия между математической и сильной индукцией и дать примеры адекватного использования
каждого из этих методов.
Минимальное время: 5 часов
- Основы вычислений: Правила суммы и произведения Принцип включения-выключения Арифметические и геометрические прогрессии Числа Фибоначчи Принцип Дирихле Перестановки и сочетания Основные определения Тождество Паскаля Биномиальная теорема Решение рекуррентных соотношений Общие примеры Основная теорема рекуррентных соотношений
1. Вычислять перестановки и сочетания множества, а также интерпретировать их значения в контек-
сте конкретного приложения.
2. Формулировать основную теорему рекуррентных соотношений.
3. Решать типичные рекуррентные соотношения.
4. Анализировать задачу построения рекуррентных уравнений или выявлять связанные с ней вычислительные вопросы.
Минимальное время: 4 часа
- Деревья Неориентированные графы Ориентированные графы Остовные деревья/леса Стратегии обхода графов
1. Иллюстрировать на примерах основные понятия теории графов, а также их свойства и специальные случаи использования.
2. Демонстрировать различные методы обхода деревьев и графов.
3. Использовать деревья и графы при моделировании задач информатики.
4. Показывать связь графов и деревьев со структурами данных, алгоритмами и вычислениями.
Минимальное время: 6 часов
- Конечное вероятностное пространство, вероятностная мера, события Условная вероятность, независимость событий, теорема Байеса Целочисленные случайные величины, математическое ожидание Закон больших чисел
1. Вычислять вероятности событий и математического ожидания случайных величин для элементарных задач, таких как игра в рулетку.
2. Различать независимые и зависимые события.
3. Применять биномиальную теорему для независимых событий и теорему Байеса для зависимых событий.
4. Применять вероятностные методы к решению таких задач, как метод Монте-Карло, анализ среднего случая алгоритмов и хеширование.
1. Санкт-Петербургский государственный университет. Рекомендации по преподаванию информатики в университетах. С.-Петербург, 2002
2. Computer Science 2008 (CS2008). Association for Computing Machinery and Computer Society of IEEE.
Дискретность в физике и математике. Лекция. Катющи
Дискретный простыми словами – прерывный, разделенный, зернистый, отдельный
— свойство, противопоставляемое непрерывности.
Каждый способен отличить прерывное от непрерывного.
Но если смотреть глубже, то дискретность можно разделить на наружную и внутреннюю.
И гранат например имеет внутреннюю дискретность (состоит из отдельных зёрен), а так же сам может быть рассмотрен как отдельное зерно. На своей поверхности гранат прервался и дальше уже не гранат.
И когда мы например, говорим: «Маша мыла раму», мы должны четко понимать, что Маша так же имеет наружную дискретность – то есть: имеет самостоятельный внешний контур – является самостоятельным объектом.
Так же Маша имеет внутреннюю дискретность – состоит из клеточек. И швабра у Маши так же имеет и внешнюю и внутреннюю дискретность.
И здесь тоже все просто.
Но есть определенные подробности и у многих людей с недискретным, с непрерывным возникают трудности. Попробуем пояснить почему.
Представьте человека, который вырос в глухой степи и по случайному стечению обстоятельств ему никто не рассказал про экскаватор.
И единственное что у него в голове срабатывает:
— Это какие же здесь суслики водятся, что они такую яму вырыли.
И есть вполне конкретные типы задач, который в определенном смысле навязывает воображаемого кимберлитового суслика.
В этом списке и задача на дискретность.
И опять же накладываются представления, что все что нас окружает – состоит из атомов, имеет корпускулярную сущность.
Например, стена её можно пощупать и мы воспринимаем её относительную непрерывность, но жизненный опыт показывает, что у этой непрерывности должен быть внешний край, конец, а значит и стена какая бы длинная она не была в конечном итоге дискретна ( и сама по себе это тоже отдельный элемент). То есть непрерывность (на примере стены) конечна – имеет место наружная дискретность, наружная прерывность.
Следующая позиция №4
Непрерывность материальная, но не вещественная.
Что у нас в природе вообще есть материальное, но не вещественное?
И что материальное может быть фундаментально непрерывным?
И применительно к полю ряд людей вновь, сами не понимая почему – готовы сделать выбор в пользу дискретного решения.
Человеку просто кажется, что и в этом случае неизменно должны быть какие-то дискретные штуки.
В этих случаях помочь не всегда возможно, но на всякий случай сообщаем.
Справочно:
Кимберлитовые суслики не внесены в красную книгу
не находятся под защитой здравого смысла и их можно смело утилизировать.
Для остальных просто напомним, что поле не имеет массы, не имеет вещественности. У поля нет той самой штуки которая может обеспечить внутреннюю дискретность.
Так же у поля нет наружной дискретности. Потому что поле не ограничивается с расстоянием.
И это мы можем наглядно продемонстрировать через график распределения поля в пространстве.
Если мы расположим в пространстве некий единичный источник воздействия, и окружим его некой сферой, то с расширением этой сферы её площадь будет увеличиваться и следовательно будет уменьшаться доля воздействия выпадающая на единицу площади этой сферы.
Формульно это выражается через площадь поверхности сферы
А поскольку речь идет о рассеивании единичного воздействия на поверхность сферы то мы имеем единицу деленную на площадь поверхности сферы, то есть
данное распределение воздействия соответствует приведенному графику.
И в связи с эти мы должны понимать, что даже поле от маленького комаринного магнитика распространяется бесконечно далеко и не имеет внешних границ.
При этом по мере удаления потенциал поля стремится к нулю но никогда через этот нуль не переходит.
Итого применительно к физике мы можем выделить 4 вида дискретных и недискретных состояний.
позиция №1
— Наружная дискретность. Присуща материи разделенной на отдельные фрагменты. Материя имеющая внешние границы.
Позиция № 2
— внутренняя дискретность в рамках некой непрерывности
— присуща материи имеющей общую протяженную вещественную непрерывность, и внутреннее дискретное строение в форме отдельных элементов.
В эту категорию попадают все объекты состоящие из вещества, которые внешне воспринимаются как непрерывные, но по своей структуре состоят из более мелких частей.
Позиция № 3
непрерывность нематериальная (присущая пространству) не имеющая внутренней структуры (внутренней дискретности).
позиция №4
Непрерывность материальная невещественная (присущая физическому полю).
Данные четыре позиции желательно твёрдо запомнить. Это облегчит понимание физики в целом.
Собственно всё.
С вами был Виктор Катющик.
Подписывайтесь на видеоканал.
Следите за нашими публикациями.
Основы дискретной математики
Привет, хабр. В преддверии старта базового курса «Математика для Data Science» делимся с вами переводом еще одного полезного материала.
Об этой статье
Эта статья содержит лишь малую часть информации по заявленной теме. Рассматривайте ее как вводный курс перед началом всестороннего изучения предмета. Надеюсь, вы найдете в ней полезную информацию. Знание дискретной математики помогает описывать объекты и задачи в информатике, особенно когда дело касается алгоритмов, языков программирования, баз данных и криптографии. В дальнейшем я планирую подробнее раскрыть темы, затронутые в этой статье. Приятного чтения!
ЧТО ТАКОЕ ДИСКРЕТНАЯ МАТЕМАТИКА?
Это область математики, изучающая объекты, которые могут принимать только уникальные отдельные значения.
Мы рассмотрим пять основных разделов в следующем порядке.
ЛОГИКА
Что такое логика?
Это наука о корректных рассуждениях. Мы будем использовать приемы идеализации и формализации. Неформальная логика изучает использование аргументов в естественном языке.
Формальная логика анализирует выводы с чисто формальным содержанием. Примерами формальной логики являются символическая логика и силлогистическая логика (о которой писал Аристотель).
Начнем с азов. Рассмотрим следующее высказывание на естественном языке:
«Если я голоден, я ем».
Пусть «голоден» будет посылкой A, а «ем» — следствием B. Попробуем формализовать:
A => B (то есть из A следует B)
NB. Посылка и следствие являются суждениями.
Логические выражения
Для нас важна форма, а НЕ содержание. Значение будет истинным, если оно соответствует форме.
Например, 10 4 — ИСТИНА.
Логические операции
Суждение P — это утверждение, которое может быть как истинным, так и ложным.
Обозначим истинное значение P единицей (1), а ложное значение P нулем (0).
Существует другое суждение; обозначим истинное значение Q единицей (1), а ложное значение Q нулем (0).
Рассмотрим логические операции с суждениями, значение которых истинно. Они могут сами образовывать истинные значения путем выполнения соответствующих операций над истинными значениями.