Что такое длина сднф
Совершенная нормальная форма — дизъюнктивная и конъюнктивная, правило построения
Что такое СДНФ
Нормальная форма логической формулы характеризуется тем, что для нее не свойственны эквивалентность, отрицание формул неэлементарного типа и знаки импликации.
Существует две формы нормального типа: КНФ (конъюнктивная нормальная форма) и ДНФ (дизъюнктивная нормальная форма).
СДНФ — совершенная дизъюнктивная нормальная форма формулы. СДНФ — способ написания функции алгебры логики в качестве логического выражения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
СДНФ формулы — это равнозначная ей формула, которая представляет собой дизъюнкцию элементарных конъюнкций, при которых функция достигает показателя «1».
ДНФ выглядит следующим образом:
СДНФ обладает некоторыми определенными свойствами:
К СДНФ возможно привести любую формулу алгебры логики. Исключение составляет только тождественно ложная формула. СДНФ можно получить как используя таблицы истинности, так и через равносильные преобразования.
При построении таблицы истинности важно помнить, что логические переменные со значением «0» необходимо брать с отрицанием.
Что такое СКНФ
СКНФ — совершенная конъюнктивная нормальная форма. Формулу можно назвать таковой, когда она — конъюнкция неповторяющихся элементарных дизъюнкций.
Формула должна соответствовать нескольким условиям, чтобы называться СКНФ:
Правила построения по таблице истинности
Дизъюнктивная форма
Если функция равна 1, то для всех наборов переменных, при которых это происходит, записывается произведение. Однако переменные, которые имеют значение 0, берутся с отрицанием.
Конъюнктивная форма
Когда функция равна 0, то для всех наборов переменных, при которых это происходит, записывается сумма. Однако переменные, которые имеют значение 1, берутся с отрицанием.
Алгоритм приведения к СДНФ и СКНФ
Рассмотрим логическую функцию в виде таблицы истинности.
Алгоритм построения СДНФ по таблице истинности выглядит следующим образом:
Построим совершенную ДНФ:
И как результат получим следующую СДНФ:
Алгоритм построения СКНФ по таблице истинности выглядит следующим образом:
Построим совершенную КНФ:
И как результат получим следующую СКНФ:
Рассмотрев алгоритмы построения СДНФ и СКНФ ясно, что в случае подавляющей части наборов значений переменных функция равна 0, то значительно легче построить и СДНФ для получения ее формулы, а в обратном случае — СКНФ.
Доказательство эквивалентности
Доказать эквивалентность формул можно двумя способами.
Далее следуют примеры с некоторыми эквивалентными преобразованием в булевой алгебре и новыми эквивалентностями, которые возможно получить с их помощью.
Поглощение
Склеивание
Обобщенное склеивание
\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\)
\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\;\vee\;xyz\;\vee\;xy\overline z\;=\;xz\;\vee\;y\overline z\)
Расщепление
\(x\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;xy\;\vee\;\overline xy\;=\;x\;\cdot\;l\;\;\vee\;y\;\cdot\;l\;=\;x\;\vee\;y\)
Примеры с решением
Задача №1
Через применение закона де Моргана и правила \( x\;\rightarrow\;y\;=\;\overline x\;\vee\;y\) упростим выражения:
\(F\;=\;((((A\;\rightarrow\;B)\;\rightarrow\;\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;(((\overline A\;\vee\;B)\;\rightarrow\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\overline C\;)\;=\)
\(=\;((((\overline A\;\vee\;B)\;\rightarrow\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;((\overline<((\overline A\;\vee\;B)>\;\vee\;\overline A)\;\rightarrow\overline B)\;\rightarrow\overline C)\;=\)
\(=(((\overline A\;\vee\;B)\;\vee\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\;\overline C)\;=((\overline<(\overline<(\overline A\vee B)>\;\vee\;\overline A\;)>\;\vee\;\overline B)\;\rightarrow\;\overline C)\;=\)
\(=\;((\overline<(\overline A\;\vee\;B)>\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge B)\;\vee\;\overline C\;=\)
\(=((A\overline B\;\vee\;\overline A)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\)
\(=\;((A\overline B\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(A\overline BB\;\vee\;\overline AB)\;\vee\;\overline C\;=\;(0\;\vee\;\overline AB)\;\vee\;\overline C\;=\;\overline AB\;\vee\;\overline C\)
Далее приведем выражение к КНФ:
\(F\;=\;\overline AB\;\vee\;\overline C\;\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\)
Далее приведем выражение к СКНФ:
\(F\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\;=\;(\overline A\;\vee\:\overline C\;\vee\;B\overline B)\;\wedge\;(A\overline A\;\vee\;B\;v\;\overline C)\;=\)
\(=\;(\overline A\;\vee\;\overline C\;\vee\;B)\;\wedge\;(A\;\vee\;B\;\vee\;\overline C)\;\wedge\;(\overline A\;\vee\;\overline C\;\vee\;\overline B)\;\wedge\;(\overline A\;\vee\;B\;\;\overline C)\)
Задача №2
Используя эквивалентные преобразования, постройте ДНФ функции \(f(\widetilde x^n)\)
\(f(\widetilde x^3) = (\overline
\(f(\widetilde x^3) = (\overline
\(=(\overline
Построение таблицы истинности. СДНФ. СКНФ. Полином Жегалкина.
Онлайн калькулятор позволяет быстро строить таблицу истинности для произвольной булевой функции или её вектора, рассчитывать совершенную дизъюнктивную и совершенную конъюнктивную нормальные формы, находить представление функции в виде полинома Жегалкина, строить карту Карно и классифицировать функцию по классам Поста.
Калькулятор таблицы истинности, СКНФ, СДНФ, полинома Жегалкина
введите функцию или её вектор
Построено таблиц, форм:
Как пользоваться калькулятором
Видеоинструкция к калькулятору
Используемые символы
Для смены порядка выполнения операций используются круглые скобки ().
Обозначения логических операций
Что умеет калькулятор
Что такое булева функция
Что такое таблица истинности?
Довольно часто встречается вариант таблицы, в которой число столбцов равно n + число используемых логических операций. В такой таблице также первые n столбцов заполнены наборами аргументов, а оставшиеся столбцы заполняются значениями подфункций, входящих в запись функции, что позволяет упростить расчёт конечного значения функции за счёт уже промежуточных вычислений.
Логические операции
Логическая операция — операция над высказываниями, позволяющая составлять новые высказывания путём соединения более простых. В качестве основных операций обычно называют конъюнкцию (∧ или &), дизъюнкцию (∨ или |), импликацию (→), отрицание (¬), эквивалентность (=), исключающее ИЛИ (⊕).
Таблица истинности логических операций
| a | b | a ∧ b | a ∨ b | ¬a | ¬b | a → b | a = b | a ⊕ b |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
Как задать логическую функцию
Есть множество способов задать булеву функцию:
Рассмотрим некоторые из них:
Чтобы задать функцию в виде формулы, необходимо записать математическое выражение, состоящее из аргументов функции и логических операций. Например, можно задать такую функцию: a∧b ∨ b∧c ∨ a∧c
Способы представления булевой функции
С помощью формул можно получать огромное количество разнообразных функций, причём с помощью разных формул можно получить одну и ту же функцию. Иногда бывает весьма полезно узнать, как построить ту или иную функцию, используя лишь небольшой набор заданных операций или используя как можно меньше произвольных операций. Рассмотрим основные способы задания булевых функций:
Совершенная дизъюнктивная нормальная форма (ДНФ)
Простая конъюнкция — это конъюнкция некоторого конечного набора переменных, или их отрицаний, причём каждая переменная встречается не более одного раза.
Дизъюнктивная нормальная форма (ДНФ) — это дизъюнкция простых конъюнкций.
Совершенная дизъюнктивная нормальная форма (СДНФ) — ДНФ относительно некоторого заданного конечного набора переменных, в каждую конъюнкцию которой входят все переменные данного набора.
Например, ДНФ является функция ¬a bc ∨ ¬a ¬b c ∨ ac, но не является СДНФ, так как в последней конъюнкции отсутствует переменная b.
Совершенная конъюнктивная нормальная форма (КНФ)
Простая дизъюнкция — это дизъюнкция одной или нескольких переменных, или их отрицаний, причём каждая переменная входит в неё не более одного раза.
Конъюнктивная нормальная форма (КНФ) — это конъюнкция простых дизъюнкций.
Совершенная конъюнктивная нормальная форма (СКНФ) — КНФ относительно некоторого заданного конечного набора переменных, в каждую дизъюнкцию которой входят все переменные данного набора.
Например, КНФ является функция (a ∨ b) ∧ (a ∨ b ∨ c), но не является СДНФ, так как в первой дизъюнкции отсутствует переменная с.
Алгебраическая нормальная форма (АНФ, полином Жегалкина)
Алгебраическая нормальная форма, полином Жегалкина — это форма представления логической функции в виде полинома с коэффициентами вида 0 и 1, в котором в качестве произведения используется операция конъюнкции, а в качестве сложения — исключающее ИЛИ.
Примеры полиномов Жегалкина: 1, a, a⊕b, ab⊕a⊕b⊕1
Алгоритм построения СДНФ для булевой функции
Алгоритм построения СКНФ для булевой функции
Алгоритм построения полинома Жегалкина булевой функции
Есть несколько методов построения полинома Жегалкина, в данной статье рассмотрим наиболее удобный и простой из всех.
Примеры построения различных представлений логических функций
Построим совершенные дизъюнктивную и дизъюнктивную нормальные формы, а также полином Жегалкина для функции трёх переменных F = ¬a b∨ ¬b c∨ca
1. Построим таблицу истинности для функции
| a | b | c | ¬a | ¬a ∧b | ¬b | ¬b ∧c | ¬a ∧b∨ ¬b ∧c | c∧a | ¬a ∧b∨ ¬b ∧c∨c∧a |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
Построение совершенной дизъюнктивной нормальной формы:
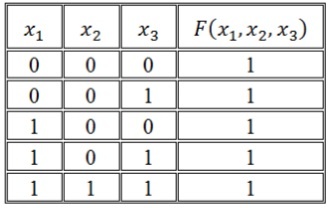
Найдём наборы, на которых функция принимает истинное значение: < 0, 0, 1 > < 0, 1, 0 > < 0, 1, 1 > < 1, 0, 1 >
В соответствие найденным наборам поставим элементарные конъюнкции по всем переменным, причём если переменная в наборе принимает значение 0, то она будет записана с отрицанием:
Объединим конъюнкции с помощью дизъюнкции и получим совершенную дизъюнктивную нормальную форму:
Построение совершенной конъюнктивной нормальной формы:
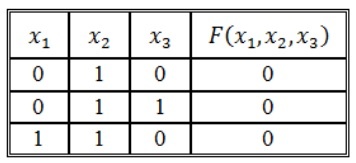
Найдём наборы, на которых функция принимает ложное значение: < 0, 0, 0 > < 1, 0, 0 >
В соответствие найденным наборам поставим элементарные дизъюнкции по всем переменным, причём если переменная в наборе принимает значение 1, то она будет записана с отрицанием:
Объединим дизъюнкции с помощью конъюнкции и получим совершенную конъюнктивную нормальную форму:
Построение полинома Жегалкина:
Добавим новый столбец к таблице истинности и запишем в 1, 3, 5 и 7 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 2, 4, 6 и 8 сложим по модулю два со значениями из соответственно 1, 3, 5 и 7 строк:
| a | b | c | F | 1 | |
| 0 | 0 | 0 | 0 | → | 0 |
| 0 | 0 | 1 | 1 | ⊕ 0 | 1 |
| 0 | 1 | 0 | 1 | → | 1 |
| 0 | 1 | 1 | 1 | ⊕ 1 | 0 |
| 1 | 0 | 0 | 0 | → | 0 |
| 1 | 0 | 1 | 1 | ⊕ 0 | 1 |
| 1 | 1 | 0 | 0 | → | 0 |
| 1 | 1 | 1 | 1 | ⊕ 0 | 1 |
Добавим новый столбец к таблице истинности и запишем в 1 и 2, 5 и 6 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 3 и 4, 7 и 8 сложим по модулю два со значениями из соответственно 1 и 2, 5 и 6 строк:
| a | b | c | F | 1 | 2 | |
| 0 | 0 | 0 | 0 | 0 | → | 0 |
| 0 | 0 | 1 | 1 | 1 | → | 1 |
| 0 | 1 | 0 | 1 | 1 | ⊕ 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | ⊕ 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | → | 0 |
| 1 | 0 | 1 | 1 | 1 | → | 1 |
| 1 | 1 | 0 | 0 | 0 | ⊕ 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | ⊕ 1 | 0 |
Добавим новый столбец к таблице истинности и запишем в 1 2, 3 и 4 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 5, 6, 7 и 8 сложим по модулю два со значениями из соответственно 1, 2, 3 и 4 строк:
| a | b | c | F | 1 | 2 | 3 | |
| 0 | 0 | 0 | 0 | 0 | 0 | → | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | → | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | → | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | → | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | ⊕ 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 | ⊕ 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | ⊕ 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | ⊕ 1 | 1 |
Окончательно получим такую таблицу:
| a | b | c | F | 1 | 2 | 3 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 |
Выпишем наборы, на которых получившийся вектор принимает единичное значение и запишем вместо единиц в наборах имена переменных, соответствующие набору (для нулевого набора следует записать единицу):
Объединяя полученные конъюнкции с помощью операции исключающего или, получим полином Жегалкина: c⊕b⊕bc⊕ab⊕abc
Programforyou — это сообщество, в котором Вы можете подтянуть свои знания по программированию, узнать, как эффективно решать те или иные задачи, а также воспользоваться нашими онлайн сервисами.
СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице
СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице
СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице
Простой конъюнкцией или конъюнктом называется конъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная встречается не более одного раза.
ДНФ — нормальная форма, в которой булева функция имеет вид дизъюнкции нескольких простых конъюнктов.
СДНФ — это такая ДНФ, которая удовлетворяет условиям:
Для любой булевой функции выполняется следующее соотношение, называемое разложением Шеннона.
Алгоритм построения СДНФ по таблице истинности
Пример построения СДНФ для медианы
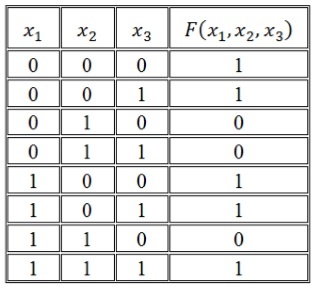
В таблице истинности отмечаем те наборы переменных, на которых значение функции равно 1.
| x | y | z | $\langle x,y,z \rangle$ |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть 1, то в конъюнкцию включаем саму переменную, иначе ее отрицание.
Примеры СДНФ для некоторых функций
а > в ней нет одинаковых дизъюнктивных элементов;
б > ни одна элементарная конъюнкция не содержит двух одинаковых высказываний;
в > ни какая элементарная конъюнкция не содержит высказывание вместе с ее отрицанием;
Условие а > – г > являются необходимыми и достаточными для того, чтобы ДНФ стала СДНФ. В свою очередь эти условия дают возможность составить алгоритм получения СДНФ из ДНФ:
2) если в полученном выражении окажутся одинаковые элементарные конъюнкции, то лишние опускаются;
3) если в некоторых элементарных конъюнкциях окажутся одинаковые высказывания, то лишние опускаются;
4) удаляем элементарные конъюнкции, в которых содержатся высказывания вместе с их отрицанием.
Если все элементарные конъюнкции окажутся таковыми, т.е. вся формула будет ложной, то она не будет иметь СДНФ.
Если все элементарные конъюнкции окажутся таковыми, т.е. вся формула будет ложной, то она не будет иметь СДНФ.
Все элементарные конъюнкции в такой ДНФ попарно различны.
Совершенная дизъюнктивная нормальная форма представляет собой формулу, построенную по строго определенным правилам с точностью до порядка следования элементарных конъюнкций < дизъюнктивных членов >в ней.
Она является примером однозначного представления булевой функции в виде формульной < алгебраической >записи.
Алгоритм построения СДНФ по таблице истинности:
Далее:
Свойства двойного интеграла
Теорема об алгоритме распознавания полноты
Критерий полноты
Равносильные формулы алгебры высказываний
Определение криволинейного интеграла второго рода
Механические приложения двойного интеграла
Вычисление площади поверхности
Класс M. Теорема о замкнутости класса M
Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина
Вычисление объёмов
Теорема о полныx системаx в Pk
Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных
Полином Жегалкина. Пример.
Построение таблицы истинности. СДНФ. СКНФ. Полином Жегалкина.
Онлайн калькулятор позволяет быстро строить таблицу истинности для произвольной булевой функции или её вектора, рассчитывать совершенную дизъюнктивную и совершенную конъюнктивную нормальные формы, находить представление функции в виде полинома Жегалкина, строить карту Карно и классифицировать функцию по классам Поста.
Калькулятор таблицы истинности, СКНФ, СДНФ, полинома Жегалкина
введите функцию или её вектор
Построено таблиц, форм:
Как пользоваться калькулятором
Видеоинструкция к калькулятору
Используемые символы
Для смены порядка выполнения операций используются круглые скобки ().
Обозначения логических операций
Что умеет калькулятор
Что такое булева функция
Что такое таблица истинности?
Довольно часто встречается вариант таблицы, в которой число столбцов равно n + число используемых логических операций. В такой таблице также первые n столбцов заполнены наборами аргументов, а оставшиеся столбцы заполняются значениями подфункций, входящих в запись функции, что позволяет упростить расчёт конечного значения функции за счёт уже промежуточных вычислений.
Логические операции
Логическая операция — операция над высказываниями, позволяющая составлять новые высказывания путём соединения более простых. В качестве основных операций обычно называют конъюнкцию (∧ или &), дизъюнкцию (∨ или |), импликацию (→), отрицание (¬), эквивалентность (=), исключающее ИЛИ (⊕).
Таблица истинности логических операций
| a | b | a ∧ b | a ∨ b | ¬a | ¬b | a → b | a = b | a ⊕ b |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
Как задать логическую функцию
Есть множество способов задать булеву функцию:
Рассмотрим некоторые из них:
Чтобы задать функцию в виде формулы, необходимо записать математическое выражение, состоящее из аргументов функции и логических операций. Например, можно задать такую функцию: a∧b ∨ b∧c ∨ a∧c
Способы представления булевой функции
С помощью формул можно получать огромное количество разнообразных функций, причём с помощью разных формул можно получить одну и ту же функцию. Иногда бывает весьма полезно узнать, как построить ту или иную функцию, используя лишь небольшой набор заданных операций или используя как можно меньше произвольных операций. Рассмотрим основные способы задания булевых функций:
Совершенная дизъюнктивная нормальная форма (ДНФ)
Простая конъюнкция — это конъюнкция некоторого конечного набора переменных, или их отрицаний, причём каждая переменная встречается не более одного раза.
Дизъюнктивная нормальная форма (ДНФ) — это дизъюнкция простых конъюнкций.
Совершенная дизъюнктивная нормальная форма (СДНФ) — ДНФ относительно некоторого заданного конечного набора переменных, в каждую конъюнкцию которой входят все переменные данного набора.
Например, ДНФ является функция ¬a bc ∨ ¬a ¬b c ∨ ac, но не является СДНФ, так как в последней конъюнкции отсутствует переменная b.
Совершенная конъюнктивная нормальная форма (КНФ)
Простая дизъюнкция — это дизъюнкция одной или нескольких переменных, или их отрицаний, причём каждая переменная входит в неё не более одного раза.
Конъюнктивная нормальная форма (КНФ) — это конъюнкция простых дизъюнкций.
Совершенная конъюнктивная нормальная форма (СКНФ) — КНФ относительно некоторого заданного конечного набора переменных, в каждую дизъюнкцию которой входят все переменные данного набора.
Например, КНФ является функция (a ∨ b) ∧ (a ∨ b ∨ c), но не является СДНФ, так как в первой дизъюнкции отсутствует переменная с.
Алгебраическая нормальная форма (АНФ, полином Жегалкина)
Алгебраическая нормальная форма, полином Жегалкина — это форма представления логической функции в виде полинома с коэффициентами вида 0 и 1, в котором в качестве произведения используется операция конъюнкции, а в качестве сложения — исключающее ИЛИ.
Примеры полиномов Жегалкина: 1, a, a⊕b, ab⊕a⊕b⊕1
Алгоритм построения СДНФ для булевой функции
Алгоритм построения СКНФ для булевой функции
Алгоритм построения полинома Жегалкина булевой функции
Есть несколько методов построения полинома Жегалкина, в данной статье рассмотрим наиболее удобный и простой из всех.
Примеры построения различных представлений логических функций
Построим совершенные дизъюнктивную и дизъюнктивную нормальные формы, а также полином Жегалкина для функции трёх переменных F = ¬a b∨ ¬b c∨ca
1. Построим таблицу истинности для функции
| a | b | c | ¬a | ¬a ∧b | ¬b | ¬b ∧c | ¬a ∧b∨ ¬b ∧c | c∧a | ¬a ∧b∨ ¬b ∧c∨c∧a |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
Построение совершенной дизъюнктивной нормальной формы:
Найдём наборы, на которых функция принимает истинное значение: < 0, 0, 1 > < 0, 1, 0 > < 0, 1, 1 > < 1, 0, 1 >
В соответствие найденным наборам поставим элементарные конъюнкции по всем переменным, причём если переменная в наборе принимает значение 0, то она будет записана с отрицанием:
Объединим конъюнкции с помощью дизъюнкции и получим совершенную дизъюнктивную нормальную форму:
Построение совершенной конъюнктивной нормальной формы:
Найдём наборы, на которых функция принимает ложное значение: < 0, 0, 0 > < 1, 0, 0 >
В соответствие найденным наборам поставим элементарные дизъюнкции по всем переменным, причём если переменная в наборе принимает значение 1, то она будет записана с отрицанием:
Объединим дизъюнкции с помощью конъюнкции и получим совершенную конъюнктивную нормальную форму:
Построение полинома Жегалкина:
Добавим новый столбец к таблице истинности и запишем в 1, 3, 5 и 7 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 2, 4, 6 и 8 сложим по модулю два со значениями из соответственно 1, 3, 5 и 7 строк:
| a | b | c | F | 1 | |
| 0 | 0 | 0 | 0 | → | 0 |
| 0 | 0 | 1 | 1 | ⊕ 0 | 1 |
| 0 | 1 | 0 | 1 | → | 1 |
| 0 | 1 | 1 | 1 | ⊕ 1 | 0 |
| 1 | 0 | 0 | 0 | → | 0 |
| 1 | 0 | 1 | 1 | ⊕ 0 | 1 |
| 1 | 1 | 0 | 0 | → | 0 |
| 1 | 1 | 1 | 1 | ⊕ 0 | 1 |
Добавим новый столбец к таблице истинности и запишем в 1 и 2, 5 и 6 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 3 и 4, 7 и 8 сложим по модулю два со значениями из соответственно 1 и 2, 5 и 6 строк:
| a | b | c | F | 1 | 2 | |
| 0 | 0 | 0 | 0 | 0 | → | 0 |
| 0 | 0 | 1 | 1 | 1 | → | 1 |
| 0 | 1 | 0 | 1 | 1 | ⊕ 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | ⊕ 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | → | 0 |
| 1 | 0 | 1 | 1 | 1 | → | 1 |
| 1 | 1 | 0 | 0 | 0 | ⊕ 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | ⊕ 1 | 0 |
Добавим новый столбец к таблице истинности и запишем в 1 2, 3 и 4 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 5, 6, 7 и 8 сложим по модулю два со значениями из соответственно 1, 2, 3 и 4 строк:
| a | b | c | F | 1 | 2 | 3 | |
| 0 | 0 | 0 | 0 | 0 | 0 | → | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | → | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | → | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | → | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | ⊕ 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 | ⊕ 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | ⊕ 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | ⊕ 1 | 1 |
Окончательно получим такую таблицу:
| a | b | c | F | 1 | 2 | 3 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 |
Выпишем наборы, на которых получившийся вектор принимает единичное значение и запишем вместо единиц в наборах имена переменных, соответствующие набору (для нулевого набора следует записать единицу):
Объединяя полученные конъюнкции с помощью операции исключающего или, получим полином Жегалкина: c⊕b⊕bc⊕ab⊕abc
Programforyou — это сообщество, в котором Вы можете подтянуть свои знания по программированию, узнать, как эффективно решать те или иные задачи, а также воспользоваться нашими онлайн сервисами.