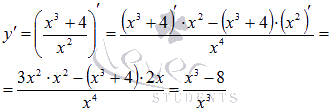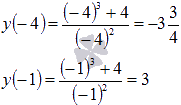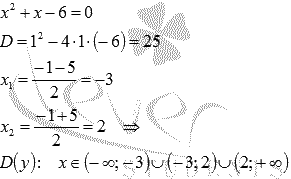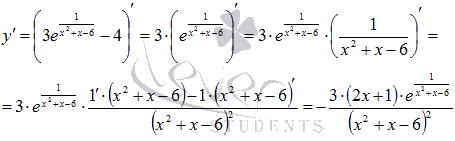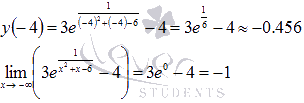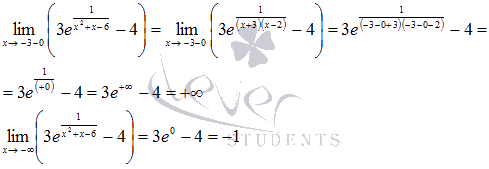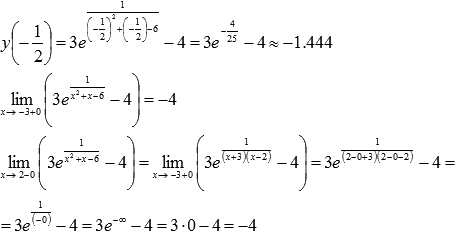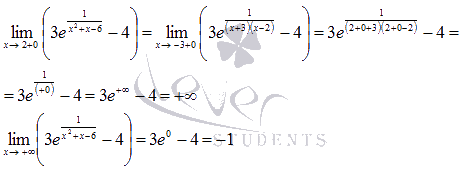Что такое наибольшее и наименьшее значение
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.
теория по математике 📈 функции
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.
На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом. Внимание!
Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Таким образом, мы нашли нуль функции: х=2
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
1. Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
Теория:
Наибольшее и наименьшее значения функции можно найти по графику функции. Иногда это значения удаётся найти, используя свойства функции. В общем случае наибольшее и наименьшее значения функции находятся с помощью производной. Для этого сформулируем некоторые теоремы.
1. Если функция непрерывна на отрезке, то она достигает на нём и своего наибольшего, и своего наименьшего значений (Эта теорема доказывается в курсе высшей математики).
2. Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
3. Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в стационарной или критической точке.
Как найти наименьшее и наибольшее значения функции на отрезке?
Пусть функция \(f(x)\) напрерывна на отрезке \([a; b]\), тогда:
2. Приравниваем производную к нулю, определяем точки экстремума функции, отбираем из них те, которые принадлежат отрезку \([a; b]\).
3. Находим значения функции y = f ( x ) в отобранных точках, и в конечных точках отрезка \(a\) и \(b\); выбираем среди полученных значений наименьшее ( y наим ) и наибольшее ( y наиб ).
А что делать, если нужно найти наибольшее или наименьшее значения функции, непрерывной на интервале? Один из вариантов — графический метод, который подразумевает построение графика функции и определение наименьшего или наибольшего значения функции по нему. Однако не всегда этот способ удобен, целесообразнее использовать следующую теорему.
а) если x = x 0 — точка максимума, то y наиб = f ( x o ) ;
На рисунках продемонстрированы геометрические иллюстрации данной теоремы.
Наибольшее и наименьшее значение функции
На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно определить оптимальное значение какого-либо параметра. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.
Основные определения
Начнем, как всегда, с формулировки основных определений.
Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или наибольшее значение на некотором промежутке именно в одной из стационарных точек.
Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.
Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы может определить наибольшее или наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с бесконечным интервалом. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения. В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.
Более понятными эти моменты станут после изображения на графиках:
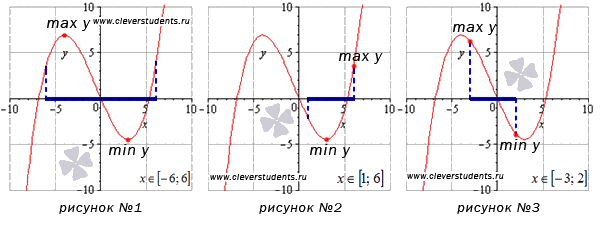
Наибольшее и наименьшее значение функции на отрезке
Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [ 1 ; 6 ] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.
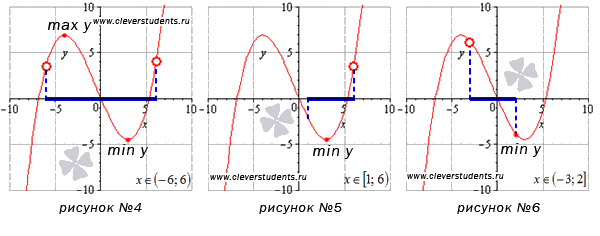
Наибольшее и наименьшее значение функции на открытом интервале
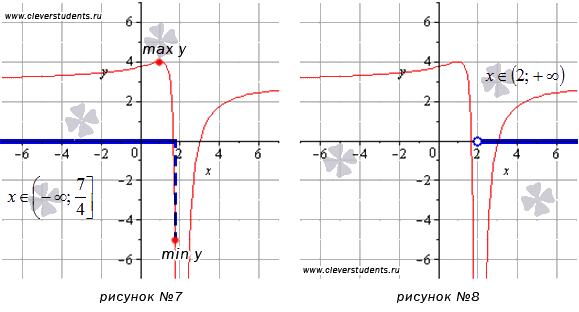
Наибольшее и наименьшее значение функции на бесконечности
Как найти наибольшее и наименьшее значение непрерывной функции на заданном отрезке
В этом пункте мы приведем последовательность действий, которую нужно выполнить для нахождения наибольшего или наименьшего значения функции на некотором отрезке.
Посмотрим, как правильно применить этот алгоритм при решении задач.
Решение:
Теперь вычисляем производную функции согласно правилу дифференцирования дроби:
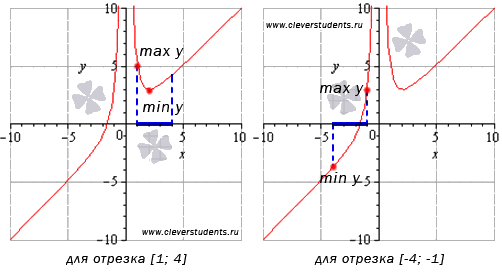
y ( 1 ) = 1 3 + 4 1 2 = 5 y ( 2 ) = 2 3 + 4 2 2 = 3 y ( 4 ) = 4 3 + 4 4 2 = 4 1 4
Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:
Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале
Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.
Решение
Первым делом находим область определения функции. В знаменателе дроби стоит квадратный трехчлен, который не должен обращаться в 0 :
Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.
Теперь выполним дифференцирование функции и получим:
Следовательно, производные функции существуют на всей области ее определения.
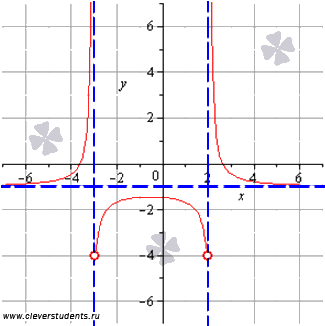
Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.
Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.
Наибольшее и наименьшее значение функции
Теория к заданию 12 из ЕГЭ по математике (профильной)
Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.
Чтобы найти наибольшее или наименьшее значение функции необходимо:
Чтобы найти точки максимума или минимума необходимо:
Таблица производных некоторых элементарных функций:
| Функция | Производная |
| $c$ | $0$ |
| $x$ | $1$ |
| $x^n, n∈N$ | $nx^ |
| $<1>/ | $-<1>/ |
| $<1>/x<^n>, n∈N$ | $- |
| $√^n | $<1>/ |
| $sinx$ | $cosx$ |
| $cosx$ | $-sinx$ |
| $tgx$ | $<1>/ |
| $ctgx$ | $-<1>/ |
| $cos^2x$ | $-sin2x$ |
| $sin^2x$ | $sin2x$ |
| $e^x$ | $e^x$ |
| $a^x$ | $a^xlna$ |
| $lnx$ | $<1>/ |
| $log_x$ | $<1>/ |
Основные правила дифференцирования
1. Производная суммы и разности равна производной каждого слагаемого
Производная суммы и разности равна производной каждого слагаемого
Наибольшее и наименьшее значение функции.
С практической точки зрения наибольший интерес представляет использование производной для нахождения наибольшего и наименьшего значения функции. С чем это связано? Максимизация прибыли, минимизация издержек, определение оптимальной загрузки оборудования. Другими словами, во многих сферах жизни приходится решать задачи оптимизации каких-либо параметров. А это и есть задачи на нахождение наибольшего и наименьшего значения функции.
Навигация по странице.
Кратко остановимся на основных определениях.
Наибольшим значением функции y=f(x) на промежутке X называют такое значение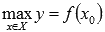 
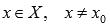
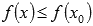
, что для любого 
справедливо неравенство 
.
Наименьшим значением функции y=f(x) на промежутке X называют такое значение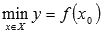 
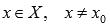
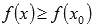
, что для любого справедливо неравенство 
.
Эти определения интуитивно понятны: наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение на рассматриваемом интервале при абсциссе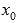 
.
Стационарные точки – это значения аргумента, при которых производная функции обращается в ноль.
Для чего нам стационарные точки при нахождении наибольшего и наименьшего значений? Ответ на этот вопрос дает теорема Ферма. Из этой теоремы следует, что если дифференцируемая функция имеет экстремум (локальный минимум или локальный максимум) в некоторой точке, то эта точка является стационарной. Таким образом, функция часто принимает свое наибольшее (наименьшее) значение на промежутке X в одной из стационарных точек из этого промежутка.
Также часто наибольшее и наименьшее значение функция может принимать в точках, в которых не существует первая производная этой функции, а сама функция определена.
Сразу ответим на один из самых распространенных вопросов по этой теме:»Всегда ли можно определить наибольшее (наименьшее) значение функции»? Нет, не всегда. Иногда границы промежутка X совпадают с границами области определения функции или интервал X бесконечен. А некоторые функции на бесконечности и на границах области определения могут принимать как бесконечно большие так и бесконечно малые значения. В этих случаях ничего нельзя сказать о наибольшем и наименьшем значении функции.
Для наглядности дадим графическую иллюстрацию. Посмотрите на рисунки – и многое прояснится.
На рисунке №3 граничные точки отрезка [-3;2] являются абсциссами точек, соответствующих наибольшему и наименьшему значению функции.
На открытом интервале
На интервале [1;6) наименьшее значение функции достигается в стационарной точке, а про наибольшее значение мы ничего сказать не можем. Если бы точка x=6 была частью интервала, тогда при этом значении функция принимала бы наибольшее значение. Этот пример изображен на рисунке №5.
Запишем алгоритм, позволяющий находить наибольшее и наименьшее значение функции на отрезке.
Разберем алгоритм при решении примера на нахождение наибольшего и наименьшего значения функции на отрезке.
Областью определения функции является все множество действительных чисел, за исключением нуля, то есть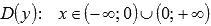 
. Оба отрезка попадают в область определения.
Находим производную функции по правилу дифференцирования дроби:
Для второго случая вычисляем значения функции лишь на концах отрезка [-4;-1] (так как он не содержит ни одной стационарной точки):
Следовательно,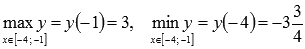 
.
Прежде чем ознакомиться с алгоритмом нахождения наибольшего и наименьшего значения функции на открытом или бесконечном интервале рекомендуем повторить определения одностороннего предела и предела на бесконечности, а также способы нахождения пределов.
Проверяем, является ли интервал X подмножеством области определения функции.
Находим все точки, в которых не существует первая производная и которые содержатся в интервале X (обычно такие точки встечаются у функций с аргументом под знаком модуля и у степенных функций с дробно-рациональным показателем). Если таких точек нет, то переходим к следующему пункту.
Если стационарных точек нет или ни одна из них не попадает в интервал, то переходим к следующему пункту.
Вычисляем значения функции в стационарных точках и точках, в которых не существует первая производная функции (если такие точки есть).
Делаем выводы, отталкиваясь от полученных значений функции и пределов. Здесь может быть масса вариантов. К примеру, если односторонний предел равен минус бесконечности (плюс бесконечности), то о наименьшем (наибольшем) значении функции ничего сказать нельзя для данного интервала. Ниже разобраны несколько типичных примеров. Надеемся подробные описания их решения помогут Вам усвоить тему. Рекомендуем вернуться к рисункам с №4 до №8 из первого раздела этой статьи.
Начнем с области определения функции. Квадратный трехчлен в знаменателе дроби не должен обращаться в ноль:
Легко проверить, что все интервалы из условия задачи принадлежат области определения функции.
Продифференцируем функцию:
Очевидно, производная существует на всей области определения функции.
Для первого промежутка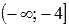 
вычисляем значение функции при x=-4 и предел на минус бесконечности:
Второй интервал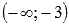 
интересен тем, что не содержит ни одной стационарной точки и ни одна из его границ не является строгой. В этом случае мы не сможем найти ни наибольшего, ни наименьшего значения функции. Вычислив предел на минус бесконечности и при стремлении аргумента к минус трем слева, мы лишь сможем определить интервал значений функции:
Следовательно, значения функции находятся в интервале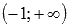 
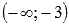
при x из промежутка .
Для интервала (-3;2) воспользуемся результатами из предыдущего пункта и еще вычислим односторонний предел при стремлении к двойке слева:
На промежутке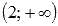 
функция не достигает ни наибольшего, ни наименьшего значения.
То есть, на этом интервале функция принимает значения из промежутка .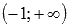
А теперь можно сопоставить полученные в каждом пункте результаты с графиком функции. Синими пунктирными линиями обозначены асимптоты.
На этом можно закончить с нахождением наибольшего и наименьшего значения функции. Алгоритмы, разобранные в этой статье, позволяют получить результаты при минимуме действий. Однако бывает полезно сначала определить промежутки возрастания и убывания функции и только после этого делать выводы о наибольшем и наименьшем значении функции на каком-либо интервале. Это дает более ясную картину и строгое обоснование результатов.