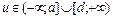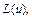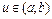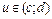Что такое нечеткое число
Часть 3. Нечеткая и лингвистическая переменные
Понятие нечеткой и лингвистической переменных используется при описании объектов и явлений с помощью нечетких множеств.
Нечеткая переменная характеризуется тройкой (α, X, А), где
α — наименование переменной;
X — универсальное множество (область определения α);
А — нечеткое множество на X, описывающее ограничения (т.е. μA(x))на значения нечеткой переменной α.
Лингвистическойпеременной (ЛП) называется набор (β, Т, X, G, М), где
β — наименование лингвистической переменной;
Т — множество ее значений (терм-множество), представляющих собой наименования нечетких переменных, областью определения каждой из которых является множество X. Множество Т называется базовым терм-множеством лингвистической переменной;
G — синтаксическая процедура, позволяющая оперировать элементами терм-множества T, в частности, генерировать новые термы (значения). Множество T∪G(T), где G(T) — множество сгенерированных термов, называется расширенным терм-множеством лингвистической переменной;
М — семантическая процедура, позволяющая превратить каждое новое значение лингвистической переменной, образуемое процедурой G, в нечеткую переменную, т.е. сформировать соответствующее нечеткое множество.
Замечание. Чтобы избежать большого количества символов:
1) символ β используют как для названия самой переменной, так и для всех ее значений;
2) пользуются одним и тем же символом для обозначения нечеткого множества и его названия, например терм «Молодой», являющийся значением лингвистической переменной β = «возраст», одновременно есть и нечеткое множество М («Молодой»).
Присвоение нескольких значений символам предполагает, что контекст позволяет разрешить возможные неопределенности.
Пример. Пусть эксперт определяет толщину выпускаемого изделия с помощью понятий «Малая толщина», «Средняя толщина» и «Большая толщина», при этом минимальная толщина равна 10 мм, а максимальная – 80 мм.
Формализация такого описания может быть проведена с помощью следующей лингвистической переменной (β, Т, X, G, М), где
β — толщина изделия;
G — процедура образования новых термов с помощью связок «и», «или» и модификаторов типа «очень», «не», «слегка» и т.п. Например: «Малая или средняя толщина», «Очень малая толщина» и т.д.;
М — процедура задания на X = [10, 80] нечетких подмножеств А1 = «Малая толщина», А2= «Средняя толщина», A3 = «Большая толщина», а также нечетких множеств для термов из G(Т)в соответствии с правилами трансляции нечетких связок и модификаторов «и», «или», «не», «очень», «слегка» и других операций над нечеткими множествами вида: А⋂В, A∪В, ̅A,CONА = A 2 , DILА = А 0,5 и т. п.
Замечание. Наряду с рассмотренными выше базовыми значениями лингвистической переменной «Толщина» (Т = <«Малая толщина», «Средняя толщина», «Большая толщина»>) возможны значения, зависящие от области определения X. В данном случае значения лингвистической переменной «Толщина изделия» могут быть определены как «около 20 мм», «около 50 мм», «около 70 мм», т.е. в виде нечетких чисел.
Терм-множество и расширенное терм-множество в условиях примера можно характеризовать функциями принадлежности, приведенными на рис. 1.5 и 1.6.
Рис. 1.5. Функции принадлежности нечетких множеств: «Малая толщина» = А1, «Средняя толщина» = А2, «Большая толщина» = А3
Рис. 1.6. Функция принадлежности нечеткого множества «Малая или средняя толщина» = A1∪ А2
Нечеткие числа
Нечеткие числа— нечеткие переменные, определенные на числовой оси, т.е. нечеткое число определяется как нечеткое множество А на множестве действительных чисел ℝс функцией принадлежности μА(х) ϵ [0, 1], где х — действительное число, т.е. х ϵ ℝ.
Множество α-уровня нечеткого числа А определяется как
Подмножество SA⊂ ℝ называется носителем нечеткого числа А, если
Нечеткое число А унимодально, если условие μА(х) = 1 справедливо только для одной точки действительной оси.
Выпуклое нечеткое число А называется нечетким нулем, если
Нечеткое число А положительно, если ∀x ϵ SA, х> 0 и отрицательно, если ∀х ϵ SA, х 0, β > 0 — левый и правый коэффициенты нечеткости.
Таким образом, при заданных L(у)и R(у) нечеткое число (унимодальное) задается тройкой А = (а, α, β).
Толерантное нечеткое число задается, соответственно, четверкой параметров А = (a1, а2, α, β), где а1 иа2 — границы толерантности, т.е. в промежутке [a1, а2] значение функции принадлежности равно 1.
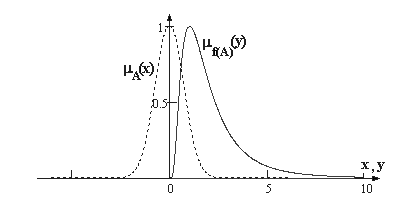
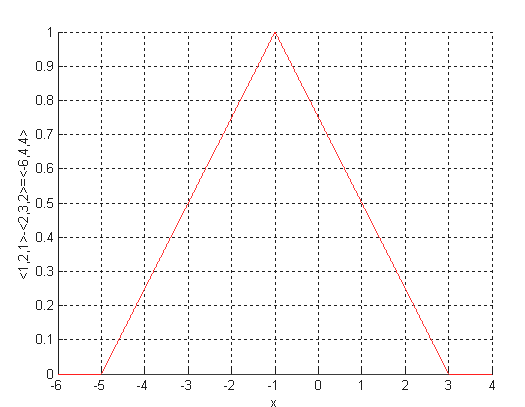
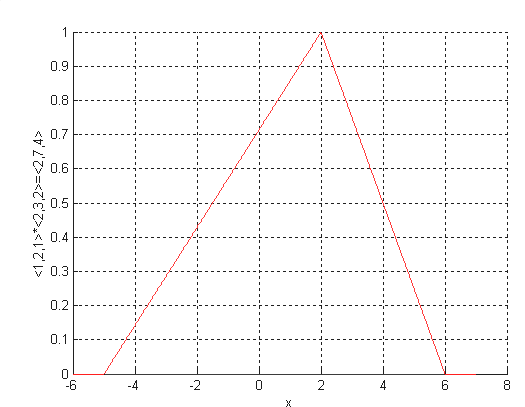
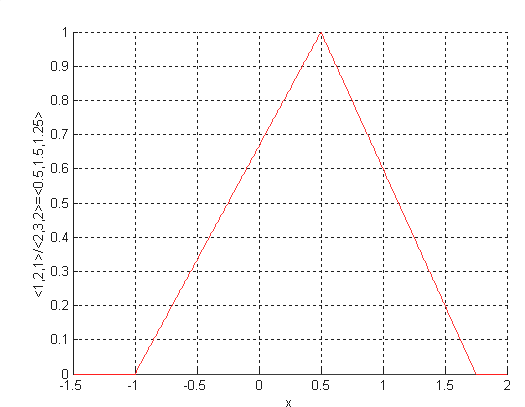
Примеры графиков функций принадлежности нечетких чисел (L-R)-типа приведены на рис. 1.8.
Рис. 1.8. Примеры графиков функций принадлежности нечетких чисел (L-R)-типа
Отметим, что в конкретных ситуациях функции L(у),R(у),а также параметры а, β нечетких чисел (а, α, β) и (a1, а2, α, β) должны подбираться таким образом, чтобы результат операции (сложения, вычитания, деления и т.д.) был точно или приблизительно равен нечеткому числу с теми же L(у)и R(у),а параметры α’ и β’ результата не выходили за рамки ограничений на эти параметры для исходных нечетких чисел, особенно если результат в дальнейшем будет участвовать в операциях.
Замечание. Решение задач математического моделирования сложных систем с применением аппарата нечетких множеств требует выполнения большого объема операций над разного рода лингвистическими и другими нечеткими переменными. Для удобства исполнения операций, а также для ввода-вывода и хранения данных, желательно работать с функциями принадлежности стандартного вида.
Нечеткие множества, которыми приходится оперировать в большинстве задач, являются, как правило, унимодальными и нормальными. Одним из возможных методов аппроксимации унимодальных нечетких множеств является аппроксимация с помощью функций (L-R)-типа.
Примеры (L-R)-представлений некоторых лингвистических переменных приведены в табл. 1.2.
Таблица 1.2. Возможное (L—R)-представление некоторых лингвистических переменных
2.5. Нечеткие числа, нечеткие отображения и нечеткие функции, принцип обобщения, арифметические операции над нечеткими числами.
Процесс управления в технических системах основывается на количественном представлении сигналов в рассматриваемой системе. Такое представление связано с рассмотрением нечетких отображений, нечетких функций, а также специальных нечетких множеств, которые задаются на множестве действительных чисел и служат аналогом обычных чисел, рассматриваемых в контексте четких (обычных) множеств.
С лингвистической точки зрения нечеткое число – это нечеткая величина, трактуемая как неточное, неопределенное числовое значение некоторой измеримой величины: например, «примерно три», «приблизительно семь» и т.п.
Нечеткий интервал – это нечеткая величина с выпуклой функцией принадлежности.
Нечеткое число – это нечеткая величина с выпуклой унимодальной функцией принадлежности. Другими словами, нечеткое число соответствует унимодальному выпуклому нечеткому множеству, заданному на универсальном множестве действительных чисел.
Нечеткий нуль – это нечеткое число с нулевым модальным значением.
Положительное (отрицательное) нечеткое число – это нечеткое число со строго положительным (отрицательным) носителем.
Поскольку нечеткие числа и интервалы представляют собой нечеткие множества, то для них справедливы все свойства и операции, введенные ранее для нечетких множеств..
Данное выше классическое определение отображения в теории нечетких множеств принято называть четким отображением, поскольку наряду с ним по аналогии можно ввести понятие нечеткого отображения или нечеткой функции.
Пример. На множествах X = 1 ; 2 ; 3 и Y = 1 ; 5 задано нечеткое отображение f : X → Y посредством нечеткой функции
Принцип обобщения распространяет понятие «отображение» математического анализа и соответственно математические операции типа сложения, вычитания, умножения, деления и др. на описываемые нечеткими множествами нечеткие числа, Введение принципа обобщения дает возможность, оперируя нечеткими числами, решать при наличии лингвистически заданной неопределенности традиционные задачи теории управления: идентификации, фильтрации, прогнозирования и т.д.Классическое определение принципа обобщения, введенное Заде, выглядит следующим образом.
Пример. Пусть нечетким множеством A = 0,1 / x 1 + 0,7 / x 2 + 1 / x 3 + 0,6 / x 4 задано нечеткое число. Задана нечеткая функция f (нечеткое отображение) посредством определения двуместной функции принадлежности:
Для x 1 множества A и каждого y i функции отображения :
Для всех множеств точек нечеткого отображения по каждому y i ищем верхние границы и получаем:
Пример. Заданы два нечетких числа: A = 0,1 / 1 + 1 / 2 + 0,2 / 3 – «вероятно два»; B = 0,2 / 2 + 0,5 / 3 + 1 / 4 + 0,4 / 5 + 0,1 / 6 – «наверное четыре». Согласно принципу обобщения попарно над всеми элементами каждого из множеств проводится соответствующая арифметическая операция, при этом оставляется наименьшая из степеней принадлежности каждой пары аргументов (рис.2.16). Далее для всех одинаковых результатов алгебраической операции, полученных при их парном выполнении, выбирается наибольшая из степеней принадлежности каждого из массива равных аргументов.
Рис.2.16. Граф арифметической операции над нечеткими числами
Посчитаем результат операции «вероятно два»+«наверное четыре» или A + B ar :
Посчитаем результат операции «вероятно два»-«наверное четыре» или A − B ar :
Посчитаем результат операции «вероятно два»*«наверное четыре» или A ∗ B ar :
Посчитаем результат операции «вероятно два»/«наверное четыре» или A / B ar :
Нечеткое число (L—R)-типа – это нечеткая величина A = μ A x / x с функцией принадлежности в виде композиции функций L-R отображения:
Частный случай – обратное значение положительного нечеткого числа
Нечеткий интервал (L—R)-типа – это нечеткая величина A = μ A x / x с функцией принадлежности в виде композиции функций
Логичным продолжением введенных выше понятий нечетких функций и нечетких чисел является концепция нечеткой и лингвистической переменных, которая широко используется в нечетком управлении.
Лингвистическая переменная является обобщением понятия нечеткой переменной и определяется кортежем параметров где:
Наряду с базовыми значениями лингвистической переменной (например, «малая температур»), возможны другие значения, зависящие от конкретного значения x (например, «около 50 ° C »). Такие значения лингвистической переменной удобно представлять в виде нечетких чисел.
При представлении различных термов тех или иных лингвистических переменных нечеткими числами рекомендуется придерживаться следующих правил:
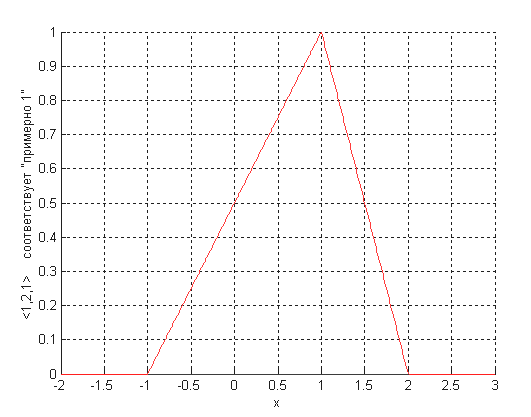
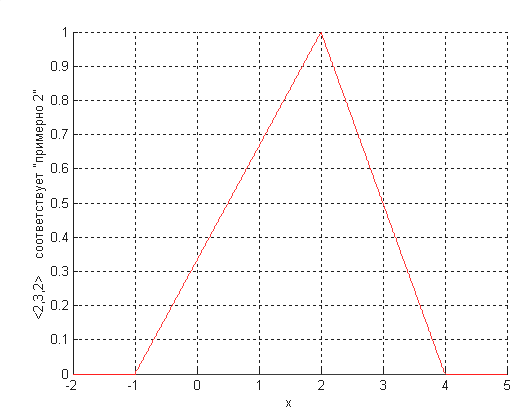
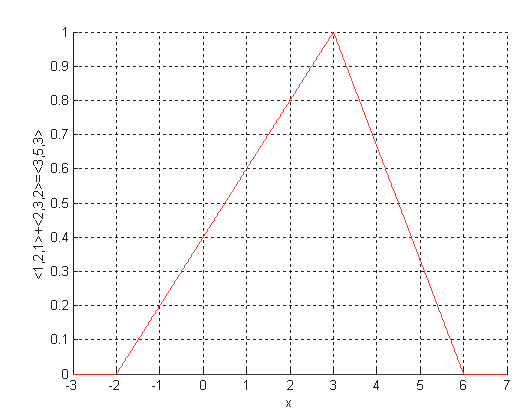
Пример. Нечеткие числа «приблизительно один» и «приблизительно два», а также четыре основных алгебраических операции над ними будут выглядеть согласно рис 2.17.
Замечание. В самом общем случае принцип обобщения, составляющий основу нечеткой арифметики, задается соотношением где F – функция, определяющая произвольную операцию пересечения. В современной теории нечетких множеств наиболее полно исследован комплекс операций, связанных с аксиоматическим введением операции пересечения видаЭтот подход был заимствован из традиционной теории множеств. Однако в настоящее время ведутся разработки методов теории нечетких множеств, основанных на аксиоматике, базирующейся на операциях алгебраического и среднего геометрического пересечения:
Все отмеченные альтернативные варианты введения операции пересечения нечетких множеств с определенной степенью точности соответствуют описанию классических операций над обычными множествами. Поэтому выбор того или иного подхода зависит от конкретной задачи, что в свою очередь позволяет в разной степени учесть разнообразные смысловые оттенки лингвистических нечетких понятий и приводит к разным результатам при моделировании реальных процессов и управлении сложными динамическими системами.
Что такое нечеткое число
Нечеткое число — это нечеткое подмножество универсального множества действительных чисел, имеющее нормальную и выпуклую функцию принадлежности, то есть такую, что: а) существует значение носителя, в котором функция принадлежности равна единице, а также b) при отступлении от своего максимума влево или вправо функция принадлежности не возрастает.
0\>.» src=»http://rgguapsis.narod.ru/Tuljakoff/misc/NechetkieM/7.files/6c3dd3516ec6fb3a49216c3c07596ac3.png» width=159>
Согласно принципу обобщения Заде было введено понятие арифметических операций на множестве нечетких чисел. Для произвольных нечетких чисел и для любых чисел справедливо
Расширенные бинарные арифметические операции (сложение, умножение и пр.) для нечетких чисел определяются через соответствующие операции для четких чисел с использованием принципа обобщения следующим образом:
Анализ свойств арифметических операций над нечеткими числами показал, что нечеткое число не имеет противоположного и обратного чисел, сложение и умножение коммутативны, ассоциативны и в общем случае недистрибутивны.
Нечеткие числа (L-R)-типа — это разновидность нечетких чисел специального вида, т.е. задаваемых по определенным правилам с целью снижения объема вычислений при операциях над ними.
где — мода; 0″ src=»http://rgguapsis.narod.ru/Tuljakoff/misc/NechetkieM/7.files/b394a911c7c919a70370578171c8a785.png» width=49>, 0″ src=»http://rgguapsis.narod.ru/Tuljakoff/misc/NechetkieM/7.files/65eb8705d9dcdeb730697781fd698ac7.png» width=49> — левый и правый коэффициенты нечеткости.
Нечеткие треугольные числа
Определение. Треугольным нечетким числом называется тройка действительных чисел, через которые его функция принадлежности определяется следующим образом:
К сожалению, даже при ограничении нашего виденья нечетких чисел до понятия треугольных чисел, проблемы противоположного, обратного элементов и дистрибутивности остаются нерешенными.
Есть еще один существенный недостаток такого подхода. Размытость произведения зависит не только от размытости сомножителей, но и от того, какое место данные нечеткие числа занимают на числовой оси. Например, пусть
Это позволило авторам ввести понятие меры и превратить множество нечетких чисел в топологическое пространство.
Далее вводится понятие арифметических операций над нечеткими числами такого вида. Для любых нечетких чисел и они определяются следующим образом:
Этот подход позволяет решить проблему дистрибутивности, так как размытость числа для всех четырех операций вычисляется при помощи единственногооператора, который дистрибутивен относительно самого себя (т.е. коммутативен, ассоциативен и идемпотентен).
Несмотря на это преимущество, проблемы противоположного и обратного элементов и при таком подходе остаются нерешенными.
Четкие арифметики нечетких треугольных чисел
Определяя операции сложения и умножения, мы можем вычислять размытость суммы и произведения нечетких треугольных чисел либо по одному алгоритму, либо по разным. Сперва рассмотрим случай, когда размытость суммы и произведения нечетких треугольных чисел вычисляется по одному алгоритму. Определим операции сложения и умножения нечетких треугольных чисел следующим образом:
где — либо сложение, либо умножение, — некоторая бинарная операция, определенная на множестве неотрицательных действительных чисел.
Опишем, какими свойствами должна обладать операция для того, чтобы сложение и умножение были коммутативны, ассоциативны, дистрибутивны, а также существовали противоположные и обратные элементы.
Очевидно, что для того, чтобы операция была коммутативной и ассоциативной, также должна быть коммутативной и ассоциативной, т.е. удовлетворять следующим условиям:
Аналогично, если — нечеткая единица, то для любого имеем
Для того, чтобы операции удовлетворяли условию дистрибутивности, необходимо и достаточно, чтобы для любых операция удовлетворяла следующему условию:
Если коммутативна и ассоциативна, то получим
Следовательно, для того, чтобы условие (2) выполнялось, достаточно, чтобы была коммутативна, ассоциативна и идемпотентна, т.е. удовлетворяла условиям (1) и для любого
Нетрудно показать, что никакая группа не обладает свойством идемпотентности.
Невозможно построить арифметику нечетких треугольных чисел, изоморфную арифметике действительных (четких) чисел, если размытость суммы и произведения нечетких треугольных чисел вычисляется по одному алгоритму.
Теперь рассмотрим случай, когда размытость суммы и произведения определяются по разным алгоритмам. Пусть
Очевидно, что если алгебраическая система удовлетворяет свойствам коммутативности, ассоциативности, дистрибутивности, существования нейтрального и единичного элементов, существования противоположного и обратного элементов, то она образует ассоциативное, коммутативное кольцо с единицей и с делением (т.е. почти поле).
Таким образом, мы получим
Недостатком этой арифметики является то, что в нее не входят четкие и «получеткие» числа, т.е. числа, у которых хотя бы один из коэффициентов размытости равен нулю. Но этого легко избежать, если доопределить ее, например, следующим образом:
Заметим, что, варьируя мощность изоморфного поля, мы тем самым варьируем и мощность множества коэффициентов размытости, используемых в данной арифметике.
Размытые арифметики нечетких треугольных чисел
В предыдущем параграфе мы доказали, что возможно построить арифметику нечетких треугольных чисел, аналогичную арифметике четких чисел. Однако, на наш взгляд, каждая такая арифметика будет обладать одним существенным недостатком.
Если имеет некоторое лингвистическое значение (например, «приблизительно «), то нечеткое число является некоторым модификатором числа (например, «болееили менее приблизительно «). Таким образом, нечеткое число является «приблизительно нулевым элементом». Более того, при и эта «приблизительность» возрастает. Однако при формальном описании арифметики это свойство нигде не отражается.
Рассмотрим новый подход к арифметике нечетких чисел, который успешно формализует описанное выше свойство без потери свойств, аналогичных свойствам четкой арифметики. При этом подходе нечеткость рассуждений увеличивается, но это не всегда является минусом.
Если ЧА-НТЧ обладает свойством коммутативности, то РА-НТЧ будет обладать сильным свойством коммутативности, т.е. для любых выполняется
Прежде чем говорить об ассоциативности и дистрибутивности, необходимо рассмотреть алгоритм вычисления арифметических выражений, содержащих более двух нечетких треугольных чисел.
Нетрудно убедиться, что полученная арифметика будет обладать свойствами слабой ассоциативности и слабой дистрибутивности, т.е. для любых выполнены следующие равенства множеств:
Понятие нечеткого числа
Одной из областей применение нечеткой логики является выполнение арифметических операций с нечеткими множествами. Для снижения трудоемкости таких операций используется специальный тип нечетких множеств – нечеткие числа.
Нечетким числом(НЧ) называется нечеткая переменная, имеющая следующие свойства: 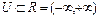
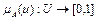
Другими словами, нечеткое число– именованное нечеткое множество, для которого универсальное множество U представляет собой интервал действительной оси R.
В реальных задачах используются кусочно-линейные нечеткие числа.Для упрощения арифметических операций кусочно-линейные функции принадлежности дополнительно аппроксимируют, чтобы получить специальный вид нечетких чисел – параметрические нечеткие числа или нечеткие числа
(L–R)–типа, которые характеризуются компактностью представления и просто-
той реализации арифметических операций.
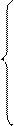
0,
|
1, 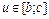
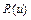
где 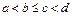
Нечеткое параметрическое число обозначается (a, b, c, d)LR.
Таким образом, нечеткое число (L–R)–типа описывается шестью параметрами: четырьмя числами, обозначающими его границы, и двумя функциями, определяющими форму его функции принадлежности.
 |
Рис.7.8 Параметрические нечеткие числа
Нечеткое числоназывается унимодальным, если оно имеет только одну точку, в которой функция принадлежности равна единице, т.е. его параметры b и c равны, в противном случае нечеткое число называется толерантным (см. рис. 7.8). Унимодальные нечеткие числа обозначаются пятью параметрами (a, b, d)LR.
В качестве LR–функций наиболее часто используют линейные зависимости, задаваемые следующими соотношениями:
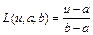
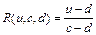
LR – функции также могут задаваться квадратичными, экспоненциальными и другими зависимостями.
В случае использования линейных функций унимодальные и толерантные нечеткие числа называют соответственно треугольными и трапециевидными и обозначают (a, b, d) и (a, b, c, d).
Для нечетких чисел особым образом определяется понятие знака и нулевого значения.
Нечеткое число А называется положительным, если его основание лежит в положительной действительной полуоси 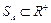
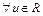
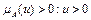
Нечеткое число А называется отрицательным, если его основание лежит в отрицательной действительной полуоси 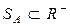
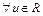
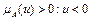
Для параметрических нечетких чисел знак определяется значениями параметров: положительное нечеткое число, если a > 0; отрицательное, если d
Дата добавления: 2016-04-22 ; просмотров: 1509 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ