Что такое неотрицательное число в математике
Какие числа называются целыми
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение целых чисел
Что важно знать о целых числах:
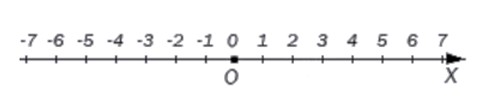
Целые числа на числовой оси выглядят так:
На координатной прямой начало отсчета всегда начинается с точки 0. Слева находятся все отрицательные целые числа, справа — положительные. Каждой точке соответствует единственное целое число.
В любую точку прямой, координатой которой является целое число, можно попасть, если отложить от начала координат данное количество единичных отрезков.
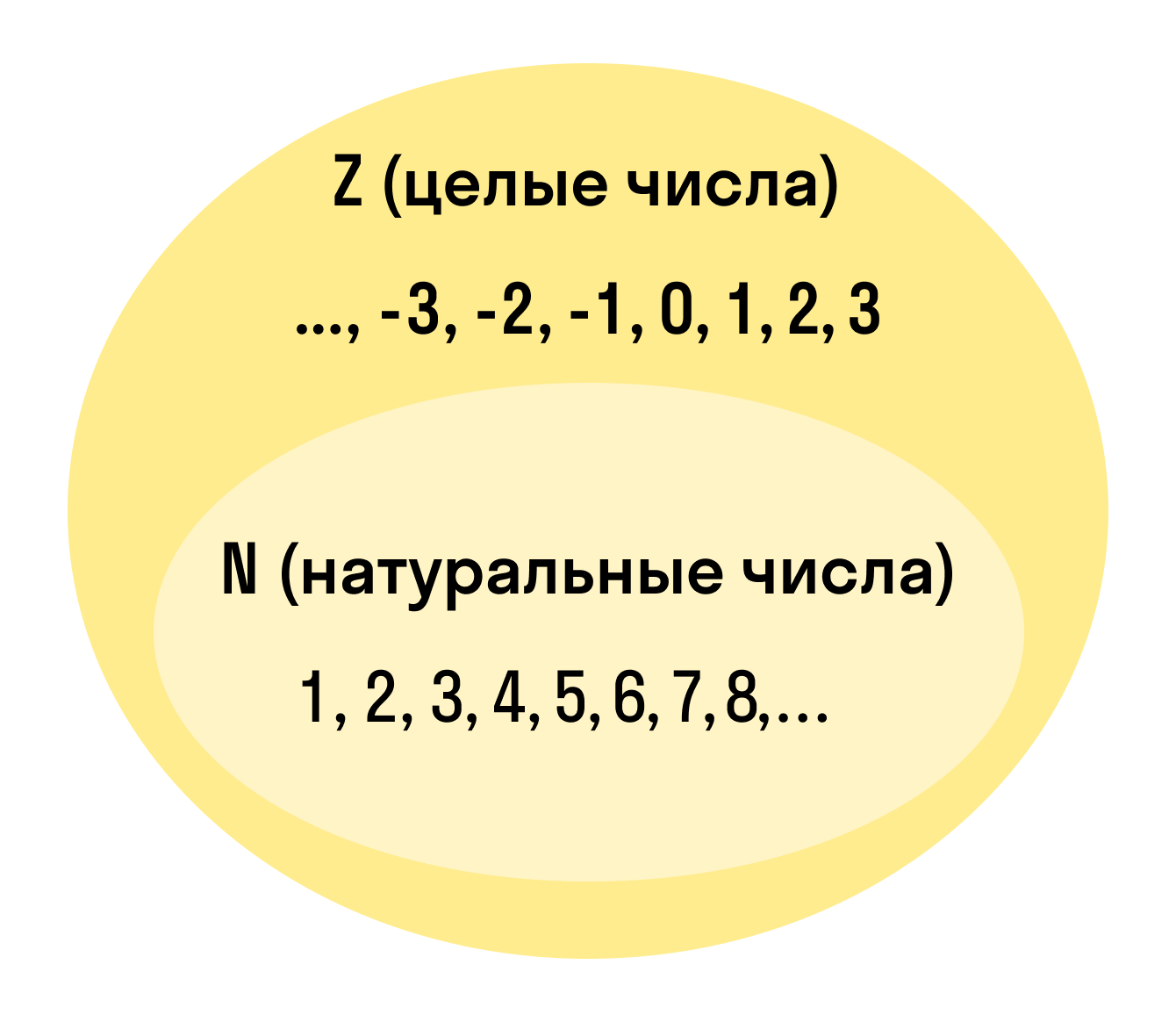
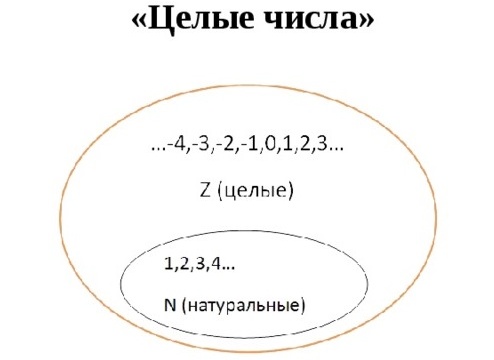
Натуральные числа — это целые, положительные числа, которые мы используем для подсчета. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.
Целые числа — это расширенное множество натуральных чисел, которое можно получить, если добавить к ним нуль и отрицательные числа. Множество целых чисел обозначают Z.
Выглядит эти ребята вот так:
Последовательность целых чисел можно записать так:
Свойства целых чисел
Таблица содержит основные свойства сложения и умножения для любых целых a, b и c:
Целые числа: общее представление
В данной статье определим множество целых чисел, рассмотрим, какие целые называются положительными, а какие отрицательными. Также покажем, как целые числа используются для описания изменения некоторых величин. Начнем с определения и примеров целых чисел.
Целые числа. Определение, примеры
Определение 1. Целые числа
Целые числа и координатная прямая
Пусть координатная прямая проведена горизонтально и направлена вправо. Взглянем на нее, чтобы наглядно представить расположение целых чисел на прямой.
В любую точку прямой, координатой которой является целое число, можно попасть, отложив от начала координат некоторое количество единичных отрезков.
Положительные и отрицательные целые числа
Из всех целых чисел логично выделить положительные и отрицательные целые числа. Дадим их определения.
Определение 2. Положительные целые числа
Определение 3. Отрицательные целые числа
Число 0 разделяет положительные и отрицательные целые числа и само не является ни положительным, ни отрицательным.
Любое число, противоположное положительному целому числу, в силу определения, является отрицательным целым числом. Справедливо и обратное. Число, обратное любому отрицательному целому числу, есть положительное целое число.
Можно дать другие формулировки определений отрицательных и положительных целых чисел, используя их сравнение с нулем.
Определение 4. Положительные целые числа
Соответственно, положительные числа лежат правее начала отсчета на координатной прямой, а отрицательные целые числа находятся левее от нуля.
Неположительные и неотрицательные целые числа
Определение 6. Неотрицательные целые числа
Как видим, число нуль не является ни положительным, ни отрицательным.
Использование целых чисел при описании изменения величин
Для чего используются целые числа? В первую очередь, с их помощью удобно описывать и определять изменение количества каких-либо предметов. Приведем пример.
Пусть на складе хранится какое-то количество коленвалов. Если на склад привезут еще 500 коленвалов, то их количество увеличится. Число 500 как раз и выражает изменение (увеличение) количества деталей. Если потом со склада увезут 200 деталей, то это число также будет характеризовать изменение количества коленвалов. На этот раз, в сторону уменьшения.
Если же со склада ничего не будут забирать, и ничего не будут привозить, то число 0 укажет на неизменность количества деталей.
Очевидное удобство использования целых чисел в отличие от натуральных в том, что их знак явно указывает на направление изменения величины (увеличение или убывание).
Целые числа. Определение.
Существуют множество разновидностей чисел, одни из них – это целые числа. Целые числа появились для того, чтобы облегчить счет не только в положительную сторону, но и в отрицательную.
Ряд целых чисел.
Этот ряд чисел называется рядом целых чисел.
Целые положительные числа. Целые отрицательные числа.
Ряд целых чисел состоит из положительных и отрицательных чисел. Справа от нуля идут натуральные числа или их еще называют целыми положительными числами. А слева от нуля идут целые отрицательные числа.
Нуль не является ни положительным ни отрицательным числом. Он является границей между положительными и отрицательными числами.
Целые числа – это множество чисел, состоящие из натуральных чисел, целых отрицательных чисел и нуля.
Ряд целых чисел в положительную и в отрицательную сторону является бесконечным множеством.
Если мы возьмём два любых целых числа, то числа, стоящие между этими целыми числами, будут называться конечным множеством.
Натуральные числа обозначаются латинской буквой N.
Целые числа обозначаются латинской буквой Z. Все множество натуральных чисел и целых чисел можно изобразить на рисунке. 
Неположительные целые числа другими словами – это отрицательные целые числа.
Неотрицательные целые числа – это положительные целые числа.
Вопросы по теме:
Как называются числа, находящиеся в ряду целых чисел: а) справа от нуля; б) слева от нуля?
Ответ: а) натуральные числа или целые положительные числа. Оба термина несут один и тот же смысл.
б) целые отрицательные числа.
Назовите наибольшее целое число?
Ответ: ряд положительных целых чисел бесконечен, поэтому наибольшего целого числа не существует.
Какое наименьшее целое число?
Ответ: ряд отрицательных чисел бесконечен, поэтому наименьшего целого числа не существует.
Целые числа
Что такое целые числа
Целые числа — это множество натуральных чисел, отрицательных и нуль.
Другими словами определение можно сформулировать так: целые числа — такие, у которых нет дробной части. Любое натуральное число считается целым, но не любое целое является натуральным.
-98; 24; 0; 3; 4512 — это все целые числа.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Целые числа имеют обозначение в виде знака Z (от нем. названия Zahlen — «числа»). Им присущи три базовые арифметические операции:
А также можно провести специфическую операцию — деление с остатком.
Использование целых чисел при описании изменения величин
Изменение величин каких-либо предметов или объектов удобнее всего описывать с помощью целых чисел. Именно они со своими знаками «+» или «-» наглядно показывают увеличение/уменьшение величины или же ее неизменность, если использовать 0. В этом выражении заключается одно из главных отличий множества целых чисел от натуральных.
Для наглядности можно привести пример, который покажет, как вычислить изменение величин:
На полке хранилось некое количество книг. Затем к ним поставили 10 новых экземпляров. Параметр 10 означает изменение (увеличение, «+») количества предметов. Если с полки потом уберут 5 книг, то этот показатель тоже будет выражать изменение количества предметов, но уже в сторону уменьшения (значение знака «-»).
Если же на полку не поставят новые книги и не заберут старые, то число 0 окажется индикатором неизменности количества предметов.
Кроме того, понятие о целых числах используется не только в алгебре, но и в таких областях, как география, история, медицина, физика.
Положительные и отрицательные целые числа
Положительные целые числа — это числа, которые отмечаются знаком «плюс». К примеру, к ним относятся: 1; 2; 3; 4.
Свойство нуля состоит в том, что он не принадлежит ни к положительным, ни к отрицательным. Оно их разделяет.
Для любого положительного целого числа существует единственное противоположное отрицательное. Справедливо и обратное правило. 0 противоположен самому себе.
Неположительные и неотрицательные целые числа
Неотрицательные целые числа — это положительные целые числа и нуль. К ним можно отнести числа типа 54; 146; 0.
По другому, неположительными целыми числами считают те, которые меньше или равны нулю. И наоборот, неотрицательные те, которые больше или равны нулю.
Данные термины ввели для удобства изъяснения. Для того, чтобы не говорить, что число n — меньше или равно нулю, можно сократить фразу и сказать: число n — целое неположительное.
Неотрицательное число
Отрицательное число — элемент множества отрицательных чисел, которое (вместе с нулём) появилось в математике при расширении множества натуральных чисел. Цель расширения: обеспечить выполнение операции вычитания для любых чисел. В результате расширения получается множество (кольцо) целых чисел, состоящее из положительных (натуральных) чисел, отрицательных чисел и нуля.
Все отрицательные числа, и только они, меньше, чем нуль. На числовой оси отрицательные числа располагаются слева от нуля. Для них, как и для положительных чисел, определено отношение порядка, позволяющее сравнивать одно целое число с другим.
Содержание
Свойства отрицательных чисел
Отрицательные числа подчиняются практически тем же правилам, что и натуральные, но имеют некоторые особенности.
Исторический очерк
Древний Египет, Вавилон и Древняя Греция не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные.
Впервые отрицательные числа были частично узаконены в Китае, а затем (примерно с VII века) и в Индии, где трактовались как долги (недостача), или признавались как промежуточный этап, полезный для вычисления окончательного, положительного результата. Правда, умножение и деление для отрицательных чисел тогда ещё не были определены.
Диофант в III веке уже знал правило знаков и умел умножать отрицательные числа. Однако и он рассматривал их лишь как временные значения.
В XVII веке, с появлением аналитической геометрии, отрицательные числа получили наглядное геометрическое представление на числовой оси. С этого момента наступает их полное равноправие. Тем не менее теория отрицательных чисел долго находилась в стадии становления. Оживлённо обсуждалась, например, странная пропорция 1:(-1) = (-1):1 — в ней первый член слева больше второго, а справа — наоборот, и получается, что большее равно меньшему («парадокс Арно»). Непонятно было также, какой смысл имеет умножение отрицательных чисел, и почему произведение отрицательных положительно; на эту тему проходили жаркие дискуссии.
Полная и вполне строгая теория отрицательных чисел была создана только в XIX веке (Уильям Гамильтон и Герман Грассман).