Что такое несмежные вершины

Многоугольник

Определение 1. Многоугольник − замкнутая ломаная линия.

Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:

Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.

Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.

Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.

Виды многоугольников

Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с \( \small n \) вершинами называется \( \small n- \)угольником.

На рисунке 1 представлены различные виды многоугольников.

Обозначение многоугольника

Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют \( \small A_1A_2A_3A_4A_5A_6 \) или \( \small A_6A_5A_4A_3A_2A_1 \).

Соседние вершины многоугольника

Вершины многоугольника называются соседними, если они являются концами одной из его сторон.

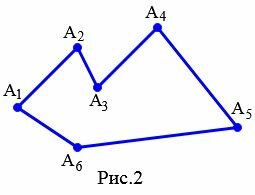На рисунке 2 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)

Смежные стороны многоугольника

Стороны многоугольника называются смежными, если они имеют общую вершину.

На рисунке 2 стороны \( \small A_4A_5 \) и \( \small A_5A_6 \) являются смежными, так как они имеют общую вершину \( \small A_5. \)

Простой многоугольник. Самопересекающийся многоугольник

Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).

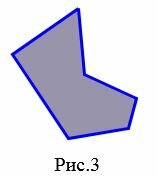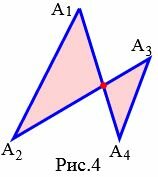На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой многоугольник называется самопересекающийся многоугольник.

Выпуклый многоугольник

Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.

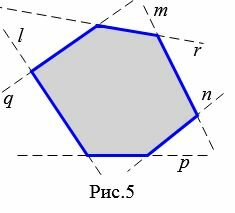На рисунке 5 многоугольник лежит по одну сторону от прямых \( \small m, \ n, \ l, \ p, \ q, \ r\) проходящих через стороны многоугольника.

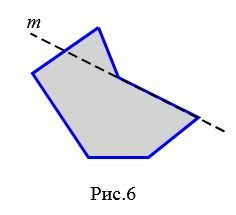На рисунке 6 прямая \( \small m\) делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой \( \small m\). Следовательно многоугольник не является выпуклым.

Правильный многоугольник

Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.

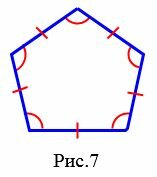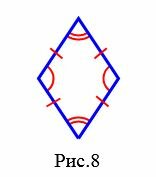На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.

Звездчатый многоугольник

Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.

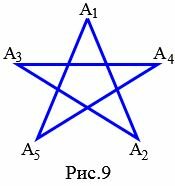На рисунке 9 представлен звездчатый пятиугольник поскольку все углы \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) равны и равны все стороны: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)

Периметр многоугольника

Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника \( \small A_1A_2. A_A_n \) периметр вычисляется из формулы:

Угол многоугольника

Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small A_3 \) на рисунке 2).

Внешний угол многоугольника

Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.

На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине \( \small E. \)

Диагональ многоугольника. Количество диагоналей

Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.

Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:

Сумма углов выпуклого многоугольника

Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины \( \small A_1 \) все диагноали многоугольника \( \small A_1A_2. A_A_n \) (Рис.11):

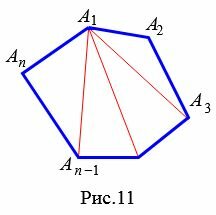Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно \( \small n-3 \). Следовательно, эти диагонали разделяют многоугольник на \( \small n-3+1=n-2 \) треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: \( \small 180°(n-2). \)

где \( \small n \) −количество сторон (вершин) выпуклого многоугольника.

Угол правильного многоугольника

Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:

где \( \small n \) −количество сторон (вершин) правильного многоугольника.

Источник

Теория Графов. Часть 2 Смежность, инцидентность, петли

Ничего не сделано, если что-то осталось недоделанным. – Иоганн Гаусс

Смежность и инцидентность

Смежность и инцидентность

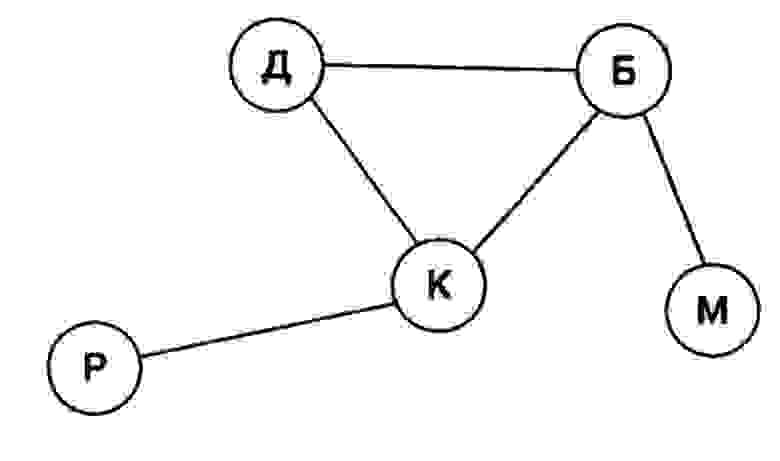
Давайте рассмотрим самый обыкновенный неориентированный граф (Рисунок 1). В нем есть вершина Р и вершина К. Данные вершины являются смежными (adjacent), так как они соединены ребром РК.

Помимо этого, как мы видим, вершина К является концом ребра РК, а Р его началом, в таких случаях вершина К и Р называются инцидентными (incident) ребру РК.

Рисунок 1

Смежностью вершин графа – называется отношение между двумя вершинами, в котором существует ребро их соединяющее.

Инцидентность – это когда вершина a является началом или концом ребра t. Если мы добавим еще одну вершину b, то мы скажем, что вершина a и b инцидента ребру t.

Кроме вершин, смежность присутствует и у рёбер. Рёбра просто должны иметь общую вершину. В нашем случаи мы можем сказать, что ребро ДК является смежным ребру РК, так как у них есть общая вершина К.

Смежностью рёбер графа – называется отношение между двумя рёбрами, в котором существует вершина соединяющая их.

В связи с тем, что выше мы рассматривали неориентированный граф, то было неважно, с какого направления определять смежность и инцидентность. Вершина Р могла быть смежна вершине К, но также мы могли сказать, что вершина К смежна вершине Р.

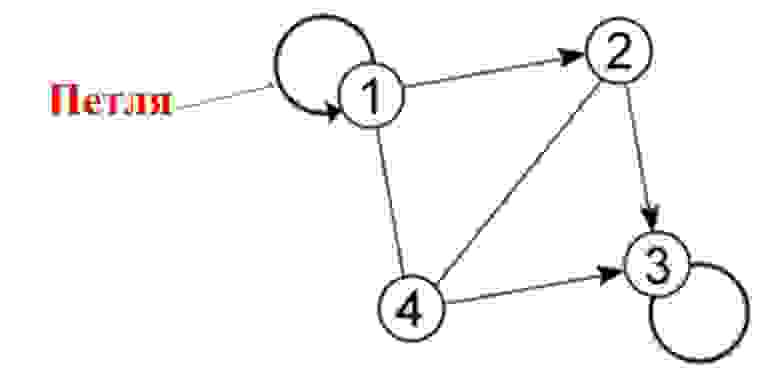
В ориентированном графе все немного по-другому (Рисунок 2), так у нас имеется направление, которое мы не в силах поменять. Если вершина 1 смежна вершине 2, то вершина 2 не может быть смежна вершине 1. То же самое касается и инцидентности. Вершины 1 и 2 инцидентны ребру 12, наоборот не работает.

Рисунок 2

Петли

Петля – это ребро инцидентное одной и той же вершине. То есть вершина которая соединена сама с собой. На рисунке ниже мы видим, как это выглядит.

Петли

Заключение

В следующей статье я покажу, как с помощью матрицы задавать графы, а также покажу, что такое вес ребра.

Источник

Ключевые термины

Дата добавления: 2015-06-12 ; просмотров: 7179 ; Нарушение авторских прав

Вес (длина) ребра – это число или несколько чисел, которые интерпретируются по отношению к ребру как длина, пропускная способность.

Вес вершины – это число (действительное, целое или рациональное), поставленное в соответствие данной вершине.

Взвешенный граф – это граф, каждому ребру которого поставлен в соответствие его вес.

Граф – это совокупность двух конечных множеств: множества точек и множества линий, попарно соединяющих некоторые из этих точек.

Вершины (узлы) графа – это множество точек, составляющих граф.

Замкнутый маршрут – это маршрут в графе, у которого начальная и конечная вершины совпадают.

Кратные ребра – это ребра, соединяющие одну и ту же пару вершин.

Маршрут в графе – это конечная чередующаяся последовательность смежных вершин и ребер, соединяющих эти вершины.

Матрица инцидентности – это двумерный массив, в котором указываются связи между инцидентными элементами графа (ребро и вершина).

Матрица смежности – это двумерный массив, значения элементов которого характеризуются смежностью вершин графа

Мультиграф – это граф, у которого любые две вершины соединены более чем одним ребром.

Неориентированный граф (неорграф) – это граф, у которого все ребра неориентированы, то есть ребрам которого не задано направление.

Обход графа (поиск на графе) – это процесс систематического просмотра всех ребер или вершин графа с целью отыскания ребер или вершин, удовлетворяющих некоторому условию.

Ориентированный граф (орграф) – это граф, у которого все ребра ориентированы, то есть ребрам которого присвоено направление.

Открытый маршрут – это маршрут в графе, у которого начальная и конечная вершины различны.

Петля – это ребро, соединяющее вершину саму с собой.

Поиск в глубину – это обход графа по возможным путям, когда нужно сначала полностью исследовать одну ветку и только потом переходить к другим веткам (если они останутся нерассмотренными).

Поиск в ширину – это обход графа по возможным путям, когда после посещения вершины, посещаются все соседние с ней вершины.

Простой граф – это граф, в котором нет ни петель, ни кратных ребер.

Путь – это открытая цепь, у которой все вершины различны.

Ребра (дуги) графа – это множество линий, соединяющих вершины графа.

Связный граф – это граф, у которого для любой пары вершин существует соединяющий их путь.

Смежные вершины – это вершины, соединенные общим ребром.

Смешанный граф – это граф, содержащий как ориентированные, так и неориентированные ребра.

Список ребер – это множество, образованное парами смежных вершин

Тупик – это вершина графа, для которой все смежные с ней вершины уже посещены

Цепь – это маршрут в графе, у которого все ребра различны.

Цикл – это замкнутая цепь, у которой различны все ее вершины, за исключением концевых.

Источник

Основные понятия и определения

Дата добавления: 2015-07-23 ; просмотров: 1166 ; Нарушение авторских прав

Чтобы составить наглядное представление о графе, достаточно вообразить некоторое множество точек плоскости или пространства и множество отрезков, соединяющих все или некоторые из этих точек.

Граф, образованный ребрами называют неориентированными (рис. 1).

Граф, состоящий из дуг, называют ориентированными (орграфом)(рис.2).

Рассматриваются и смешанные графы – графы, состоящие из ребер и дуг ( рис. 3 ).

Рис. 3. Смешанный граф.

Формально граф G определяется заданием двух множеств X и U, где X – множество вершин, U – множество дуг ( ребер ), т.е. G = ( X, U ).

Для неориентированного графа ( рис. 1 ) множество вершин X и ребер U можно записать так

Для ориентированного графа ( рис. 2 ) множества вершин и дуг записываются следующим образом

или

.

Ребро, начало и конец которого совпадают, называется петлей ( рис.4 ).

Рис. 4. Несвязный неориентированный граф

Вершины называются смежными, или соседними, если существует ребро, их соединяющее

.

Вершины несмежные ( рис. 4 ).

Два ребра называются смежными, если они имеют общую вершину, например, ребра имеют общую вершину ( рис. 1 ).

Ребро называется инцидентным вершине , если оно выходит или входит в вершину.

Степенью вершины называют число инцидентных ей ребер ( дуг ). Степень вершины обозначают: . Например ( рис. 4 ), , поскольку ребро учитывается дважды.

Вершина, степень которой равна нулю, называется изолированной, например .

Вершина, степень которой равна единице, называется висячей или тупиковой, .

Теорема 1.В графе G = ( X, U ) сумма степеней всех его вершин – число четное, равное удвоенному числу ребер графа, т.е.

,

где n = — число вершин, m = — число ребер графа.

Вершина называется четной ( нечетной ), если ее степень четное ( нечетное ) число.

Теорема 2.Число нечетных вершин любого графа – четно.

Кратностьюпары вершинназывается число соединяющих их ребер или дуг. Например, на рис. 5 ребро имеет кратность равную 3, а ребро — красность, равную 2.

Дугиорграфа называются кратными, если они имеют одинаковые начальные и конечные вершины, т.е. одинаковые направления. Например, на рис. 6 кратны дуги

.

Маршрутом называют последовательность вершин и ребер, в которой конец предыдущего ребра совпадает с началом следующего. Число ребер в маршруте определяет его длину.

Например, —маршрут, длина которого равна 6 ( рис. 4 ).

Цепью называется маршрут, в котором все ребра попарно различны. Например, —цепь, длина которой равна 4 ( рис. 4 ).

Простой называется цепь, в которой все вершины попарно различны. Например, ( рис. 4 ).

Граф называется связным, если для любых двух его вершин существует цепь, соединяющая эти вершины ( рис. 7 ) и несвязными, если есть хотя бы одна вершина, для которой такой цепи нет ( рис. 4, вершина ).

Рис. 7. Связный граф

Расстоянием между вершинами связного графа называется длина самой короткой цепи, соединяющей вершины.

Диаметромграфа называется максимальное расстояние между его вершинами.

Циклом( простым циклом ) называется цепь ( простая цепь ) начало и коней которой совпадают. Например, последовательность образует цикл ( рис. 4 ).

Подграфомграфа G называется граф с множеством вершин и множеством ребер , такой, что . Например, для графа ( рис. 4 ) подграфом может быть

где = ,а

= .

Подграф называется собственным, если он отличен от самого графа.

Компонентов связности графа называется его связный подграф, не являющийся собственным подграфом никакого другого связного подграфа данного графа. Например, граф G ( рис.4 ) имеет две компоненты связности.

Точкой сочленения называется вершина графа, удаление которой повышает число компонент связности. Под удалением вершины понимается удаление самой вершины и всех инцидентных ей ребер.Например, точкой сочленения является вершина ( рис. 4 ), удаление которой приводит к появлению третьей компоненты связности.

Граф G называется полным, если любые две его вершины соединены ребром ( рис. 7 ). Таким образом, полный граф определяется только своими вершинами.

Пусть число вершин полного графа равно n. Тогда степень любой вершины равны ,а число ребер равно числу сочетаний из n по 2, т.е.

Число ребер, согласно теореме 1, равно

Теорема 3.Для того чтобы связный граф G являлся простым циклом, необходимо и достаточно, чтобы каждая его вершина имела степень, равную 2.

Ребро связного графа G называется мостом, если после его удаления G станет несвязным и распадается на два связных графа . Например, для связного графа мостами являются ребра и ( рис. 8 ).

Теорема 4.Ребро графа является мостом тогда и только тогда, когда не принадлежит ни одному циклу.

Рис. 9. Изоморфизм графов

словами графы называются изоморфными, если существует взаимно – однозначное соответствие между их ребрами и вершинами, причем соответствующие ребра соединяют соответствующие вершины.

Источник