Что такое неупругое соударение
Что такое упругий и неупругий удар
Задачи физики, в которых рассматриваются движущиеся и ударяющиеся друг о друга тела, предполагают для их решения знание законов сохранения импульса и энергии, а также понимание специфики самого взаимодействия. В данной статье дается теоретическая информация об упругом и неупругом ударах. Также приводятся частные случаи решения задач, связанных с данными физическими понятиями.
Количество движения
Перед рассмотрением абсолютно упругого и неупругого удара необходимо дать определение величине, которая известна, как количество движения. Ее принято обозначать латинской буквой p. Вводится в физику она просто: это произведение массы на линейную скорость движения тела, то есть имеет место формула:
Вам будет интересно: Алебастр: формула и виды
Это векторная величина, но для простоты она записана в скалярной форме. В данном понимании количество движения рассматривалось Галилеем и Ньютоном в XVII веке.
Эта величина не выводится. Ее появление в физике связано с интуитивным пониманием наблюдаемых в природе процессов. Например, каждый хорошо представляет, что остановить лошадь, которая бежит со скоростью 40 км/ч, гораздо тяжелее, чем муху, летящую с той же скоростью.
Импульс силы
Вам будет интересно: Арифметический квадратный корень и его свойства
Количество движения многие называют просто импульсом. Это не совсем верно, поскольку под последним понимают воздействие силы на объект в течение некоторого промежутка времени.
Если сила (F) не зависит от времени ее действия (t), тогда импульс силы (P) в классической механике записывается следующей формулой:
Пользуясь законом Ньютона, перепишем это выражение так:
Мы получили интересный результат: импульс силы равен количеству движения, которое он сообщает телу. Именно поэтому многие физики просто опускают слово «сила» и говорят импульс, имея в виду количество движения.
Записанные формулы также ведут к одному важному выводу: при отсутствии внешних сил любые внутренние взаимодействия в системе сохраняют ее суммарное количество движения (импульс силы равен нулю). Последняя формулировка известна в качестве закона сохранения импульса изолированной системы тел.
Понятие о механическом ударе в физике
Вам будет интересно: Что свидетельствует о зарождении феодальных отношений на Руси?
Теперь пришло время перейти к рассмотрению абсолютно упругого и неупругого ударов. Под механическим ударом в физике понимают одновременное взаимодействие двух или более твердых тел, в результате которого происходит обмен энергией и количеством движения между ними.
Частными случаями столкновения являются абсолютный упругий и неупругий удары (последний также называют эластичным или пластичным). Рассмотрим, что они собой представляют.
Идеальные виды ударов
Упругие и неупругие удары тел являются идеализированными случаями. Первый из них (упругий) означает, что при столкновении двух тел не создается никакой остаточной деформации. Когда одно тело сталкивается с другим, то в некоторый момент времени происходит деформация обоих объектов в области их контакта. Эта деформация служит механизмом передачи энергии (количества движения) между объектами. Если она является абсолютно упругой, то после удара никаких потерь энергии не происходит. В этом случае говорят о сохранении кинетической энергии взаимодействующих тел.
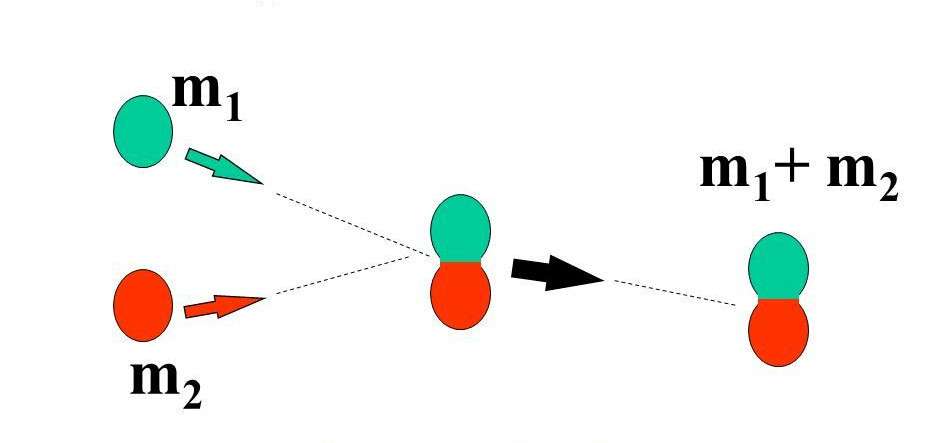
Второй вид ударов (пластический или абсолютно неупругий) означает, что после соударения одного тела о другое, они «слипаются» друг с другом, поэтому после удара оба объекта начинают двигаться как единое целое. В результате этого удара некоторая часть кинетической энергии расходуется на деформацию тел, трение, выделение тепла. При этом виде соударения энергия не сохраняется, но количество движения остается неизменным.
Абсолютно упругое столкновение
m1*v1 +m2*v2 = m1*u1 +m2*u2.
Эта система используется для решения любых задач с любыми начальными условиями. В данном примере ограничимся частным случаем: пусть массы m1 и m2 двух шаров равны. Кроме того, начальная скорость второго шара v2 равна нулю. Необходимо определить результат центрального упругого столкновения рассматриваемых тел.
С учетом условия задачи, перепишем систему:
Подставляем второе выражение в первое, получаем:
u12 + u22 + 2*u1*u2 = u12 + u22 => u1*u2 = 0
Последнее равенство справедливо, если одна из скоростей u1 или u2 равна нулю. Вторая из них не может быть нулевой, поскольку при попадании первого шара во второй, он неминуемо начнет двигаться. Это означает, что u1 = 0, а u2 > 0.
Таким образом при упругом столкновении движущегося шара с покоящимся, массы которых одинаковы, первый передает свой импульс и энергию второму.
Неупругий удар
В этом случае шар, который катится, при столкновении со вторым шаром, который покоится, прилипает к нему. Дальше оба тела начинают движение, как одно целое. Поскольку импульс упругих и неупругих ударов сохраняется, то можно записать уравнение:
m1*v1 + m2*v2 = (m1 + m2)*u
Поскольку в нашей задаче v2=0, то конечная скорость системы из двух шаров определиться следующим выражением:
В случае равенства масс тел, получаем еще более простое выражение:
Скорость двух слипшихся шаров будет в два раза меньше, чем эта величина для одного шара до момента столкновения.
Коэффициент восстановления
m1*v12 + m2*v22 = m1*u12 + m2*u22;
m1*v1 + m2*v2 = m1*u1 + m2*u2.
После ряда упрощений можно получить формулу:
Ее в виде отношения разности скоростей можно переписать следующим образом:
Коэффициент восстановления K имеет вид:
Расчет коэффициента восстановления для «прыгающего» тела
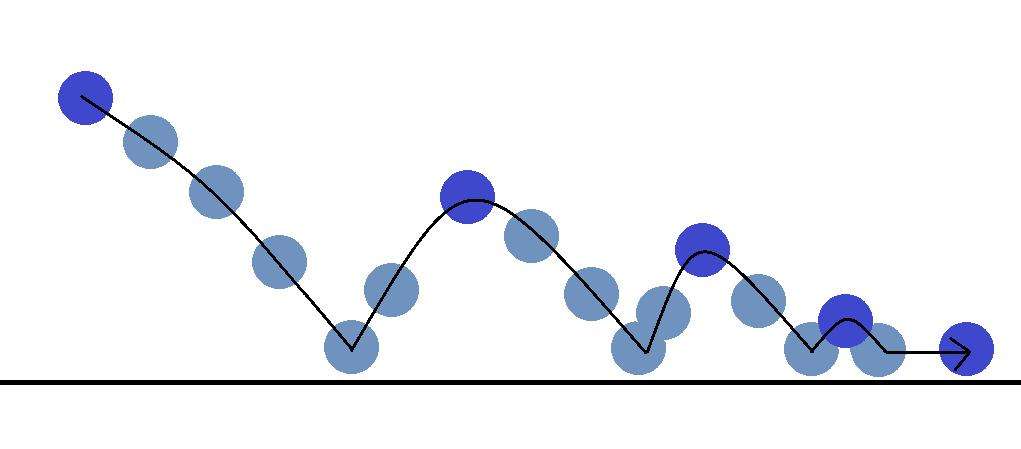
В зависимости от характера удара, коэффициент K может существенно отличаться. Рассмотрим, как можно его рассчитать, для случая «прыгающего» тела, например, футбольного мяча.
Сначала мяч держат на некоторой высоте h0 над поверхностью земли. Затем его отпускают. Он падает на поверхность, отскакивает от нее и поднимается на некоторую высоту h, которую фиксируют. Поскольку скорость поверхности земли до и после ее соударения с мячом была равна нулю, то формула для коэффициента будет иметь вид:
Здесь v2=0 и u2=0. Знак минус исчез, потому что скорости v1 и u1 направлены противоположно. Поскольку падение и подъем мяча является движением равноускоренным и равнозамедленным, то для него справедлива формула:
Выражая скорость, подставляя значения начальной высоты и после отскока мяча в формулу для коэффициента K, получим конечное выражение: K = √(h/h0).
21.1 Конспект для учителя по теме «Абсолютно упругий и неупругий удары. Законы сохранения при соударениях»
Для изучения строения вещества, так или иначе, используются различные столкновения. Например, для того, чтобы рассмотреть какой-то предмет, его облучают светом, или потоком электронов, и по рассеянию этого света, или потока электронов получают фотографию, или рентгеновский снимок, или изображение данного предмета в каком-либо физическом приборе. Таким образом, столкновение частиц – это то, что окружает нас и в быту, и в науке, и в технике, и в природе.
Например, при одном столкновении ядер свинца в детекторе ALICE Большого Адронного Коллайдера рождаются десятки тысяч частиц, по движению и распределению которых можно узнать о самых глубинных свойствах вещества. Рассмотрение процессов столкновения с помощью законов сохранения, о которых мы говорим, позволяет получать результаты, независимо от того, что происходит в момент столкновения. Мы не знаем, что происходит в момент столкновения двух ядер свинца, но мы знаем, какова будет энергия и импульс частиц, которые разлетаются после этих столкновений.
В статье мы рассмотрим взаимодействие тел в процессе столкновения, иными словами движение невзаимодействующих тел, которые меняют свое состояние только при соприкосновении, которое мы называем столкновением, или ударом.
При столкновении тел, в общем случае, кинетическая энергия сталкивающихся тел не обязана быть равной кинетической энергии разлетающихся тел. Действительно, при столкновении тела взаимодействуют друг с другом, воздействуя друг на друга и совершая работу. Эта работа и может привести к изменению кинетической энергии каждого из тел. Кроме того, работа, которую совершает первое тело над вторым, может оказаться неравной работе, которую второе тело совершает над первым. Это может привести к тому, что механическая энергия может перейти в тепло, электромагнитное излучение, или даже породить новые частицы.
Не упрогий удар
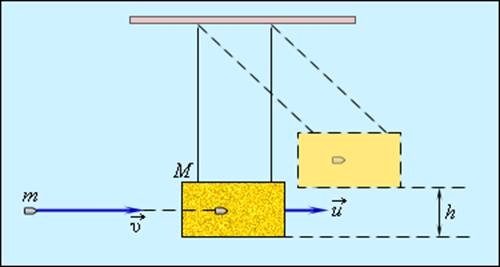
Рис. 1. Абсолютное неупругое столкновение
Условие, что пуля застряла в ящике, и есть признак абсолютно неупругого удара. Проверим, что произошло с кинетической энергией в результате этого удара. Начальная кинетическая энергия пули:
конечная кинетическая энергия пули и ящика:
простая алгебра показывает нам, что в процессе удара кинетическая энергия изменилась:
Итак, начальная кинетическая энергия пули меньше конечной на некоторую положительную величину. Как же это произошло? В процессе удара между песком и пулей действовали силы сопротивления. Разность кинетических энергий пули до и после столкновения как раз и равны работе сил сопротивления. Другими словами, кинетическая энергия пули пошла на нагрев пули и песка.
Для изучения строения вещества, так или иначе, используются различные столкновения. Например, для того, чтобы рассмотреть какой-то предмет, его облучают светом, или потоком электронов, и по рассеянию этого света, или потока электронов получают фотографию, или рентгеновский снимок, или изображение данного предмета в каком-либо физическом приборе. Таким образом, столкновение частиц – это то, что окружает нас и в быту, и в науке, и в технике, и в природе.
Например, при одном столкновении ядер свинца в детекторе ALICE Большого Адронного Коллайдера рождаются десятки тысяч частиц, по движению и распределению которых можно узнать о самых глубинных свойствах вещества. Рассмотрение процессов столкновения с помощью законов сохранения, о которых мы говорим, позволяет получать результаты, независимо от того, что происходит в момент столкновения. Мы не знаем, что происходит в момент столкновения двух ядер свинца, но мы знаем, какова будет энергия и импульс частиц, которые разлетаются после этих столкновений.
В статье мы рассмотрим взаимодействие тел в процессе столкновения, иными словами движение невзаимодействующих тел, которые меняют свое состояние только при соприкосновении, которое мы называем столкновением, или ударом.
При столкновении тел, в общем случае, кинетическая энергия сталкивающихся тел не обязана быть равной кинетической энергии разлетающихся тел. Действительно, при столкновении тела взаимодействуют друг с другом, воздействуя друг на друга и совершая работу. Эта работа и может привести к изменению кинетической энергии каждого из тел. Кроме того, работа, которую совершает первое тело над вторым, может оказаться неравной работе, которую второе тело совершает над первым. Это может привести к тому, что механическая энергия может перейти в тепло, электромагнитное излучение, или даже породить новые частицы.
Абсолютно упругий удар
Примером абсолютно упругих ударов могут быть столкновения бильярдных шаров. Мы рассмотрим простейший случай такого столкновения – центральное столкновение.
Центральным называется столкновение, при котором скорость одного шара проходит через центр масс другого шара. (Рис. 2.)
Закон сохранения импульса выполняется при любом столкновении шаров:
В случае абсолютно упругого удара, также выполняется закон сохранения энергии:
Получаем систему из двух уравнений с двумя неизвестными величинами. Решив ее, мы получим ответ.
Скорость первого шара после удара равна
заметим, что эта скорость может быть как положительной, так и отрицательной, в зависимости от того, масса какого из шаров больше. Кроме того, можно выделить случай, когда шары одинаковые. В этом случае после удара первый шар остановится. Скорость второго шара, как мы ранее отметили, получилась положительной при любом соотношении масс шаров:
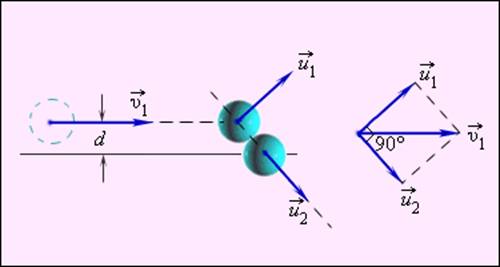
Наконец, рассмотрим случай нецентрального удара в упрощенном виде – когда массы шаров равны. Тогда, из закона сохранения импульса мы можем записать:
А из того, что кинетическая энергия сохраняется:
Таким образом, при абсолютно упругом нецентральном ударе, когда массы шаров равны, они всегда разлетаются под прямым углом друг к другу.
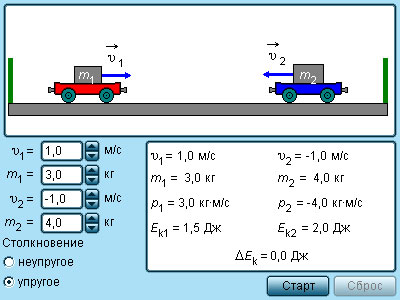
Упругие и неупругие соударения
Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда действующие силы неизвестны. Примером такого рода задач является ударное взаимодействие тел.
С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц).
Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).
Примером абсолютно неупругого удара может служить попадание пули (или снаряда) в баллистический маятник. Маятник представляет собой ящик с песком массой M, подвешенный на веревках (рис. 1.21.1). Пуля массой m, летящая горизонтально со скоростью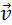 
попадает в ящик и застревает в нем. По отклонению маятника можно определить скорость пули.
Обозначим скорость ящика с застрявшей в нем пулей через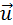 
Тогда по закону сохранения импульса
При застревании пули в песке произошла потеря механической энергии:
Отношение M / (M + m) – доля кинетической энергии пули, перешедшая во внутреннюю энергию системы:
Эта формула применима не только к баллистическому маятнику, но и к любому неупругому соударению двух тел с разными массами.
При m > М) отношение
Дальнейшее движение маятника можно рассчитать с помощью закона сохранения механической энергии:
где h – максимальная высота подъема маятника. Из этих соотношений следует:
Измеряя на опыте высоту h подъема маятника, можно определить скорость пули υ.
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.
Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.
При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.
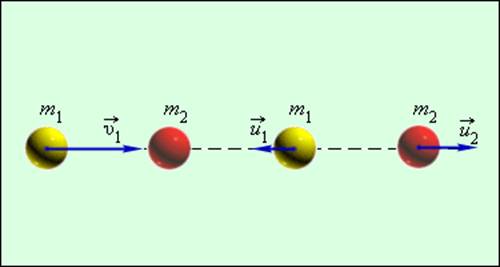
Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя (рис. 1.21.2).
Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.
В общем случае массы m1 и m2 соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии
Здесь υ1 – скорость первого шара до столкновения, скорость второго шара υ2 = 0, u1 и u2 – скорости шаров после столкновения. Закон сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, записывается в виде:
Мы получили систему из двух уравнений. Эту систему можно решить и найти неизвестные скорости u1 и u2 шаров после столкновения:
В частном случае, когда оба шара имеют одинаковые массы (m1 = m2), первый шар после соударения останавливается (u1 = 0), а второй движется со скоростью u2 = υ1, т. е. шары обмениваются скоростями (и, следовательно, импульсами).
Если бы до соударения второй шар также имел ненулевую скорость (υ2 ≠ 0), то эту задачу можно было бы легко свести к предыдущей с помощью перехода в новую систему отсчета, которая движется равномерно и прямолинейно со скоростью υ2 относительно «неподвижной» системы. В этой системе второй шар до соударения покоится, а первый по закону сложения скоростей имеет скорость υ1‘ = υ1 – υ2. Определив по приведенным выше формулам скорости u1 и u2 шаров после соударения в новой системе, нужно сделать обратный переход к «неподвижной» системе.
Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения.
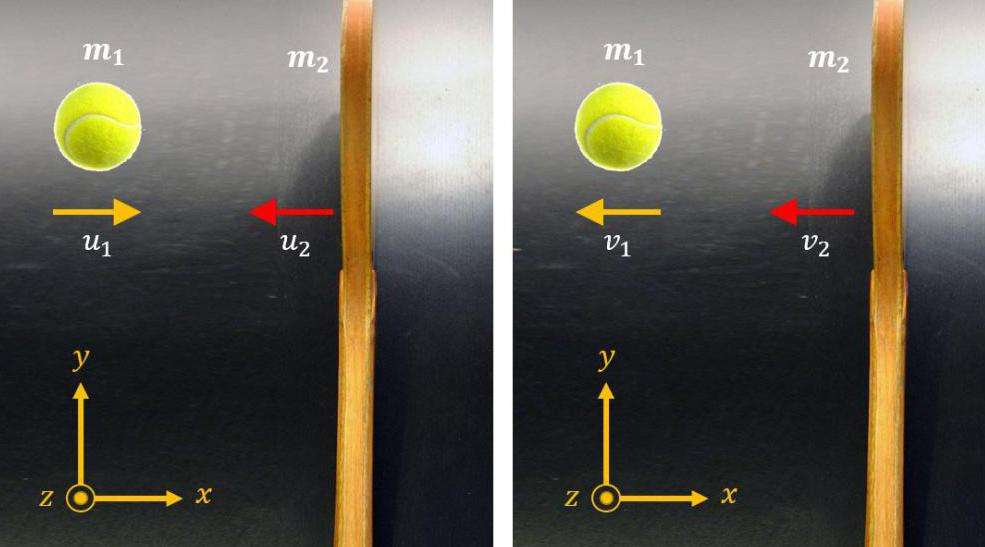
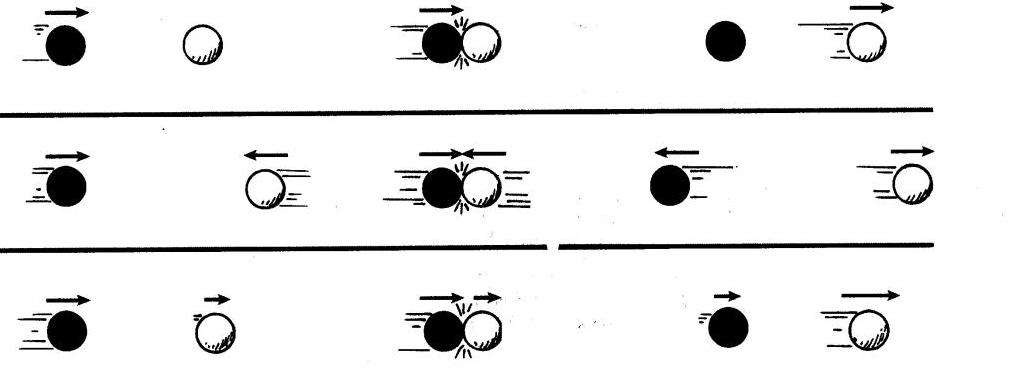
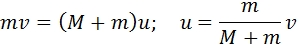
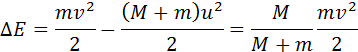
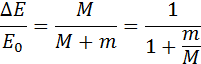
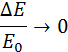
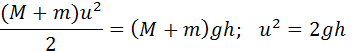
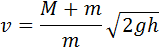
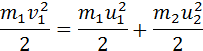
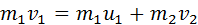
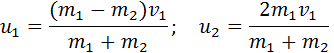
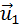и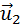 
после удара нужно знать положение линии центров в момент удара или прицельное расстояние d (рис. 1.21.3), т. е. расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости 
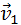налетающего шара. Если массы шаров одинаковы, то векторы скоростей 