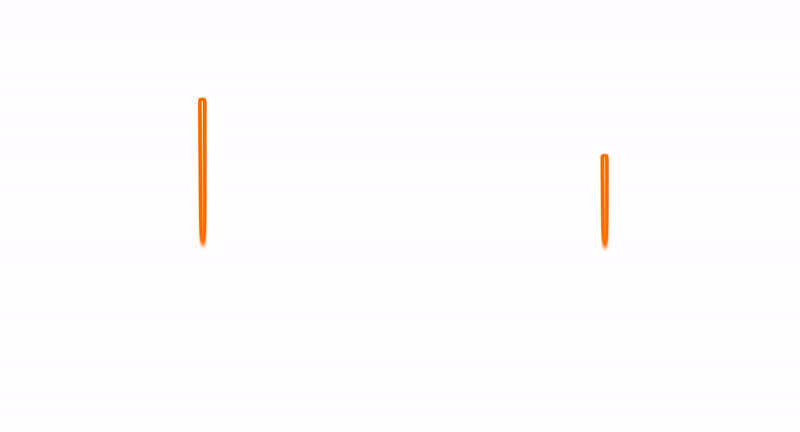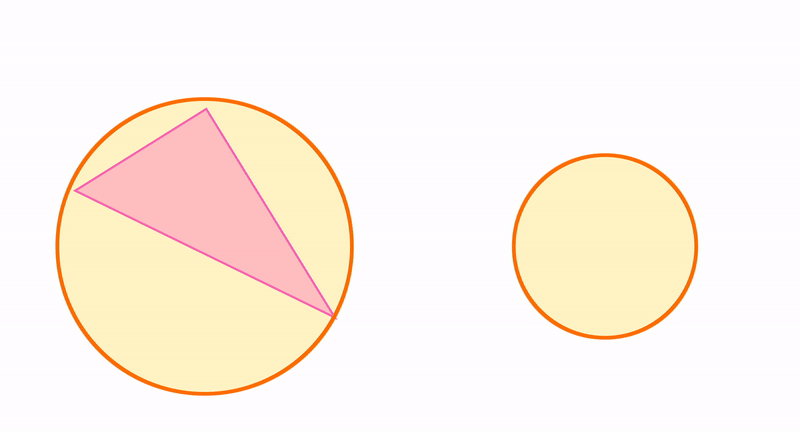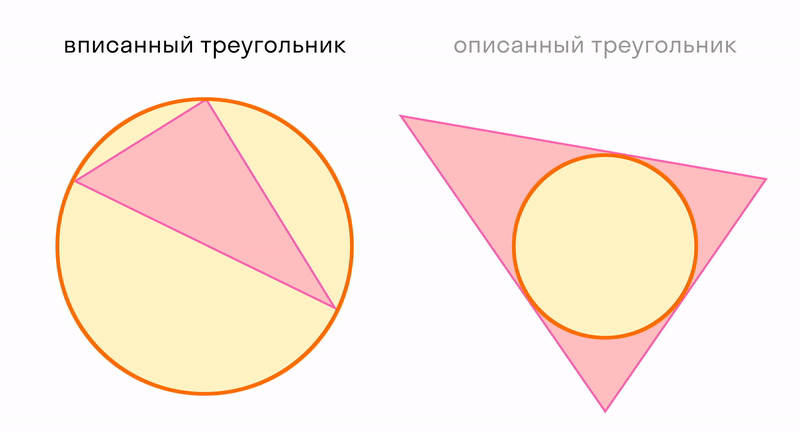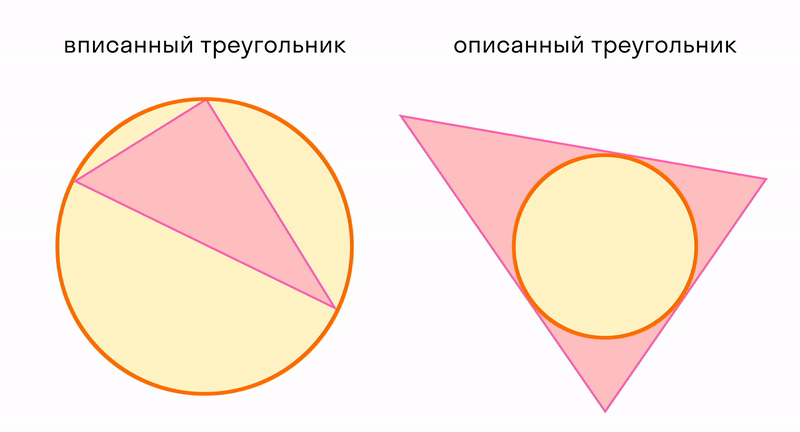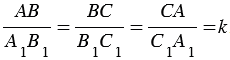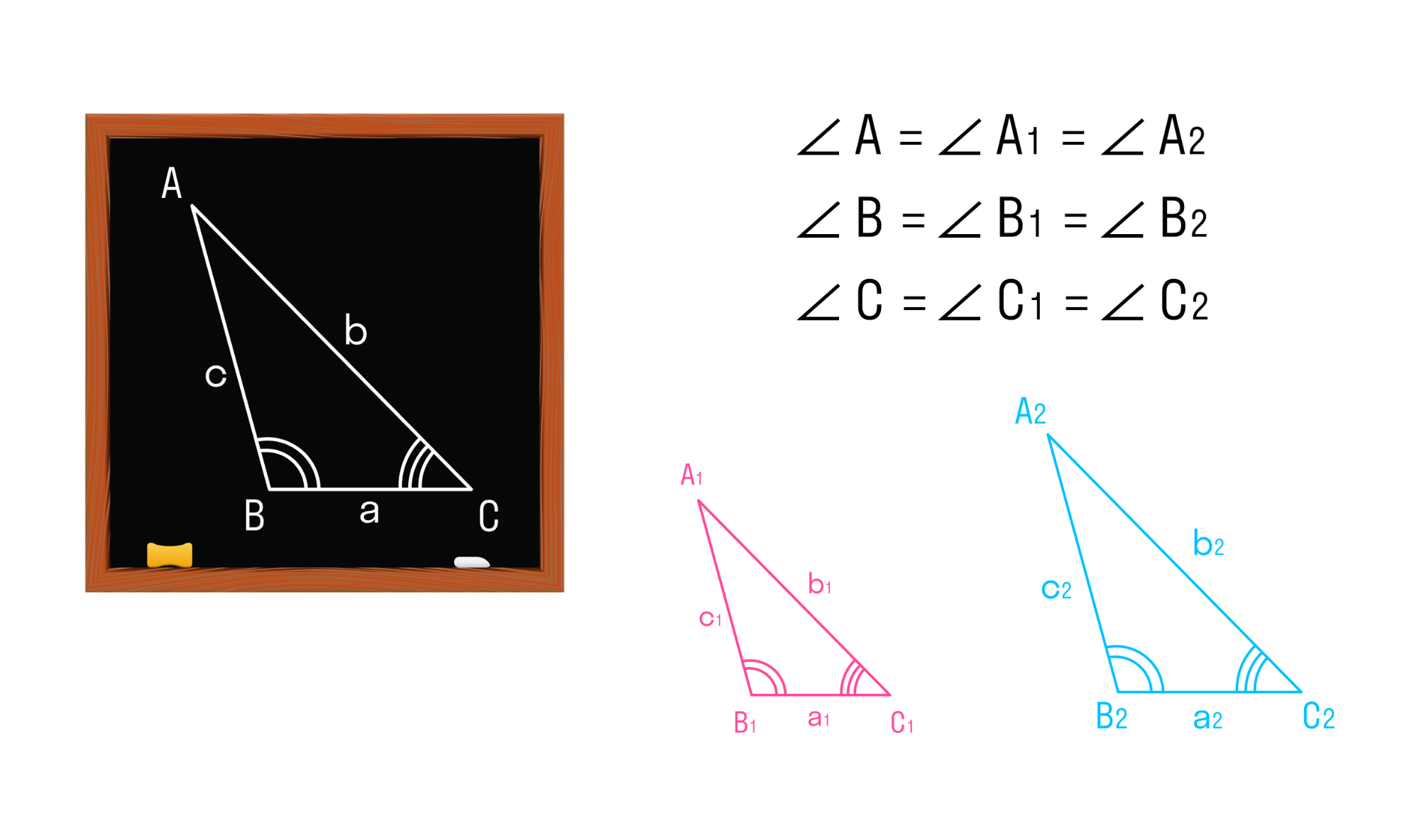Что такое нлу геометрия
Что такое геометрия? Наука геометрия
Геометрия является важной частью математики, которую начинают изучать в школах с 7 класса в качестве отдельного предмета. Что такое геометрия? Что она изучает? Какие полезные выводы можно из нее извлечь? Все эти вопросы подробно рассматриваются в статье.
Понятие о геометрии

В ходе своего развития геометрия обзавелась набором понятий, которыми она оперирует с целью решения различных задач. К таким понятиям относятся точка, прямая, плоскость, поверхность, отрезок, окружность, кривая, угол и другие. Основой этой науки являются аксиомы, то есть концепции, связывающие геометрические понятия в рамках утверждений, которые принимаются в качестве истинных. На основании аксиом строятся и доказываются теоремы.
Когда появилась эта наука

Что такое геометрия с точки зрения истории? Здесь следует сказать, что она является очень древним учением. Так, ее использовали древние вавилоняне при определении периметров и площадей простых фигур (прямоугольников, трапеций и др.). Развита она была и в Древнем Египте. Достаточно вспомнить знаменитые пирамиды, строительство которых было бы невозможно без знания свойств объемных фигур, а также без умения ориентироваться на местности. Отметим, что знаменитое число «пи» (его приблизительное значение), без которого невозможно определить параметры круга, было известно египетским жрецам.
Разрозненные знания о свойствах плоских и объемных тел были собраны в единую науку только во времена Античной Греции благодаря деятельности ее философов. Самым важным трудом, на котором основываются современные геометрические учения, являются «Элементы» Евклида, которые были им составлены приблизительно в 300 году до нашей эры. Около 2000 лет этот трактат являлся основой для каждого ученого, который занимался исследованием пространственных свойств тел.
В XVIII веке французский математик и философ Рене Декарт заложил основы так называемой аналитической науки геометрии, которая описывала с помощью численных функций любой пространственный элемент (прямую, плоскость и так далее). С этого времени начинают появляться многие ветви в геометрии, причиной существования которых является пятый постулат в «Элементах» Евклида.
Евклидова геометрия
Что такое геометрия Евклида? Это достаточно стройное учение о пространственных свойствах идеальных объектов (точек, прямых, плоскостей и т.д.), которое основывается на 5 постулатах или аксиомах, изложенных в труде под названием «Элементы». Аксиомы приведены ниже:
Евклидова геометрия составляет основу любого современного школьного курса по этой науке. Более того, именно ею человечество пользуется в ходе своей жизнедеятельности при конструировании зданий и сооружений и при составлении топографических карт. Здесь важно отметить, что набор постулатов в «Элементах» не является полным. Он был расширен немецким математиком Давидом Гильбертом в начале XX века.
Виды евклидовой геометрии
Мы разобрались, что такое геометрия. Рассмотрим, какие ее виды бывают. В рамках классического учения принято выделять два вида этой математической науки:
Неевклидовы геометрии
Что такое геометрия в ее широком понимании? Помимо привычной нам науки о пространственных свойствах тел, существуют также неевклидовы геометрии, в которых пятый постулат в «Элементах» нарушается. К ним относятся эллиптическая и гиперболическая геометрии, которые были созданы в XIX веке немецким математиком Георгом Риманом и русским ученым Николаем Лобачевским.
Изначально полагали, что неевклидовы геометрии имеют узкую область применения (например, в астрономии при изучении небесной сферы), а само физическое пространство является евклидовым. Ошибочность последнего утверждения показал Альберт Эйнштейн в начале XX века, разработав свою теорию относительности, в которой он обобщил понятия пространства и времени.
Геометрия в школе
Как было сказано выше, изучение в школе геометрии начинается с 7 класса. При этом школьникам демонстрируют основы планиметрии. Геометрия 9 класса уже включает изучение трехмерных тел, то есть стереометрию.
Главная задача школьного курса состоит в том, чтобы развить у школьников абстрактное мышление и воображение, а также научить их мыслить логически.
Многие исследования показали, что при изучении этой науки у школьников наблюдаются проблемы с абстрактным мышлением. Когда формулируется для них геометрическая задача, они часто не понимают ее суть. У старшеклассников к проблеме с воображением добавляются трудности понимания математических формул для определения объема и площади поверхности разверстки пространственных фигур. Часто старшеклассники при изучении геометрии 9 класса не знают, какой формулой следует воспользоваться в конкретном случае.
Школьные учебники
Существует большое количество учебных пособий для обучения школьников этой науке. Одни из них дают только базовые знания, например, учебники Л. С. Атанасяна или А. В. Погорелова. Другие преследуют цель углубленного изучения науки. Здесь можно выделить учебник А. Д. Александрова или полный курс геометрии Бевза Г. П.
Поскольку в последние годы для сдачи всех экзаменов в школе введен единый стандарт ЕГЭ, стали необходимы учебники и решебники, которые позволяют ученику быстро самостоятельно разобраться с необходимой темой. Хорошим примером таких пособий можно назвать геометрию Ершовой А. П., Голобородько В. В.
Любой из названных выше учебников имеет как положительные, так и отрицательные отзывы со стороны учителей, поэтому преподавание в школе геометрии часто осуществляется с использованием нескольких учебников.
Что такое NLU и как его применить
Другими словами это сервис позволяющий понимать и разбирать основные смыслы из диалогов с клиентом. Чаще всего NLU используется для создания голосовых роботов и чат ботов.
В самом упрощённом виде, процесс «понимания» языка состоит из следующих крупных этапов:
-Предварительная обработка текста (запроса)
-Классификация запроса, соотнесение с одним из классов, известных системе (определение намерения)
-Извлечение параметров запроса (извлечение сущностей)
Основные термины в NLU
Естественный язык – это язык, который используется группами людей для передачи информации друг другу, для общения. Естественным он называется, потому что образовался и развивается естественным путём, то есть его не создавала группа людей целенаправленно. Например, русский язык, английский, немецкий, французский, испанский и далее.
Модель – это несколько нейронных сетей и набор правил, характерные для конкретной проблемы/предметной области/сценария/вида диалогов. Модель включает данные для обучения, конкретный набор правил и обученные нейронные сети.
Сущность – это конкретный параметр текста, какая-либо точная информация из него, например дата, время, место, адрес, ФИО, числа, денежные единицы, расстояние, продолжительность, номера телефонов, количество чего-либо, температура, объём, url адреса.
Намерение – это то, что хочет пользователь, его замысел, что он хочет получить от бота, какая цель его обращения, в чём его суть и смысл.
Агент – это обученная и пригодная для использования модель NLU.
Как устроен NLU?
В leadozvon NLU состоит из 5 частей
1. Подготовка текста, она включает:
Лемматизация – приведение каждого слова в каждом обучающем примере к его начальной/словарной форме (т.е. к форме, в которой слово пишется в словаре).
Стемминг – удаление в каждом слове в каждом обучающем примере окончаний и некоторых простых суффиксов (т.е. от каждого слова остаётся только его основа).
Лемматизация со стеммингом – сначала выполняется лемматизация, а затем стемминг.
Удаление всех символов, кроме букв русского и английского алфавита, знаков препинания и цифр (данная операция зависит от языка, с которым работает NLU).
2. Перевод текста в последовательность чисел – так как любые компьютеры могут работать только с числами, текст в начале необходимо перевести в набор чисел по определённым правилам. За это отвечает «языковая модель».
3. Классификация текста/определение намерения/темы – это соотнесение полученного текста с одним из известных классов/намерений. Это попытка понять, что хочет пользователь, какое у него намерение, что он хочет получить от бота, какая цель его обращения, в чём его суть и смысл.
4. Извлечение стандартных (базовых) сущностей – это извлечение базовых параметров текста, таких как: дата, время, место, адрес, ФИО, числа, денежные единицы, расстояние, продолжительность, номера телефонов, количество чего-либо, температура, объём, url адреса.
5. Извлечение специфичных/пользовательских сущностей – это извлечение специфичных для конкретного варианта использования параметров текста (например, вес и размеры посылки, название товара или услуги, вид транспорта, вид деятельности).
Результат работы NLU
Результатом работы NLU является классифицированное намерение и набор сущностей, которые удалось извлечь. Затем эти значения отправляются в «ядро» бота, где уже на их основании и с помощью конкретного сценария выбирается ответная реакция бота.
Следует помнить, что NLU в любом случае, вне зависимости от присланного текста и каких-либо параметров, пытается соотнести его с каждым намерением, которое он знает. А в ответе он выводит список из всех намерений и вероятность принадлежности присланного текста к каждому намерению.
Как работает NLU и как его обучать?
Большую часть NLU составляют искусственные нейронные сети. То есть NLU работает по тем же принципам, что и используемые в нём нейронные сети.
Для понимания работы нейронных сетей можно применить аналогию с обучением ребёнка. Изначально у нейронной сети, как и у ребёнка, нет никакого понимания того, что от неё хотят. И мы, с помощью обучающих примеров, должны научить нейронную сеть делать то, что нам нужно, как маленького ребёнка мы учим понимать алфавит, простые распространённые фразы, читать, строить предложения, говорить и т.д.
Это означает, что от качества и количества наших обучающих примеров полностью зависит то, как хорошо NLU будет понимать и уметь делать то, что мы от него хотим.
Максимально чётко разграничивать намерения, что бы вероятность смыслового пересечения между намерениями была минимальной
Подбирать обучающие примеры так, что бы они были максимально приближены к реальным возможным фразам от живых людей
Покрывать обучающими примерами как можно больше различных ситуаций, характеризующих конкретное намерение
Пытаться максимально полно «смоделировать» конкретную проблему/предметную область/сценарий/вид диалога, что бы у NLU было как можно более целостное представление о том, «что он делает»
Прорабатывать и анализировать основные паттерны поведения людей в тех темах/проблемах/сценариях, которым мы хотим обучить NLU
Учитывать, что намерения никак не связаны с «ядром» бота, сценарием и контекстом диалога, в котором они используются. Они всегда должны отражать суть фразы или слова без учёта контекста диалога
В большинстве случаев, качество и точность обученной модели NLU зависит примерно на 60-70% от того, на каких данных она обучалась, и примерно на 30-40% от самого NLU. NLU – это по сути инструмент, который мы обучаем и используем для анализа фраз от людей, их реакций на те или иные события, их поведения, целей и намерений.
Так же большую роль в работе NLU играет языковая модель. Она отвечает за перевод слов в последовательность чисел. От качества этого перевода зависит то, сколько слов будет понимать NLU, будет ли он различать похожие слова, синонимы и антонимы, корректно обрабатывать фразы с ранее неизвестными словами.
Сейчас языковая модель строится следующим образом: все обучающие примеры в каждом намерении разбиваются на слова и словосочетания, затем они объединяются в один общий список и каждому слову и словосочетанию присваивается уникальное число. Этот подход имеет много недостатков и в будущем будет заменён другим, более качественным и точным, который будет содержать несколько миллионов слов и связей между ними.
Однако и на данный момент, и в будущем, особенно важно максимально полно прорабатывать предметную область будущей модели, что бы все компоненты получили целостное представление о том, «что они делают».
Шаг 9. Положение лежа на животе – статический тест.



А. Нижние латеральные углы (НЛУ) крестца (Н)
Оценка НЛУ является частью рутинного скрининга крестцово-подвздошной дисфункции. Если НЛУ симметричны, то дисфункции, вероятно, нет. Редким исключением является наличие двусторонней симметричной дисфункции крестцово-подвздошных суставов. Респираторные функции суставов могут также быть повреждены без какой-либо асимметрии НЛУ.
Обнаружение НЛУ
Нижние латеральные углы (НЛУ) являются крыльями или аналогами поперечных отростков пятого крестцового сегмента (позвонка). Они лежат в той же поперечной плоскости, что и крестцовое отверстие, являющееся нижним проходом в крестцовый канал и находятся чуть латеральнее крестцовых рогов, которые являются аналогами расщепленных остистых отростков в нижнем конце срединного гребня крестца. Заднее смещение одного из НЛУ представляет собой ротацию крестца в эту сторону. Нижнее смещение одного из НЛУ представляет собой боковое сгибание крестца в эту сторону.
Рис. 6.68. Нижние латеральные углы крестца
Крылья S5 (аналоги поперечных отростков пятого крестцового сегмента) называются нижними латеральными углами. Обычно они расположены чуть латеральнее крестцовых рогов, которые являются аналогами расщепленных остистых отростков крыльев S5.
(Из: Mellioni’s Illustrated Medical Dictionary, 3-е издание, 1993, Parthenon Publishing)
Рис. 6.69А. Стереогностическое определение НЛУ.
Поскольку пятый крестцовый сегмент является самой задней частью крестца, стереогностическое распознавание сегмента S5 у лежащего на спине пациента проводится довольно легко. Как только самый задний сегмент крестца определяется пальпацией, мы знаем, что ГЛУ будут находиться по бокам от средней линии крестца, достаточно далеко от рога.
Рис. 6.69Б. Пальпация срединного гребня крестца.
Пальпация срединного гребня крестца одним пальцем, начиная с самой верхней части крестца и сдвигая палец вниз в поисках крестцового отверстия.
Рис. 6.69В. Палец на крестцовом отверстии.
Когда палец находится на отверстии, крестцовый рог обычно чувствуется по сторонам подушечки пальца. У некоторых пациентов отверстие является слишком узким, чтобы соответствовать размеру подушечки пальца, поэтому отверстие чувствуется как еще один остистый отросток срединного гребня. В этом случае более надежным для определения НЛУ является использование метода, показанного на рис. 6.69А.
Есть два метода пальпации для нахождения НЛУ. Один из них – это пальпация подушечкой пальца срединного гребня крестца от верхушки врожденного расщепления до бифуркации, которая образует крестцовые рога. Тогда подушечка пальца ложится на крестцовое отверстие и будет ощущать кость (рога) по сторонам пальца. Каждая из подушечек пальцев врача затем располагается симметрично на плоскости одного поперечного отростка в 1-1,5 см кнаружи от средней линии отверстия, т.е., достаточно далеко, чтобы уйти от рогов, размер и форма которых могут не быть симметричными, но не настолько далеко, чтобы выйти за пределы крестца. Тонкие мягкие ткани, покрывающие НЛУ, затем отжимаются передним надавливанием (чуть менее 0,5 кг) большими пальцами, чтобы ощутить относительную жесткость кости. Опустите голову, чтобы взгляд был почти горизонтальным, и наблюдайте большие пальцы на одностороннее смещение кзади.
Альтернативным методом обнаружения НЛУ является использование стереогностической пальпации. Ладонь кладется на заднюю поверхность крестца для определения наиболее кзади расположенной его части (сегмент S5). Этот метод может оказаться необходимым, если отверстие слишком узко для того, чтобы соответствовать размерам подушечки пальца.
В любом случае, когда НЛУ с одной стороны сдвинут больше назад, то на этой же стороне он будет расположен ниже. Причина этого в том, что каудальная часть поверхности крестцово-подвздошного сустава является широкой колеей, направляющей крестец вниз и назад. Этот факт можно использовать для уточнения результатов пальпаторной и визуальной оценки, потому что единственный путь, которым могут двигаться НЛУ в нижнем направлении – уходить назад, и наоборот. Если вы обнаружили, что НЛУ с одной стороны ниже, но не сзади, один из ваших результатов недостаточно надежен.
Примечание. Всегда сперва подходите к НЛУ сзади, и никогда снизу. Нижние срединные кости – это копчик, первые кости, которые вы встретите при подходе к НЛУ снизу. После оценки задней поверхности НЛУ на ротацию крестца, пальцы соскальзывают с нижних граней крестца, и при необходимости, тянут за собой кожу. Когда подушечки пальцев давят кверху на нижние грани крестца, можно проводить его оценку на боковое сгибание.
Рис. 6.69Г. НЛУ относительно крестцового отверстия.
Избегайте пальпировать рога, поскольку их форма и размеры часто могут быть неодинаковыми. Уйдите достаточно далеко кнаружи от отверстия, чтобы перейти на НЛУ, но не так, чтобы выйти за пределы крестца.
Рис. 6.69Д. Наблюдение переднезадней симметрии НЛУ
Снизьте линию взгляда, чтобы видеть большие пальцы на задних поверхностях НЛУ, соответственно, вы можете наблюдать ротацию крестца. Ротация может давать до сантиметра асимметрии.
Рис. 6.69Е. Пальцы на нижних гранях НЛУ.
Проскользните пальцами вместе с кожей от задней части ГЛУ к нижним граням, поворачивая подушечки пальцев так, чтобы надавливать кверху. Направление взгляда проводящего обследование сдвигается к вертикали для распознавания верхненижней асимметрии НЛУ.
Рис. 6.69Ж. Тест «Сфинкса» для определения скручивания крестца кзади.
Если позвоночник достаточно прогибается назад, асимметрия НЛУ при переднем скручивании крестца исчезает, а асимметрия заднего скручивания ухудшается. Тест «Сфинкс» слабо воздействует на односторонние дисфункции крестцового сгибания.
Шаг 10. Лежа на животе – динамические тесты.
Основы геометрии
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Идеальные объекты
Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.
Основные геометрические объекты: окружность, квадрат, ромб, прямоугольник, равносторонний треугольник, равнобедренный треугольник, правильный многоугольник, эллипс и другие.
Все эти фигуры обладают двумя свойствами:
Равенство частей можно заметить у квадрата, ромба или равностороннего треугольника — равенство сторон. Также у них есть одна или несколько линий симметрии.
У шара бесконечное количество осей симметрии и плоскостей симметрии, но отсутствует равенство или подобие составных частей.
Все типы правильных многогранников обладают симметрией, при этом составлены из некоторого количества одинаковых фигур (треугольников, квадратов, пятиугольников).
Из всего этого можно сделать вывод, что отличить правильную геометрическую фигуру от произвольной совсем не сложно. Достаточно выяснить, имеет ли данная фигура оси или плоскости симметрии, а также из каких повторяющихся частей она состоит.
Таким образом, именно по наличию или отсутствию симметрии и равенства или подобия составных частей можно оценивать различные объекты окружающего мира на соответствие правильному геометрическому виду.
Например, возьмем два треугольника. На первый взгляд, они похожи, но у одного из них одна сторона вогнутая, вторая — выпуклая. А у другого наоборот.
Математика занимается идеальными объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.
Например, теорема Пифагора звучит так: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. А затем это свойство можно применять при решении задач и составлении чертежей.
Базовые геометрические объекты
Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.
Точка — это идеальный математический объект, у которого нет длины и ширины.
Отрезок — это часть прямой, у которого есть начало и конец.
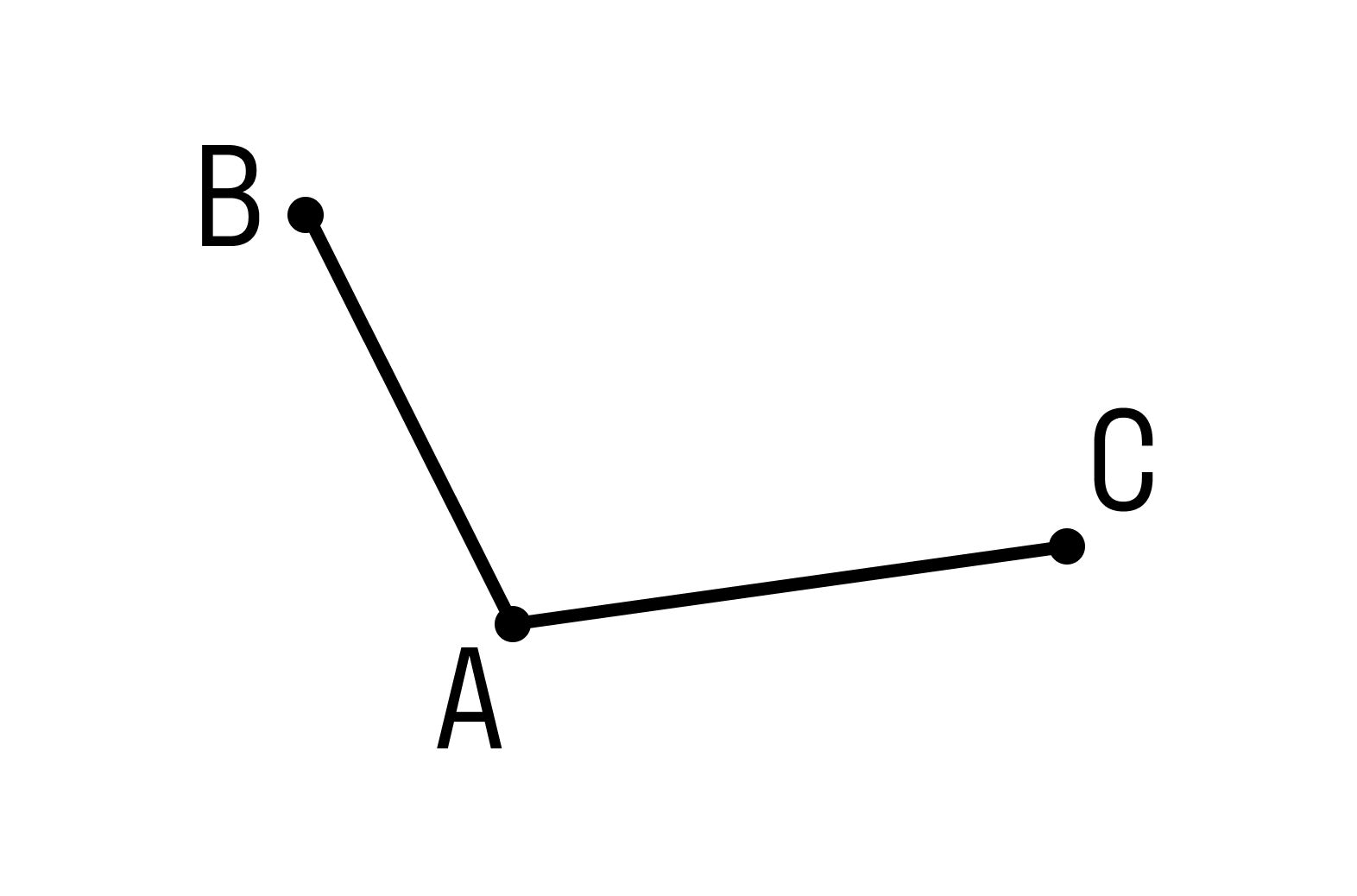
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.
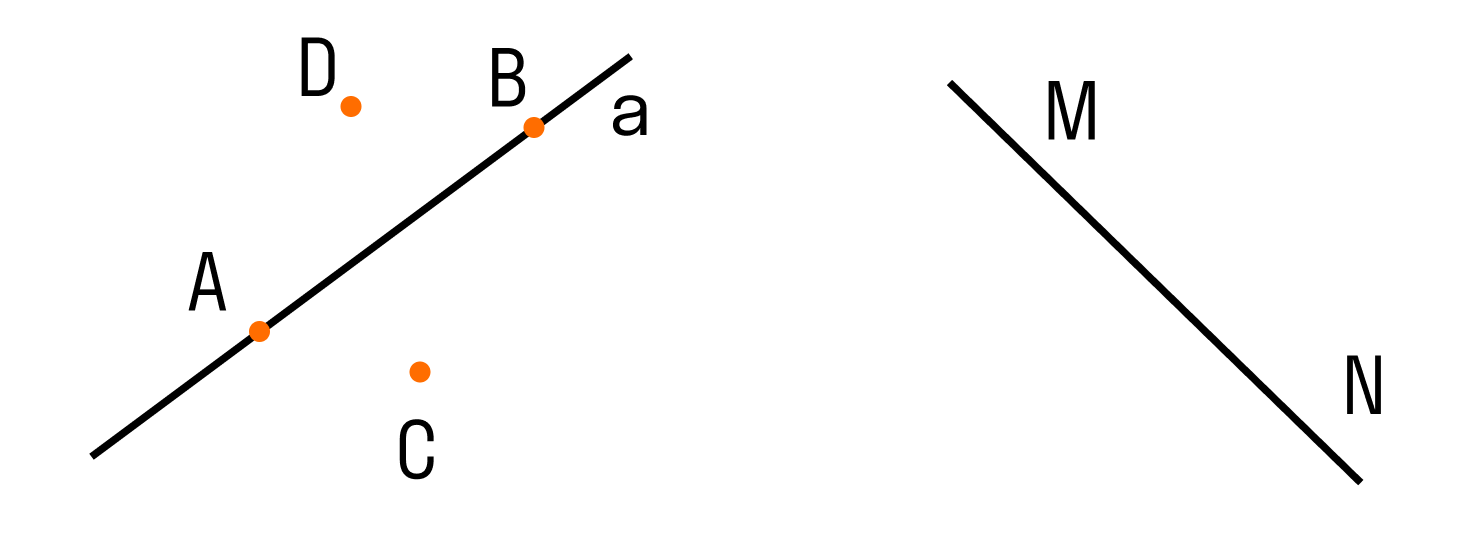
Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.
Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.
Обозначать прямые принято малыми латинскими буквами (a, b,c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).
Два варианта расположения точек относительно прямой:
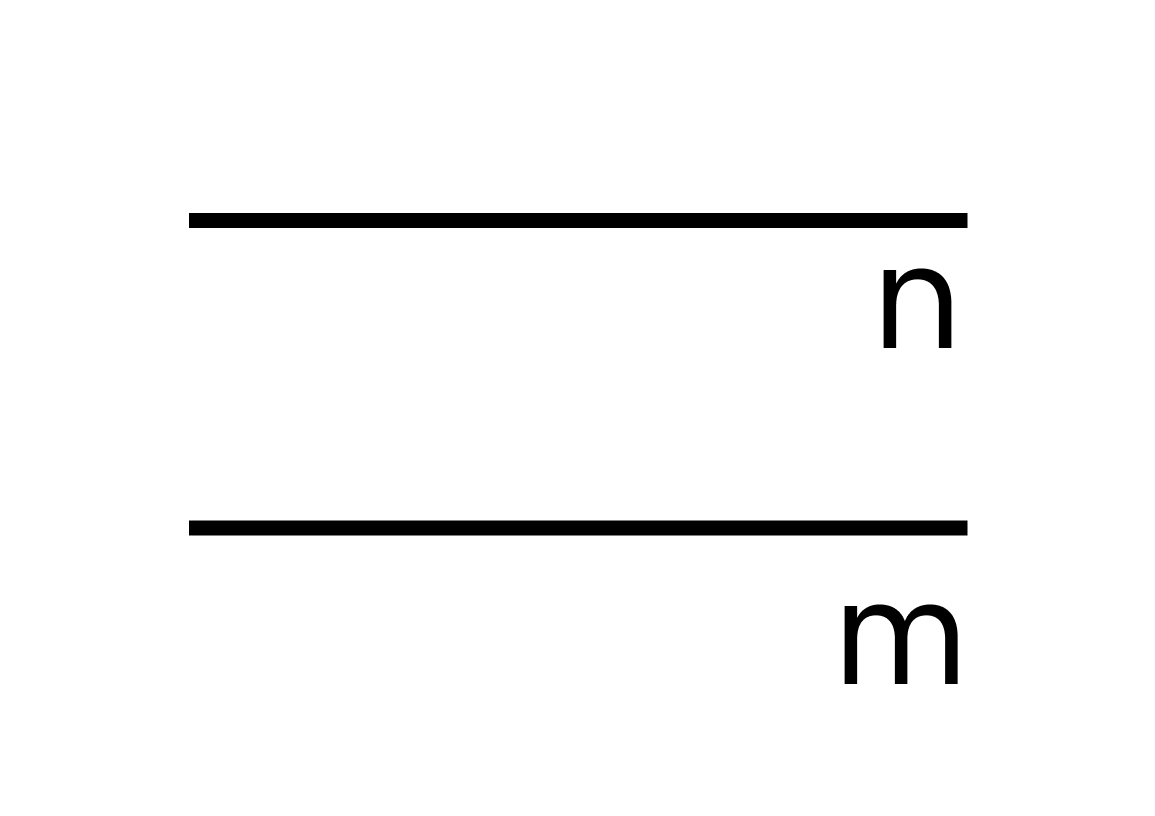
Если рассмотреть две прямые, то возможны два варианта их расположения:
Для записи не пересекающихся прямых используют специальный знак — 
то есть m 
Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.
На рисунке точка О разбивает прямую АВ на две части:
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.
Назовем получившиеся лучи:
Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.
Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости
Комбинации простейших объектов
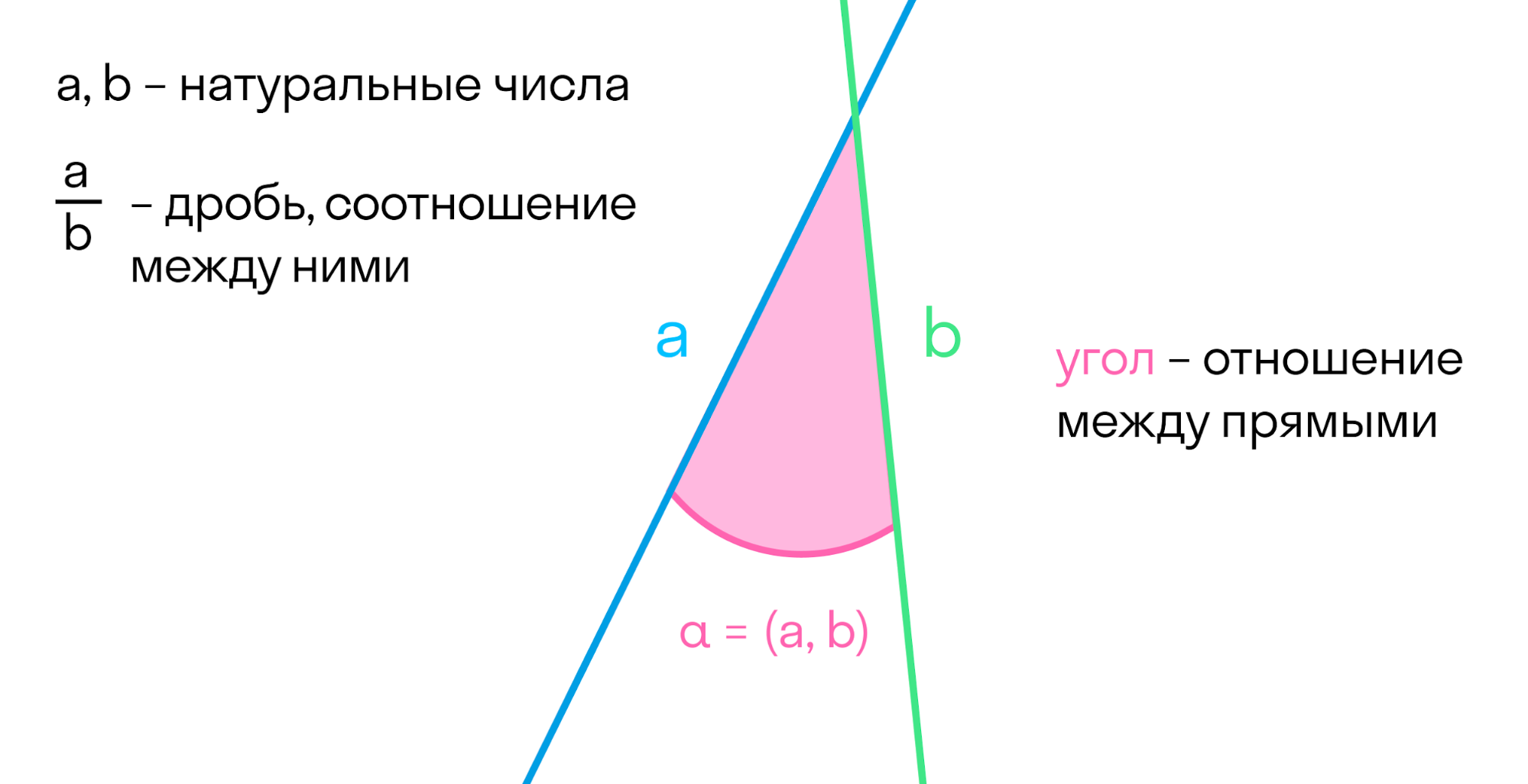
Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).
Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.
Точно так же мы изучали множества, а после — отношения между множествами, функции.
Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.
Максимальный угол – это полный оборот, он составляет 360 градусов.
Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.
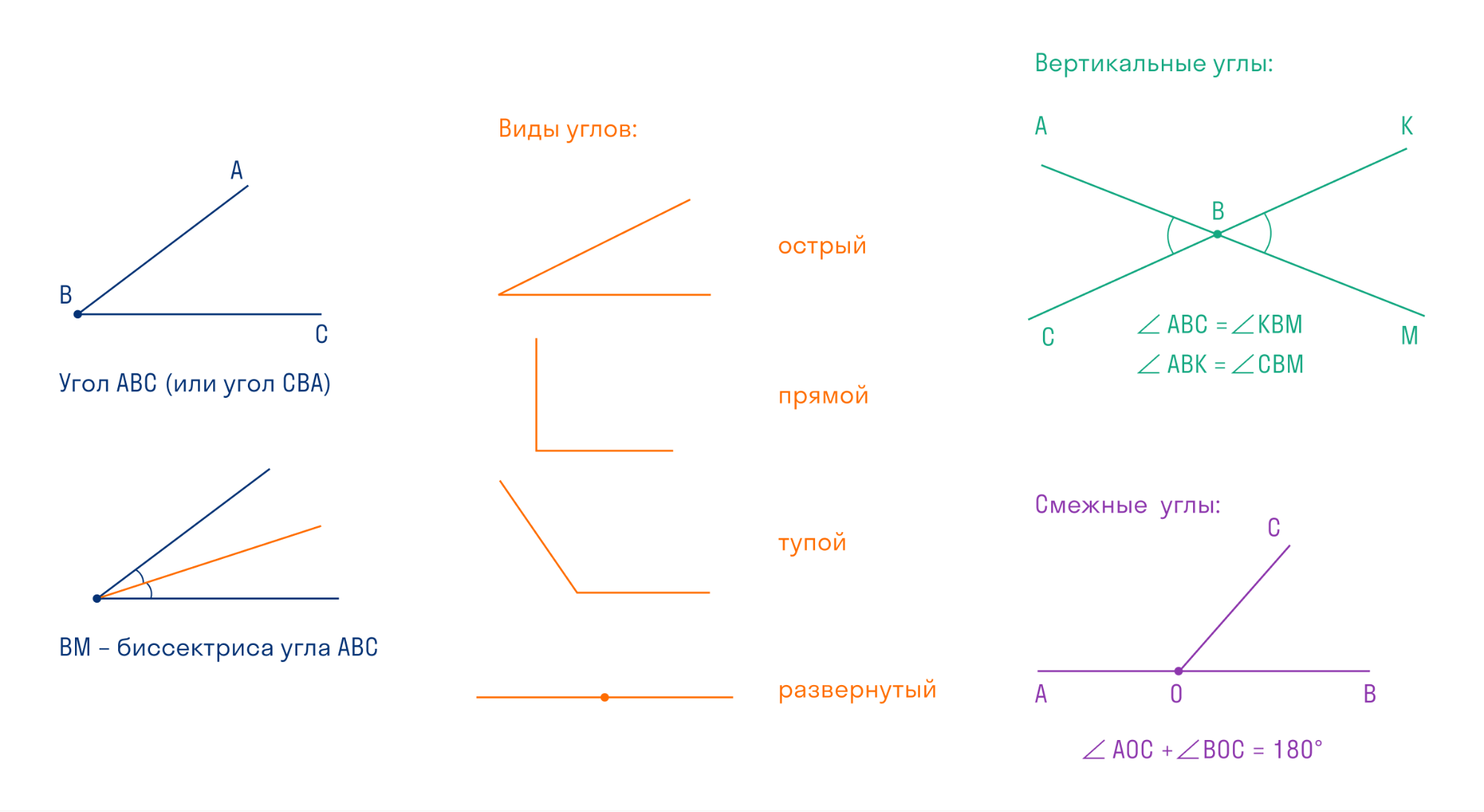
Есть разные виды углов, выделим самые часто встречающиеся:
Точка называется вершиной угла, а лучи — сторонами угла.
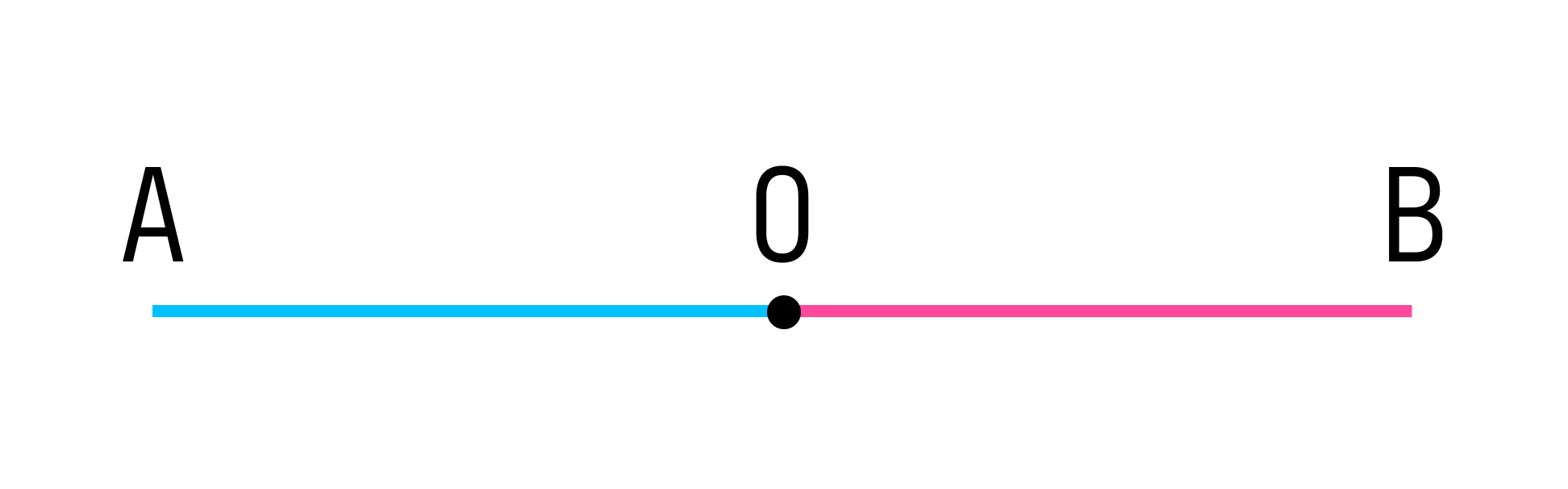
Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.
Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.
Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.
А теперь посмотрим на взаимное расположение трех прямых.
Первый случай: все три прямые параллельны.
Второй случай: две прямые параллельны, а третья их пересекает.
Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.
Треугольник
Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.
Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.
Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.
Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:
Приходи на наши онлайн уроки по математике с лучшими препадавателями! Для учеников с 1 по 11 классы!
Свойства треугольников
Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.
Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.
Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.
Сумма любых двух сторон треугольника больше его третьей стороны.
Еще одно свойство верное для всех треугольников: сумма всех углов треугольника составляет половину полного оборота. Или по-другому: сумма углов треугольника — два прямых угла.
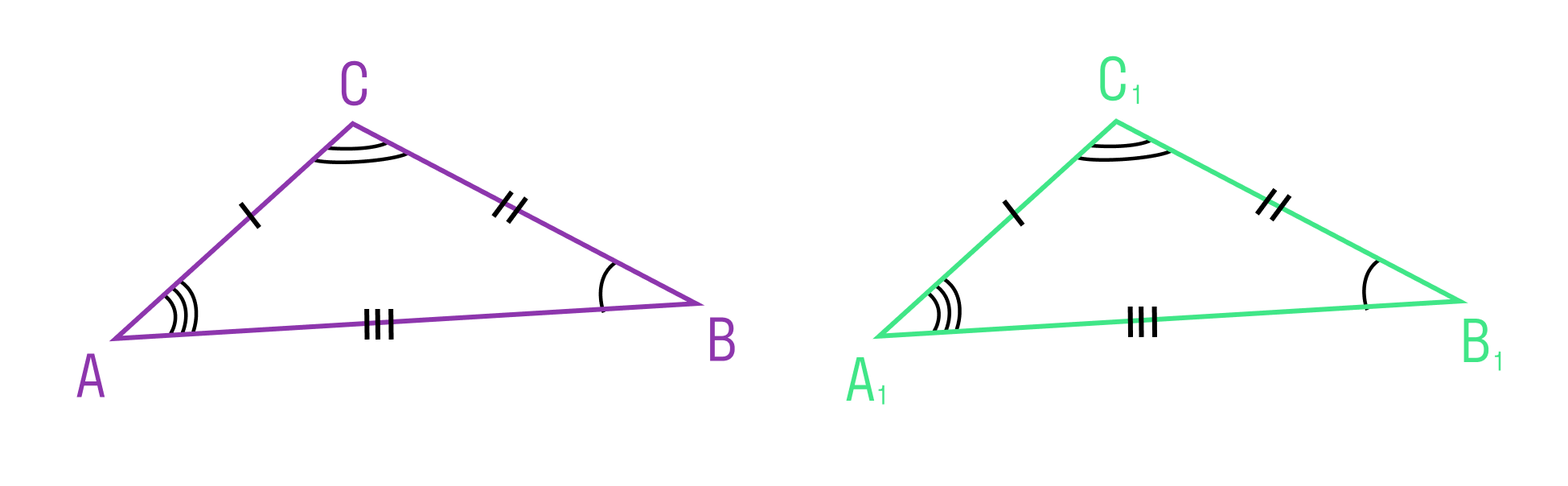
Мы знаем, что две геометрические фигуры считают равными, если их можно совместить наложением. Это справедливо и для треугольников. Равные фигуры имеют равные размеры и формы. Значит, если два треугольника равны — элементы одного треугольника соответственно равны элементам другого треугольника.
Равенство треугольников ABC и A1B1C1 обозначается так: ΔABC = ΔA1B1C1.
Есть даже специальные теоремы про равенство треугольников.
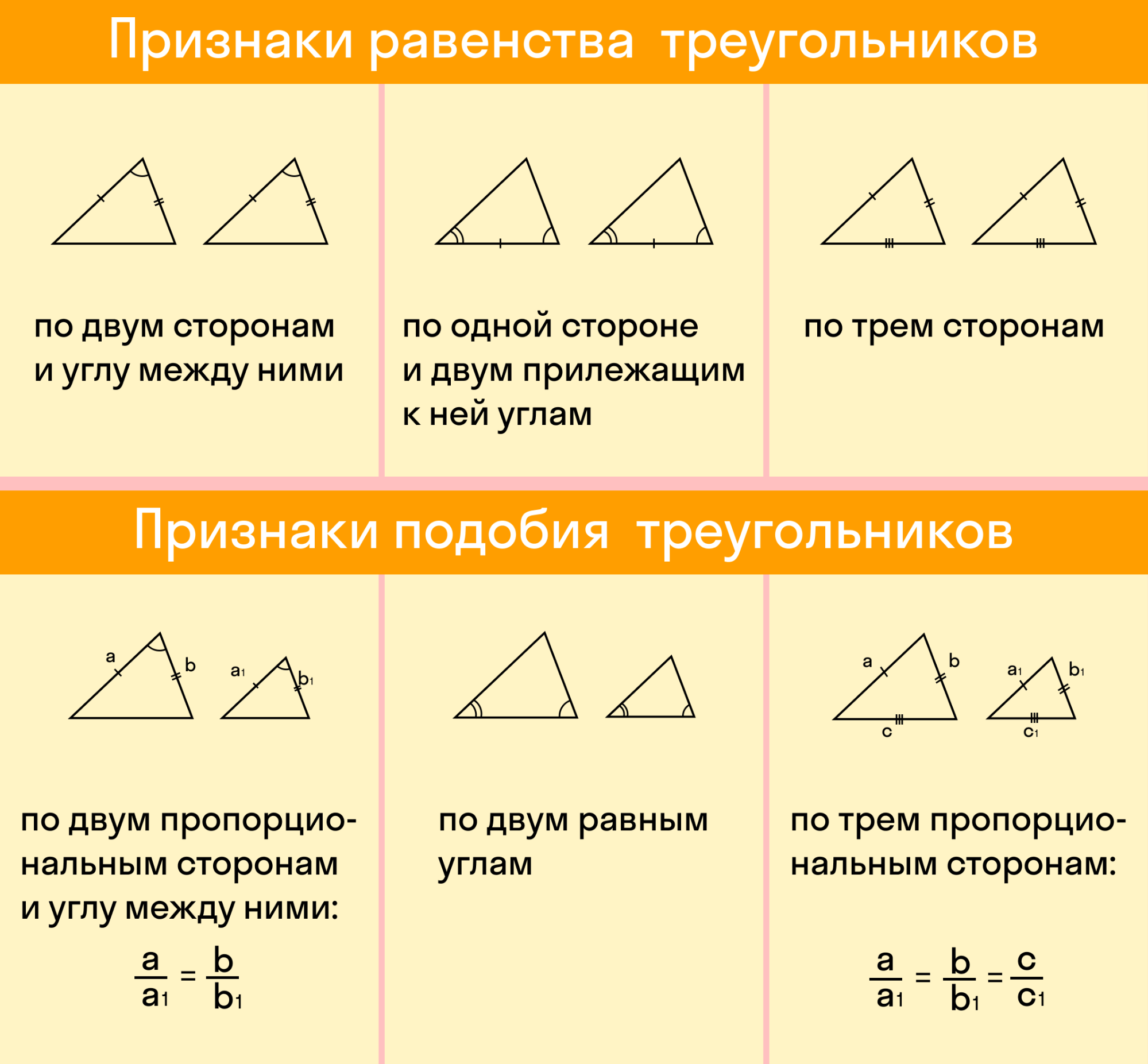
Первый признак равенства треугольников звучит так:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
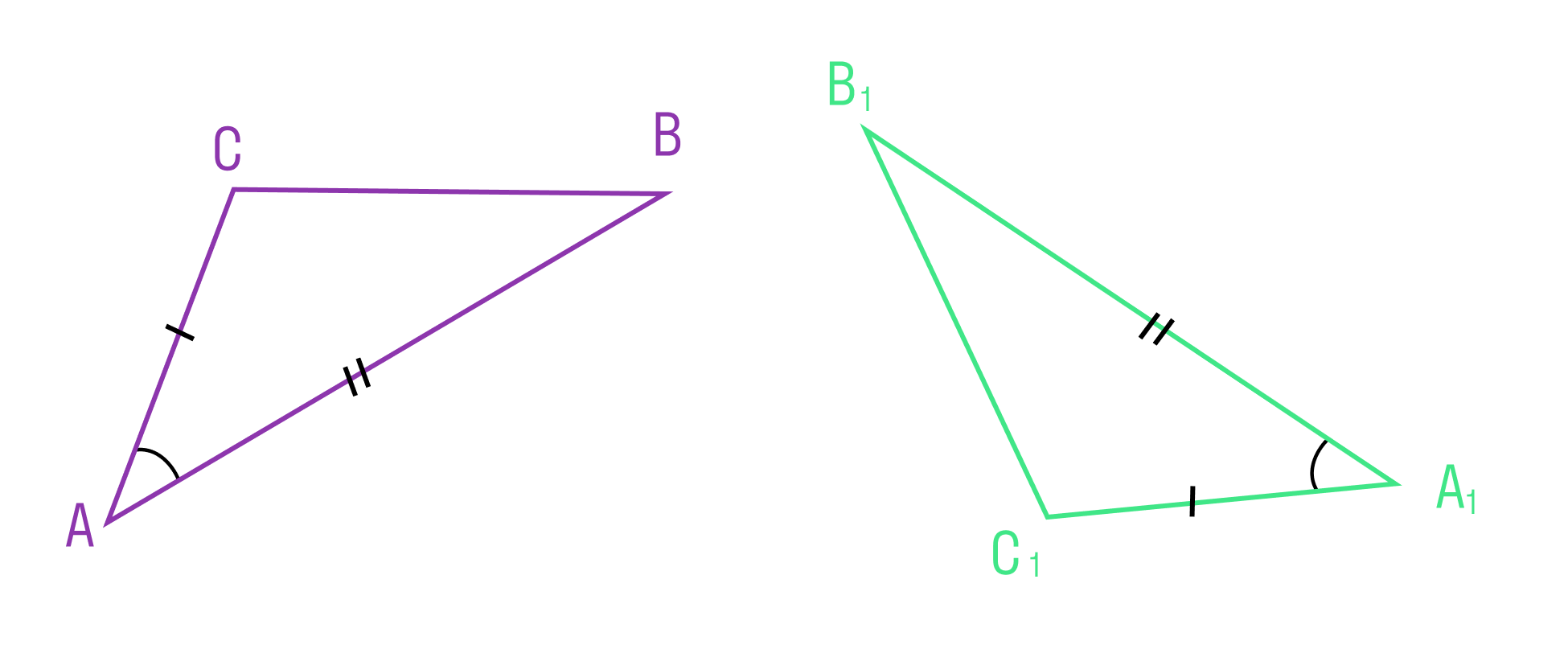
Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
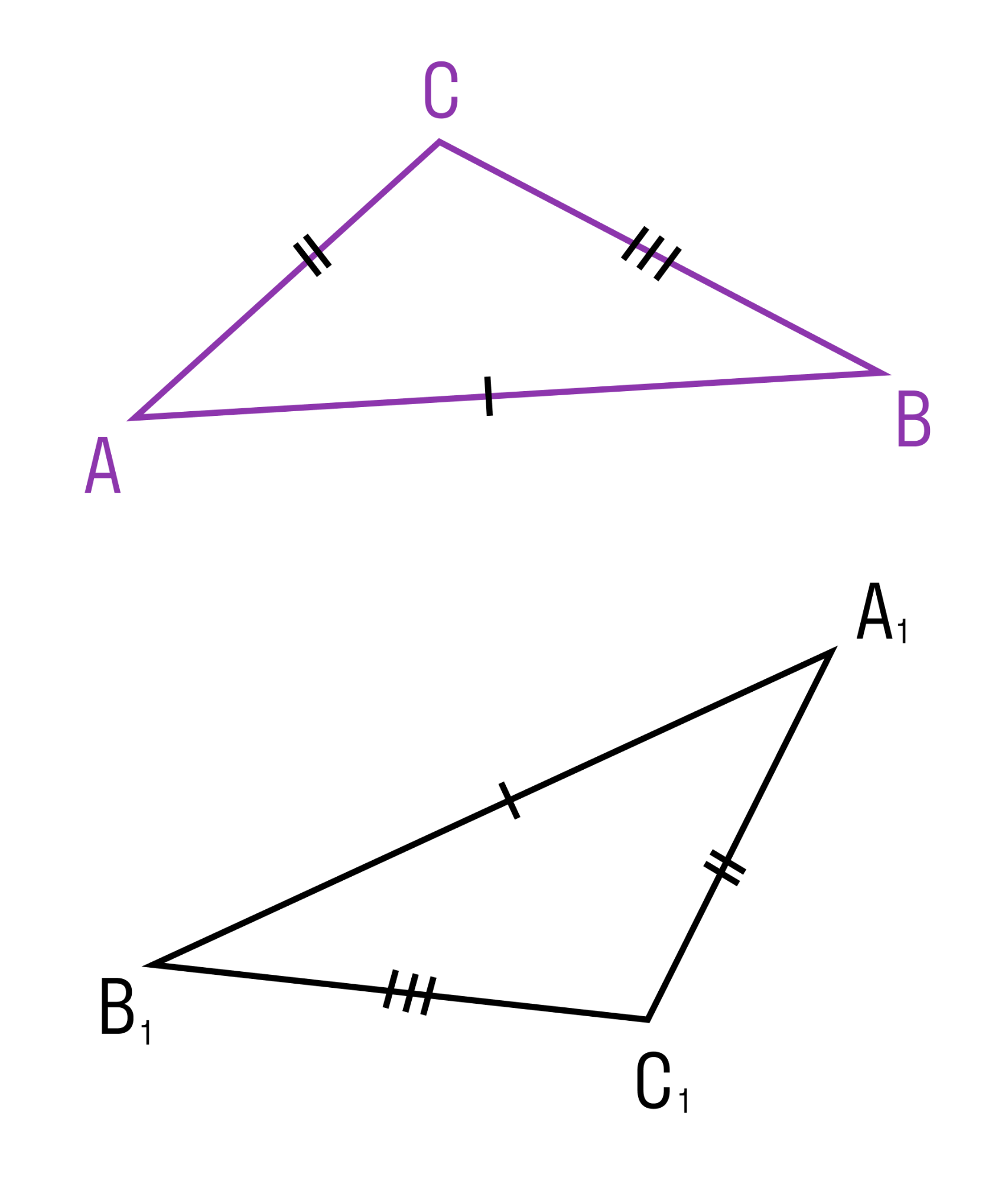
Третий признак равенства треугольников
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Из теоремы следует, что треугольник — жесткая фигура, то есть фигура, которую невозможно деформировать.
Подобные треугольники
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Треугольники АВС и A1B1C1 будут подобны, если
Число k, которое равно отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
Подобие треугольников обозначают специальным символом — ∾. На рисунке треугольники АВС и A1B1C1 подобны, это можно записать так: ΔАВС ∾ ΔA1B1C1.
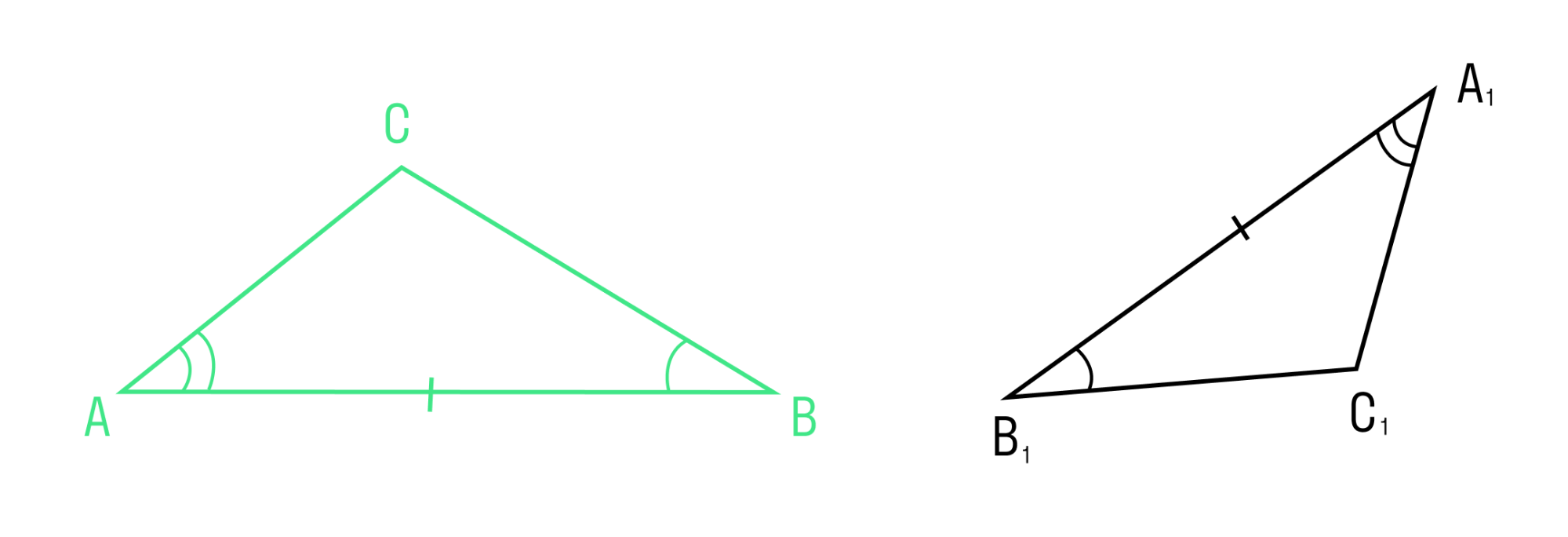
Теорема о первом признаке подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такое треугольники подобны.
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны — такие треугольники подобны.
Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
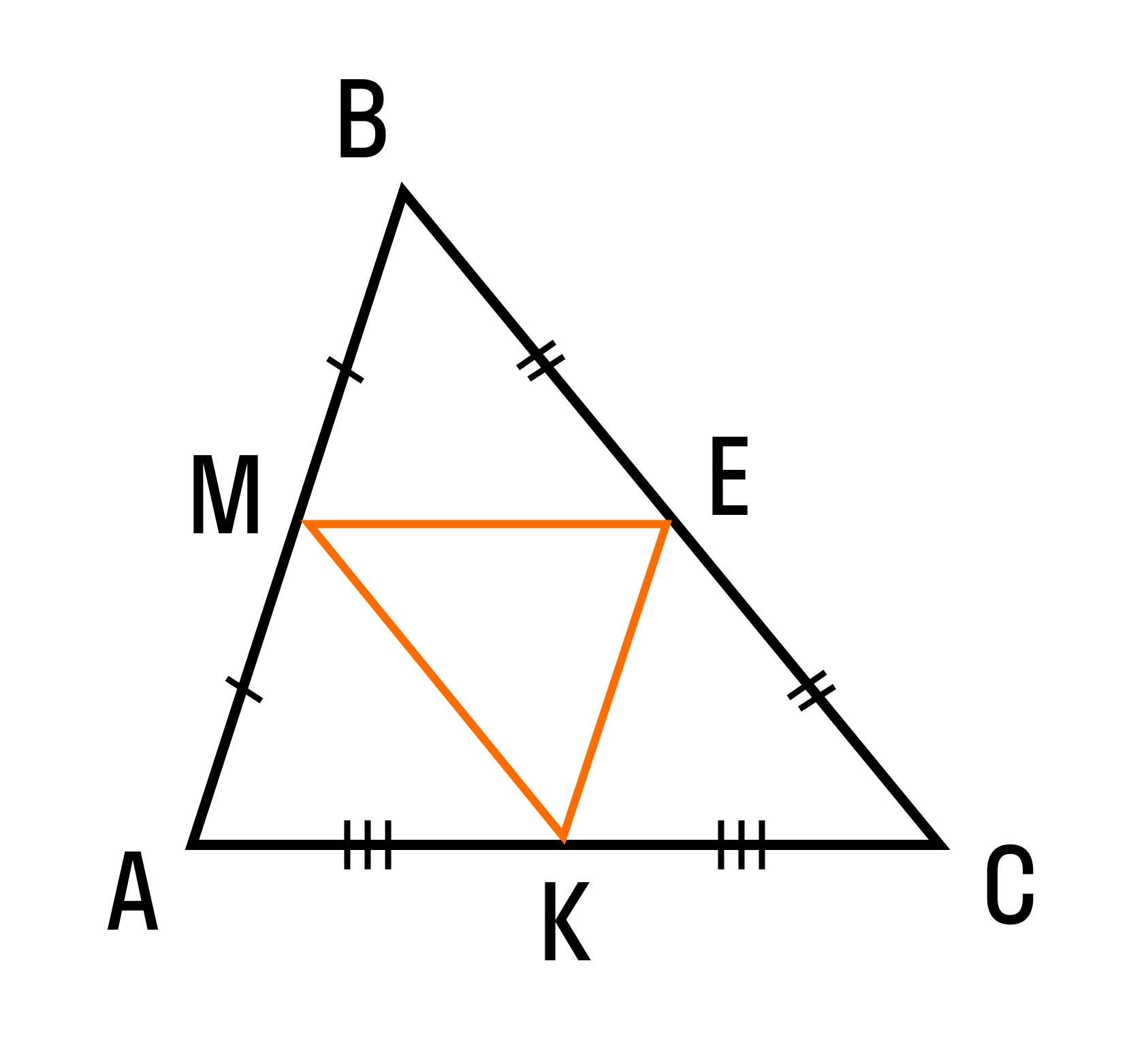
Средняя линия треугольника — это отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия 1/2.
На рисунке изображен треугольник АВС. Отрезки МЕ, МК и КЕ — средние линии данного треугольника, ΔВМЕ = ΔАМК = ΔСЕК = ΔМЕК.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
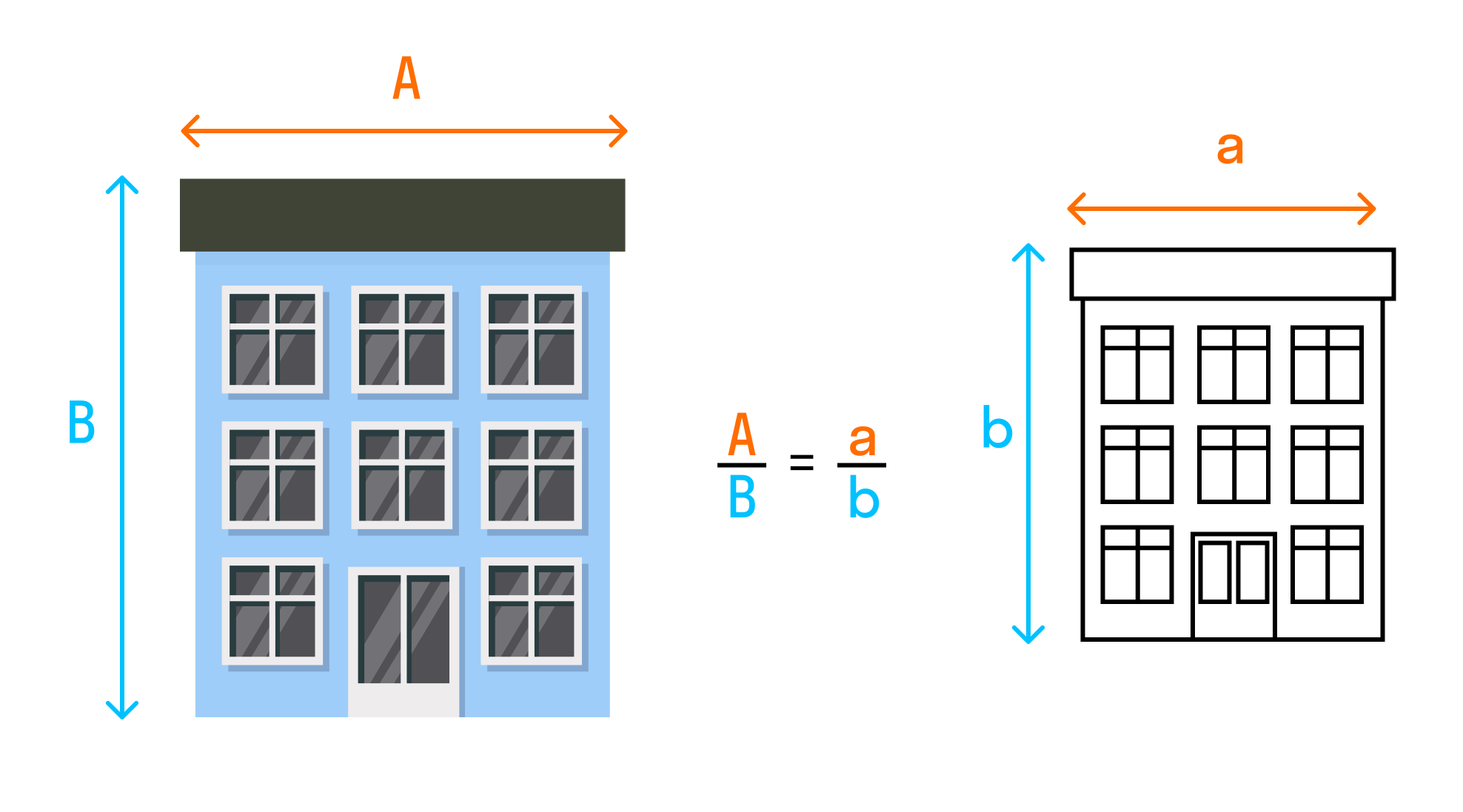
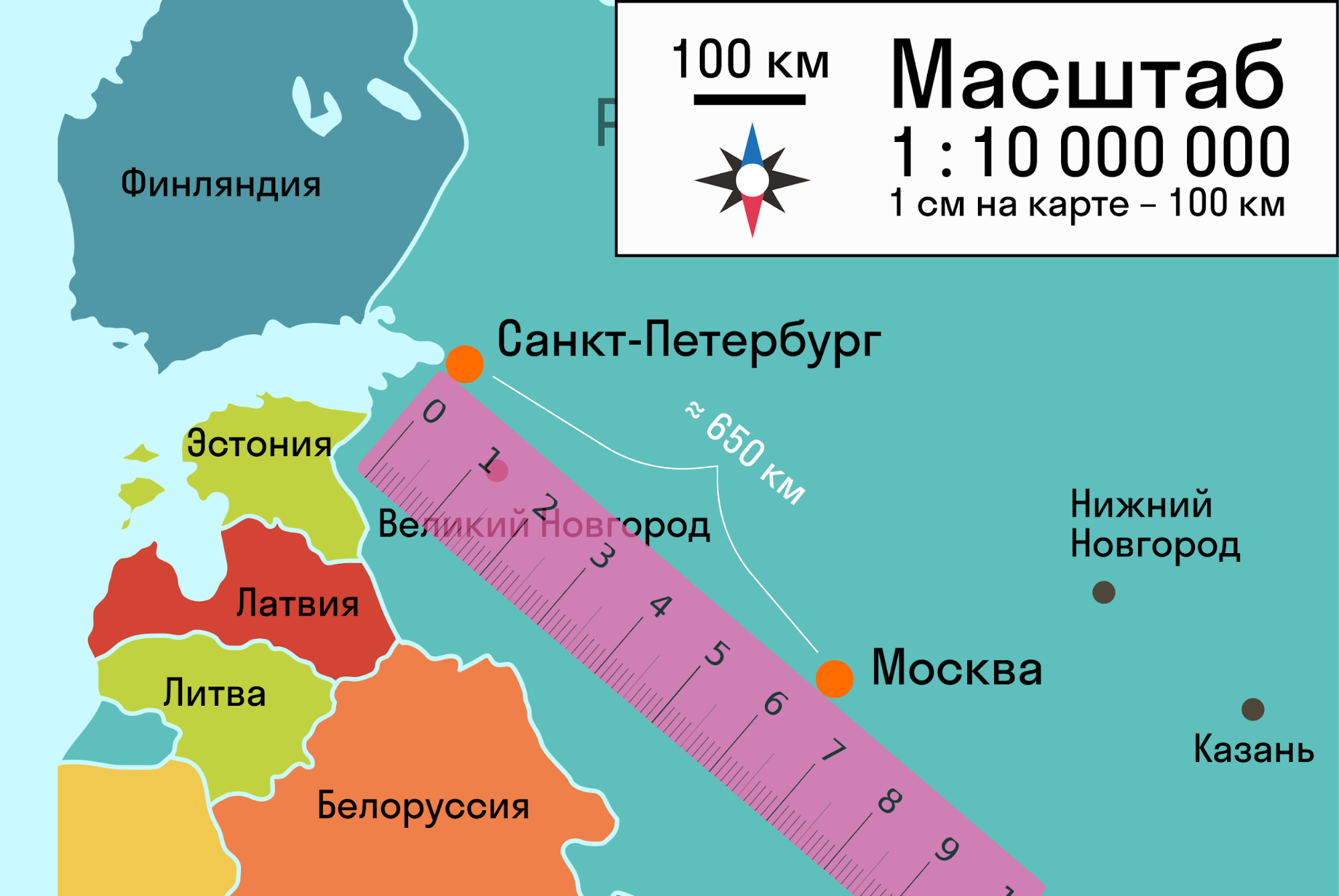
Важно понимать, что подобие в математике — это то, что в обычной жизни мы называем схожестью. Нарисовали треугольники или прямоугольники и говорим, что они похожи потому, что их стороны пропорциональны.
Пример подобия — карта. Она подобна местности, которую отражает. А масштаб — это и есть коэффициент подобия. С треугольниками или другими фигурами точно также.
Классификация треугольников по их сторонам
Для классификации треугольников можно использовать их типологию.
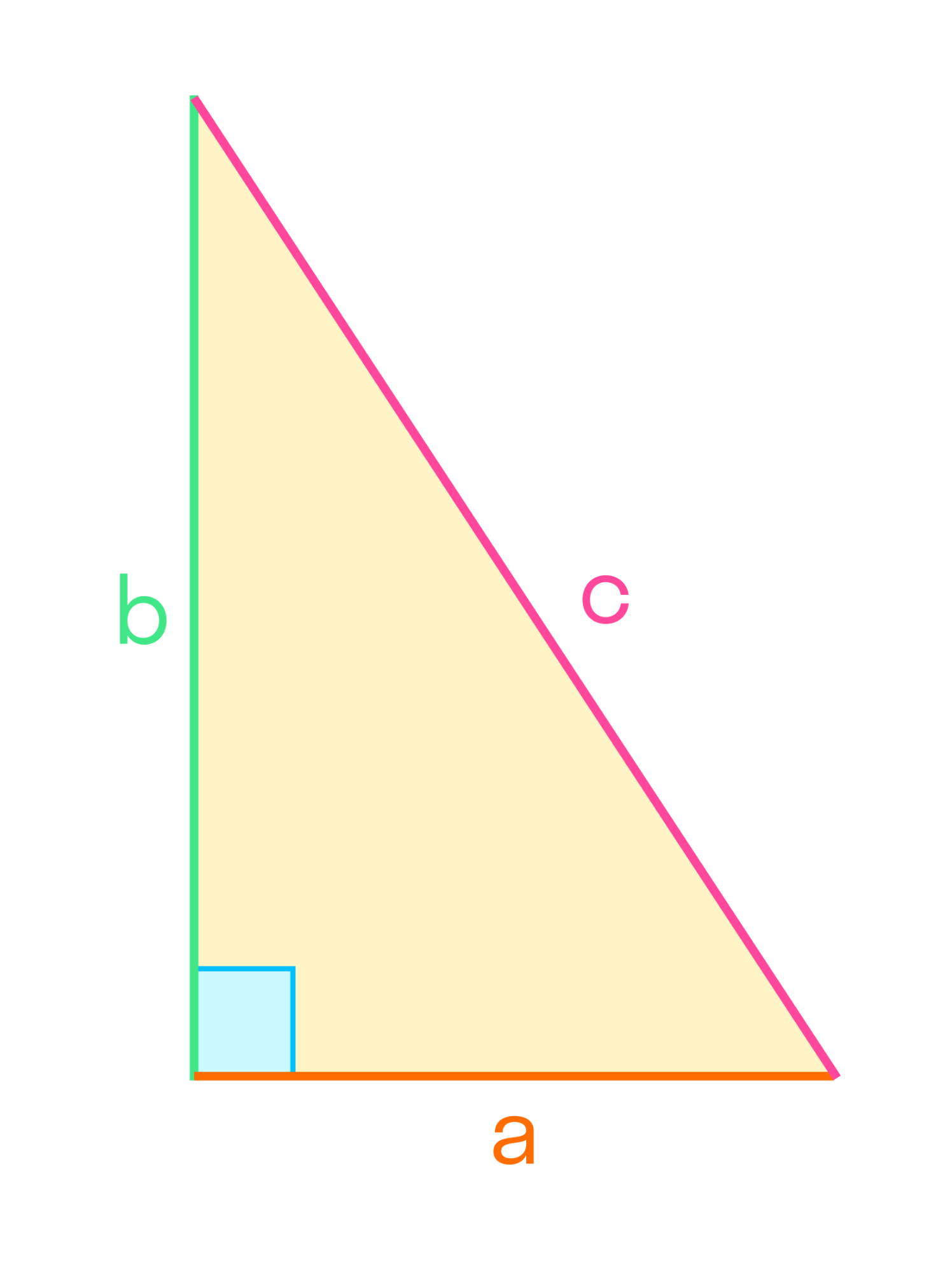
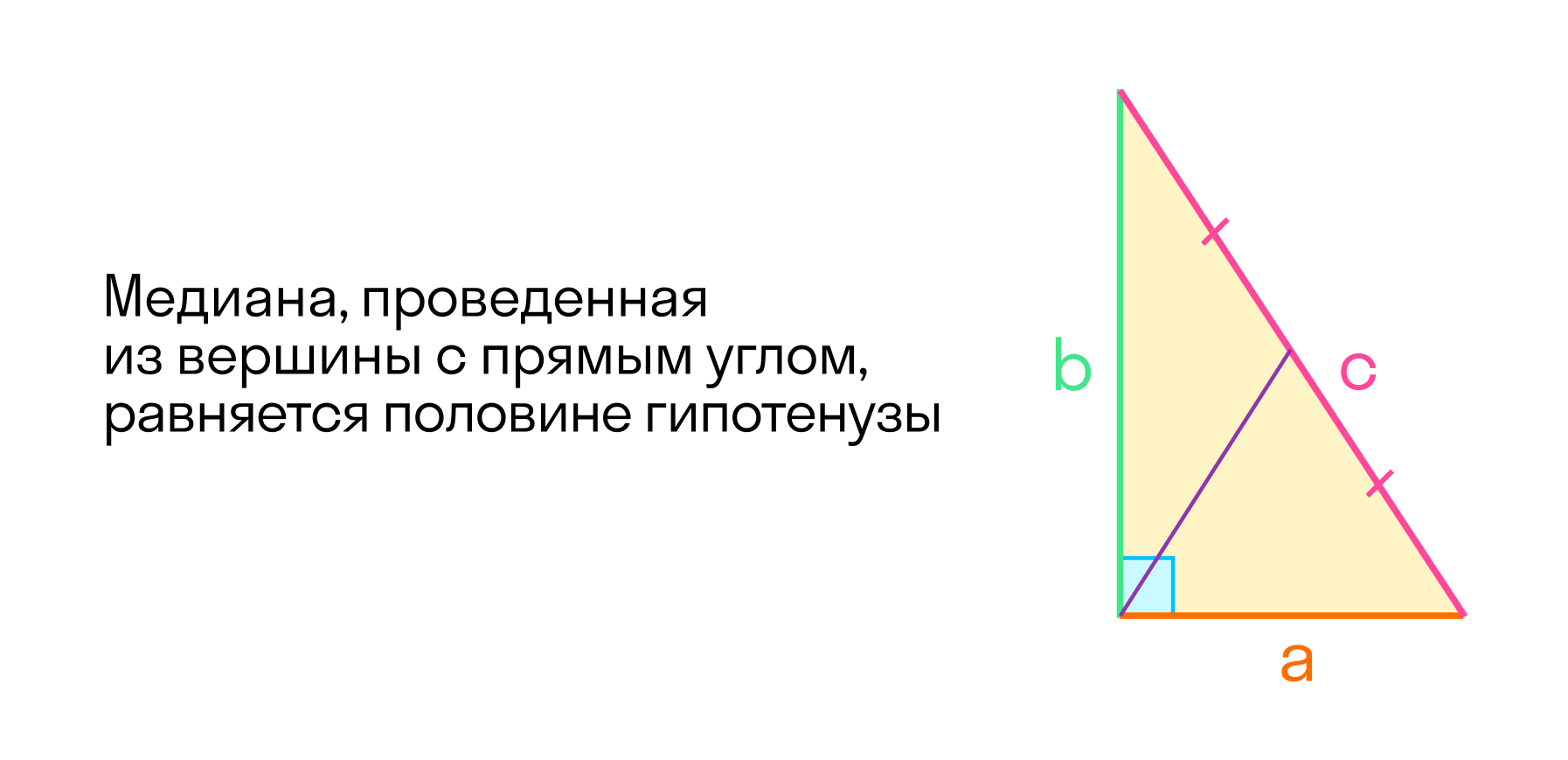
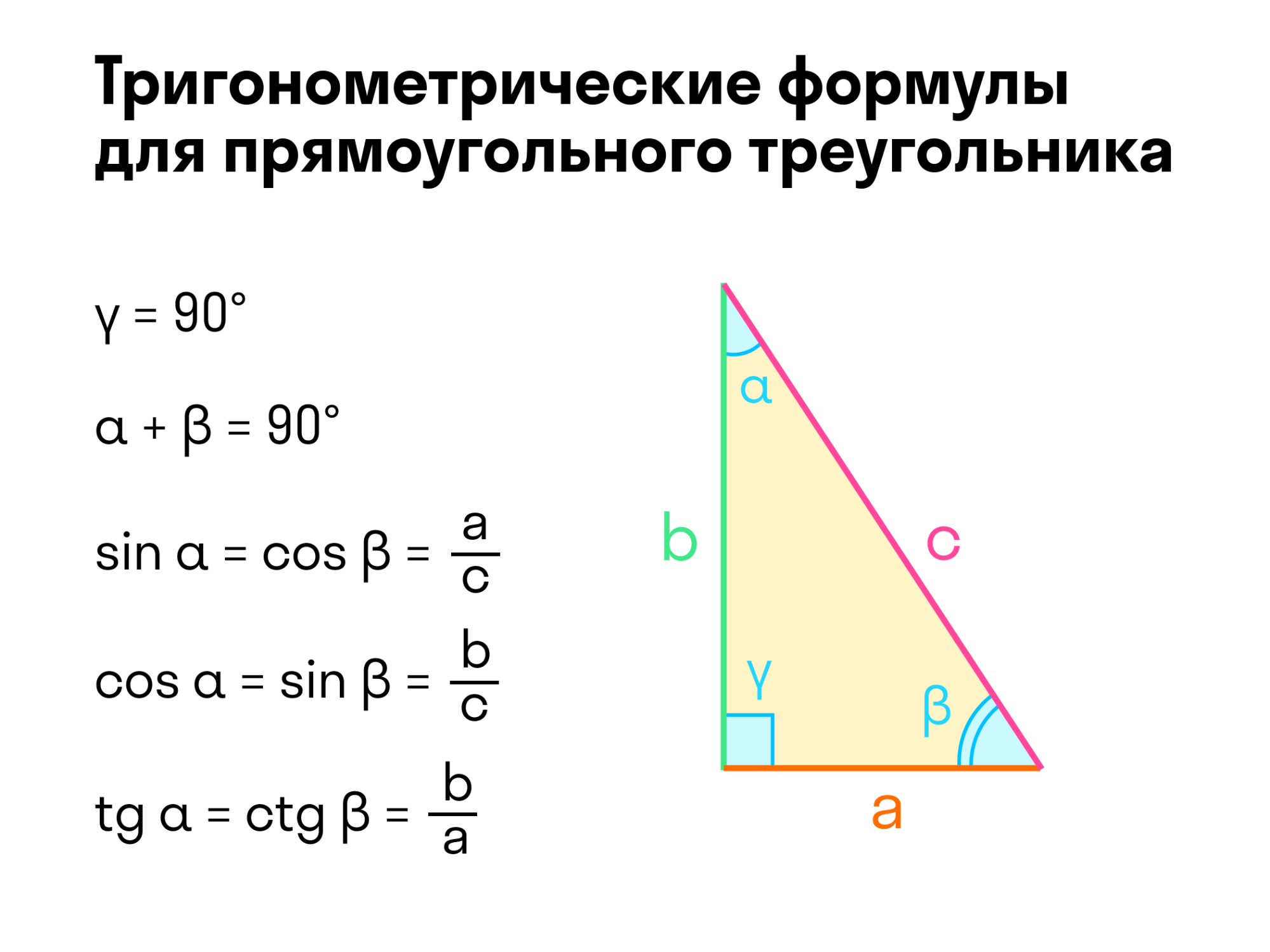
Один из распространенных типов — прямоугольный треугольник. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.
Свойства прямоугольного треугольника
С прямоугольных треугольников начинается изучение тригонометрии. Можно измерять углы с помощью отношений, использовать понятия синуса, косинуса. Помним, что угол можно задать двумя числами, их отношением.
Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.
Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.
Такой треугольник задается одним параметром — длиной стороны. Она полностью определяет все другие значения и размеры в этом треугольнике.
От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃
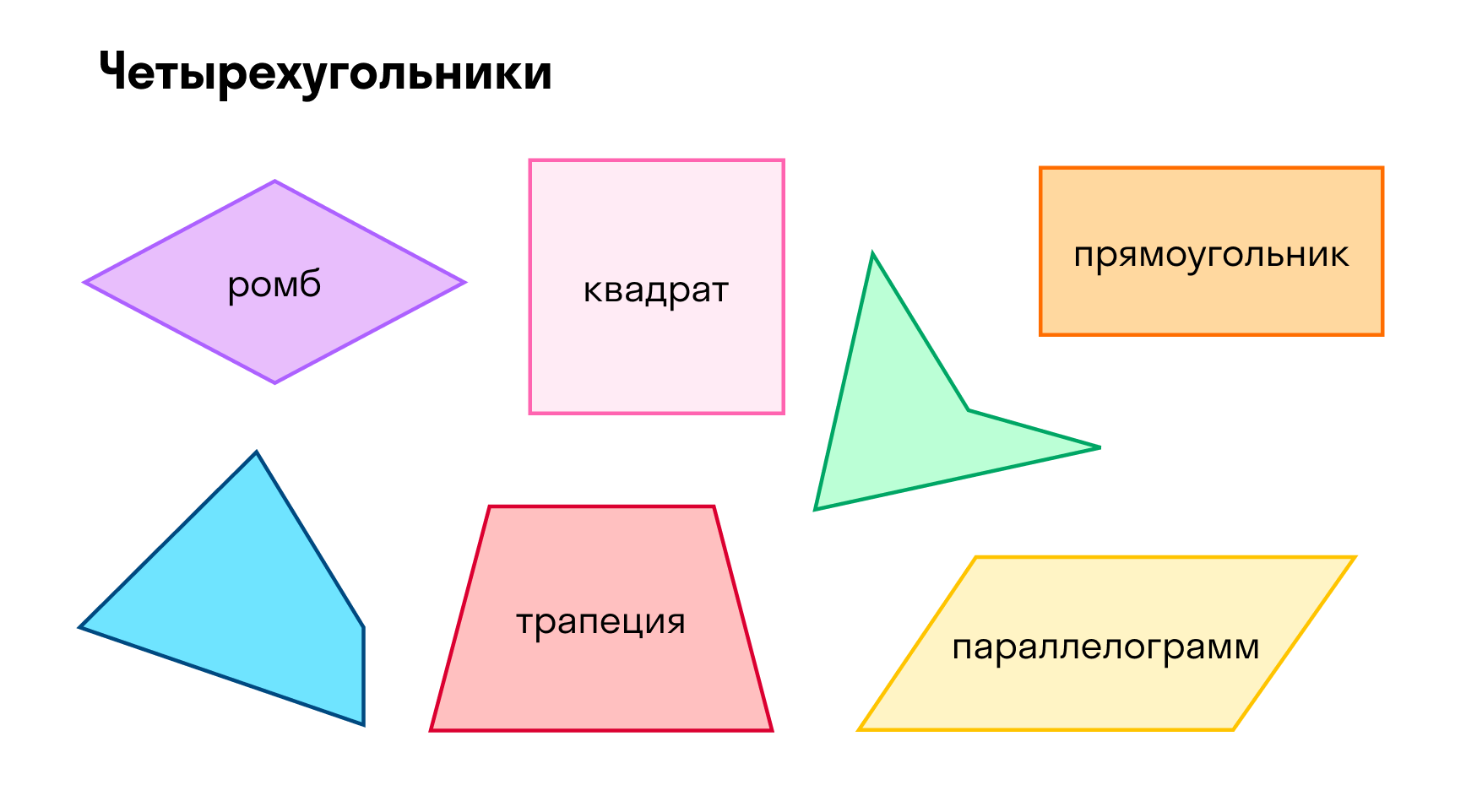
Четырехугольники
Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.
Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.
Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:
Окружность
Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.
Взаимодействие объектов
Следующий уровень — это взаимодействие всех-всех объектов, о которых мы говорили раньше.
Например, окружность и прямая. Прямая может находиться где-то в стороне от окружности, может ее пересекать, а может касаться, то есть пересекать в одной точке.
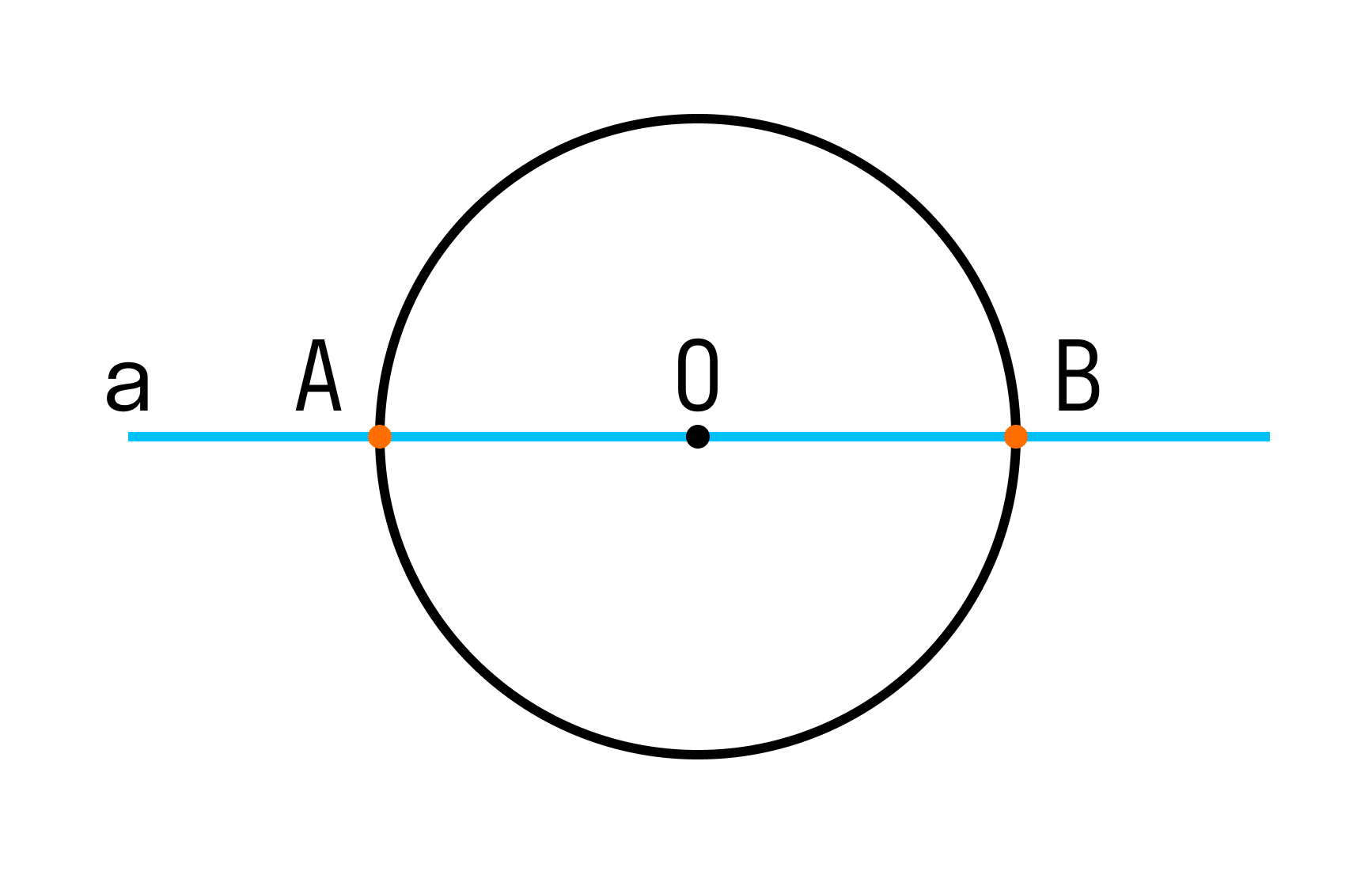
Если прямая проходит через центр окружности, то она пересекает окружность в двух точках — концах диаметра, который лежит на на этой прямой.
На рисунке прямая a проходит через центр окружности (точку О) и пересекает ее в двух точках А и В, которые являются концами диаметра АВ данной окружности.
Если прямая a не проходит через центр О окружности радиуса r, то возможны три случая взаимного расположения прямой и окружности — в зависимости от соотношения между радиусом r этой окружности и расстоянием d от центра окружности до прямой a. Вот эти случаи:
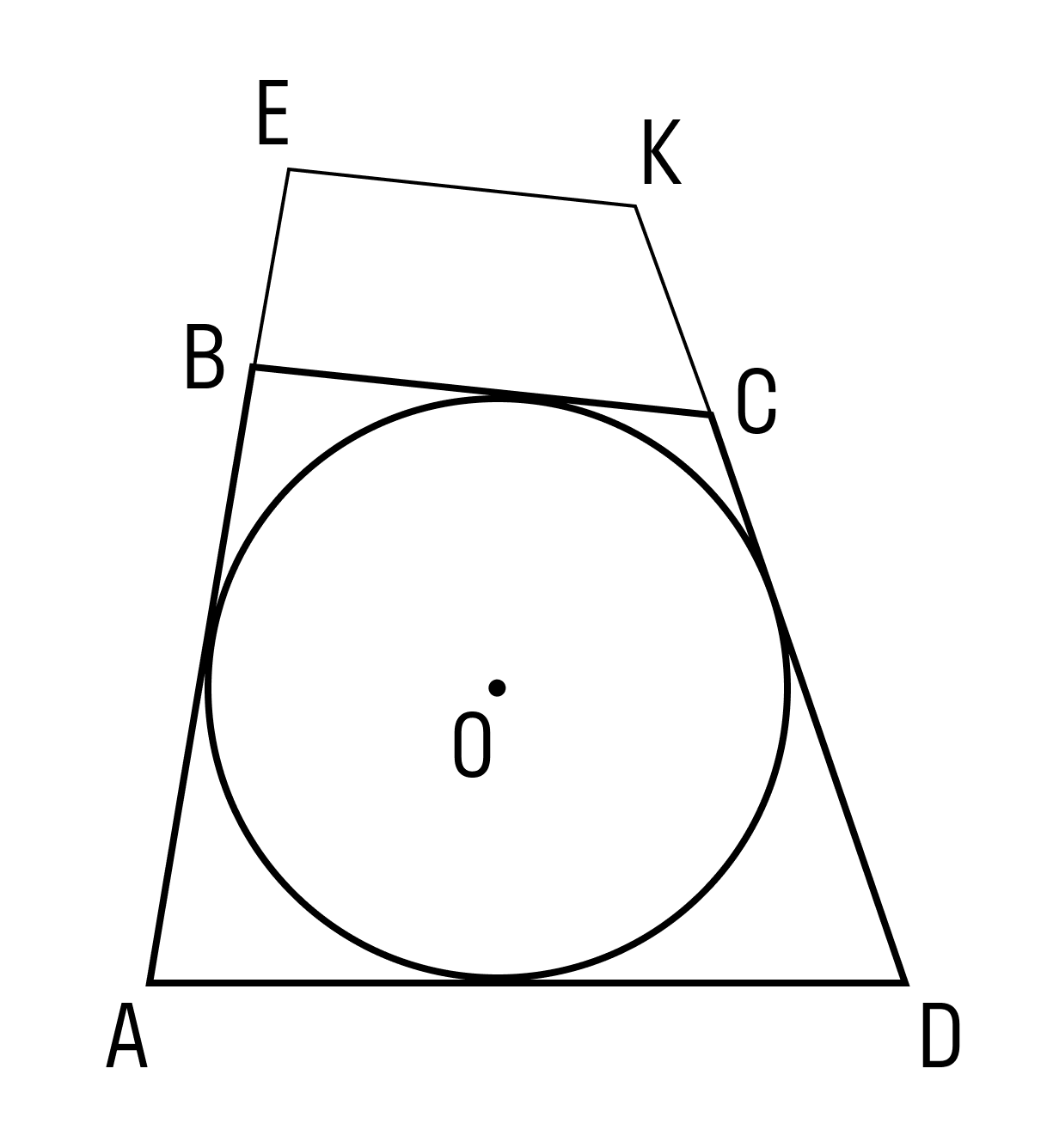
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность.
На рисунке четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.
В любой треугольник можно вписать только одну окружность, и вокруг любого ее можно описать.
Все это верно только для треугольников. Не в любой четырехугольник можно вписать окружность, и не вокруг любого можно описать. Более подробно эту тему можно изучить на уроках математики: признаки, теоремы и правила.
Практическая сторона геометрии
Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.
Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.
А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.
Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.
Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.
Почему изучать геометрию сложно: некоторые правила придется учить наизусть.
Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.