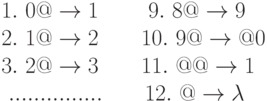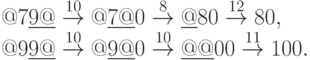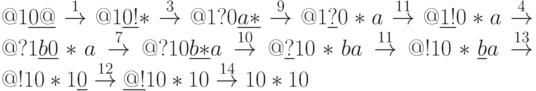Что такое нормальный алгоритм маркова
Нормальные алгоритмы Маркова
Определение нормального алгоритма и его выполнение
Шаг работы алгоритма повторяется до тех пор, пока
а при преобразовании слова abbc этот же алгоритм будет неограниченно работать, так как имеет место цикличное повторение данных:
Возможности нормальных алгоритмов и тезис Маркова
Пример 1. Рассмотрим простейшую операцию увеличения десятичного числа на 1. В этом случае почти всегда необходимо увеличить последнюю цифру на 1, а последняя цифра отличается тем, что после нее идет символ «@». Поэтому первыми подстановками должны быть подстановки типа
Но если это цифра 9, то ее нужно заменить 0 и увеличение на 1 перенести в предыдущий разряд. Этому отвечает подстановка
Наконец, если число начинается с 9 и перед этой цифрой нужно поставить 1, то этому будет отвечать подстановка
а если это не так, то в конце работы алгоритма символы @ надо стереть, что выполнит подстановка
Таким образом, мы получаем следующий НАМ увеличения десятичного числа на 1:
Приведем работу построенного алгоритма для чисел 79 и 99:
Аналогичным образом разрабатывается нормальный алгоритм Маркова для уменьшения числа на 1 (см. упражнение 1.3.1).
Продемонстрируем работу алгоритма для числа 10:
Вместе с тем построение алгоритма в последнем приведенном примере подсказывает следующую методику разработки НАМ :
Нормальный алгорифм Маркова
Норма́льный алгори́тм Ма́ркова — один из стандартизованных вариантов представления об алгорифме (алгоритме). Понятие нормального алгоритма введено А. А. Марковым в конце 1940-х годов.
Содержание
Описание
Нормальные алгоритмы являются вербальными, то есть предназначенными для применения к словам в различных алфавитах. Определение всякого нормального алгоритма состоит из двух частей: определения алфавита алгоритма (к словам в котором алгоритм будет применяться) и определения его схемы. Схемой нормального алгоритма называется конечный упорядоченный набор т. н. формул подстановки, каждая из которых может быть простой или заключительной. Простыми формулами подстановки называются слова вида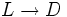 
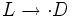
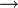
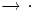
, где L и D — два произвольных слова в алфавите алгоритма (называемые, соответственно, левой и правой частями формулы подстановки). Аналогично, заключительными формулами подстановки называются слова вида 
, где L и D — два произвольных слова в алфавите алгоритма. При этом предполагается, что вспомогательные буквы 
и 
не принадлежат алфавиту алгоритма (в противном случае на исполняемую ими роль разделителя левой и правой частей следует избрать другие две буквы).
Примером схемы нормального алгоритма в пятибуквенном алфавите | * abc может служить схема
Любой нормальный алгорифм эквивалентен некоторой машине Тьюринга, и наоборот — любая машина Тьюринга эквивалентна некоторому нормальному алгорифму. Вариант тезиса Чёрча — Тьюринга, сформулированный применительно к нормальным алгорифмам, принято называть «принципом нормализации».
Нормальные алгорифмы оказались удобным средством для построения многих разделов конструктивной математики. Кроме того, заложенные в определении нормального алгорифма идеи используются в ряде ориентированных на обработку символьной информации языков программирования — например, в языке Рефал.
Примеры
Пример 1
Использование алгоритма Маркова для преобразований над строками:
«Я купил кг Аов в Т М.»
При выполнении алгоритма строка претерпевает следующие изменения:
На этом выполнение алгоритма завершится (так как будет достигнута формула №5, которую мы сделали заключительной).
Пример 2
Этот набор правил делает более интересную вещь. Он преобразует двоичные числа в «единичные», то есть на выходе получается строка из N единичек, если на входе у нас было N в двоичной системе. Например, 101 преобразуется в 5 единиц:
Нормальный алгоритм Маркова
Норма́льный алгори́тм Ма́ркова — один из стандартизованных вариантов представления об алгорифме (алгоритме). Понятие нормального алгоритма введено А. А. Марковым в конце 1940-х годов.
Содержание
Описание
Нормальные алгоритмы являются вербальными, то есть предназначенными для применения к словам в различных алфавитах. Определение всякого нормального алгоритма состоит из двух частей: определения алфавита алгоритма (к словам в котором алгоритм будет применяться) и определения его схемы. Схемой нормального алгоритма называется конечный упорядоченный набор т. н. формул подстановки, каждая из которых может быть простой или заключительной. 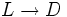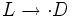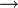Простыми формулами подстановки называются слова вида , где L и D — два произвольных слова в алфавите алгоритма (называемые, соответственно, левой и правой частями формулы подстановки). Аналогично, заключительными формулами подстановки называются слова вида , где L и D — два произвольных слова в алфавите алгоритма. При этом предполагается, что вспомогательные буквы и не принадлежат алфавиту алгоритма (в противном случае на исполняемую ими роль разделителя левой и правой частей следует избрать другие две буквы).
Примером схемы нормального алгоритма в пятибуквенном алфавите | * abc может служить схема
Любой нормальный алгорифм эквивалентен некоторой машине Тьюринга, и наоборот — любая машина Тьюринга эквивалентна некоторому нормальному алгорифму. Вариант тезиса Чёрча — Тьюринга, сформулированный применительно к нормальным алгорифмам, принято называть «принципом нормализации».
Нормальные алгорифмы оказались удобным средством для построения многих разделов конструктивной математики. Кроме того, заложенные в определении нормального алгорифма идеи используются в ряде ориентированных на обработку символьной информации языков программирования — например, в языке Рефал.
Примеры
Пример 1
Использование алгоритма Маркова для преобразований над строками:
«Я купил кг Аов в Т М.»
При выполнении алгоритма строка претерпевает следующие изменения:
На этом выполнение алгоритма завершится (так как будет достигнута формула №5, которую мы сделали заключительной).
Пример 2
Этот набор правил делает более интересную вещь. Он преобразует двоичные числа в «единичные», то есть на выходе получается строка из N единичек, если на входе у нас было N в двоичной системе. Например, 101 преобразуется в 5 единиц:
Нормальные алгоритмы Маркова
Определение нормального алгоритма и его выполнение
Шаг работы алгоритма повторяется до тех пор, пока
а при преобразовании слова abbc этот же алгоритм будет неограниченно работать, так как имеет место цикличное повторение данных:
Возможности нормальных алгоритмов и тезис Маркова
Пример 1. Рассмотрим простейшую операцию увеличения десятичного числа на 1. В этом случае почти всегда необходимо увеличить последнюю цифру на 1, а последняя цифра отличается тем, что после нее идет символ «@». Поэтому первыми подстановками должны быть подстановки типа
Но если это цифра 9, то ее нужно заменить 0 и увеличение на 1 перенести в предыдущий разряд. Этому отвечает подстановка
Наконец, если число начинается с 9 и перед этой цифрой нужно поставить 1, то этому будет отвечать подстановка
а если это не так, то в конце работы алгоритма символы @ надо стереть, что выполнит подстановка
Таким образом, мы получаем следующий НАМ увеличения десятичного числа на 1:
Приведем работу построенного алгоритма для чисел 79 и 99:
Аналогичным образом разрабатывается нормальный алгоритм Маркова для уменьшения числа на 1 (см. упражнение 1.3.1).
Продемонстрируем работу алгоритма для числа 10:
Вместе с тем построение алгоритма в последнем приведенном примере подсказывает следующую методику разработки НАМ :
Нормальные алгоритмы Маркова
Вы будете перенаправлены на Автор24
Нормальные алгоритмы Маркова — это стандартный метод формализованного определения понятия алгоритма.
Теоретические основы нормальных алгоритмов были сформулированы видным математиком Советского Союза А.А. Марковым в конце сороковых годов двадцатого века. Они явились некоторыми базовыми правилами по обработке словесных символов в каких-либо алфавитах, то есть начальными информационными данными и итоговыми результатами таких алгоритмов выступали буквы некоторого алфавита.
Подстановки Маркова
Подстановкой Маркова является процедура над словами, которая выполняется при помощи двух упорядоченных слов (P, Q), и состоит в таких действиях. В выбранном слове R определяется первое вхождение слова P (при наличии такого) и, без коррекции других фрагментов слова R, подменяют в нём данное вхождение словом Q. Сформированное в итоге слово является результатом использования подстановки Маркова (P, Q) к слову R. В случае отсутствия первого вхождения P в слово R, то есть вхождения полностью отсутствуют, то это означает неприменимость подстановки Маркова (P, Q) к слову R.
Частным случаем подстановок Маркова считаются подстановки с использованием пустых слов:
Ниже в таблице приведены примеры подстановок Маркова, во всех строках которой вначале приведено слово, подлежащее преобразованию, далее применимая к этому слову подстановка Маркова и в конце сформированное в итоге слово:
Рисунок 1. Примеры подстановок Маркова. Автор24 — интернет-биржа студенческих работ
Готовые работы на аналогичную тему
Чтобы обозначить Марковскую подстановку (P, Q), применяется запись P → Q. Она носит название формулы подстановки (P, Q). Отдельные подстановки (P, Q) называются заключительными. Чтобы обозначить такие подстановки применяется запись P → Q, которая называется формулой заключительной подстановки. Слово P является левой частью, а слово Q считается правой частью в формуле подстановки.
Нормальные алгоритмы Маркова
Финальный перечень формул подстановок после упорядочения представлен ниже:
Данный упорядоченный конечный перечень формул подстановок в алфавите A именуется записью нормального алгоритма в A. Точка, взятая в скобки, показывает, что её в этом месте может и не быть. Приведённая схема даёт определение алгоритма преобразования слов, который называется нормальным алгоритмом Маркова. Сформулируем более точное понимание нормального алгоритма Маркова.
Нормальным алгоритмом Маркова в алфавите А является определённый закон формирования очерёдности слов Vi в алфавите A, на основании заданного слова V в выбранном алфавите. Начальным словом V0 очерёдности слов назначается слово V. Предположим, что некоторого значения i ≥ 0 слово Vi сформировано, и процедура реализации данной последовательности пока не завершена. В случае отсутствия в схеме нормального алгоритма формул, у которых левая часть вошла бы в Vi, то Vi+1 считается равным Vi, что даёт право считать процедуру формирования последовательности завершённой. Но когда в схеме присутствуют формулы, у которых левые части входят в Vi, то за значение Vi+1 принимается итог подстановки Маркова правой части начальной в этих формулах, замещая первое вхождение её левой части в слово. Процедура формирования последовательности может считаться завершённой, когда в текущем шаге использовалась формула финальной подстановки, в противном случае процесс продолжает выполняться. В случае обрыва процедуры формирования упомянутой последовательности, то считается, что текущий нормальный алгоритм можно применить к слову V. Оконечный элемент W последовательности является итогом использования нормального алгоритма к слову V. То есть, по сути, при помощи нормального алгоритма перерабатывается V в W.
Последовательность Vi записывается в таком порядке:
V0 ⇨ V1 ⇨ V2 ⇨ … ⇨ Vm-1 ⇨ Vm.
Здесь V0 = V, а Vm = W.
Это определение является понятием нормального алгоритма в алфавите A. В случае задания алгоритма в каком-либо алфавитном расширении A, то считается, что он является нормальным алгоритмом над A.
Приведём пример нормального алгоритма. Имеется алфавит A =
Задаваемый данной схемой алгоритм работает следующим образом. Любое слово V в алфавите A, которое содержит даже единственное вхождение буквы a, алгоритм переработает в слово, формирующееся из V путём вычёркивания в нём самого первого вхождения символа a. А если слово является пустым, то алгоритм выполняет его переработку также в пустое. Данный алгоритм не может быть использован со словами, содержащими лишь только букву b. К примеру:
aabab ⇨ abab, ab ⇨ b, aa ⇨ a, bbab ⇨ bbb, baba ⇨ bba.
Аналогично машине Тьюринга, нормальные алгоритмы, по сути, не выполняют отдельных вычислительных операций. Они только осуществляют операции по преобразованию слов, путём замены в них одних букв на другие согласно заложенным в алгоритмы правилам.