Что такое нулевой коллинеарный вектор
Что такое вектор
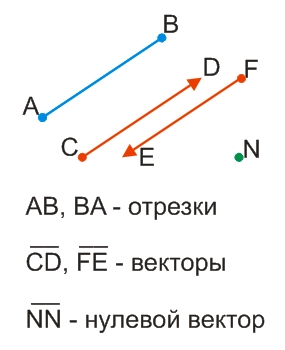
Направленный отрезок называется вектором.
Отрезок называется направленным, если у него указаны начало и конец, т.е., указано направление.
О том, что данный отрезок является вектором, говорит горизонтальная черта над буквами, обозначающими вектор.
Условия равенства векторов:
Длиной вектора или модулем вектора называется длина отрезка, обозначающего этот вектор.
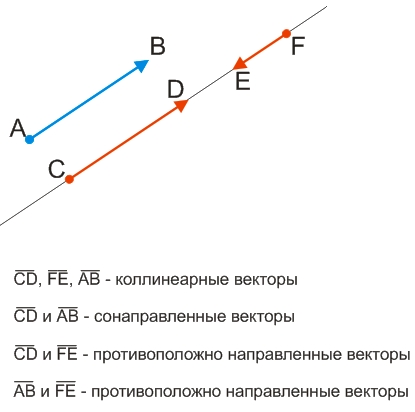
Коллинеарными называются вектора, лежащие на одной и той же прямой или принадлежащие параллельным прямым.
Нулевой вектор считается коллинеарным любому вектору.
Два ненулевых коллинеарных вектора считаются сонаправленными, если их направления совпадают.
Нулевой вектор считается сонаправленным любому вектору.
Два ненулевых коллинеарных вектора считаются противоположно направленными, если их направления противоположны.
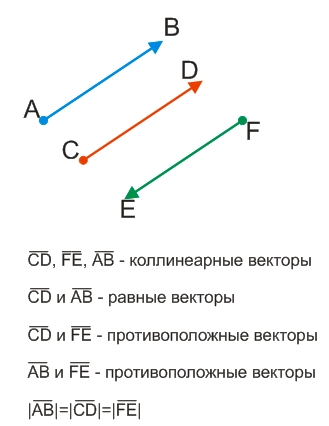
Два сонаправленных вектора считаются равными, если они имеют одинаковую длину (модуль).
Два противоположно направленных вектора, имеющих одинаковые модули, называются противоположными (следует различать противоположно направленные векторы и противоположные векторы).
Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:
Код кнопки: 
Политика конфиденциальности Об авторе
Что такое нулевой коллинеарный вектор
1. Основные определения
Вектор представляет собой направленный отрезок прямой, для которого определены правила (законы) сложения с другими векторами, правило вычитания векторов, правило умножения вектора на число, скалярное произведение двух векторов и некоторые другие операции.
Число, выражающее длину направленного отрезка, называют модулем вектора и обозначают той же буквой, что и сам вектор, но без стрелки наверху, например: модулем вектора `vec v` является число `v`. Часто для обозначения модуля вектора прибегают к помощи знака абсолютной величины и пишут, например, `|vec v|` или `|vec F|`.
Вектор называется нулевым, если его начало и конец совпадают. Нулевой вектор не имеет определённого направления и его длина (модуль) равна нулю.
Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Так, например, на рис. 3 векторы `vec a`, `vec b` и `vec c` коллинеарны.
Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление.
В физике точка приложения вектора иногда имеет принципиальное значение. Достаточно вспомнить рычаг: две равные по модулю силы, направленные в одну и ту же сторону, производят на рычаг разное действие, если плечи сил не равны друг другу. И всё же сами силы равны друг другу! Бывают и случаи, когда вектору трудно приписать конкретную точку приложения. Например, если одна система отсчёта движется относительно другой со скоростью `vec v`, то какой точке приписать эту скорость? Всем точкам движущейся системы!
2. Сложение двух векторов.
Пусть даны два произвольных вектора `vec a` и `vec b` (рис. 5а).
Описанное правило есть просто определение суммы векторов. Как и в случае с числами, сумма векторов не зависит от порядка слагаемых, и поэтому можно записать
Оба способа сложения дают идентичный результат и одинаково часто применяются на практике. Когда речь идёт о нахождении суммы трёх и более векторов, часто последовательно используют правило треугольника. Поясним сказанное.
3. Сложение трёх и более векторов.
Пусть нужно сложить три вектора `vec a`, `vec b` и `vec d` (рис. 6).
Для этого по правилу треугольника сначала находится сумма любых двух векторов, например `vec a` и `vec b`, потом полученный вектор `vec c = vec a + vec b` по тому же правилу складывается с третьим вектором `vec d`. Тогда полученный вектор `vec f = vec c + vec d` и будет представлять собой сумму трёх векторов `vec a`, `vec b` и `vec d`: `vec f = vec a + vec b + vec d`. Как и в случае с двумя векторами, порядок слагаемых не влияет на конечный результат.
Так, на рис. 7 вектор `vec g` представляет собой сумму векторов `vec a`, `vec b`, `vec d`, `vec e`, найденную по правилу многоугольника: `vec g = vec a + vec b + vec d + vec e`.
Не всякая векторная сумма может иметь физический смысл. Не всякие величины вообще имеет смысл складывать. Так, например, бессмысленно говорить, что, если у меня температура `36,6^@` и у вас тоже `36,6^@`, то вместе у нас температура `73,2^@`, хотя складывать температуры (числа) никто не запрещает. Всё же чаще всего сумма температур представляет собой никому не нужную величину; она редко входит в какие-либо уравнения (входит почти случайно).
Иное дело – с массой. Если система состоит из тел с массами `m_1`, `m_2`, `m_3` и т. д., то масса всей системы равна `m = m_1 + m_2 + m_3 + ` и т. д. (Если на лифте написано, что максимальный груз, перевозимый лифтом, равен `500` кг, то перед входом в лифт нужно убедиться, что сумма масс вносимых в лифт грузов не превышает `500` кг.) Говорят, что масса – есть аддитивная величина (от английского слова add – добавлять, прибавлять, складывать). А вот температура – не аддитивная величина.
В последнем равенстве мы встречаемся с умножением вектора на скаляр. Поясним эту процедуру.
4. Умножение вектора на скаляр.
Произведением вектора `vec a` на число `k` называют новый вектор `vec b = k vec a`, коллинеарный вектору `vec a`, направленный в ту же сторону, что и вектор `vec a`, если `k > 0`, и в противоположную сторону, если `k
Коллинеарность векторов, условия коллинеарности векторов.
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).
 |
| рис. 1 |
Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Доказательство третего условия коллинеарности
Пусть есть два коллинеарные вектора a = < ax ; ay ; az > и b = < nax ; nay ; naz >. Найдем их векторное произведение
Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:
| ax | = | ay | . |
| bx | by |
| Вектора a и b коллинеарны т.к. | 1 | = | 2 | . |
| 4 | 8 |
| Вектора a и с не коллинеарны т.к. | 1 | ≠ | 2 | . |
| 5 | 9 |
| Вектора с и b не коллинеарны т.к. | 5 | ≠ | 9 | . |
| 4 | 8 |
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | . |
| bx | by |
Решим это уравнение:
Ответ: вектора a и b коллинеарны при n = 6.
Примеры задач на коллинеарность векторов в пространстве
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:
| ax | = | ay | = | az | . |
| bx | by | bz |
Вектора a и b коллинеарны т.к. 1 4 = 2 8 = 3 12
Вектора a и с не коллинеарны т.к. 1 5 = 2 10 ≠ 3 12
Вектора с и b не коллинеарны т.к. 5 4 = 10 8 ≠ 12 12
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | = | az | . |
| bx | by | bz |
Из этого соотношения получим два уравнения:
| 3 | = | 2 |
| 9 | n |
| 3 | = | m |
| 9 | 12 |
Решим эти уравнения:
| n = | 2 · 9 | = 6 |
| 3 |
| m = | 3 · 12 | = 4 |
| 9 |
Ответ: вектора a и b коллинеарны при n = 6 и m = 4.
Условие коллинеарности векторов
В статье ниже рассмотрим условия, при которых векторы считаются коллинеарными, а также разберем тему на конкретных примерах. И, прежде чем приступить к обсуждению, напомним некоторые определения.
Коллинеарные векторы – ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому.
Данное определение дает возможность убедиться в коллинеарности векторов в их геометрическом отображении, однако точность такого способа может иметь погрешности, например, в зависимости, от качества самого чертежа. Поэтому обратимся к алгебраическому толкованию: сформируем условие, которое будет явным признаком коллинеарности.
Координатная форма условия коллинеарности векторов
Мы можем также получить еще одно условие коллинеарности векторов, опираясь на понятие их произведения.
Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
Рассмотрим применение условия коллинеарности на конкретных примерах.
Решение
Ответ: заданные векторы коллинеарны.
Решение
Решение
Согласно выведенному выше условию, векторы коллинеарны, если
b → = λ · a → ⇔ b x = λ · a x b y = λ · a y ⇔ p = λ · 2 3 = λ · 7
Ответ: при p = 6 7 заданные векторы коллинеарны.
Также распространены задачи на нахождения вектора, коллинеарного заданному. Решаются они без затруднений, основываясь на условии коллинеарности: : достаточным будет взять произвольное действительное число λ и определить вектор, коллинеарный данному.
Решение
Решение
Определение вектора
В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.
Для начала дадим определение:
Вектор – это направленный отрезок прямой.
Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.
Нулевой вектор
Под нулевым вектором 0 → будем понимать любую точку плоскости или пространства.
Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.
Длина вектора
Под длиной вектора A B → понимается число, большее либо равное 0, и равное длине отрезка АВ.
Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.
Коллинеарность векторов
Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.
Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.
Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.
Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.
Направление векторов
Считается, что нулевой вектор является сонаправленым к любым другим векторам.
Равные и противоположные векторы
Равными называются сонаправленные вектора, у которых длины равны.
Противопожными называются противоположно направленные вектора, у которых их длины равны.
Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.
Углы между векторами
Угол φ = ∠ A O B называется углом между векторами a → = O A → и b → = O B → .
Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.
Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π 2 радиан).