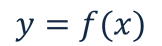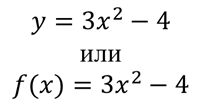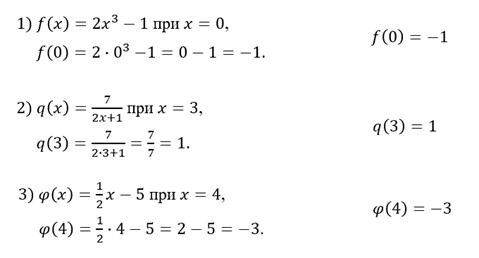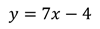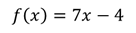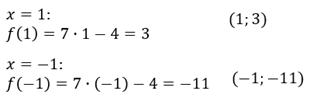Что такое область значения
Общая информация
У каждой функции y = f (x) есть два типа переменных: зависимые и независимые. Переменная «х» является независимой, поскольку она может принимать любые значения, кроме тех, которые «превращают» функцию в пустое множество (этого необходимо избегать). Они бывают с одной или несколькими независимыми переменными. Необходимо выяснить все значения зависимой переменной.
Существует несколько методов решения задач такого типа. К ним относятся следующие способы: автоматизированный и ручной. Решение первым подразумевает использование специальных программных оболочек и web-приложений, позволяющих найти область значения функции. Онлайн-калькулятор с решением применяется для тех, кто выполняет большое количество вычислений или проверку вычислений.
В различных дисциплинах необходимо исследовать поведение функций. Например, при проектировании какого-либо программного продукта. Программисты занимаются поиском «багов», при которых происходит некорректная работа приложения. Если заданы недопустимые параметры независимой переменной, то произойдет ошибка. Это называется исключением, и его всегда следует обрабатывать. При проектировании различных устройств нужно также уметь находить область значения функции.
Основные понятия
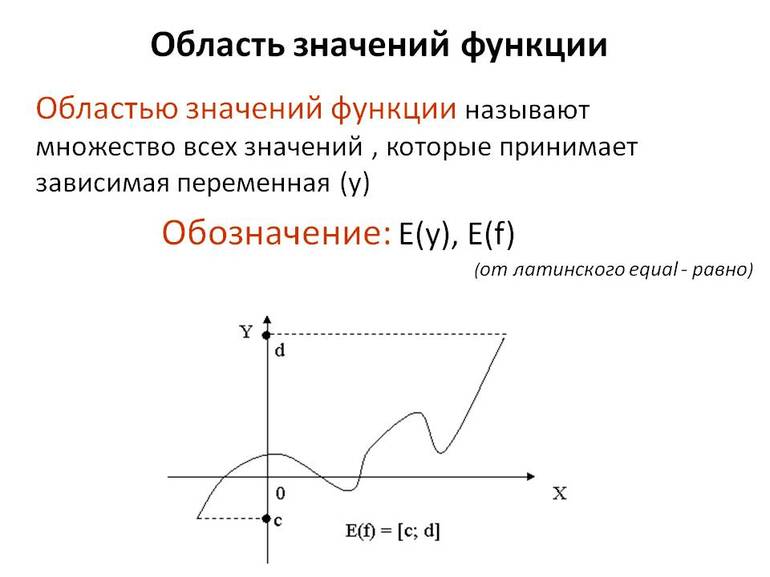
Руководствуясь некоторыми данными, можно сделать вывод: областью значений некоторой функции называются все ее допустимые значения. Обозначается она буквой «E», т. е. E (f) или E (y). Когда y = f (x) является сложной (w = f (x, y, z)), тогда можно ее обозначить «E (w)».
Независимая переменная, принимающая некоторые значения, называется аргументом. Для конкретного случая существует определенный алгоритм. Можно сразу определить E (f), но в некоторых ситуациях нужно выполнить некоторые преобразования.
Специалисты-математики утверждают, что важным аспектом является определение типа функции. Следовательно, следует разобраться в их классификации. Для этого необходимо знать их графики и названия.
Типы функций
Перед тем, как найти все допустимые значения, нужно знать область значения некоторых элементарных функций. Для каждой из них существует свой промежуток:
Если функция является многочленом четной степени, то для нее существует интервал [m;+бесконечность). Значение «m» — наименьшее значение многочлена. На промежутке (-бесконечность;n) число n — наибольшее его значение.
Довольно сложной задачей считается нахождение области значений тригонометрических функций. Примером одной из них считается y = cos (2x) + 2cos (x). Кроме того, при нахождении E (f) необходимо руководствоваться не только табличными значениями. Этих данных мало, поскольку нужно также знать о свойствах некоторых функций и способы нахождения E.
Важные свойства
Для качественного исследования нужно знать свойства простых функций: монотонность, непрерывность, дифференцируемость, четность или нечетность, периодичность, область определения и значения. Среди свойств можно выделить несколько основных:
Последние два свойства применяются для непрерывных функций. Простое решение позволяет получить первое свойство. При этом очень важно доказать ее монотонность. Задача существенно упрощается, когда удается доказать четность или нечетность функции, а также ее периодичность. По необходимости следует проверять и использовать некоторые ее свойства: непрерывность (при разрыве нужно определить его точку или интервал), монотонность, дифференцируемость, периодичность, четность или нечетность и т. д.
Методы нахождения
Существует много способов нахождения области значений. Однако для решения задач нужно подбирать оптимальный метод, поскольку следует избегать лишних вычислений. Например, если функция является простой, то нет необходимости применять сложные алгоритмы решения. К методам нахождения относятся следующие:
Для каждого из методов существует определенный алгоритм. Хотя встречаются случаи, когда целесообразно применить два простых метода. Нужно руководствоваться минимальным количеством вычислений и затраченным временем.
Для каждого элемента
Иногда в задачах следует найти E (f) при условии, когда функция является сложной. Очень распространенная методика разбиения задачи на подзадачи, которая применяется не только в дисциплинах с физико-математическим уклоном, но в экономике, бизнесе и других направлениях. Решение с помощью метода последовательного нахождения E (f) каждой из функций. Алгоритм имеет такой вид:
Однако довольно сложно ориентировать по данному алгоритму, поскольку нужно разобрать решение примера с его помощью. Дана функция y = log0.5 (4 — 2 * 3^x — 9^x). Решается задача таким образом:
Необходимо обратить внимание на пункты 1, 3 и 5. Они являются очень важными, поскольку от них зависит правильность решения. Очень важно уметь анализировать полученную функцию в 4 пункте.
Оценочный способ
Еще одним методом определения E (f) является способ оценки. Необходимо оценить непрерывную функцию в нижнем и верхнем направлениях. Еще следует доказать достижение нижней и верхней границ. Для этой цели существует также алгоритм. Он немного проще предыдущего. Суть его заключается в следующем:
Необходимо разобрать алгоритм на примере функции y = cos (7x) + 5 * cos (x). Следует учитывать, что известен только один знак неравенства. Второй нужно доказать оценочным методом. Решение задачи имеет такой вид:
Производная, min и max
Одним из простейших способов нахождения E (f) является взятие производной функции. Этот метод можно комбинировать с определением максимального и минимального значений. Математики рекомендуют простейший алгоритм:
Практическое применение алгоритма — решение задачи этим методом. Например, нужно найти E (arcsin (x)). Решение выполняется по нескольким этапам:
В некоторых случаях рекомендуется вычислять пределы, поскольку часть задач решается только с их применением. Существует определенный тип задач, в которых нужно доказать, что отрезок является E (f) конкретной функции. Например, следует выяснить принадлежность [-1;1] функции sin (x). Для этого необходимо воспользоваться вышеописанным алгоритмом:
Отрезок [-1;1] является E (sin (x)). Оптимальный метод — нахождение производной и определение E (f). В этом примере необходимо знать и проверить периодичность.
Таким образом, существует несколько способов нахождения E (f), но всегда необходимо выбирать метод, приводящий к минимуму вычислений. Нет смысла усложнять решение, поскольку большинство алгоритмов направлены на оптимизацию вычислений.
Область значений функции (множество значений функции). Необходимые понятия и примеры нахождения
Зачастую в рамках решения задач нам приходится искать множество значений функции на области определения или отрезке. Например, это нужно делать при решении разных типов неравенств, оценках выражений и др.
В рамках этого материала мы расскажем, что из себя представляет область значений функции, приведем основные методы, которыми ее можно вычислить, и разберем задачи различной степени сложности. Для наглядности отдельные положения проиллюстрированы графиками. Прочитав эту статью, вы получите исчерпывающее представление об области значений функции.
Начнем с базовых определений.
Обратите внимание, что понятие множества значений функции не всегда тождественно области ее значений. Эти понятия будут равнозначны только в том случае, если интервал значений x при нахождении множества значений совпадет с областью определения функции.
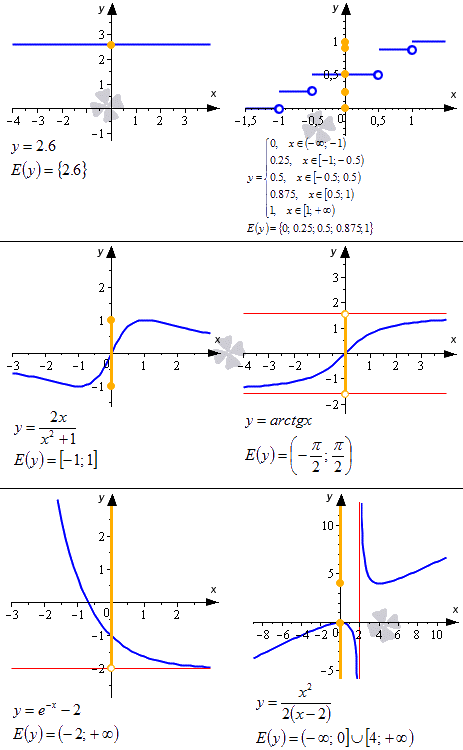
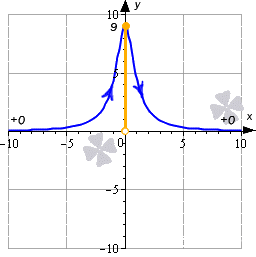
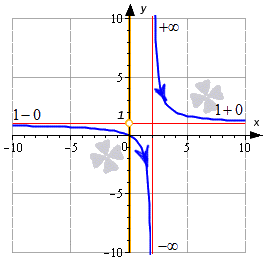
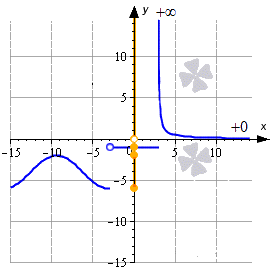
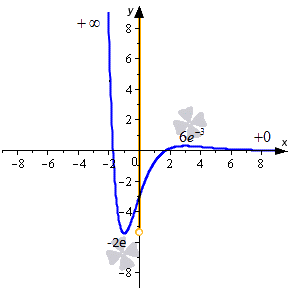
Ниже приводится иллюстрация, на которой показаны некоторые примеры. Синие линии – это графики функций, красные – асимптоты, рыжие точки и линии на оси ординат – это области значений функции.
Рассмотрим основные способы нахождения области значений функции.
Возьмем задачу, в которой нужно определить область значений арксинуса.
Решение
Решение
Все, что нам нужно сделать, – это вычислить наибольшее и наименьшее значение функции в заданном интервале.
Для определения точек экстремума надо произвести следующие вычисления:
Начнем с определения наибольшей и наименьшей точки, а также промежутков возрастания и убывания на заданном интервале. После этого нам нужно будет вычислить односторонние пределы в концах интервала и/или пределы на бесконечности. Иными словами, нам надо определить поведении функции в заданных условиях. Для этого у нас есть все необходимые данные.
Решение
Определяем наибольшее и наименьшее значение функции на заданном отрезке
Решение
Решение
Мы получили, что значения функции будут возрастать от минус бесконечности до плюс бесконечности при изменении значений x от нуля до плюс бесконечности. Значит, множество всех действительных чисел – это и есть область значений функции натурального логарифма.
Ответ: множество всех действительных чисел – область значений функции натурального логарифма.
Решение
Данная функция является определенной при условии, что x – действительное число. Вычислим наибольшие и наименьшие значения функции, а также промежутки ее возрастания и убывания:
Посмотрим, как же ведет себя функция на бесконечности:
Из записи видно, что значения функции в этом случае будут асимптотически приближаться к 0.
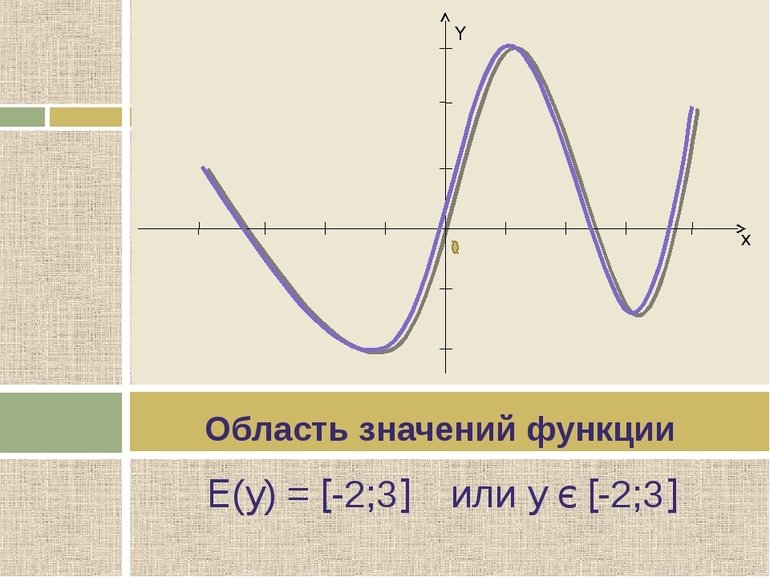
На нем видно, что областью значений функции будет интервал E ( y ) = ( 0 ; 9 ]
Ответ: E ( y ) = ( 0 ; 9 ]
А как быть в случае, если область определения некоторой функции представляет из себя объединение нескольких промежутков? Тогда нам надо вычислить множества значений на каждом из этих промежутков и объединить их.
Решение
Для открытого луча 2 ; + ∞ производим точно такие же действия. Функция на нем также является убывающей:
Это можно увидеть на графике:
Особый случай – периодические функции. Их область значения совпадает с множеством значений на том промежутке, который отвечает периоду этой функции.
Решение
Синус относится к периодической функции, а его период составляет 2 пи. Берем отрезок 0 ; 2 π и смотрим, каким будет множество значений на нем.
Если вам нужно знать области значений таких функций, как степенная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая, то советуем вам перечитать статью об основных элементарных функциях. Теория, которую мы приводим здесь, позволяет проверить указанные там значения. Их желательно выучить, поскольку они часто требуются при решении задач. Если вы знаете области значений основных функций, то легко сможете находить области функций, которые получены из элементарных с помощью геометрического преобразования.
Решение
Еще один пример запишем без пояснений, т.к. он полностью аналогичен предыдущему.
Решение
Теперь разберем, как найти область значений функции, которая не является непрерывной. Для этого нам надо разбить всю область на промежутки и найти множества значений на каждом из них, после чего объединить то, что получилось. Чтобы лучше понять это, советуем повторить основные виды точек разрыва функции.
Решение
Решение показано на графике:
Решение
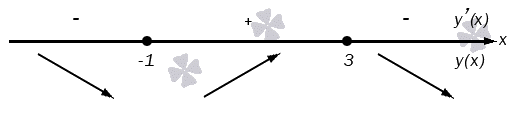
Она определена для всех значений аргумента, представляющих собой действительные числа. Определим, в каких промежутках данная функция будет возрастать, а в каких убывать:
Теперь найдем соответствующие значения функции:
Посмотрим на поведение функции на бесконечности:
Для вычисления второго предела было использовано правило Лопиталя. Изобразим ход нашего решения на графике.
Определение числовой функции. Область определения функции. Область значения функции.
Что такое область определения функции? что такое область значения функции? Давайте, в этой статье разберемся в понятиях числовой функции и ее характеристиках и свойствах.
Определение функции.
Функция y=f(x) — это когда каждому допустимому значению переменной x соответствует единственное значение переменной y или другими словами такая зависимость переменной y от переменной x.
х — называется независимой переменной или аргументом.
y – называется зависимой переменной или значением функции.
Множество чисел, где x∈X или D(f) — называется областью определения функции. Это множество всех допустимых значений переменной х.
Область значений функций, когда задаем правило или функцию, которая позволяет по произвольно выбранному значению x∈D(f) вычислить соответствующее значение y.
Переменную х или аргумент мы придумываем сами и подставляем в правило, которое задали или функцию. Далее рассчитываем переменную y или значение функции.
В тех диапазонах в которых существует переменная х называется областью определения функции.
В тех диапазонах в которых существует переменная y называется областью значения функции.
Графиком функции y=f(x), x∈X называется множество точек (x; f(x)) координатной плоскости.
Разберём пример №1:
Найдите область определения и область значения числовой функции y=x 2
Вместо переменной x мы можем брать любые числа и просчитать переменную y.
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 |
По графику также видно, что сколько бы угодно мы не проводили линий через ось х, мы найдем пересечение с графиком.
А теперь рассмотрим переменную у. В таблице мы видим, что переменная y принимает положительные значение, так как и самое минимальное значение 0. Следовательно, y∈[0; +∞).
Если посмотрим на график, то увидим, что графика ниже нуля нет. Следовательно, область значения функции E(f) = [0; +∞).
Разберём пример №2:
Найдите область определения и область значения числовой функции y=x+1?
Вместо переменной x мы можем брать любые числа и просчитать переменную y.
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
По графику также видно, что сколько бы угодно мы не проводили линий через ось х, мы найдем пересечение с графиком.

Рассмотрим переменную у. В таблице мы видим, что переменная y также принимает значения как в положительном, так и в отрицательном направлении. Следовательно, ограничений у переменной y нет, y∈(−∞; +∞). Область значения функции E(f) = (−∞; +∞).
Область значений
В данной статье приведено общее определение математической функции. В средних школах и на нематематических специальностях высших учебных заведениях изучают более простое понятие числовой функции, являющееся частным случаем математической функции.
Содержание
Определения
Обозначения
Связанные определения
Свойства
Свойства прообразов и образов
Классы функций
Вариации и обобщения
Функции нескольких аргументов
Определение функции легко обобщить на случай функции многих аргументов.
Примечания
См. также
Литература
Полезное
Смотреть что такое «Область значений» в других словарях:
область значений — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN codomain … Справочник технического переводчика
Область значений функции — Область значений функции множество значений, которые принимает функция в результате ее применения. Содержание 1 Определение 2 Примеры 2.1 Числовые функции … Википедия
область значений влияющих величин — Множество значений влияющих величин при изменении отдельной влияющей величины в установленных пределах. [ГОСТ Р 51317.4.30 2008 (МЭК 61000 4 30:2008)] EN range of influence quantities range of values of a single influence quantity [IEC 61000 4 30 … Справочник технического переводчика
область значений влияющих величин — 3.25 область значений влияющих величин (range of influence quantities): Множество значений влияющих величин при изменении отдельной влияющей величины в установленных пределах. Источник … Словарь-справочник терминов нормативно-технической документации
нормальная область значений влияющей величины — нормальная область Область значений влияющей величины, в пределах которой изменением результата измерений под ее воздействием можно пренебречь в соответствии с установленными нормами точности. Пример. Нормальная область значений температуры при… … Справочник технического переводчика
рабочая область значений (влияющей величины) — Область значений влияющей величины, в пределах которой нормируют дополнительную погрешность или показание средства измерений (ОСТ 45.159 2000.1 Термины и определения (Минсвязи России)). [http://www.iks… … Справочник технического переводчика
Нормальное значение [нормальная область значений] (влияющей величины) — 1. Значение [область значений] влияющей величины, устанавливаемое [ая] в стандартах или технической документации на средства измерений, при котором [в пределах которых] погрешности этих средств измерений не должны выходить за установленные… … Телекоммуникационный словарь
Рабочая область значений (влияющей величины) — 1. Область значений влияющей величины, в пределах которой нормируют дополнительную погрешность или показание средства измерений Употребляется в документе: ОСТ 45.159 2000 Отраслевая система обеспечения единства измерений. Термины и определения … Телекоммуникационный словарь
рабочая область значений влияющих величин — vardinės veikimo sąlygos statusas T sritis Standartizacija ir metrologija apibrėžtis Naudojimo sąlygos, kuriomis matavimo priemonės nurodytosios metrologinės charakteristikos patenka į apibrėžtas ribas. atitikmenys: angl. rated operating… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Функция. Область определения и область значений функции
Урок 1. Алгебра 9 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Функция. Область определения и область значений функции»
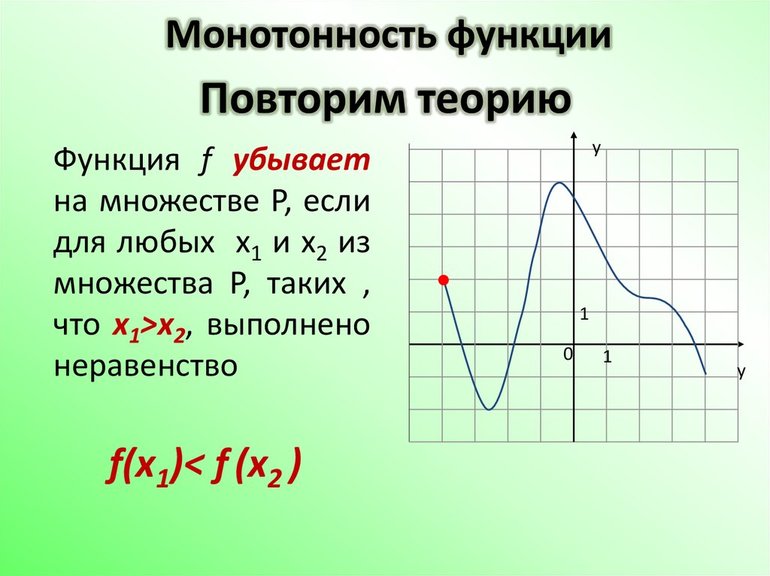
Зависимость переменной y от переменной x, при которой каждому значению переменной x соответствует единственное значение y, называют функцией.
В определении сказано, что только та зависимость является функцией, у которой каждому значению аргумента соответствует единственное значение функции.
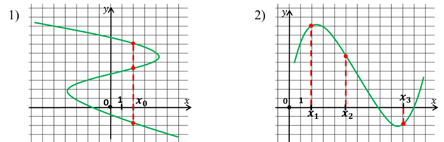
Рассмотрим первый график. Видим, что одному значению x может соответствовать несколько значений y. Значит, данная зависимость не является функцией.
Обратимся ко второму случаю. Какие бы значения аргумента мы не брали, каждому из них соответствует только одно значение функции. Можно сказать, что эта зависимость является функцией.
В общем виде любую функцию можно записать так:
Понятно, что функция может принимать различные значения в зависимости от значения аргумента. Найдём значение каждой функции при заданном значении аргумента.
Вы заметили, что в этом задании функции названы разными буквами. Действительно, функцию можно называть любой буквой латинского алфавита.
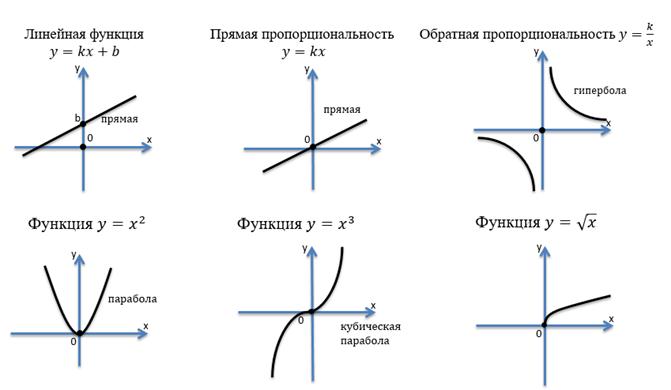
Ранее вами были изучены несколько важных функций. Вспомним их.
Сейчас попробуем выяснить, как же получается график функции, и дадим определение этому понятию.
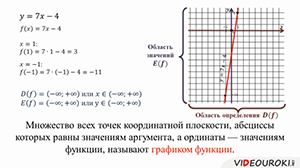
Можно записать её в таком виде:
Это линейная функция, графиком как вы помните, является прямая. Для изображения прямой достаточно двух точек.
Получаем точки с координатами (1;3) и (-1;-11).
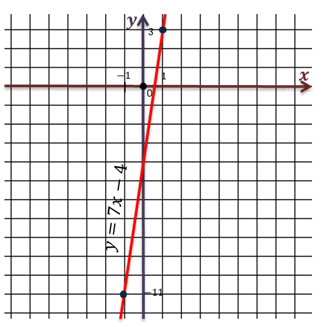
Проведём прямую через полученные точки.
Мы изобразили график функции.
Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — значениям функции, называют графиком функции.
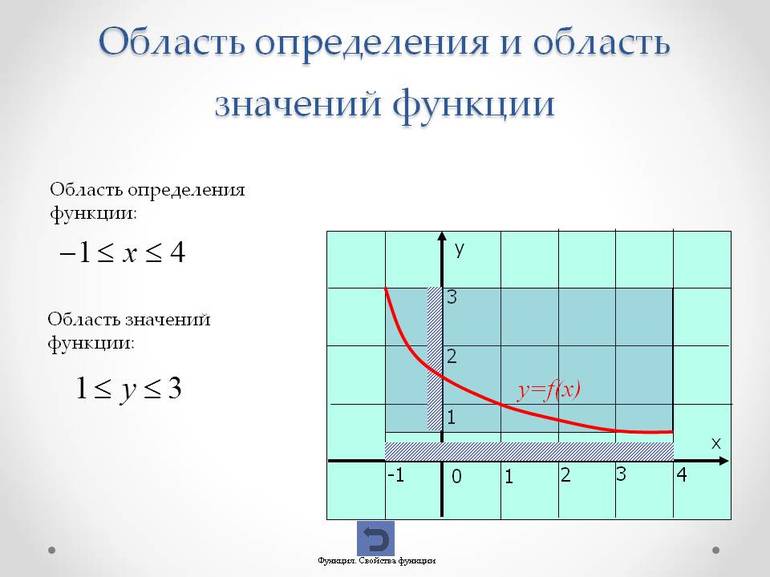
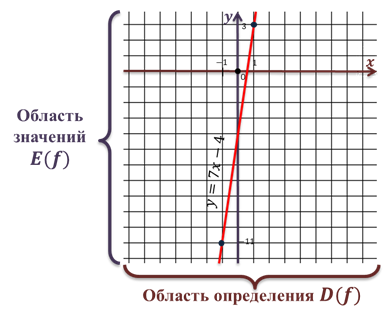
Все значения аргумента, т.е. переменной x образуют область определения функции, а все значения зависимой переменной, т.е. y, — область значений функции.
В данном случае x и y могут быть любыми числами, т.е. областью определения и областью значений является множество всех действительных чисел.
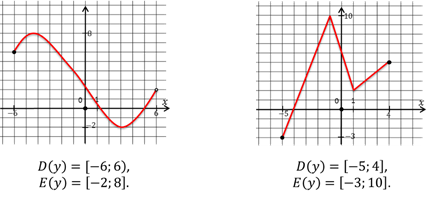
Потренируемся находить область определения и область значений функции по её графику.
Область определения можно находить не только по графику функции, но и по формуле, с помощью которой задана функция.