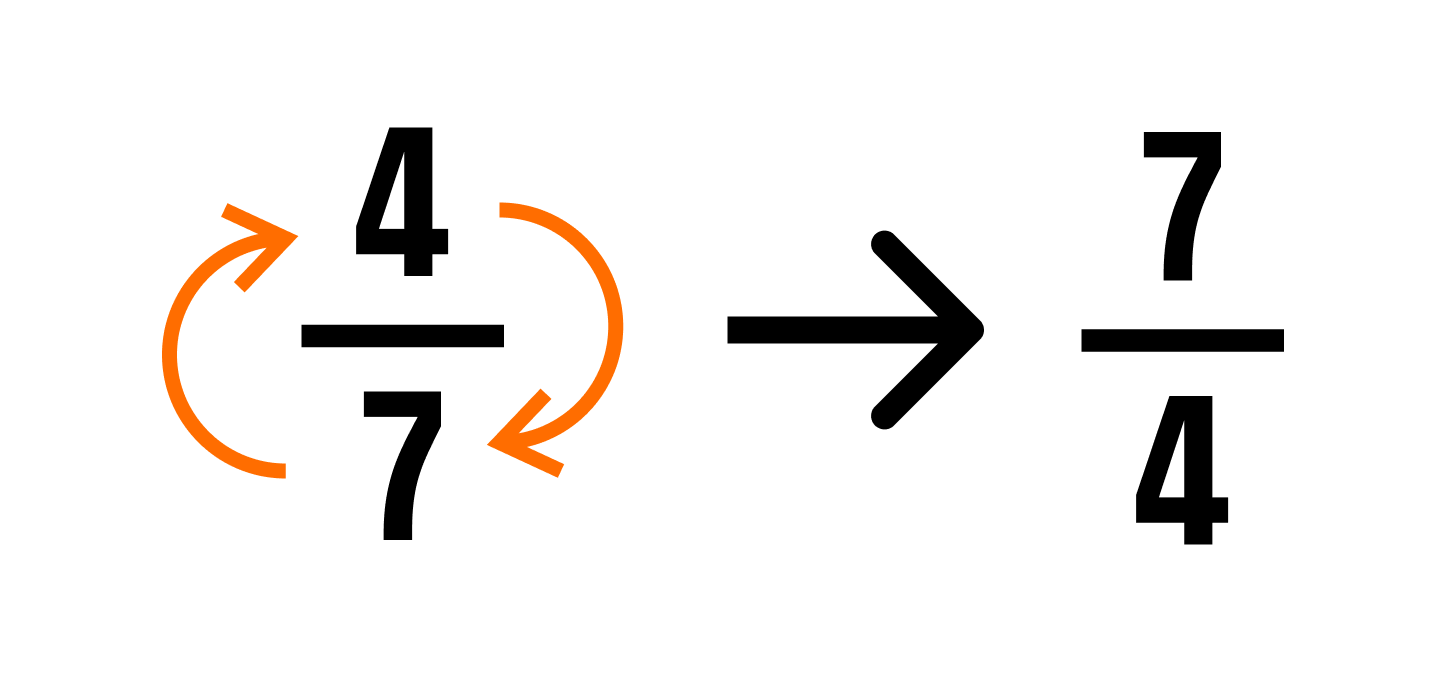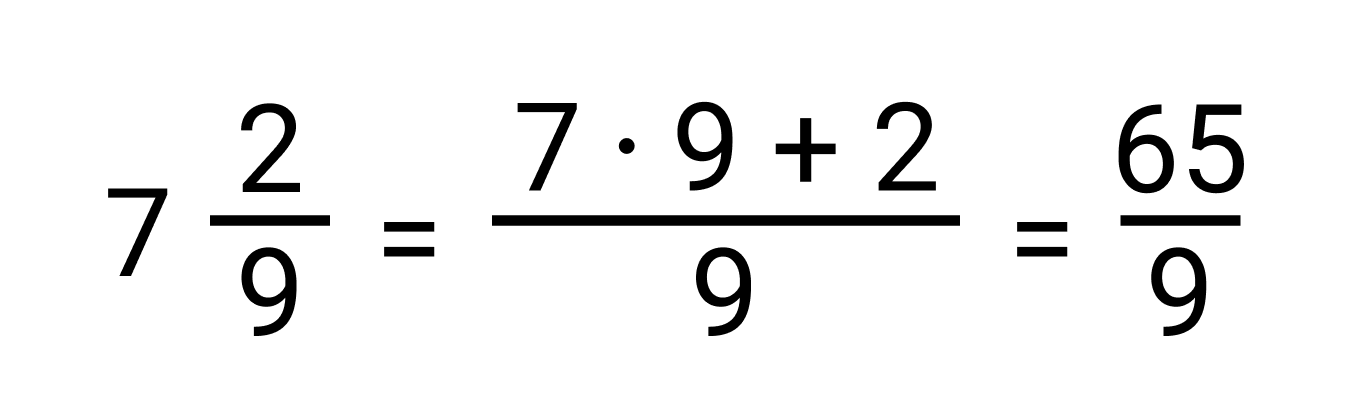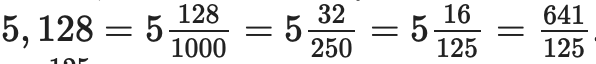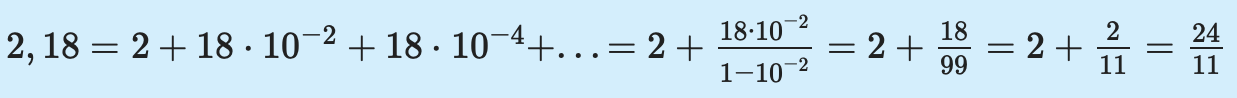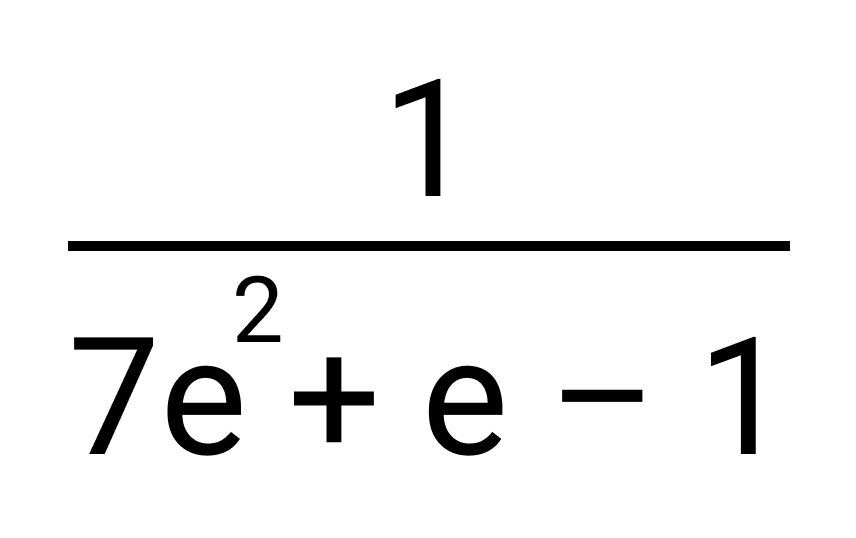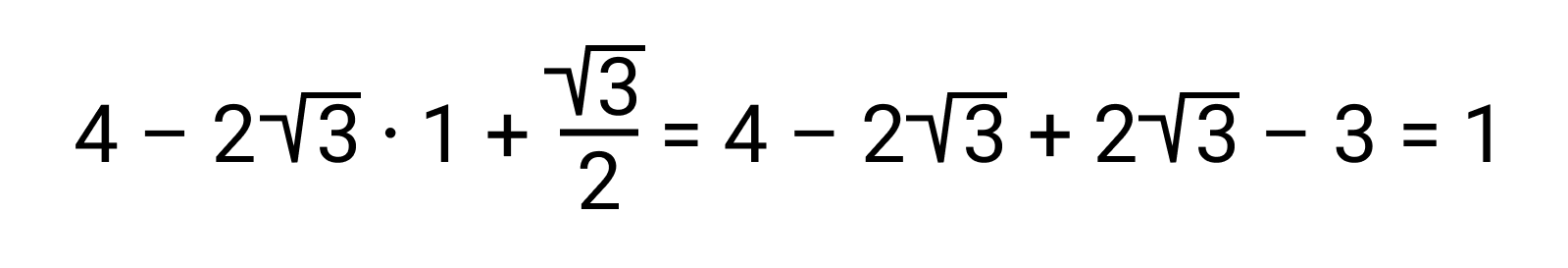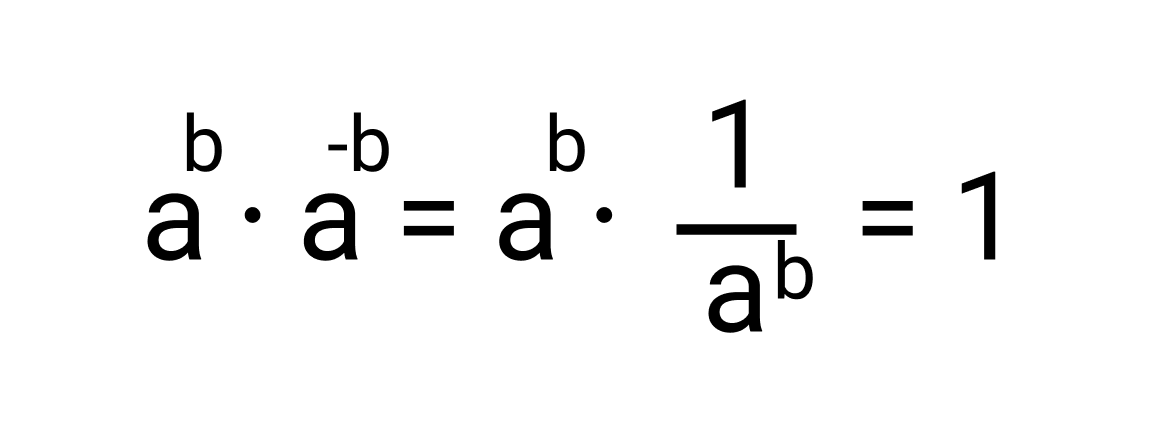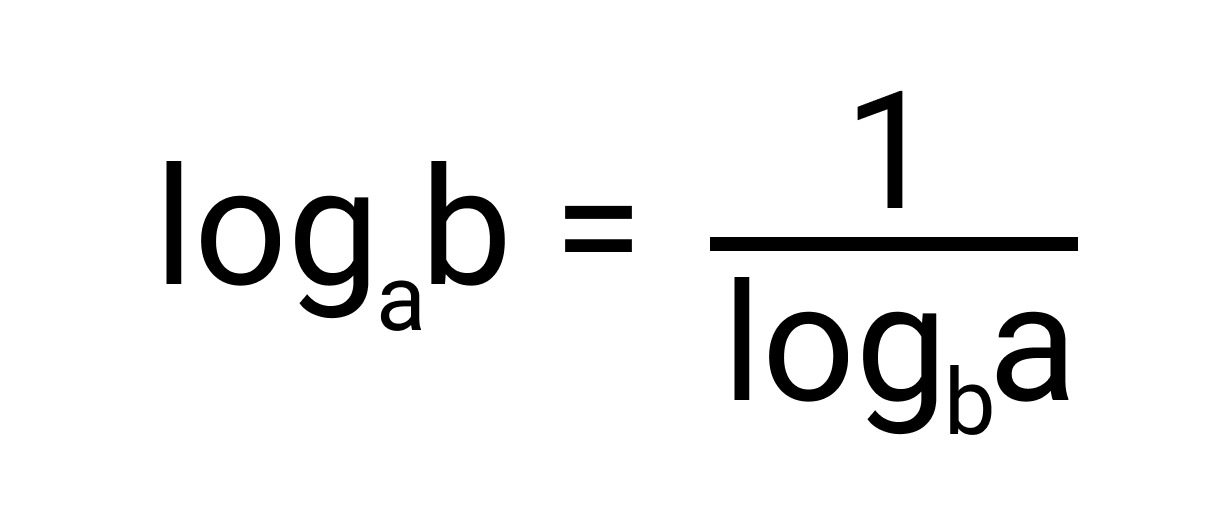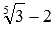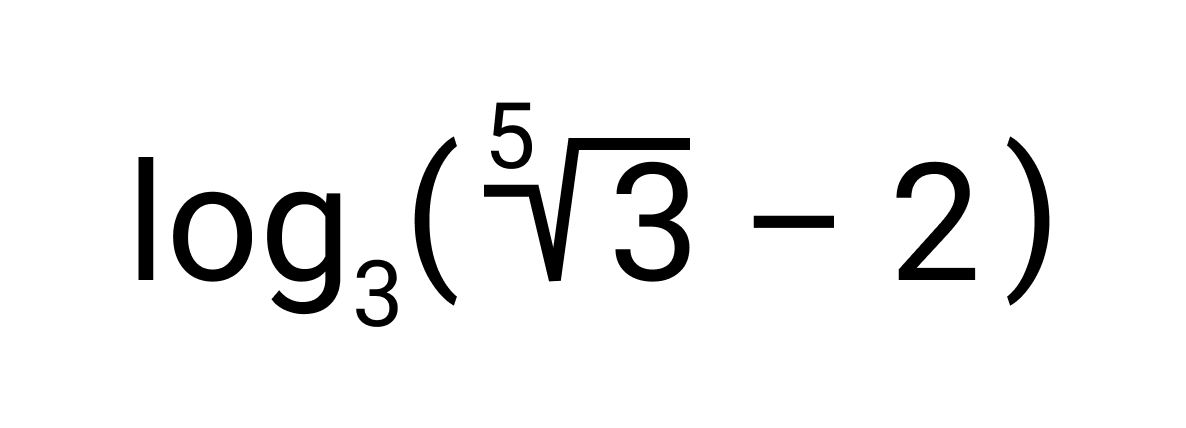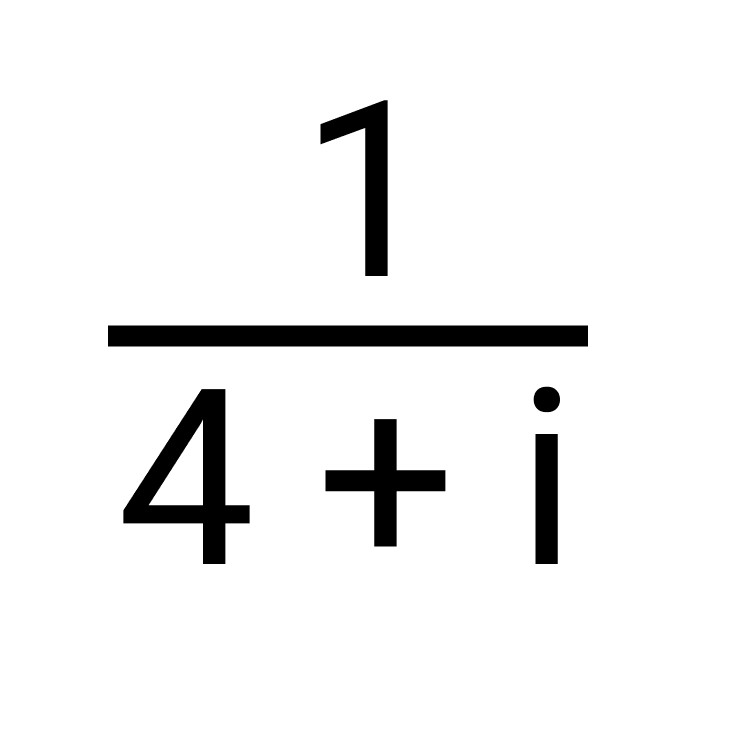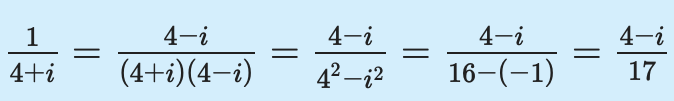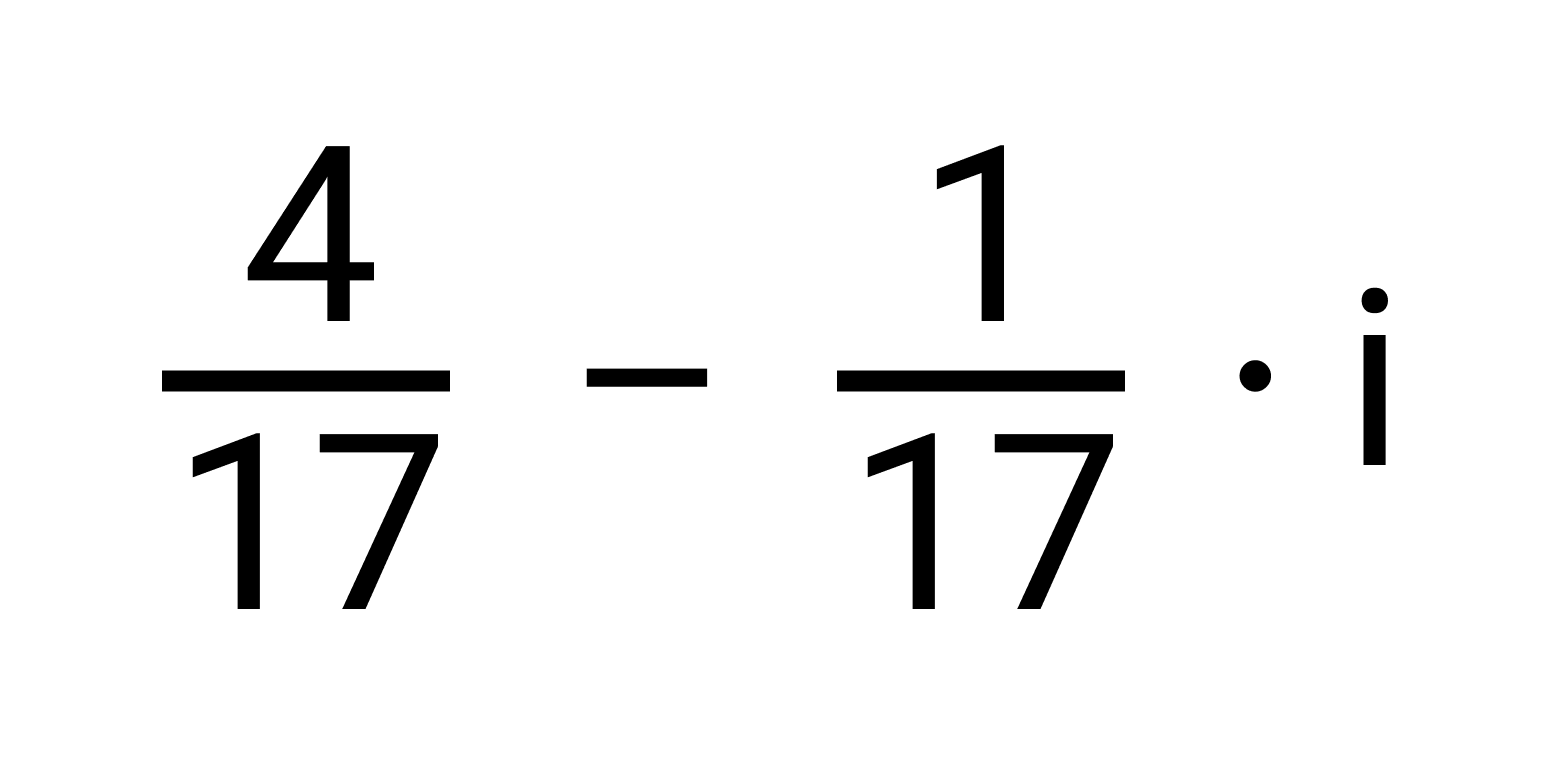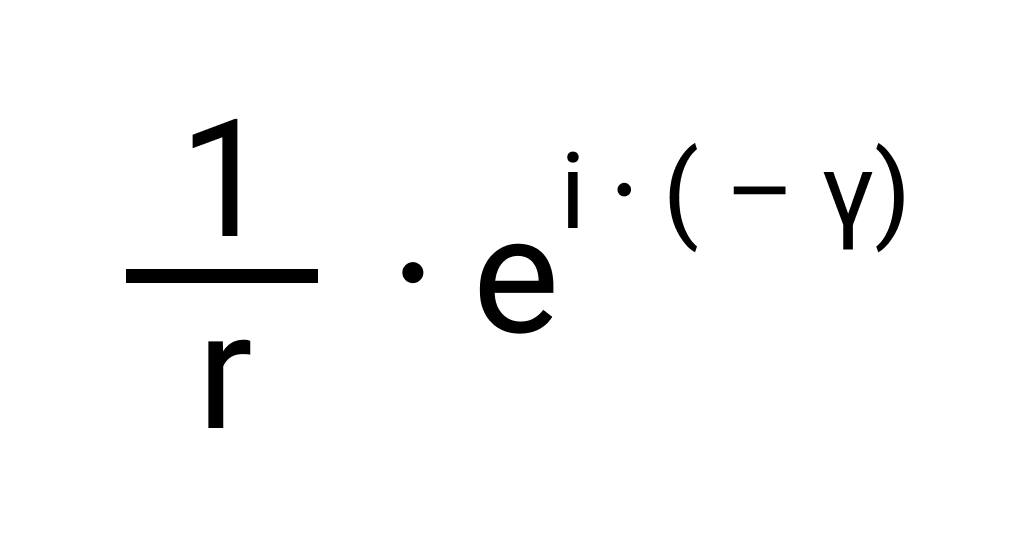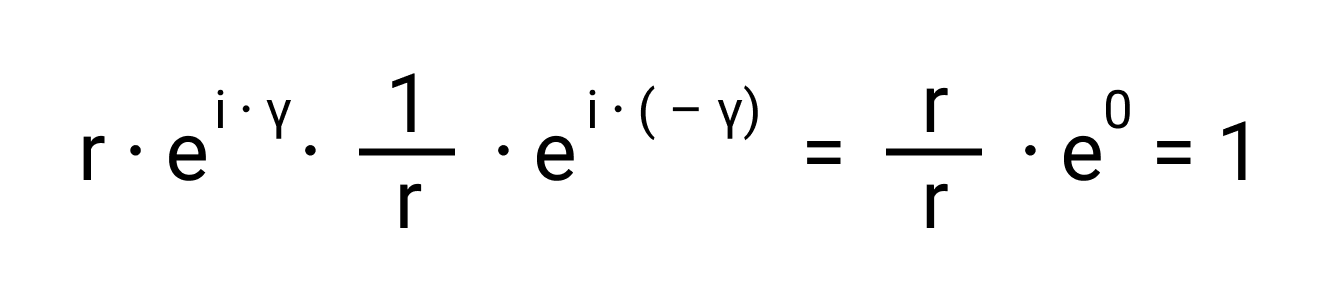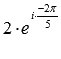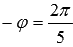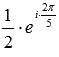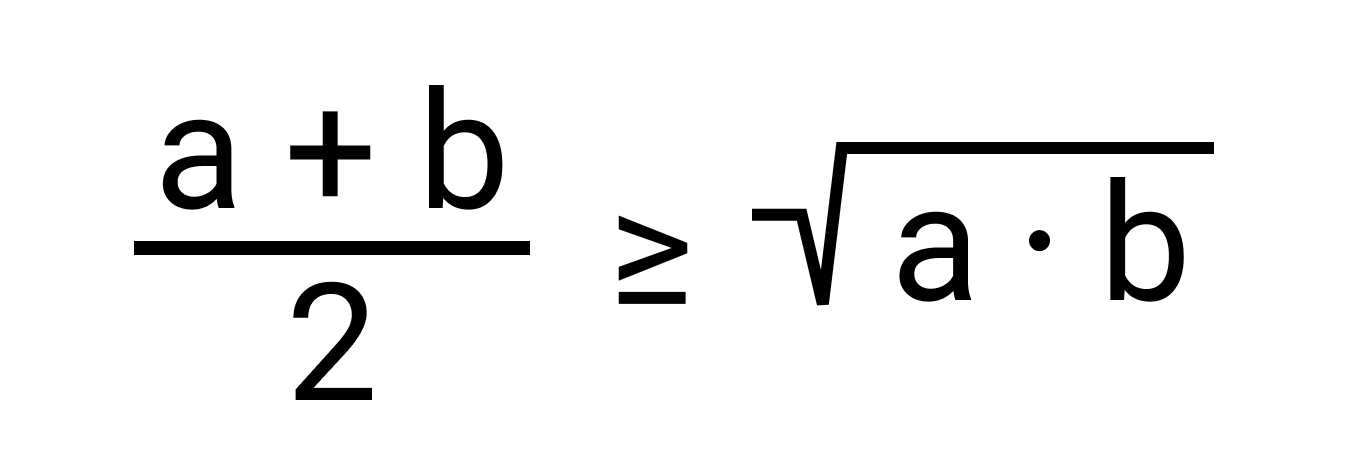Что такое обратное отношение в математике 6 класс

Источник

Урок 23 Бесплатно Прямая и обратная пропорциональные зависимости

Прямая и обратная пропорциональность

Давайте сначала разберемся, что такое пропорциональность.

Зависимость величин друг от друга может быть прямой и обратной.

Отношение между величинами описываются прямой или обратной пропорциональностью.

Прямая пропорциональность выражается так: \(\mathbf\)

Обратная пропорциональность выражается так: \(\mathbf>\)

x и y величины, зависящие друг от друга.

Пример

Если постоянно значение произведения, то множители зависят друг от друга обратно пропорционально.

По формуле видно, что площадь квадрата зависит от длины (ширины) его стороны, а длина стороны (ширина) зависит от его площади.

Какова эта зависимость, сейчас и рассмотрим.

Зависимость площади прямоугольника от длины при постоянном значении ширины является прямо пропорциональной зависимостью этих величин.

Зависимость площади прямоугольника от ширины при постоянном значении длины является прямо пропорциональной зависимостью этих величин.

Пусть одна клетка равна 1 см. Рассмотрим рисунок:

Ширина прямоугольника b постоянная величина

b = 4 см

a₁ = 6 см

a₂ = 7 см

Найдем площади прямоугольников S₁ и S₂

\(\mathbf = a_ <1>\cdot b = 6 \cdot 4 = 24>\) см 2

\(\mathbf = a_ <2>\cdot b = 7 \cdot 4 = 28>\) см 2

Вывод: при увеличении стороны прямоугольника увеличилась площадь прямоугольника.

Рассмотрим другой вариант зависимости

Зависимость одной из сторон прямоугольника от второй стороны при постоянном значении площади прямоугольника является обратно пропорциональной зависимостью. Пусть одна клетка равна 1 см

Площадь прямоугольника S постоянная величина

S = 24 см 2

b₁ = 4 см

Увеличим высоту прямоугольника- сторону прямоугольника b₁ на 2 см_, получим

b₂ = 6 см

Найдем ширину прямоугольника- сторону a₂

Вывод: при увеличении одной стороны прямоугольника и постоянном значении площади, вторая сторона уменьшается.

Таким образом, мы подошли к основным понятиям пропорциональной зависимости. Чтобы было легко разобраться в несложных схемах ниже, мы дадим пояснение символам:

1) Две величины прямо пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, так же увеличивается (уменьшается) в n количество раз.

2) Две величины обратно пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, уменьшается (увеличивается) в n количество раз.

Примеров прямой и обратной пропорциональности множество.

Однако не все величины зависят друг от друга прямо пропорционально или обратно пропорционально, встречаются и более простые и более сложные зависимости величин.

Надо понимать, что даже если какие-нибудь две величины возрастают или убывают, то между ними не обязательно существует пропорциональная зависимость.

Например, с течением времени увеличивается возраст человека и его размер ноги, но эти величины не являются пропорциональными, так как при удвоении возраста размер ноги человека не удваивается

Пройти тест и получить оценку можно после входа или регистрации

Error: /home/l/ladle/public_html/system/cache/templates_c/7bd86af47e89f3f45217921246f856cf.php does not exists!

Примеры решения задач на прямую и обратную зависимость

Рассмотрим некоторые варианты задач на пропорциональную зависимость, в которых величины зависят прямо пропорционально одна от другой.

Задача 1

Для приготовления из 3 кг черной смородины по рецепту требуется 3,3 кг сахара.

Сколько сахара потребуется для приготовления варенья из 5 кг черной смородины?

Решение:

Пусть х (кг) сахара потребуется для приготовления варенья из 5 кг ягод.

Составим краткую запись задачи в виде таблицы:

Определим, как зависят масса сахара и масса ягод.

Чем больше ягод, тем больше нужно сахара, следовательно, между величинами прямо пропорциональная зависимость.

В таблице вертикальными стрелками изображаем прямо пропорциональную зависимость величин.

Так как зависимость величин прямо пропорциональная, составим пропорцию в точном соответствии с таблицей.

Отношение значений одной величины равно отношению соответствующих значений другой величины.

Составим уравнение, используя основное свойство пропорции:

\(\mathbf < = <5,5>>\) (кг) сахара потребуется для приготовления варенья из 5 кг ягод.

Ответ: \(\mathbf < = <5,5>>\) (кг)

Задача 2

Автомобиль, двигаясь с постоянной скоростью, проехал 400 км за 5 часов.

За какое время автомобиль проедет 600 км?

Решение:

Пусть х (ч) – время, за которое автомобиль проедет 600 км.

Составим краткую запись задачи в виде таблицы:

Так как движение происходит с постоянной скоростью, то \(\mathbf < = \cdot>\).

Чем больше расстояние, тем больше требуется времени для преодоления этого расстояния, значит, зависимость между величинами S и t прямо пропорциональная.

Изображаем в таблице краткой записи задачи вертикальными стрелками прямо пропорциональную зависимость величин.

Так как зависимость величин прямо пропорциональная, составим пропорцию в точном соответствии с таблицей.

Отношение значений одной величины равно отношению соответствующих значений другой величины.

Составим уравнение, используя основное свойство пропорции:

\(\mathbf < = <7,5>>\) (ч) время, за которое автомобиль проедет 600 км

Ответ: \(\mathbf < = <7,5>>\) (ч)

Примеры решения задач, в которых величины зависят обратно пропорционально одна от другой.

Задача 1

Для перевозки гравия потребовалось 42 машины грузоподъемностью 5 т.

Сколько нужно машин грузоподъемностью 7 т, чтобы перевезти тот же объем гравия?

Решение:

Краткую запись задачи оформим в виде таблицы:

Определим, как зависят величины друг от друга.

Чем больше грузоподъемность машины, тем меньше машин потребуется для перевозки груза.

Получаем обратно пропорциональную зависимость.

Изображаем на краткой записи задачи вертикальными стрелками, направленными в разные стороны, обратно пропорциональную зависимость величин.

При обратно пропорциональной зависимости отношение значений одной величины будет равно обратному отношению соответствующих значений другой величины.

А это значит, что при составлении пропорции одно из отношений получится перевернутым.

Составим уравнение, используя основное свойство пропорции:

\(\mathbf < = <30>>\) (шт.) машин грузоподъёмностью 7 т понадобится для перевозки гравия.

Ответ: \(\mathbf < = <30>>\) (шт.)

Задача 2

Велосипедист проехал путь от дачи до дома за час со скоростью 10 км/ч. Сколько понадобится времени велосипедисту на преодоление этого пути со скоростью 20 км/ч?

Решение:

Пусть х (ч) время велосипедиста, если он будет двигаться со скоростью 20 км/ч. Составим краткую запись задачи в виде таблицы:

Определим, как зависят V и t, где V— скорость движения велосипедиста, t— время движения.

Чем больше скорость велосипедиста, тем меньше времени ему потребуется для преодоления пути.

Получаем обратно пропорциональную зависимость величин друг от друга.

Изображаем на краткой записи задачи вертикальными стрелками, направленными в разные стороны, обратно пропорциональную зависимость величин.

При обратно пропорциональной зависимости отношение значений одной величины будет равно обратному отношению соответствующих значений другой величины.

А это значит, при составлении пропорции одно из отношений получаем перевернутым.

Составим уравнение, используя основное свойство пропорции:

\(\mathbf < = <0,5>>\) (ч) время велосипедиста, если он будет двигаться со скоростью 20 км/ч.

Ответ: \(\mathbf < = <0,5>>\) (ч)

У меня есть дополнительная информация к этой части урока!

Рассмотрим некоторые, часто встречающиеся, варианты прямой и обратной пропорциональной зависимости величин в решении задач

Примеры задач, в которых величины зависят прямо пропорционально одна от другой.

Величины, зависящие друг от друга

Величина постоянная

Величина дроби и ее числитель

Объем выполненной работы и затраченное время

Производительность труда и объем выполненной работы

Длина пути и время прохождения этого пути

Пройденный путь и скорость движения

Количество товара и стоимость

Длина (ширина) прямоугольника и его площадь

Примеры задач, в которых величины зависят обратно пропорционально одна от другой

Знаменатель дроби и значение дроби

Число рабочих и время выполнения ими заданной работы

Производительность всех рабочих

Производительность труда и время потраченное на работу

Скорость движения и время

Количество товара и его цена

Пройти тест и получить оценку можно после входа или регистрации

Заключительный тест

Пройти тест и получить оценку можно после входа или регистрации

Источник

Взаимно обратные числа

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение взаимно обратных чисел

С предыдущих уроков математики мы знаем: если прибавить или вычесть из числа нуль — оно не изменится. Точно также, если умножить или разделить число на единицу.

Ноль — нейтральный элемент для сложения и вычитания. При этом числа, которые в сумме дают ноль, называют противоположными.

Единица — нейтральный элемент для умножения и деления. Поэтому симметричными называют числа, чье произведение дает единицу.

Два числа называют взаимно обратными, если их произведение равно 1.

Обратное число к данному числу — это такое число, которое мы умножаем на данное число и получаем единицу.

Если числа a и b взаимно обратные, то можно сказать, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Также можно говорить, что числу a обратно число b, а числу b обратно число a.

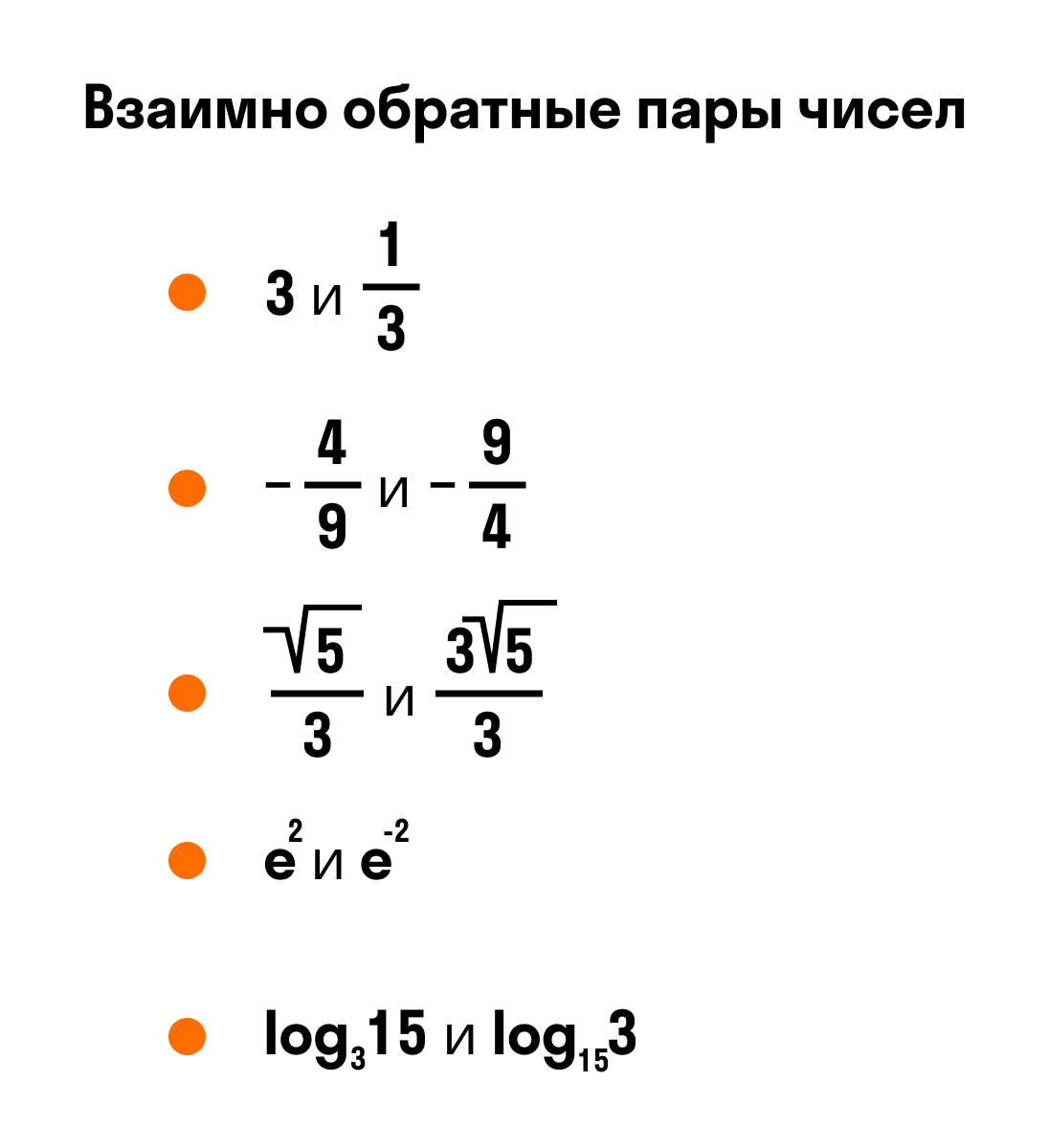
Приведем примеры взаимно обратных чисел. Так как произведение двух единиц равно 1, то по определению числа 1 и 1 — взаимно обратные.

Определение взаимно обратных чисел относится к любым числам — натуральным, целым, действительным, комплексным.

Как найти число, обратное данному числу

Иногда число, обратное данному числу, очевидно. Так бывает с натуральными числами и обыкновенными дробями. В других случаях приходится проводить вычисления. Например, с иррациональными и комплексными числами.

Рассмотрим каждый отдельный случай нахождения числа, обратного данному числу.

Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Число, обратное обыкновенной дроби

Числом, обратным обыкновенной дроби a/b, является дробь b/a.

Чтобы это проверить, выполним умножение обыкновенных дробей a/b и b/a — получим 1. Значит дроби a/b и b/a — взаимно обратные числа.

Если числитель и знаменатель дроби a/b поменять местами, то получится дробь b/a, обратная дроби a/b.

Это правило значительно экономит время. Можно сразу записать число, обратное данной обыкновенной дроби без каких-либо вычислений.

Число, обратное натуральному числу

Нахождение числа, обратного данному натуральному числу, можно свести к нахождению числа, обратного дроби. Для этого нужно записать натуральное число как дробь со знаменателем 1.

Пусть нам дано натуральное число n, и нужно записать число, обратное числу n. Так как натуральное число n равно дроби n/1, то, поменяв местами числитель и знаменатель этой дроби, получим дробь 1/n, которая и является числом, обратным натуральному числу n.

Итак, натуральному числу n обратным числом является число 1/n, то есть, дробь с числителем 1 и знаменателем n. Значит n и 1/n — взаимно обратные числа.

Отдельно отметим число, обратное натуральному числу 1. Число, обратное единице, это единица. Пара взаимно обратных чисел 1 и 1 уникальна тем, что составляющие ее числа равны, других таких пар взаимно обратных чисел не существует.

Найти число, обратное смешанному числу

Напомним, что смешанное число выглядит так: A b/c. Чтобы найти число, обратное смешанному числу, нужно представить данное смешанное число в виде неправильной дроби, а уже после найти число, обратное этой дроби. Как это работает рассмотрим на примере.

Пример

Найти число, обратное смешанному числу

Сначала выполним перевод смешанного числа в неправильную дробь:

Число, обратное дроби 65/9, есть дробь 9/65. Поэтому, смешанному числу 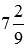обратно число 9/65.

Ответ: 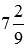и 9/65 взаимно обратные числа.

Найти число, обратное десятичной дроби

Конечную десятичную дробь или периодическую десятичную дробь можно заменить обыкновенной дробью. Поэтому найти число, обратное конечной или периодической десятичной дроби, можно через поиск числа, которое обратно обыкновенной дроби. Разберемся на примерах.

Пример 1

Найти число, которое обратно десятичной дроби 5,128.

Переведем конечную десятичную дробь в обыкновенную:

Числом, обратным полученной дроби, является обыкновенная дробь 125/641. Это и есть решение задачи.

Пример 2

Какое число является обратным для периодической десятичной дроби 2,(18)?

Переведем периодическую десятичную дробь в обыкновенную:

Обратная дробь для 24/11 — 11/24. Значит, числом, обратным исходной десятичной дроби 2,(18), является дробь 11/24.

Так как бесконечным непериодическим десятичным дробям отвечают иррациональные числа, то числа, которые обратны им, также записывают в виде дробных выражений.

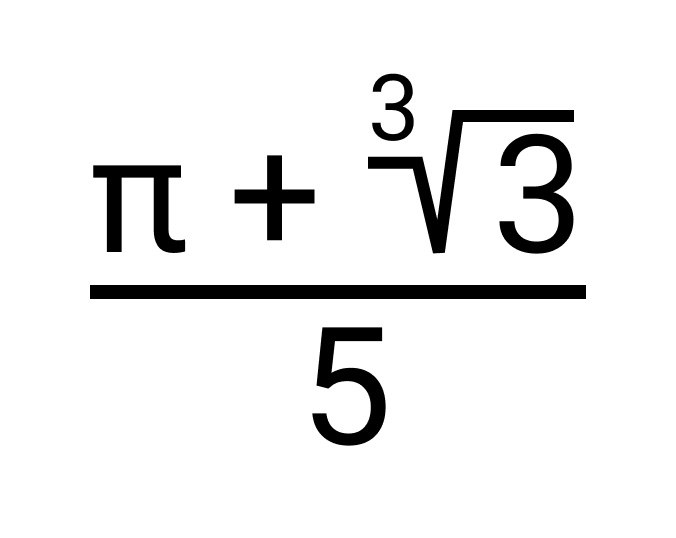
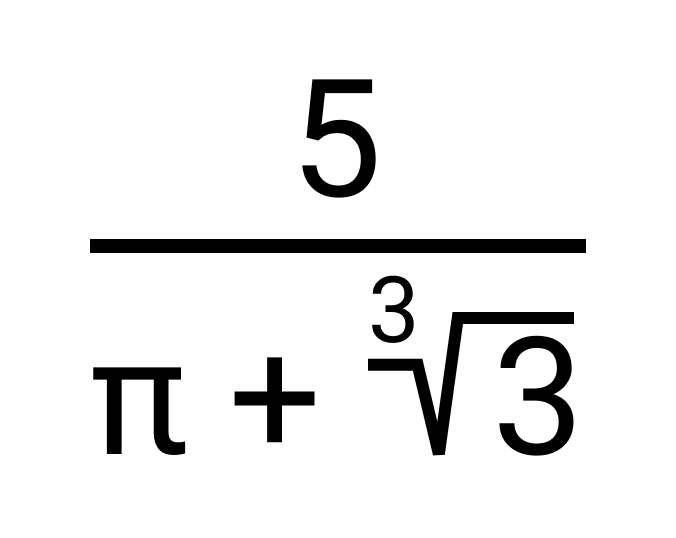
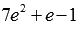
Например, иррациональному числу обратно число , а иррациональному числу обратно число

Взаимно обратные числа с корнями

Важно запомнить, что вид взаимно обратных чисел может отличаться от a и 1/a. Поэтому нужно быть внимательным. Особенно это касается чисел, записи которых содержат знак корня. Рассмотрим на примере, как это бывает.

Пример

Вычислим произведение этих чисел:

Так как в ответе мы получили единицу и мы знаем, что произведение взаимно обратных чисел равно 1, значит эти числа можно назвать взаимно обратными.

Ответ: да, число взаимно обратны.

Взаимно обратные числа со степенями

Допустим, есть число, которое равно какой-то степени числа a. То есть, число a возведено в степень b. Обратным числу ab будет число a-b. Проверим.

Пример

Взаимно обратные числа с логарифмами

У логарифма числа a по основанию b обратное число равно логарифму числа b по основанию a. То есть log _b a и log _a b — взаимно обратные числа.

Действительно, из свойств логарифма следует, что

, откуда log _b a * log _a b = 1.

Пример

Записать число, которое обратно логарифму числа 3 по основанию

Число, обратное числу 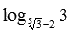, выглядит так:

Ответ:

Найти число, обратное комплексному числу

Сейчас узнаем, как находить число, обратное комплексному числу z.

Пример 1

Найти число, обратное комплексному числу 4 + i.

4 + i =

Умножим числитель и знаменатель полученного дробного выражения на число
4 + i.

Ответ:

или

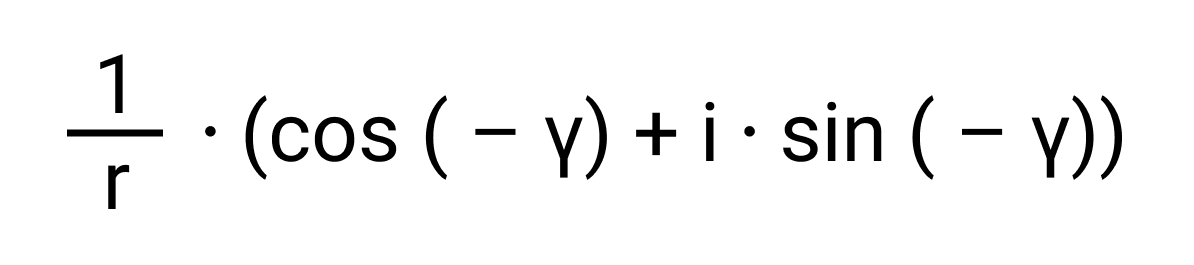
Действительно, и

Пример 2

Определить число, обратное комплексному числу

В этом примере r = 2 и 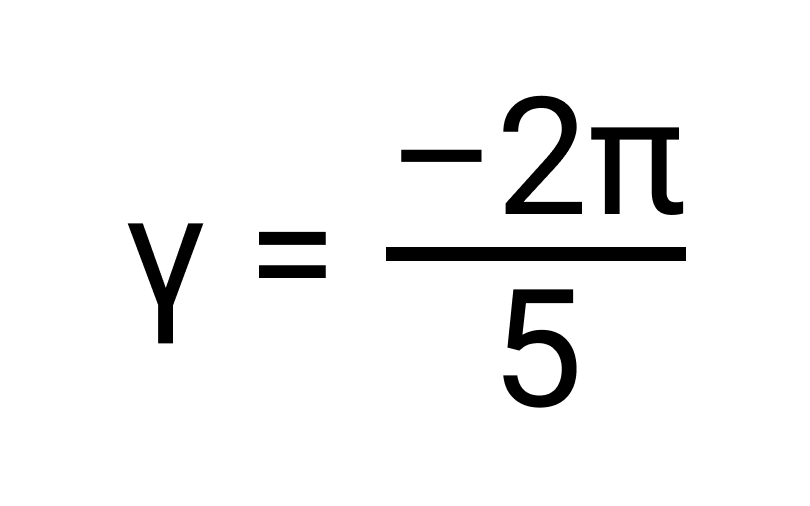, откуда 1/r = 1/2 и

Следовательно, нужное нам обратное число равно

Являются ли числа взаимно обратными? Да, мы только что это доказали.

Ответ:

Неравенство с суммой взаимно обратных чисел

В математике есть специальная теорема о сумме взаимно обратных чисел — давайте ее сформулируем и узнаем ключевое свойство.

Теорема

Сумма двух положительных взаимно обратных чисел больше или равна 2.

Доказательство теоремы:

Нам известно, что среднее арифметическое положительных чисел a и b всегда больше или равно среднему геометрическому этих чисел, то есть,

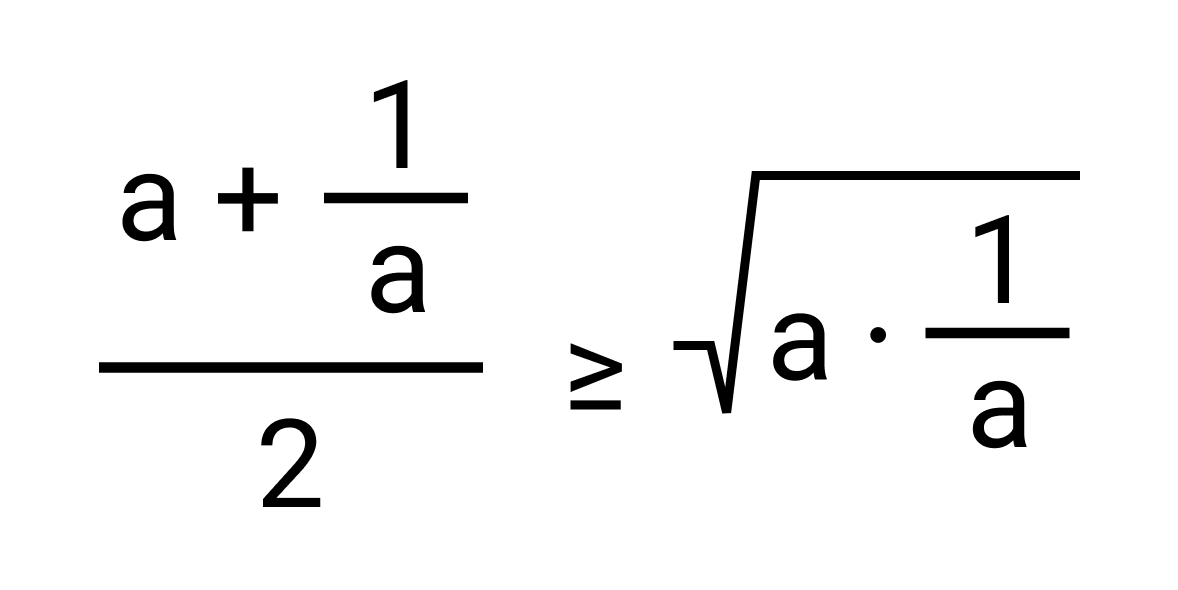
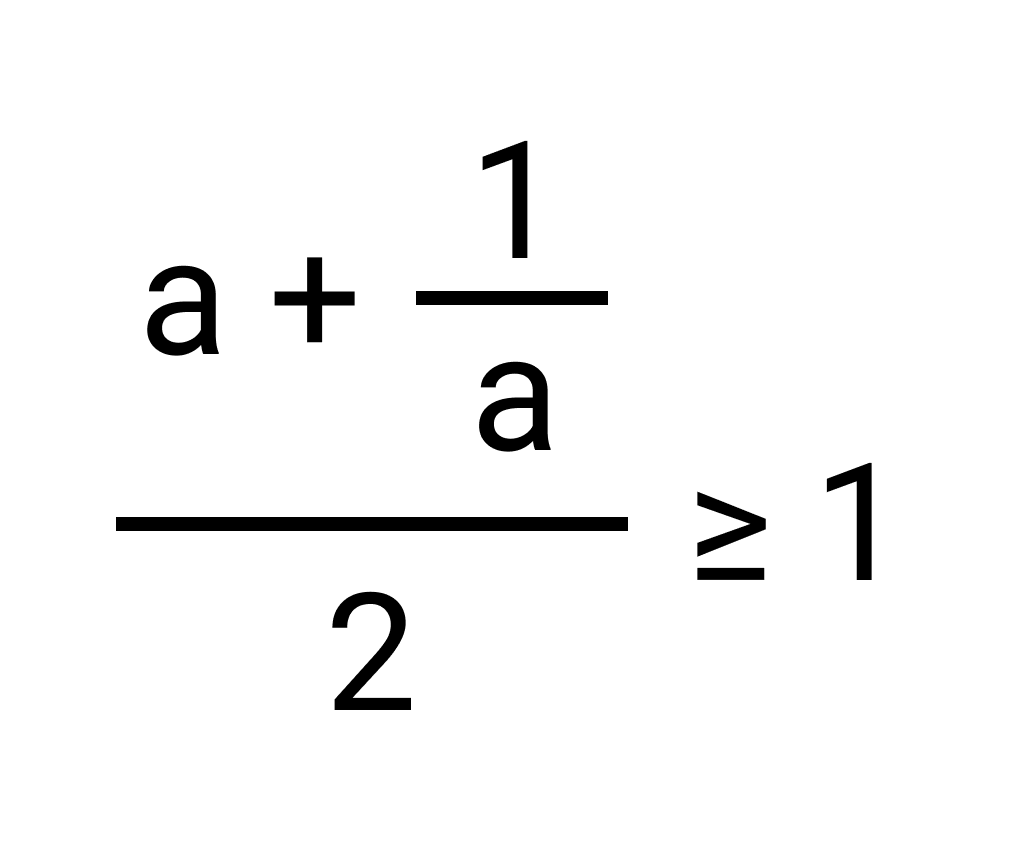
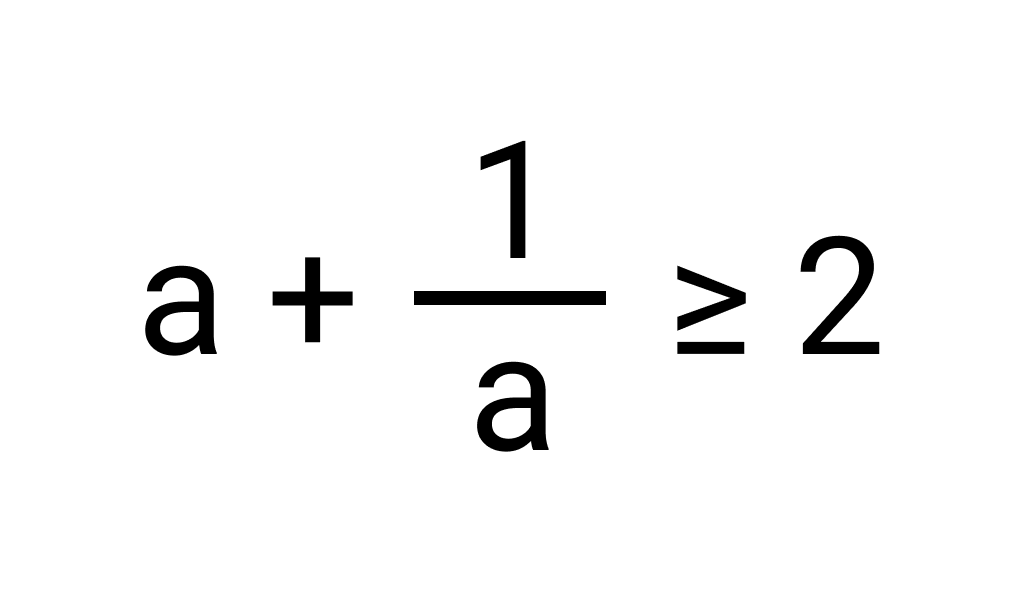
Если в качестве b мы возьмем число, обратное a, то полученное неравенство будет выглядеть так: откуда и , что и требовалось доказать.

Пример

Вычислить сумму взаимно обратных чисел 2/3 и 3/2,

Источник